SAT/SMT 튜토리얼
이 포스팅은 Coursera 강의, ‘Automated Reasoning: Satisfiablity‘의 SAT, SMT 튜토리얼입니다.
수업 자료 출처: https://www.coursera.org/learn/automated-reasoning-sat
일반 소개
이 강의에서는 만족 가능성(Satisfiability)이라는 개념과 SAT 해결이라는 기술에 대해 다룹니다. SAT 해결은 특정 공식이 만족 가능한지, 즉 참인지 거짓인지를 확인하는 문제를 해결하는 것을 의미합니다.
놀랍게도 추상적으로 느껴지는 이 기술은 스케줄링, 스도쿠 퍼즐 해결, 프로그램 정확성 검증 등 다양한 분야에서 활용됩니다. 더욱이 포스터 인쇄처럼 우리 주변에서 쉽게 접할 수 있는 문제에도 적용될 수 있다는 사실은 정말 흥미롭습니다.
강의에서 제공되는 퀴즈를 풀어보는 것은 물론, Z3와 같은 도구를 직접 활용하여 문제를 해결해 보는 경험을 통해 만족 가능성에 대한 이해를 더욱 높일 수 있습니다. 아래 링크는 Z3 solver를 파이썬에서 활용하는 방법을 소개하는 튜토리얼입니다.
SAT 소개
SAT 해결을 이해하기 전에, 핵심 개념인 명제 논리 공식에 대해 살펴보겠습니다.
명제 논리 공식은 불리안 변수와 논리 연산자로 구성됩니다. 논리 연산자에는 부정(negation), 논리합(disjunction), 논리곱(conjunction), 함의(implication), 동치(bi-implication) 등이 있습니다.
만족 가능성(Satisfiability)이란 명제 논리 공식이 참이 되도록 변수에 값을 할당할 수 있는지를 의미합니다. 만족 가능한 공식을 SAT(Satisfiable)이라고 부르며, 이를 만족시키는 변수 할당을 만족 할당(Satisfying Assignment)이라고 합니다.
쉽게 말해, SAT는 명제 논리 공식이 참이 될 수 있는 조건이 존재하는지 확인하는 문제입니다.
예시 01.
- 공식: $A\land B \lor \neg C$
- 만족 가능 여부: SAT
- 만족 할당: {A = True, B = True, C = True}
예시 02.
-
공식: $(p \lor q) \land (\neg p \lor \neg q) \land (p \lor \neg q)$
-
만족 가능 여부: SAT
-
만족 할당:
-
경우 1: {p = True, q = False}
-
경우 2: {p = False, q = True}
-
예시 03.
-
공식: $(p \lor q) \land (\neg p \lor \neg q) \land (p \land q)$
-
만족 가능 여부: Unsatisfiable
위의 여러 예시들을 통해 알 수 있듯이, SAT(Satisfiability) 문제는 주어진 논리식이 참이 되게 하는 변수 값의 조합이 존재하는지를 판별하는 문제입니다. 이 문제를 해결하는 한 가지 방법은 진리표(Truth Tables)를 작성하는 것입니다. 진리표를 사용하는 방법은 모든 가능한 변수 값의 조합을 살펴보면서, 그 중에서 주어진 논리식을 만족하는(satisfiable) 조합이 있는지를 찾아냅니다.
예시 01.
- 공식: $A\land B \lor \neg C$
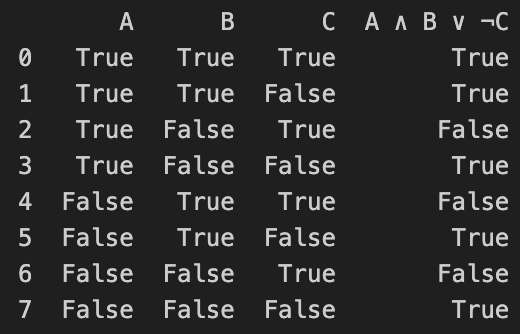
위 예시에서는 True, False로 진리표를 작성했는데요, 대개는 True를 1, False를 0으로 표현합니다.
예시 02.
- 공식: $\neg ((p \land q ) \rightarrow (p \lor r))$
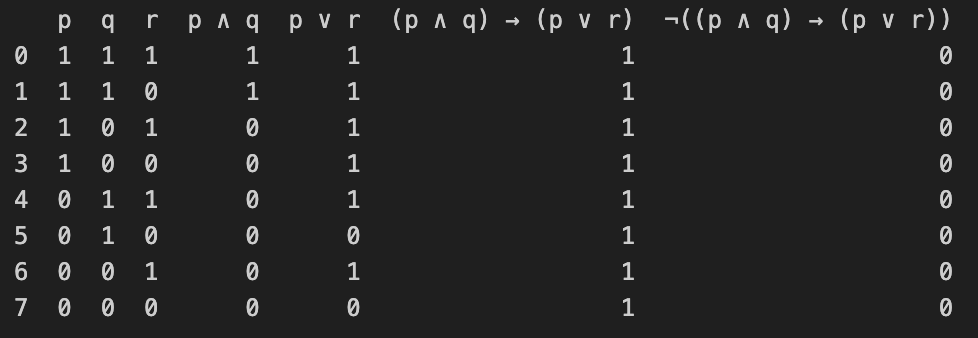
진리표를 사용하는 방식은 직관적이고 간단해 보일 수 있지만, 변수의 수가 증가함에 따라 그 복잡성은 기하급수적으로 증가합니다. 왜냐하면, 각 변수에 대해 참(true) 또는 거짓(false)의 두 가지 상태가 가능하기 때문에, n개의 변수가 있다면 우리는 $2^n$개의 다른 조합을 살펴봐야 합니다. 예를 들어, 변수가 3개인 경우에는 $2^3 = 8$개의 조합을 살펴봐야 하고, 변수가 10개인 경우에는 $2^{10} = 1024$개의 조합을 검토해야 합니다.
이 방법의 장점은 모든 가능한 조합을 검토하기 때문에, 만약 해결책이 존재한다면 반드시 찾을 수 있다는 것입니다. 하지만 단점도 분명합니다. 변수의 수가 많아질수록 필요한 계산량이 엄청나게 증가하여, 실제로 많은 변수를 가진 복잡한 문제에 적용하기에는 다소 비현실적인 방법입니다.
SAT 문제는 논리식의 만족 가능성을 판단하는 문제입니다. 하지만 이 문제는 NP-완전 문제로 분류되는데, 모든 공식에 대해 효율적인 알고리즘이 존재하지 않을 가능성이 높습니다.
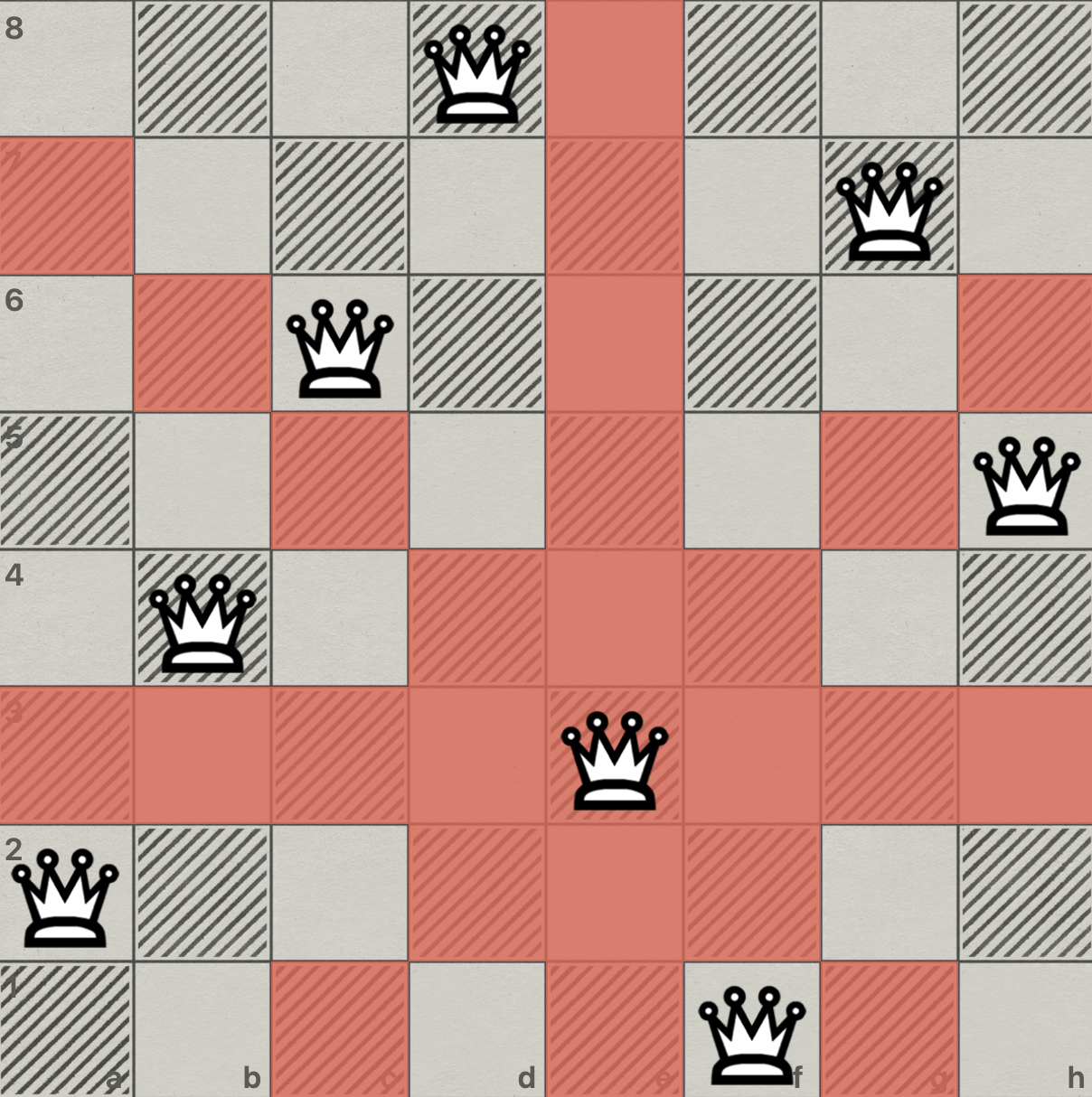
하지만 특정 유형의 SAT 문제에는 효율적인 해결 방법이 존재합니다. 대표적인 예시가 바로 n-queens 문제입니다. n-queens 문제는 n개의 체스 말을 서로 공격하지 않는 방식으로 배치하는 문제입니다. z3와 같은 SAT solver를 사용하면, n이 100일 때의 n-queens 문제를 놀랍게도 대략 10초 안에 해결할 수 있습니다.
SMT 구문(syntax) 및 도구
지금까지 우리는 SAT, 즉 주어진 명제 논리 공식이 참인 값을 가지는지 여부를 판단하는 문제에 대해 알아보았습니다. 그렇다면 SMT(Satisfiability Modulo Theories)는 무엇일까요? SMT는 SAT의 확장된 형태로, 추가된 여러 이론들을 기반으로 한 SAT 문제라고 할 수 있습니다. 특히 우리가 주목하는 부분은 실수와 정수에 대한 선형 부등식을 다루는 이론입니다.
이게 무슨 말일까요? SAT가 명제 논리 공식의 참 또는 거짓을 판단하는 문제라면, SMT는 단순히 명제 논리 공식에 국한되지 않고, 보다 넓은 범위의 논리적 체계와 그에 해당하는 공리 집합을 포괄합니다. 예를 들어, 명제 논리 공식 대신 부등식을 다룬다면, 해당 부등식을 만족하는 변수의 값, 즉 ‘만족 할당’을 찾는 문제도 SMT의 범위 안에 포함됩니다.
이처럼 SMT는 명제 논리 공식뿐만 아니라, 실수나 정수에 대한 선형 부등식과 같은 다양한 이론을 적용하여 그 만족 가능성을 탐구하는, SAT보다 더 넓은 범위의 문제를 포함합니다.
예시 01.
- 공식: $(2a > b + c) \land (2b > c + d) \land (2c > 3d) \land (3d > a + c)$
-
만족 가능 여부: SAT
- 만족 할당: {a = 30, b = 27, C = 32, d = 21}
SMT(Satisfiability Modulo Theories) 문제를 해결하는 데는 Z3, YICES, CVC4와 같은 여러 강력한 도구들이 있습니다. 이러한 도구들을 사용하여 SMT 문제를 해결하기 위해서는, 각 도구에서 요구하는 구문에 맞게 명세를 작성해야 합니다. 다양한 도구들이 있음에도 불구하고, 다행히 이들은 모두 SMT-LIB 표준 구문을 사용하며, 특히 버전 2의 구문을 사용합니다.
z3 -smt2 file
만약 사용하고자 하는 도구가 Z3이며, 실행 파일의 이름이 ‘file’이라면, 위와 같이 몇몇 옵션을 커맨드 라인 인터페이스에 파이핑하여 도구를 실행할 수 있습니다. 이제 파일 내의 문장을 어떻게 적어야하는지 살펴보겠습니다.
set-logic
set-options
처음에는 위의 두 명령어를 사용하여 사용할 로직이나 옵션을 설정할 수 있습니다. 그러나 대부분의 경우에는 이미 디폴트 값이 설정되어 있어 필요하지 않을 수 있습니다.
declare-const
declare-fun
이 두 명령어는 각각 변수와 함수를 선언하는 데 사용됩니다.
(assert ...)
이 명령어는 실제로 공식을 포함하는 부분입니다.
(check-sat)
이 명령어는 SAT 문제를 실제로 해결하는 과정을 실행합니다.
(get-model)
이 명령어는 SAT 문제가 만족할 때, 해당하는 할당을 보여줍니다.
(* 2 a) and (+ b c)
(> (* 2 a) (+ b c))
<, >, =, >=, <=, +, *, or, not과 같은 모든 연산자는 접두사(prefix) 표기법으로 작성되어야 합니다. +, and, or는 여러 개의 인자를 받을 수 있으므로 반드시 2개의 인자를 가질 필요는 없습니다. 그러나 주의할 점은 * 연산자는 반드시 2개의 인자를 가져야 하며, 그 중 하나는 숫자여야 합니다. 이는 * 연산자가 선형이 아닌 경우 도구가 제대로 인식하지 못하거나 올바르게 동작하지 않을 수 있기 때문입니다. 아래의 다양한 예시들을 통해 SMT 솔버 구문에 대해 자세하게 살펴보겠습니다.
예시 01.
-
공식: $(2a >b + c) \ \land (2b >c + d)\ \land (2c > 3d)\ \land (3d> a + c)$
-
코드
(declare-const a Int) (declare-const b Int) (declare-const c Int) (declare-const d Int) (assert (and(> (* 2 a) (+ b c)) (> (* 2 b) (+ c d)) (> (* 2 c) (* 3 d)) (> (* 3 d) (+ a c)) )) (check-sat) (get-model) -
결과
sat (model (define-fun b () Int 27) (define-fun a () Int 30) (define-fun c () Int 32) (define-fun d () Int 21) )
예시 02.
-
코드
(declare-fun (Int) Int) (assert (and (> (* 2 (f 1)) (+ (f 2) (f 3))) (> (* 2 (f 2)) (+ (f 3) (f 4))) (> (* 2 (f 3)) (* 3 (f 4))) (> (* 3 (f 4)) (+ (f 1) (f 3))) )) (check-sat) (get-model)예시 01.에서와 동일한 공식을 함수를 통해 표현한 예시입니다.
예시 03.
-
공식: $(A \leftrightarrow (D \land B)) \land (C \rightarrow B) \land \neg(A \lor B \lor \neg D) \land ((\neg A \land C)\lor D)$
-
코드
(declare-const A Bool) (declare-const B Bool) (declare-const C Bool) (declare-const D Bool) (assert (and (iff A (and D B)) (implies C B) (not (or A B (not D))) (or (and (not A) C) D) )) (check-sat) (get-model)위의 내용은 SMT 솔버에서 SAT 문제를 기술하는 방법에 대한 예시입니다. $\leftrightarrow$ (양방향 함의)와 $\rightarrow$ (단방향 함의)가 어떻게 표현되는지 주의 깊게 살펴보세요.
예시 04.
-
공식: $C = \dfrac{87 * 98798798987987987987987923423 + 98 * 763429999988888888887383489343}{2}$
-
코드
(declare-const A Int) (declare-const B Int) (declare-const C Int) (assert (and (= A 9879879898798798798798792342) (= B 763429999988888888887383489343))) (= (+ (* 87 A) (* 93 B) (+ C C) )) (check-sat) (get-model)이 코드는 정수형 상수 A, B, C를 선언한 후, A와 B에 매우 큰 값을 할당합니다. 그리고 이들 값에 대해 특정한 수식을 계산하도록
assert명령을 사용합니다. 여기서 중요한 점은, 마지막assert문에서 계산 결과가 참이 되도록 C의 값을 조정하는 것입니다. 이를 통해 SMT 솔버는 주어진 조건을 만족하는 C의 값을 찾아내며, 이 과정에서 복잡하고 큰 수에 대한 계산을 효율적으로 처리할 수 있음을 확인할 수 있습니다.
예시 05.
-
코드
(ite (< a b) 13 (* 3 a))ite는 if-then-else를 의미합니다. 이 코드는 파이썬이나 C와 같은 다른 프로그래밍 언어에서 볼 수 있는 삼항 연산자의 기능을 수행합니다. 주어진 조건이 참(true)일 경우 두 번째 항이 결과값으로 선택되고, 거짓(false)일 경우 세 번째 항이 결과값으로 선택됩니다. 여기서 중요한 점은, 조건문은 반드시 불리언(bool) 값으로 평가되어야 한다는 것입니다.
예시 06.
-
코드
(+ (ite p 1 0) (ite q 1 0) (ite r 1 0) )이 코드는 삼항 연산자를 활용한 또 다른 예시입니다. 여기서 각
ite구문은 조건p,q,r중 어떤 것이 참일 경우에 1을, 그렇지 않을 경우에는 0을 반환하도록 설정되어 있습니다. 이를 통해 여러 조건에 따른 결과값들의 합을 계산할 수 있습니다.
SMT Solver를 통한 8-Queens 문제 해결
8-queens 문제는 체스판 위에 8개의 퀸을 서로 공격할 수 없는 방식으로 배치하는 문제입니다. 이 문제에는 몇 가지 중요한 제약 조건이 있습니다. 첫 번째로, 같은 행이나 열, 대각선 위에 두 퀸이 위치할 수 없습니다. 이 문제를 해결하기 위해서는 이러한 제약 조건들을 만족하는 퀸의 위치를 찾아야 합니다.
우리의 목표는 이 문제를 직접 해결하는 것이 아니라, 문제의 조건을 정확하게 명세하여 Z3와 같은 SMT(Satisfiability Modulo Theories) 솔버에 입력하는 것입니다. SMT 솔버는 제공된 조건을 만족하는 해를 자동으로 찾아줍니다. 그렇다면 어떻게 8-queens 문제를 SMT 솔버가 이해할 수 있는 방식으로 명세할 수 있을까요?
변수 설정

8-queens 문제를 해결하기 위해, 체스 판의 각 칸에 대해 변수를 할당하고, 해당 칸에 퀸이 존재하는지 여부를 나타내는 방식으로 접근할 수 있습니다. 이러한 접근 방식에서, 각 변수는 불리언(Boolean) 값(True 또는 False)을 가지며, 퀸이 해당 칸에 존재하면 True, 존재하지 않으면 False로 설정됩니다.
행 제약조건 명세

8x8 체스판에서 8개의 퀸을 배치하는 문제는 각 열과 행에 퀸이 하나만 존재해야 하고, 대각선 방향으로도 퀸이 서로 공격할 수 없어야 합니다. 여기서는 동일한 행에 존재하는 변수들에 대해 설명하고 있습니다.
\[p_{i1},\ p_{i2},\ p_{i3},\ p_{i4},\ p_{i5},\ p_{i6},\ p_{i7},\ p_{i8}\]위의 변수들은 모두 i번째 행에 존재하는 변수들로, 여기서 i는 해당 행의 번호를 나타냅니다. 이 변수들은 해당 위치에 퀸이 존재하는지를 나타내는 불리언 변수입니다.
\[p_{i1}\lor p_{i2}\lor p_{i3}\lor p_{i4}\lor p_{i5}\lor p_{i6}\lor p_{i7}\lor p_{i8}\]한 행에 최소 한 개의 퀸이 존재해야 한다는 조건은 위와 같이 표현됩니다. 이 식은 i번째 행에 적어도 하나의 퀸이 존재함을 의미합니다.
\[\bigvee\limits_{\substack{j=1\\}}^8 p_{ij}\]동일한 식을 더 간결하게 표현하면 위와 같습니다.
\[\bigwedge\limits_{0 < j < k \leq8} (\neg p_{ij} \lor \neg p_{ik})\]한 행에 2개 이상의 퀸이 존재해서는 안 된다는 제약조건은 위와 같이 명세됩니다. 이는 i번째 행에 있는 모든 변수들에 대해, 두 변수의 조합이 모두 참이 되는 경우를 배제하는 것입니다. 즉, 한 행에는 오직 하나의 퀸만 배치될 수 있음을 나타냅니다. 이 조건은 중복되지 않는 모든 변수 쌍에 대해 “두 변수가 동시에 참이 될 수 없다”는 것을 명시함으로써, 한 행에 하나의 퀸만 존재할 수 있도록 합니다.
\[\bigwedge\limits_{i=1}^8\bigvee\limits_{\substack{j=1\\}}^8 p_{ij}\] \[\bigwedge\limits_{i=1}^8\bigwedge\limits_{0 < j < k \leq8} (\neg p_{ij} \lor \neg p_{ik})\]i번째 행에서 만족해야 하는 명세 표현을 확장하면, 위와 같이 모든 행에 대한 조건을 명확하게 표현할 수 있습니다.
열 제약조건 명세
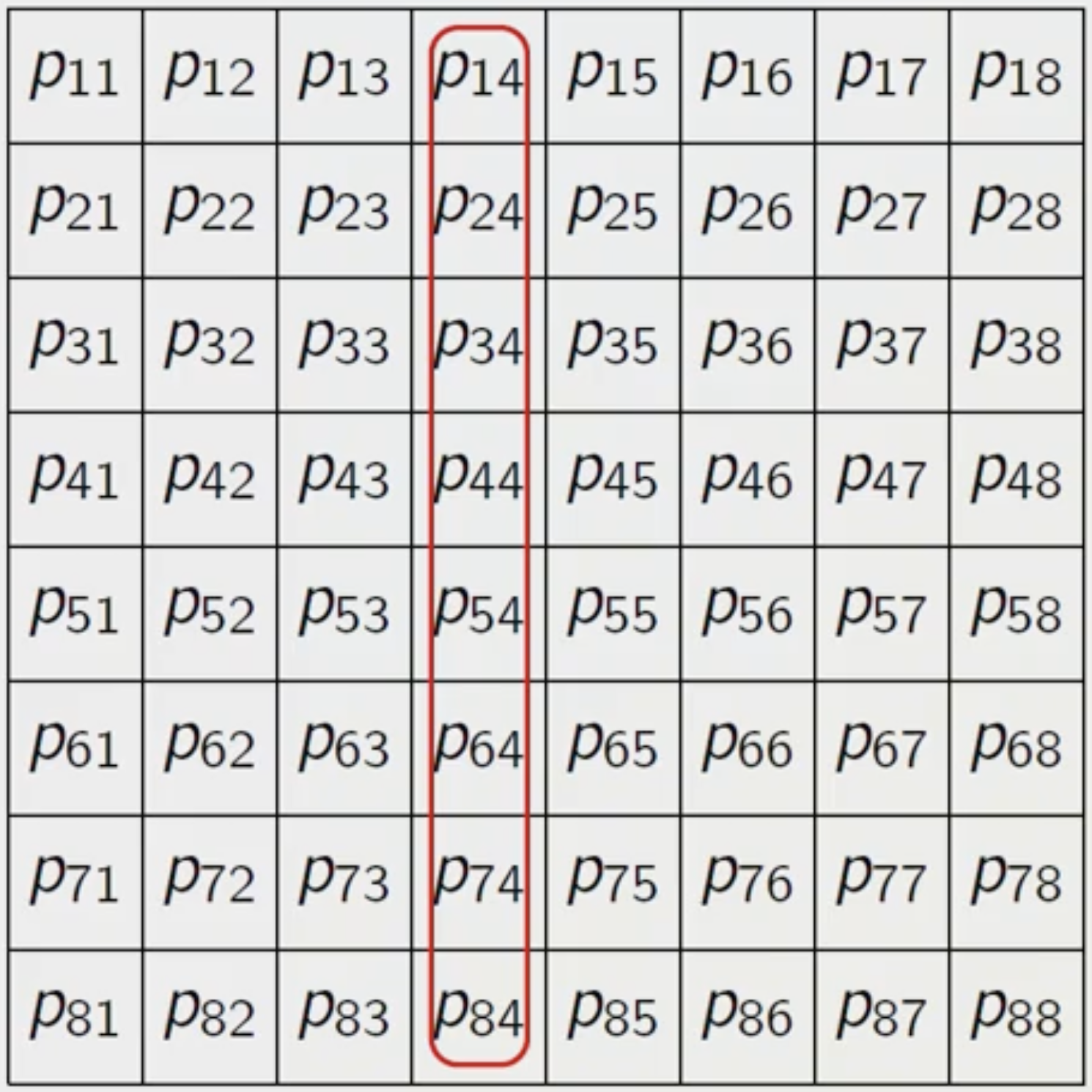
열 제약조건 역시 행 제약조건과 동일한 구조를 가집니다.
\[\bigwedge\limits_{j=1}^8\bigvee\limits_{i=1}^8 p_{ij}\] \[\bigwedge\limits_{j=1}^8\bigwedge\limits_{0 < i < k \leq8} (\neg p_{ij} \lor \neg p_{kj})\]위 두 식을 통해, 체스판에서 퀸들이 서로 공격할 수 없도록 열에 대한 제약조건을 명확하게 정의했습니다.
대각선 제약조건 명세
행과 열의 경우에는 아랫 첨자의 앞 수가 같거나 뒷 수가 같으면 동일한 행, 열이었는데, 동일한 대각선에 존재하는 변수들은 어떤 공통점이 존재할까요?

오른쪽 위를 향하는 대각선들에서는, 동일한 대각선 위의 변수들은 아랫 첨자의 앞 수와 뒷 수를 더한 값이 동일합니다.
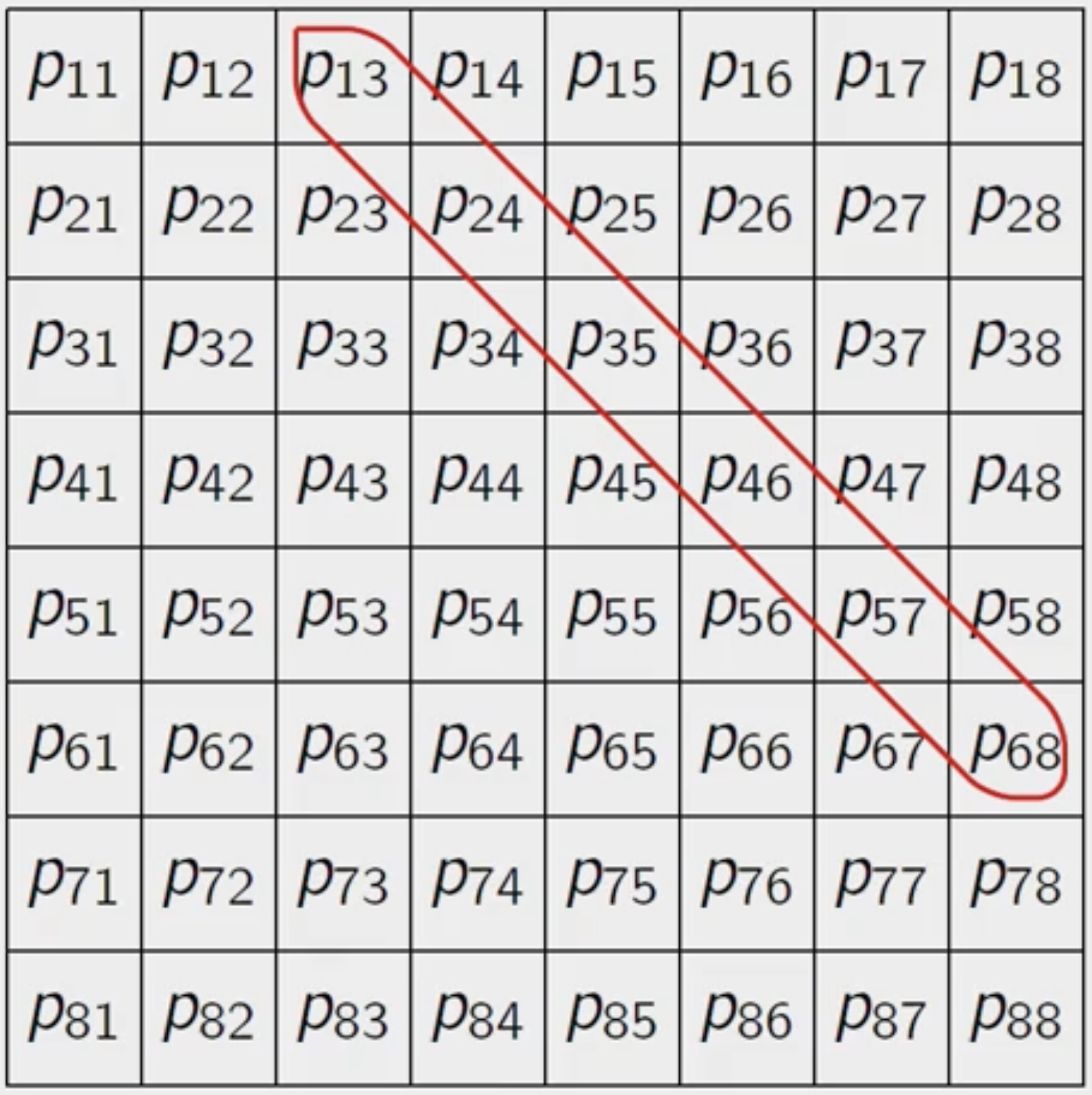
오른쪽 아래를 향하는 대각선들에서는, 동일한 대각선 위의 변수들은 아랫 첨자의 앞 수와 뒷 수의 차가 동일합니다.
전부 끝났습니다. 열, 행에서와 같이 각 대각선에 2개 이상의 퀸이 존재하면 안된다는 제약조건을 명세합니다. 퀸이 1개 이상 존재해야 한다는 제약조건은 필요하지 않습니다. 필요하지 않다기 보다도 사실 그런 제약조건은 8-queens 문제가 만족해야하는 조건에 해당되지 않습니다.
\[\bigwedge\limits_{0<i<i'\leq8}(\bigwedge\limits_{j, j': i+j=i'+j' \lor i-j=i'-j'} (\neg p_{ij} \lor \neg p_{i'j'}))\]축약되어 표현된 명세가 다소 복잡하지만, 대각선 제약조건이 정확하게 표현되어 있습니다.
명세를 축약된 표현으로 나타내 몇개 안돼 보이지만, 사실 8-queens 문제의 축약된 명세를 나열하면 요구사항의 개수가 740개나 됩니다. 이렇게 요구사항이 꽤 많은데도, SMT 솔버 도구를 사용해보면 해를 굉장히 빠른 시간 안에 찾아내는 것을 확인할 수 있습니다.
총 92개의 해가 존재하는데, SMT 솔버를 사용해서 해를 찾으면, 만족 할당을 한 개만 반환해줍니다. SMT 솔버가 발견한 만족 할당을 제약조건에 추가해서 그 해를 제외한 만족 할당만을 찾도록 하면 모든 해를 찾을 수 있습니다.
댓글남기기