로보틱스 06: 궤적 생성

---

이 포스팅은 ‘로보틱스‘에 대한 내용을 담고 있습니다.

자료 출처: 정슬, 로봇공학, 5판, 송재복, 로봇 팔의 설계 및 제어, F. C. Park and K. M. Lynch, Introduction to Robotics, John J. Craig, Introduction to Robotics (3rd Edition), https://www.youtube.com/watch?v=O1saBbqTx5Q&list=PLP4rlEcTzeFIvgNQD8M1T7_PzxO3JNK5Z&index=11

궤적 생성

로봇을 어떻게 움직이게 할 수 있는지를 살펴봤습니다. 시작 점과 끝 점이 있을 때 그 사이를 어떻게 이동할 지 결정하는 부분에 대해서 살펴봅니다.

머니퓰레이터를 이용해서 수행해야 하는 일은 초기 위치에서 마지막 위치로 옮기는 것인데요, 이 과정 사이를 어떻게 결정하는가에 따라 꽤나 다른 작동을 할 수 있습니다. 예를 들어, 우리가 팔을 옮길 때에도 초기 위치와 마지막 위치가 정해져 있을 때, 그 사이를 부드럽게 이동하는게 편하지, 휙휙 방향을 급격하게 전환시키면서 도달하는 것은 힘도 많이 들고 관절에도 무리를 주는 일입니다. 로봇도 동일합니다. 대부분의 경우에는 부드러운 경로를 따라 움직이는 것이 선호되고, 그렇게 했을 때 필요로 하는 에너지와 로봇 관절 부품들의 마모도가 낮아집니다. 때문에 보다 부드럽게 움직이게 하기 위해 단순히 마지막 형상만을 기술하는 것이 아니라 중간의 상세한 운동을 지정해주게 되는데요, 중간 지점에서 표시된 위치와 방위 지점을 경유점(Via Points)이라고 합니다. 당연하게도 부드러운 경로를 계획하는 방법은 수없이 많습니다. 그 중에 자주 사용되는 몇가지 방법들에 대해 살펴봅니다.

관절 공간의 경로 생성

가장 먼저 생각해볼 수 있는 것은, 관절 공간에서 경로를 생성하는 방법입니다. 우리가 시작하는 위치, 중간에 들르는 위치들, 그리고 마지막에 도달하는 위치에 가기 위한 관절의 각도는 역기구학을 통해 이미 구해진 상태입니다. 각 관절이 도달해야 하는 각도 포인트들이 구해진 상태에서, 그 사이를 어떻게 들를 것인지에 대해서 고민합니다. 이 방법은 계산이 쉽고, 기구의 특이성에 관련된 문제가 근본적으로 없다는 장점이 있습니다.

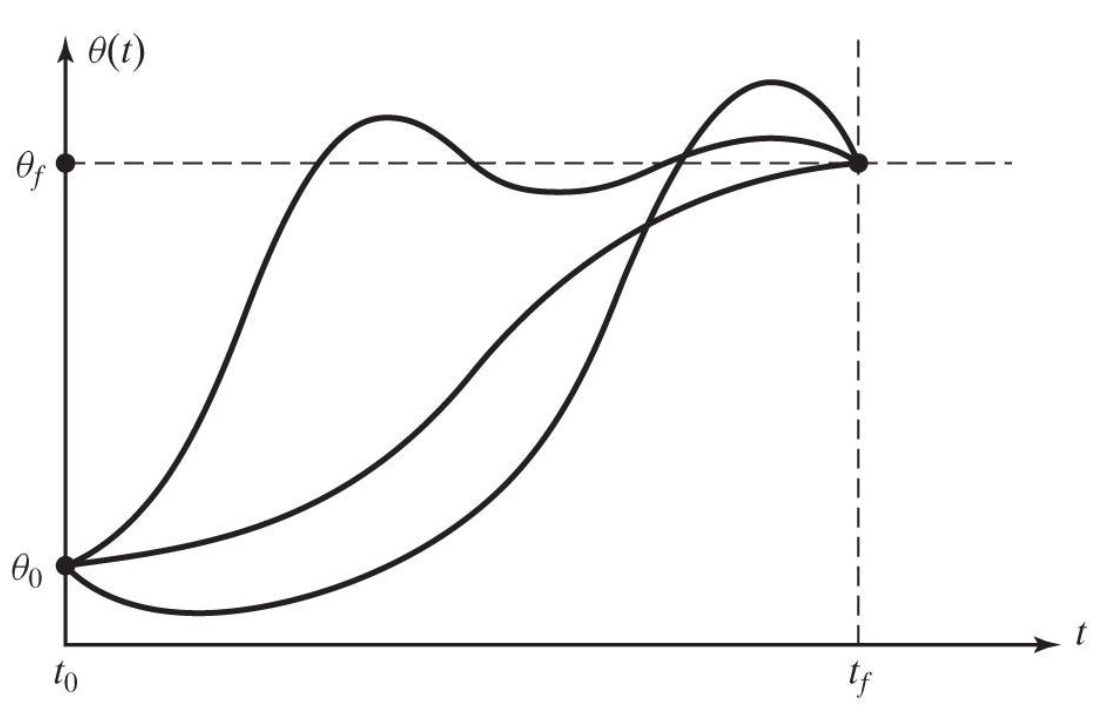
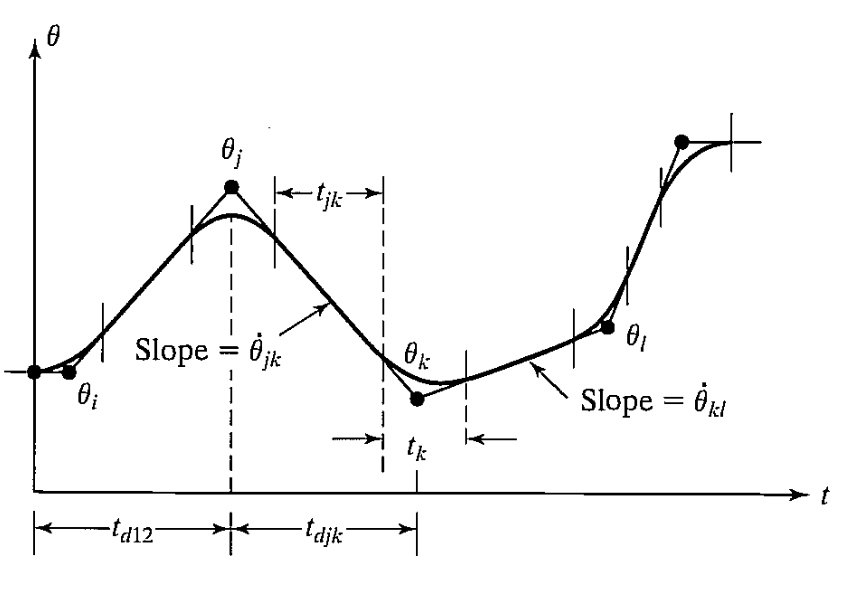
위의 그래프에서, 각도를 조정하는 경로로 총 3개로 제시합니다. 관절의 피로도를 생각할 때, 가운데의 단조 증가 함수의 경로로 관절을 제어하는게 괜찮아 보입니다. 관절이 움직임을 시작하는 속도가 0, 그리고 움직임을 끝마치는 속도도 0일 때, 그 사이를 부드럽게 이어주는 가장 간단한 형태는 3차 다항식입니다. 때문에 3차 다항식을 풀어 관절의 움직임을 결정하고, 이 방식을 3차 다항식 경로 생성법이라고 합니다.

\[\theta(t) = a_0 + a_0x + a_2t^2 + a_3t^3\] \[\theta(0) = \theta_0\] \[\theta(f) = \theta_f\] \[\dot\theta(0) = \dot\theta_0\] \[\dot\theta(f) = \dot\theta_f\]

관절이 시작하는 각의 위치와 끝나는 각의 위치, 그리고 시작하는 속도와 끝나는 속도를 0으로 설정하기 때문에 3차 다항식을 구할 수 있습니다.

\[a_0 = \theta_0\] \[a_1 = 0\] \[a_2 = \frac{3}{t^2_f}(\theta_f - \theta_0)\] \[a_3 = -\frac{3}{t^3_f}(\theta_f - \theta_0)\]

위의 식들을 사용해서 시작 지점의 각, 끝 지점의 각을 넣어 관절의 경로를 설정합니다. 그런데 생각을 해보면, 꼭 시작 지점의 속도가 0일 필요는 없어 보입니다. 예를 들어, 우리가 경유지점을 설정한다고 했을 때, 그 기점을 스치듯 움직이면서 지나치면 되는 일이지, 굳이 그 자리에서 서서히 멈췄다가 다시 서서히 출발할 필요는 없습니다. 때문에 시작 지점과 끝 지점의 속도를 0이 아닌 다른 숫자로 설정하는 경우를 생각해야되고, 그런 경우에 계수는 아래와 같이 결정됩니다.

\[a_0 = \theta_0\] \[a_1 = \dot\theta_0\] \[a_2 = \frac{3}{t^2_f}(\theta_f - \theta_0) - \frac{2}{t_f}\dot\theta_0 - \frac{1}{t_f}\dot\theta_f\] \[a_3 = -\frac{3}{t^3_f}(\theta_f - \theta_0) + \frac{1}{t^2_f}(\dot\theta_f + \dot\theta_0)\]

경유점에서 원하는 속도를 지정하는 방법

그렇다면 경유점에서 원하는 속도를 지정하는 방법에는 뭐가 있을까요? 단순하게는 우리가 경유점을 직교좌표계상의 말단부의 위치와 방위, 그리고 선속도와 각속도로 지정하는 방법이 있을 수 있습니다. 그런데 이 방법을 사용하게 되면, 그 지점에서의 역기구학 해를 구해야 될 텐데요, 역기구학을 푼다는 것은 굉장히 복잡한 일이기 때문에 잘 사용되는 방법은 아닙니다. 자주 사용되는 방법은 아래와 같습니다.

• 직교좌표 공간이나 관절 공간에서 휴리스틱(Heuristic)으로 시스템이 경유점들에서의 속도를 자동적으로 선택
• 경유점들에서의 가속도를 연속으로 하도록 시스템이 경유점들에서의 속도를 자동적으로 선택

휴리스틱을 통한 경유점의 속도 지정

휴리스틱이라는 말은 증명되지 않은, 그러니까 대충 해보니까 좋았던 방법들을 의미하는데요, 정말 생각보다 나쁘지 않은 방법입니다.

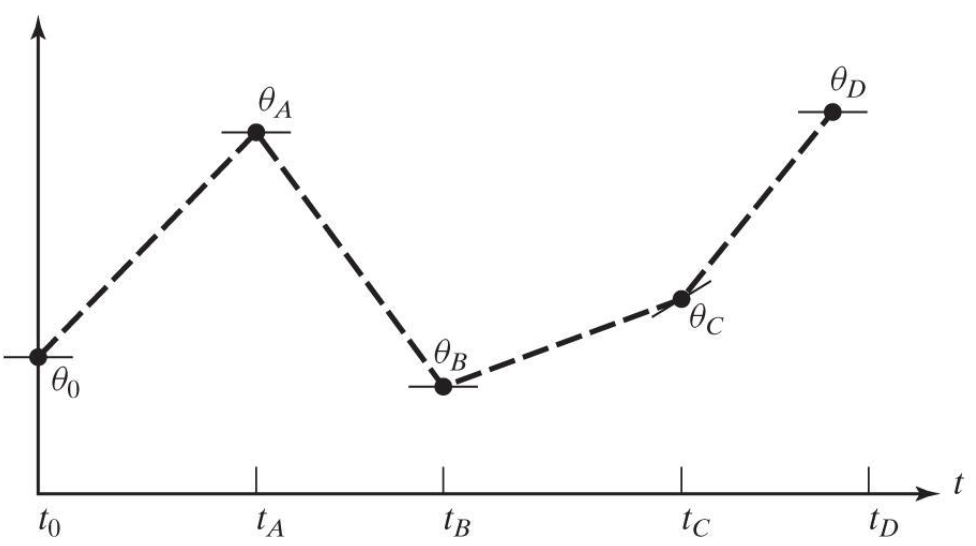
예를 들어 위와 같이 들러야 하는 지점이 총 5개가 주어졌을 때, 방향이 바뀌는 경우들($\theta_A$, $\theta_B$)에서는 속도를 0으로 설정하고, 방향이 바뀌지 않는 곳들($\theta_C$)에서는 속도를 앞, 뒤 직선들의 평균값으로 설정합니다.

가속도를 연속으로 하도록 경유점들의 속도 지점

여기에는 크게 두 가지 방법이 있습니다. 하나는 스플라인 해법을 통해 두개의 3차식을 연결하는 방법과 다른 하나는 아예 고차 다항식을 푸는 방법입니다.

스플라인 해법

\[\theta(t) = a_{10} + a_{11} + a_{12}t^2 + a_{13}t^3\] \[\theta(t) = a_{20} + a_{21} + a_{22}t^2 + a_{23}t^3\]

스플라인 해법에서는 위와 같이 총 2개의 3차식을 풀게 됩니다. 시작 속도와 종단 속도, 그리고 중간 지점에서의 위치와 속도, 가속도가 동일하다는 조건이 있기 때문에 두 3차식의 계수를 구할 수 있습니다.

\[a_{10} = \theta_0\] \[a_{11} = 0\] \[a_{12} = \frac{12\theta_v - 3\theta_g - 9\theta_0}{4t^2_f}\] \[a_{13} = \frac{-8\theta_v +3\theta_g +5\theta_0}{4t^3_f}\] \[\] \[a_{20} = \theta_v\] \[a_{21} = \frac{3\theta_g - 3\theta_0}{4t_f}\] \[a_{22} = \frac{-12\theta_v + 6\theta_g + 6\theta_0}{4t^2_f}\] \[a_{23} = \frac{8\theta_v -5\theta_g -3\theta_0}{4t^3_f}\]

고차 다항식

스플라인 해법이 아닌 고차 다항식을 사용할 수도 있데요, 이 경우 5차 다항식을 사용하게 되고, 시작 점과 끝 점의 가속도를 추가 제약으로 활용해 다항식의 계수를 얻을 수 있습니다.

\[a_0 = \theta_0\] \[a_1 = \dot\theta_0\] \[a_2 = \frac{\ddot\theta_0}{2}\] \[a_3 = \frac{20\theta_f - 20\theta_0 - (8\dot\theta_f + 12\dot\theta_0)t_f - (3\ddot\theta_0 - \ddot\theta_f)t^2_f}{2t^3_f}\] \[a_4 = \frac{30\theta_0 - 30\theta_f + (14\dot\theta_f + 16\dot\theta_0)t_f + (3\ddot\theta_0 - 2\ddot\theta_f)t^2_f}{2t^4_f}\] \[a_5 = \frac{12\theta_f - 12\theta_0 - (6\dot\theta_f + 6\dot\theta_0)t_f - (\ddot\theta_0 - \ddot\theta_f)t^2_f}{2t^5_f}\]

포물선과 혼합된 직선

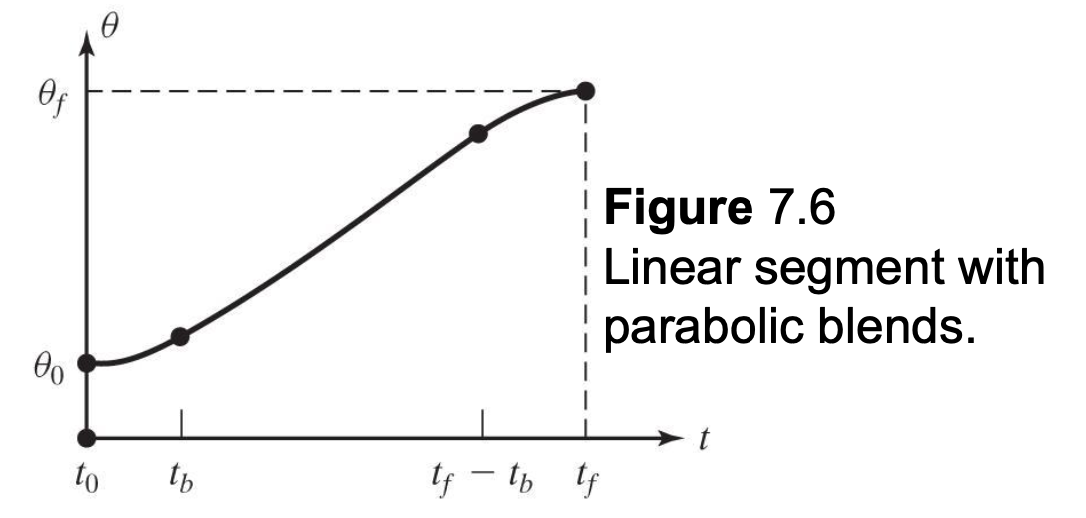
3차 다항식, 그리고 5차 다항식으로 경로를 계획하는 방법들에 대해서 살펴보았는데, 부드러워서 좋기는 한데 생각보다 조금 비효율적으로 움직이는 측면이 없지 않습니다. 사실 모든 구간에서 가속도 운동을 할 필요는 없습니다. 대신에 처음에 가속을 조금 더 빠르게 하고 등속도 운동을 한 다음 다시 속도를 내리는 방법을 생각해볼 수 있는데요, 이 방식을 LSPB(Linear Segment with Parabolic Blends) 알고리즘이라고 부릅니다.

시작과 끝 지점은 점대칭이기 때문에, 처음에 가속하는 부분만 구하면 끝 부분의 계획은 자동으로 결정됩니다. 중간 지점의 시간을 $t_h$, 그리고 그 지점에서의 각도를 $\theta_h$라고 하겠습니다. 또, 직선이 시작되는 지점의 각도를 $\theta_b$라고 부르겠습니다.

\[\ddot\theta t_b = \frac{\dot\theta_h - \dot\theta_b}{t_h - t_b}\]

가속도를 시간에 대해서 한 번 적분하면 속도, 직선의 기울기와 동일합니다.

\[\theta_b = \theta_0 + \frac{1}{2}\ddot\theta t^2_b\]

그리고 가속도를 시간에 대해 2번 적분하고 초기값을 더하면 직선의 시작 위치와 동일합니다. 위 두 식을 이용해 포물선의 식을 결정할 수 있는데요, 모든 경우에 해가 존재하는 것은 아닙니다. 당연히 그럴 수밖에 없는 이유는 처음 속도와 마지막 속도, 그리고 시간이 정해져 있기 때문에, 불가능한 경우가 반드시 존재합니다. 이는 아래의 판별식을 통해 확인할 수 있습니다.

\[\ddot\theta \geq \frac{4(\theta_f - \theta_0)}{t^2}\]

아래는 LSPB를 경유점들에 적용해 얻은 경로인데요, 아래 그래프에는 치명적인 문제점이 있습니다. 바로 우리가 지정한 각도에 도달하기 전에 방향을 틀어버린다는 점입니다.

위의 문제점을 해결하기 위해 가상 경유점(Pseudo Via Points)를 지정할 수 있습니다. 유사 경유점은 경유점을 대칭으로 하는 점으로 적당히 결정됩니다(다항식을 쓰든, LSPB를 쓰든, 두 점의 가운데 지점은 무조건 지나기 때문).

직교좌표 공간법

위의 관절 공간에서 경로를 계획하면 말단부는 관절의 움직임에 맞춰 움직이게 됩니다. 혼동하지 않아야 하는 점은, 관절 공간에서 직선 운동을 했다고 해서 말단부가 직교좌표 공간상에서 직선운동을 하는 것은 절대 아니라는 사실입니다. 예를 들어, 글씨를 쓰는 작업이나 용접 작업 같은 일에서는 관절부의 경로가 아닌, 말단부의 경로를 정확하게 지정해야 합니다.

\[{^S\chi_A} = \begin{bmatrix} {^SP_{A\space Origin}} \\ {^SK_A} \end{bmatrix}\]

우리가 원하는 직교좌표상의 말단부의 위치와 자세를 포함하는 행렬을 위와 같이 표기합니다. 이 때, 말단부의 자세는 각-축 표현으로 합니다. 모든 경로점이 이렇게 표시되면, 경로점에서 경로점으로의 운동을 스플라인 함수로 나타낼 수 있습니다.

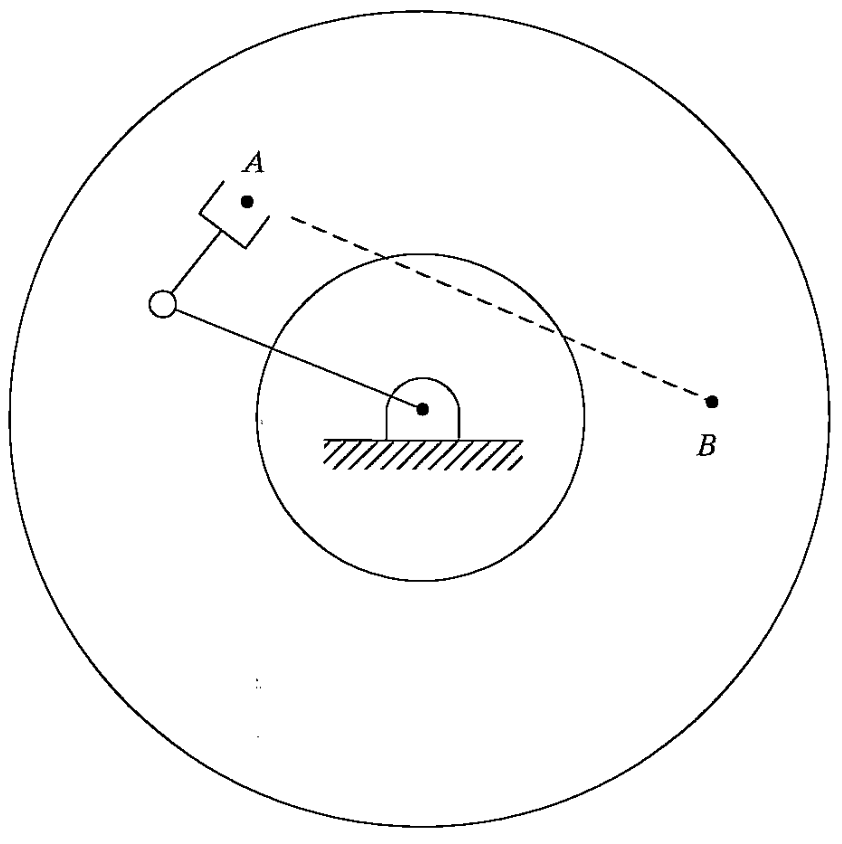
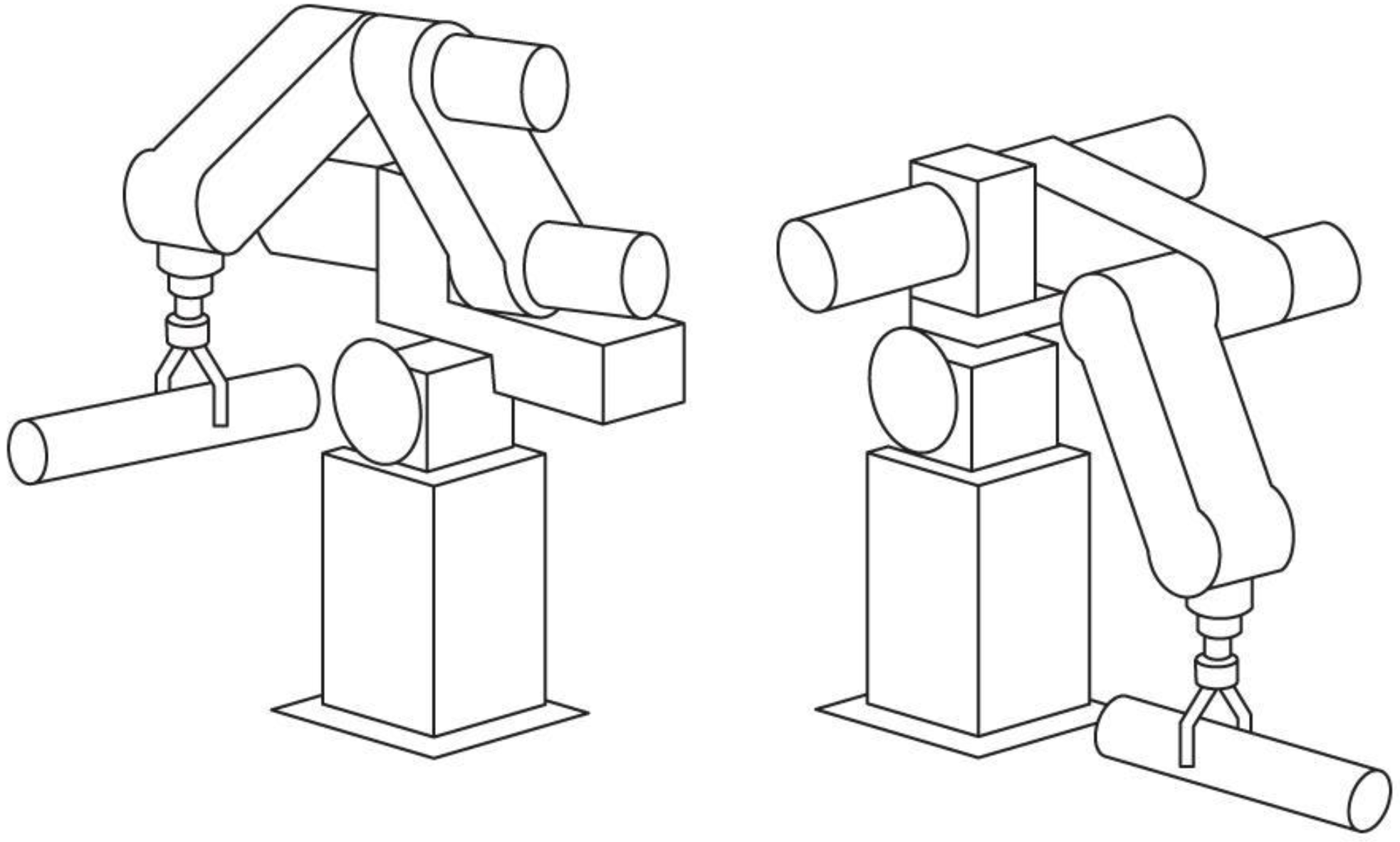
직교좌표 경로 계획에서는 관절 공간 경로 계획에서와 달리 여러 기하학적인 문제들이 발생합니다. 그 대표적인 사례가 위의 그림에서 나타납니다. 예를 들어, 우리는 손을 배 앞에 위치시킬 수 있고, 등 뒤에 위치시킬 수 있습니다. 그렇다고 몸을 뚫고 손을 직선운동할 수 있는 것은 아닙니다. 로봇도 마찬가지 입니다. 단순히 직선운동을 계획하면 도달할 수 없는 중간점들이 발생할 수 있습니다.

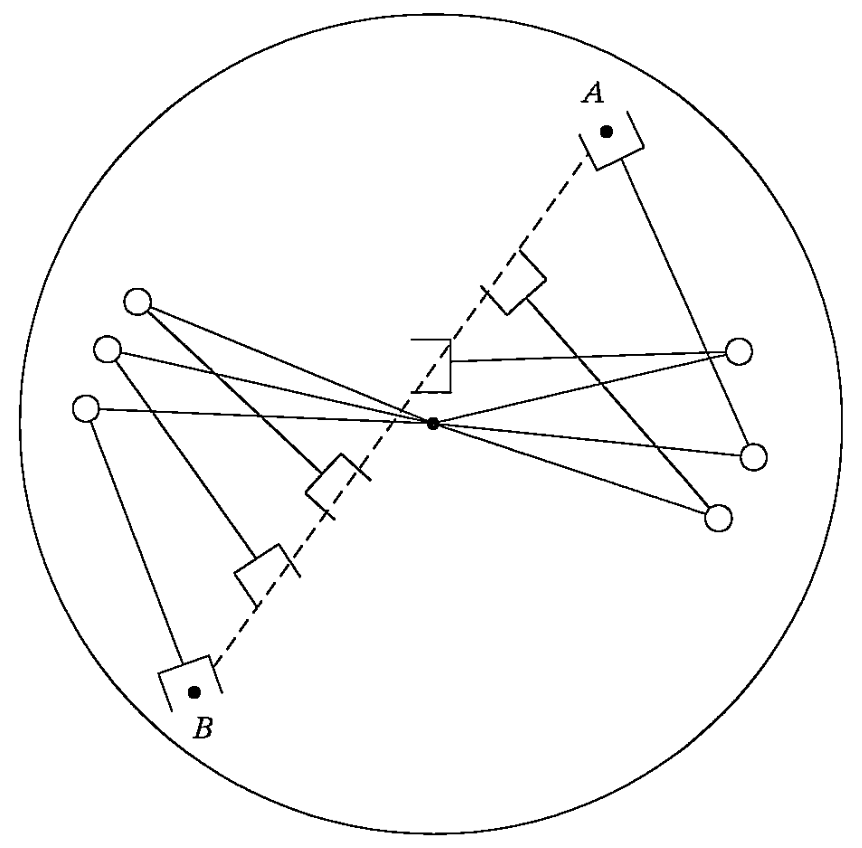
발생할 수 있는 또 다른 문제점은, 특이점 근처에서 지나치게 높은 가속도가 필요될 수 있다는 점입니다. 위 그림의 로봇은 두 링크의 길이가 같기 때문에 원 내부의 모든 공간을 지나칠 수 있는데요, 로봇이 기저 좌표의 원점 근처를 통과하는 순간 1번 관절의 위치가 반대 방향으로 이동해야 합니다. 이 때 굉장히 큰 토크를 필요로 하게 되는데, 이 경우 로봇이 수행할 수 없거나 로봇 관절의 손상을 야기할 수 있습니다.