로보틱스 05: 동역학
이 포스팅은 ‘로보틱스‘에 대한 내용을 담고 있습니다.
자료 출처: 정슬, 로봇공학, 5판, 송재복, 로봇 팔의 설계 및 제어, F. C. Park and K. M. Lynch, Introduction to Robotics, John J. Craig, Introduction to Robotics (3rd Edition), https://www.youtube.com/watch?v=O1saBbqTx5Q&list=PLP4rlEcTzeFIvgNQD8M1T7_PzxO3JNK5Z&index=11
동역학
이전 포스팅에서는 각 관절과 말단부의 속도 관계와 정지한 상태에서의 정적 힘의 관계에 대해서 다뤘습니다. 그런데 우리가 로봇팔을 사용하는 상황을 생각해보면, 이것만으로 충분하지 않습니다. 예를 들어서 자동차를 조립하는 로봇은 철판을 들고 조립 위치까지 움직여야 합니다. 이 과정에서 로봇은 움직이는 과정중에 지속적으로 힘이 필요합니다. 다시 말해, 정적 힘이 아닌 동적 힘을 계산할 수 있어야 로봇 팔의 가속과 힘을 결정할 수 있습니다. 이 포스팅에서는 로봇 팔을 움직이는 과정 중의 힘인 동적 힘, 동역학에 대해서 다룹니다.
동역학이란 무엇인가
동역학 역시 기구학과 마찬가지로 관절과 말단부의 관계에 대한 것입니다. 구체적으로 동역학에서의 관심 대상은 궤도점(말단)의 위치, 속도, 그리고 가속도($\Theta$, $\dot\Theta$, $\ddot\Theta$)와 관절 토크 벡터($\tau$)의 관계입니다. 반대로 관절 토크 벡터를 이렇게 설정했을 때, 궤도점은 어떻게 운동하는가 역시 동역학에서 다루는 문제입니다.
강체의 가속
힘은 가속과 동일한 개념이기 때문에 강체의 가속에 대해서 먼저 규정하겠습니다.
\[{^B\dot V_Q} = \frac{d}{dt}{^BV_Q}=\lim_{\Delta t \rightarrow 0}\frac{ {^BV_Q} (t+\Delta t) - {^BV_Q}(t)}{\Delta t}\] \[{^B\dot \Omega_Q} = \frac{d}{dt}{^B\Omega_Q}=\lim_{\Delta t \rightarrow 0}\frac{ {^B\Omega_Q}(t+\Delta t) - {^B\Omega_Q}(t)}{\Delta t}\] \[\dot v_A = {^U \dot V_{A \space Origin}}\] \[\dot \omega_A = {^U \dot \Omega_{A \space Origin}}\]속도와 각속도 벡터는 알고자 하는 점의 위치와 각을 시간에 대해 미분해 얻을 수 있었습니다. 가속도와 각가속도는 속도와 각속도를 시간에 대해 한 번 더 미분하여 얻을 수 있습니다. 속도와 각속도에서 우주 좌표계(${U}$)에 대한 속도와 각속도를 그리스 소문자로 표기했었는데요, 가속도와 각가속도에서 똑같은 관례를 따릅니다.
선가속도
먼저, 속도에 대한 식을 유도하는 중간에 만났던 식에서부터 살펴보겠습니다.
\[{^AV_Q} = {^A_BR{^BV_Q}}+{^A\Omega_B}\times {^A_BR{^BQ}}\]위 식은 속도를 유도할 때 구했던 마지막 식이 아닌데요, 계${A}$ 상에서의 계${B}$의 속도가 포함되어있지 않습니다. 속도에서와 마찬가지로 유도의 가장 마지막에 별도로 추가합니다. 계${A}$ 상에서의 계${B}$의 속도는 ${A}$관절에 의해서 발생하게 되는데, 이는 다른 속도들과 독립적이기 때문에 나중에 추가해도 결과에 차이가 발생하지 않습니다. 아무튼 위 식을 한 번 미분해보겠습니다.
\[\frac{d}{dt}{^AV_Q} = \frac{d}{dt}({^A_BR{^BV_Q}})+\frac{d}{dt}({^A\Omega_B}\times {^A_BR{^BQ}})\]우항의 첫 번째 항은 그대로 두고, 두 번째 항을 곱미분의 형태로 풀면 아래와 같습니다.
\[\frac{d}{dt}{^AV_Q} = \frac{d}{dt}({^A_BR{^BV_Q}})+[{^A\dot\Omega_B}\times {^A_BR{^BQ}} + {^A\Omega_B}\times \frac{d}{dt}({^A_BR{^BQ}})]\]이 식을 정리하고, 계${A}$ 상에서의 계${B}$의 가속도 별도로 추가하면 아래와 같습니다.
\[{^A\dot V_Q} = {^A\dot V_{B \space Origin}} + {^A_BR{^B\dot V_Q}} + 2{^A\Omega_B} \times {^A_BR{^BV_Q}} + {^A\dot\Omega_B} \times {^A_BR{^BQ}} + {^A\Omega_B} \times ({^A\Omega_B} \times {^A_BR{^BQ}})\]식이 꽤나 복잡한데요, 회전 관절일 경우의 링크의 선가속도는 회전의 방식과 거리가 고정되는 몇 가지 요소 덕분에 보다 간단하게 나타납니다.
\[{^A\dot V_Q} = {^A\dot V_{B \space Origin}} + {^A\Omega_B} \times({^A\Omega_B} \times {^A_BR{^BQ}}) + {^A\dot\Omega_B} \times {^A_BR{^BQ}}\]각가속도
각가속도는 선가속도에 비해 훨씬 더 간단합니다. 이전에 각속도에 대해 따로 일반적인 식의 형태를 다룬 적은 없는데요, 두 계 사이의 각속도의 관계는 아래와 같습니다.
\[{^A\Omega_C} = {^A\Omega_B} + {^A\Omega_C}\]너무 당연하게 받아들여지는 식입니다. 회전행렬을 사용해 좀 더 구조를 드러내 보겠습니다.
\[{^A\Omega_C} = {^A\Omega_B} + {^A_BR}{^B\Omega_C}\]이제 시간에 대한 미분을 통해 각가속도를 구하면 아래와 같습니다.
\[{^A\dot\Omega_C} = {^A\dot\Omega_B} + {^A_BR}{^B\dot\Omega_C} + {^A\Omega_B} \times {^A_BR}{^B\Omega_C}\]질량 분포
각가속도를 유도하는 식을 구해내긴 했는데, 중요한 사실을 하나 다루지 않았습니다. 그건 바로 토크와 각가속도의 관계입니다. 직선 운동을 하는 물체의 가속도와 힘의 관계는 $F=ma$라는 식으로 굉장히 익숙한데요, 사실 회전 운동의 경우도 용어와 기호가 다를 뿐 식의 구조는 동일합니다.
\[\tau = I\alpha\] \[F = ma\]위 식에서 $\tau$는 토크, $I$는 관성 모먼트(Moment of Inertia), 그리고 $\alpha$는 각가속도를 의미합니다. 회전하는 물체의 각가속도와 토크 사이의 관계는 물체의 전체 질량으로 설명되지 않습니다. 그리고 동일한 물체라고 할지라도 어떤 방향으로 돌리느냐에 따라 들어가는 토크의 힘은 달라집니다. 물체 내부의 질량 분포에 따라 결정되는 $I$라는 관성 모먼트를 도입해 물체의 회전 움직임을 거시적으로 설명합니다. 그리고 물체의 회전 방향에 따라 달라지는 관성 모먼트를 설명하기 위해, 축 방향에 따른 관성 모먼트를 텐서를 사용해 모두 설명하는데, 이를 관성 텐서라고 부릅니다.
\[{^AI} = \begin{bmatrix} I_{XX} & -I_{XY} & -I_{XZ} \\ -I_{XY} & I_{YY} & -I_{YZ} \\ -I_{XZ} & -I_{YZ} & I_{ZZ} \\ \end{bmatrix}\] \[I_{XX} = \int\int\int_V(y^2 + z^2)\rho \space dv\] \[I_{XY} = \int\int\int_V(xy)\rho \space dv\]$\int\int\int_V$은 모든 축방향에 대해 적분을 수행한다는 의미입니다. 따라서 $Volume$의 앞 철자인 $V$를 적분 기호의 밑첨자에 표기합니다. $\rho$는 밀도를 의미합니다. 즉, $I_{XX}$는 $x$축 방향의 거리의 제곱($=y^2 + z^2$)과 밀도를 곱해서 적분한 값입니다. $I_{XX}$를 관성 질량 모먼트라고 하고, $I_{XY}$와 같이 다른 축방향에 대한 관성 모먼트를 관성의 질량적이라고 부릅니다. 관성 질량 모먼트와 달리 관성의 질량적은 직관적으로 잘 받아들여지는 컨셉은 아닌데요, 보다 자세한 설명은 아래의 유튜브 영상에서 확인할 수 있습니다.
식에서 알 수 있듯, $XYZ$좌표계의 설정에 따라 관성 텐서 값을 달라집니다. 같은 물체를 다르게 회전시킬 때마다 이 값들을 전부 다시 계산하는 것은 꽤나 번거로운 일입니다. 다행히 이전에 구했던 관성 텐서와 평행하는 다른 축의 관성 텐서는 평행축 정리(Parallel-Axis Theorem)를 통해 보다 쉽게 구할 수 있습니다.
\[{^AI} = {^CI} + m[P^T_cP_cI_3 - P_cP^T]\]- 위 식에서 ${^CI}$는 Center of Mass를 지나치는 직선을 축으로 하는 좌표계에서 구한 관성텐서이고, $I_3$은 Identity Matrix 입니다.
뉴턴, 오일러의 방정식
뉴턴, 오일러 방정식에서는 링크의 질량 중심의 위치와 관성 텐서를 사용해 토크를 계산합니다.
힘이 링크의 질량 중심에 가해진다면, 힘이 가해진 방향으로 링크는 선가속을 받습니다.
우리가 야구공을 던지면 단순히 앞으로 선가속을 받을 뿐 아니라 공 자체가 각가속을 받는데요, 링크에서도 마찬가지로 선가속 뿐만 아니라 각가속이 존재하고, 위 식은 토크와 각가속 사이의 관계를 설명합니다.
반복 뉴턴-오일러의 동역학 공식
토크를 구하는 방식도 이전에 위치, 속도를 구했던 방식과 마찬가지로 이전 링크와 다음 링크 사이의 관계식을 차례차례 구하게 됩니다. 다만, 조금 더 복잡한 점이 있는데요, 동역학을 구할 때에는 기저에서 말단까지 전파를 한 다음, 다시 기저까지 되돌아오는 작업을 끝마쳐야 비로소 필요한 토크가 구해집니다.
- 외향 반복: 링크 1에서 링크 $n$까지 속도와 각가속도를 계산
- 내향 반복: 링크 $n$에서 링크 1까지 힘과 토크를 계산
외향 반복
각가속도
\[{^{i+1}\omega_{i+1}} = {^{i+1}_iR^i}\omega_i + \dot{\theta}_{i+1}{^{i+1}\hat{Z}_{i+1}}\]이전에 유도했던 각속도 공식인데요, 미분을 하면 아래와 같습니다.
\[{^{i+1}\dot\omega_{i+1}} = {^{i+1}_iR^i}\dot\omega_i + {^{i+1}_iR^i}\omega_i \times \dot{\theta}_{i+1}{^{i+1}\hat{Z}_{i+1}} + \ddot{\theta}_{i+1}{^{i+1}\hat{Z}_{i+1}}\]식을 보면 굉장히 많은 입력 변수를 필요로하는 것을 확인할 수 있는데요, 관절의 위치, 속도, 각속도($\Theta$, $\dot\Theta$, $\ddot\Theta$)는 우리가 조인트를 동작할 때 직접 결정하는 값입니다. 그렇기 때문에 사실상 이전 관절의 회전 속도와 회전 가속도만을 알면, 다음 관절의 회전 가속도를 구할 수 있습니다.
\[{^{i+1}\omega_{i+1}} = {^{i+1}_iR^i}\omega_i\]프리즘 관절의 경우, 회전과 관련된 변수가 미분을 하면 전부 날라가기 때문에 미분 결과가 좀 더 간단하게 나옵니다.
선가속도
\[{^{i+1}v_{i+1}} = {^{i+1}_iR}({^iv_i} + {^iw_i} \times {^{i}P_{i+1}})\]위 식도 마찬가지로 이전에 유도했던 선속도 공식인데요, 미분을 하면 아래와 같습니다.
\[{^{i+1}\dot v_{i+1}} = {^{i+1}_iR}[{^i\omega_i} \times {^iP_{i+1}} + {^i\omega_i} \times ({^iw_i} \times {^{i}P_{i+1}}) + {^i\dot v_i}]\] \[{^{i+1}\dot v_{i+1}} = {^{i+1}_iR}({^i\dot\omega_i} \times {^iP_{i+1}} + {^i\omega_i} \times ({^iw_i} \times {^{i}P_{i+1}}) + {^i\dot v_i}) + 2{^{i+1}\omega_{i+1}} \times \dot{d}_{i+1} {^{i+1}\hat Z_{i+1}} + \ddot d_{i+1}{^{i+1}\hat Z_{i+1}}\]내향 반복
\[F_i = m\dot v_{C_i}\] \[N_i = {^{C_i}I}\dot{\omega_i} +\omega_i \times {^{C_i}I}\omega_i\]위 식들은 이전에 힘과 토크를 설명한 식에 인덱스만 붙인 것입니다. 그리고 아래의 정의를 추가하겠습니다.
- $f_i$: 링크 $i-1$에 의해 링크 $i$에 가해지는 힘
- $n_i$: 링크 $i-1$에 의해 링크 $i$에 가해지는 토크
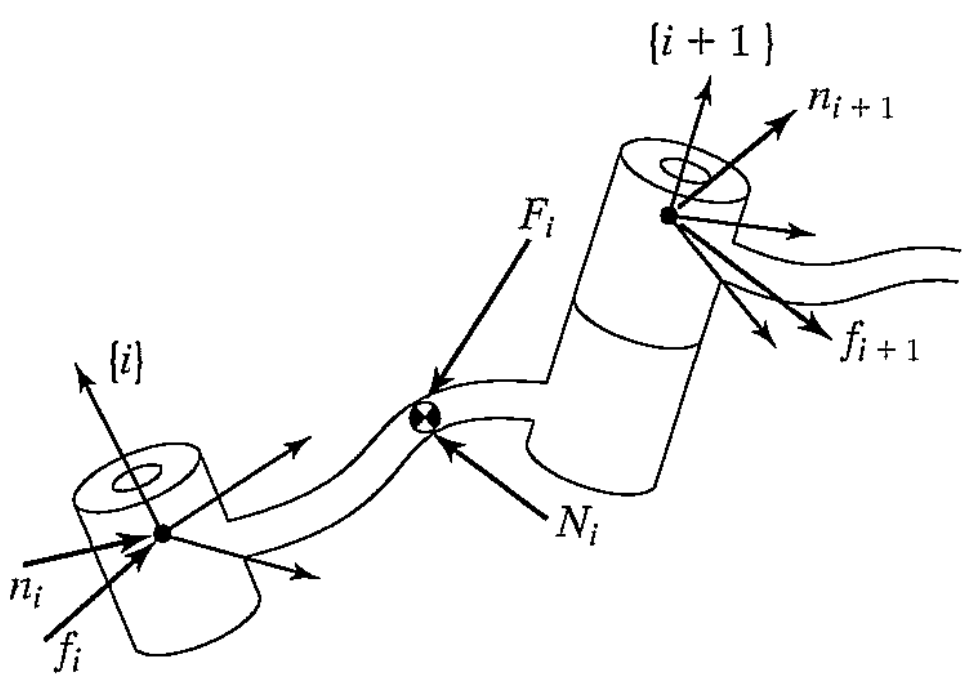
링크는 고정된 상태에서 힘의 평형관계를 유지합니다. 따라서 아래의 식을 얻게됩니다.
\[{^iF_i} = {^if_i} - {^i_{i+1}R^{i+1}}f_{i+1}\]토크도 비슷한 방식으로 정리하면 아래의 식을 얻을 수 있습니다.
\[{^iN_i} = {^in_i} - {^i_{i+1}R^{i+1}}n_{i+1} - {^iP_{C_i}} \times {^iF_i} - {^iP_{i+1}} \times {^i_{i+1}R}{^{i+1}f_{i+1}}\]마지막으로 식을 정리해 아래의 동역학 공식으로 표현됩니다.
\[{^if_i} = {^i_{i+1}R^{i+1}}f_{i+1} + {^iF_i}\] \[{^in_i} = {^iN_i} + {^i_{i+1}R^{i+1}}n_{i+1} + {^iP_{C_i}} \times {^iF_i} + {^iP_{i+1}} \times {^i_{i+1}R}{^{i+1}f_{i+1}}\]토크 힘을 구했으면, 관절이 조정할 수 있는 $Z$축의 토크 요소만을 따로 빼냅니다.
\[\tau_i = {^in_i^T}{^i\hat Z_i}(회전)\] \[\tau_i = {^if_i^T}{^i\hat Z_i}(프리즘)\]
순서를 살펴보면, 처음 관절의 힘과 토크를 알기 위해서는 속도와 가속도를 순전파를 한 뒤, 다시 토크와 힘을 역전파를 수행해 얻을 수 있습니다. 이러한 순서로 반복, 계산하는 알고리즘을 반복형 뉴턴-오일러 동역할 알고리즘이라고 부릅니다. 이 알고리즘을 사용하면 중력의 효과를 ${^0\dot v_0}$을 $G$로 설정함으로써 매우 간단하게 포함할 수 있습니다.
폐형식의 동역학 방정식
반복형 뉴턴-오일러 동역학 알고리즘을 통해 각 관절에서 필요한 토크값을 알아낼 수 있었는데요, 예를 들어 2-링크 평면 머니퓰레이터의 동역학 해석 결과만을 정리하면 아래와 같습니다.
\[\tau_1 = m_2l^2_2(\ddot\theta_1 + \ddot\theta_2) + m_2l_1l_2c_2(2\ddot\theta_1 + \ddot\theta_2) + (m_1 + m_2)l^2_1\ddot\theta_1 - m_2l_1l_2s_2\dot\theta^2_2 - 2m_2l_1l_2s_2\dot\theta_1\dot\theta_2 + m_2l_2gc_{12} + (m_1 + m_2)l_1gc_1\] \[\tau_2 = m_2l_1l_2s_2\ddot\theta_1 + m_2l_1l_2s_2\dot\theta^2_1 + m_2l_2gc_{12} + m_2l^2_2(\ddot\theta_1 + \ddot\theta_2)\]위 식을 ($\tau = M(\Theta)\ddot\Theta + V(\Theta,\dot\Theta) + G(\Theta)$)의 보다 간단한 형태로 정리하겠습니다.
\[M(\Theta) = \begin{bmatrix} l^2_2m_2 + 2l_1l_2m_2c_2 + l^2_1(m_1 + m_2) & l^2_2m_2 + l_1l_2m_2c_2 \\ l^2_2m_2 + l_1l_2m_2c_2 & l^2_2m_2 \end{bmatrix}\] \[V(\Theta, \dot\Theta) = \begin{bmatrix} -m_2l_1l_2s_2\dot\theta^2_2 -2m_2l_1l_2s_2\dot\theta_1\dot\theta_2 \\ m_2l_1l_2s_2\dot\theta^2_1 \end{bmatrix}\] \[G(\Theta) = \begin{bmatrix} m_2l_2gc_{12} + (m_1 + m_2)l_1gc_1 \\ m_2l_2gc_{12} \end{bmatrix}\]위의 식에서 $M(\Theta)$은 질량 행렬, $V(\Theta, \dot\Theta)$는 원심력과 코리올리 힘, 그리고 $G(\Theta)$는 중력항을 의미합니다. 이렇게 정리한 식을 형태 공간 방정식(State Space Equation)이라고 합니다. $V(\Theta, \dot\Theta)$은 원심력과 코리올리 힘이 포함된 벡터인데요, 코리올리($B$)와 원심력($C$)을 각각 분리해 식으로 표현할 수도 있습니다.
\[\tau = M(\Theta)\ddot\Theta + B(\Theta)[\dot\Theta \dot\Theta] + C(\Theta)[\dot\Theta^2] + G(\Theta)\] \[[\dot\Theta \dot\Theta] = \begin{bmatrix} \dot\theta_1\dot\theta_2 & \dot\theta_1\dot\theta_3 & ... & \dot\theta_{n-1}\dot\theta_n \end{bmatrix}\] \[[\dot\Theta^2] = \begin{bmatrix}\dot\theta^2_1 & \dot\theta^2_2 &...& \dot\theta^2_n\end{bmatrix}^T\]위와 같이 정리하고 나면, 토크가 오직 각도를 받는 함수값에 의해 결정됨을 알 수 있습니다. 이렇게 정리한 방정식을 자세 공간 방정식(Configuration Space Equation)이라고 조금 다르게 부릅니다.
동역학의 라그랑주 공식
여기까지 다룬 내용은 위치와 속도, 그리고 가속도를 통해 관절의 토크 값을 알아내는 방법이었습니다. 그런데 동역학을 해석하는 방법은 굉장히 다양한데요, 그 중 하나는 바로 역학적 에너지로 물체의 토크를 계산하는 방법입니다.
\[u_i = -m_i{^0g^T}{^0P_{C_i}} + u_{ref_i}\] \[u = \sum^n_{i=1}u_i\] \[k_i = \frac{1}{2}m_iv^T_{C_i}v_{C_i} + \frac{1}{2}{^iw^T_i}{^{C_i}I_i}{^iw_i}\] \[k(\Theta, \dot\Theta) = \frac{1}{2}\dot\Theta^TM(\Theta)\dot\Theta\]- $u_{ref_i}$는 위치에너지가 시작하는 기준점으로, 나중에 어차피 미분되어 사라지기 때문에 0으로 설정해도 괜찮습니다.
위 식은 사실 속도가 벡터의 형태이기 때문에 제곱을 내적으로 표현되었 뿐, $\frac{1}{2}mv^2$과 거의 동일한 식입니다.
\[\mathcal{L}(\Theta, \dot\Theta) = k(\Theta, \dot\Theta) - u(\Theta)\]위 함수를 라그랑주라고 부르는데요, 이 식에서부터 기계 시스템의 운동 에너지를 구하기 위한 라그라주 동역학 공식을 유도하는데요, 그 결과가 바로 아래의 식입니다.
\[\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial{\dot\Theta}} - \frac{\partial\mathcal{L}}{\partial{\Theta}} = \tau\] \[\frac{d}{dt}\frac{\partial k}{\partial{\dot\Theta}} - \frac{\partial k}{\partial{\Theta}} + \frac{\partial u}{\partial{\Theta}} = \tau\]- 위 식을 라그랑주 등식이라고 부릅니다.
라그랑주 역시 자코비안과 마찬가지로 할 수만 있으면, 훨씬 더 간단하고 빠르게 계산됩니다. 로봇이 잘 설계되는 경우에는 라그랑주가 쉽게 구해지지만, 모든 경우에서 잘 구해지는 것은 아니기 때문에 선택의 문제라고 할 수 있겠습니다.
직교좌표 공간에서의 머니퓰레이터 동역학
이제는 로봇 팔의 토크 뿐만 아니라 로봇 팔 손끝의 힘을 구해보겠습니다.
\[\mathcal{F} = M_{X}(\Theta)\ddot{\chi} + V_X(\Theta, \dot\Theta) + G_X(\Theta)\]이제는 말단부의 작용하는 힘에 대한 식이 되었습니다. 식의 꼴은 비슷하지만 구하려는 대상이 다르기 때문에 당연히 $M$도, $V$도, 그리고 $G$도 다를 수밖에 없는데요, 그런데 이건 자코비안을 통해 쉽게 변환할 수 있습니다.
\[\tau = J^T(\Theta)\mathcal{F}\]- $\tau$에 관한 식에 자코비안의 전치의 역을 곱해 힙에 관련된 식으로 변환할 수 있습니다.
언뜻 괜찮아 보이지만, $\ddot{\Theta}$도 남아있고 모양이 조금 맞지 않는 부분들이 있습니다. 나머지 모양까지 정리하기 위해 자코비안의 정의를 다시 살펴봅니다.
\[\dot\chi = J\dot{\Theta}\]위 식을 좌우로 미분하면 아래와 같습니다.
- $\ddot{\chi} = \dot J \dot \Theta + J \ddot \Theta$
- $\ddot \Theta = J^{-1}\ddot \chi - J^{-1}\dot J \dot \Theta$
위 두 식을 사용해 정리하면 아래와 같습니다.
\[\mathcal{F} = J^{-T}M(\Theta)J^{-1}\ddot\chi - J^{-T}M(\Theta)J^{-1}\dot J \dot \Theta + J^{-T}V(\Theta,\dot\Theta) + J^{-T}G(\Theta)\]- $M_{\chi}(\Theta) = J^{-T}(\Theta)M(\Theta)J^{-1}(\Theta)]$
- $V_\chi(\Theta, \dot\Theta) = J^{-T}(\Theta)(V(\Theta, \dot\Theta)-M(\Theta)J^{-1}(\Theta)\dot J(\Theta)\dot \Theta)$
- $G_\chi(\Theta) = J^{-T}(\Theta)G(\Theta)$
댓글남기기