로보틱스 04: 속도 기구학과 정적 힘

이 포스팅은 ‘로보틱스‘에 대한 내용을 담고 있습니다.

자료 출처: 정슬, 로봇공학, 5판, 송재복, 로봇 팔의 설계 및 제어, F. C. Park and K. M. Lynch, Introduction to Robotics, John J. Craig, Introduction to Robotics (3rd Edition), https://www.youtube.com/watch?v=O1saBbqTx5Q&list=PLP4rlEcTzeFIvgNQD8M1T7_PzxO3JNK5Z&index=11

속도 기구학

이전 포스팅에서는 각 관절과 말단부의 위치 관계에 대해서 다뤘습니다. 정기구학에서는 주어진 관절 값이 있을 때, 말단부의 위치와 자세가 어떻게 될 지에 대해서 다루었고, 역기구학에서는 반대로 말단부의 위치와 자세가 주어질 때, 각 관절을 어떻게 결정해야 하는지에 대해서 다루었습니다. 그런데 로봇 팔은 원자 속의 전자처럼 짠 하고 순간이동하는게 아니라, 시간의 지배를 받는 우리가 사는 세상 속에서 속도를 가지면서 점진적으로 이동합니다. 따라서 관절의 속도(대부분의 경우에는 각속도입니다.)에 따라 말단부의 속도가 어떻게 변하는지에 대해서 알 수 있을 것입니다. 그리고 이것을 아는 것은 꽤나 중요한데요, 기구학에서도 정확한 해가 정의되지 않는 특이점이 존재했던 것처럼 속도 기구학에서도 관절 속도가 갑자기 커지게 되는 특이점이 존재합니다. 이런 경우 로봇의 운영이 원활하지 않겠죠. 따라서 이런 경우에 어떻게 대처해야 하는지는 굉장히 중요한 문제입니다.

미소 운동(Differential Motion)

미소 운동이란 말 그대로 운동의 크기가 매우 작은 경우를 의미합니다. 즉, 방향성만 남게 되는 경우인데요, 기존의 운동과 달리 특별한 현상이 발생합니다.

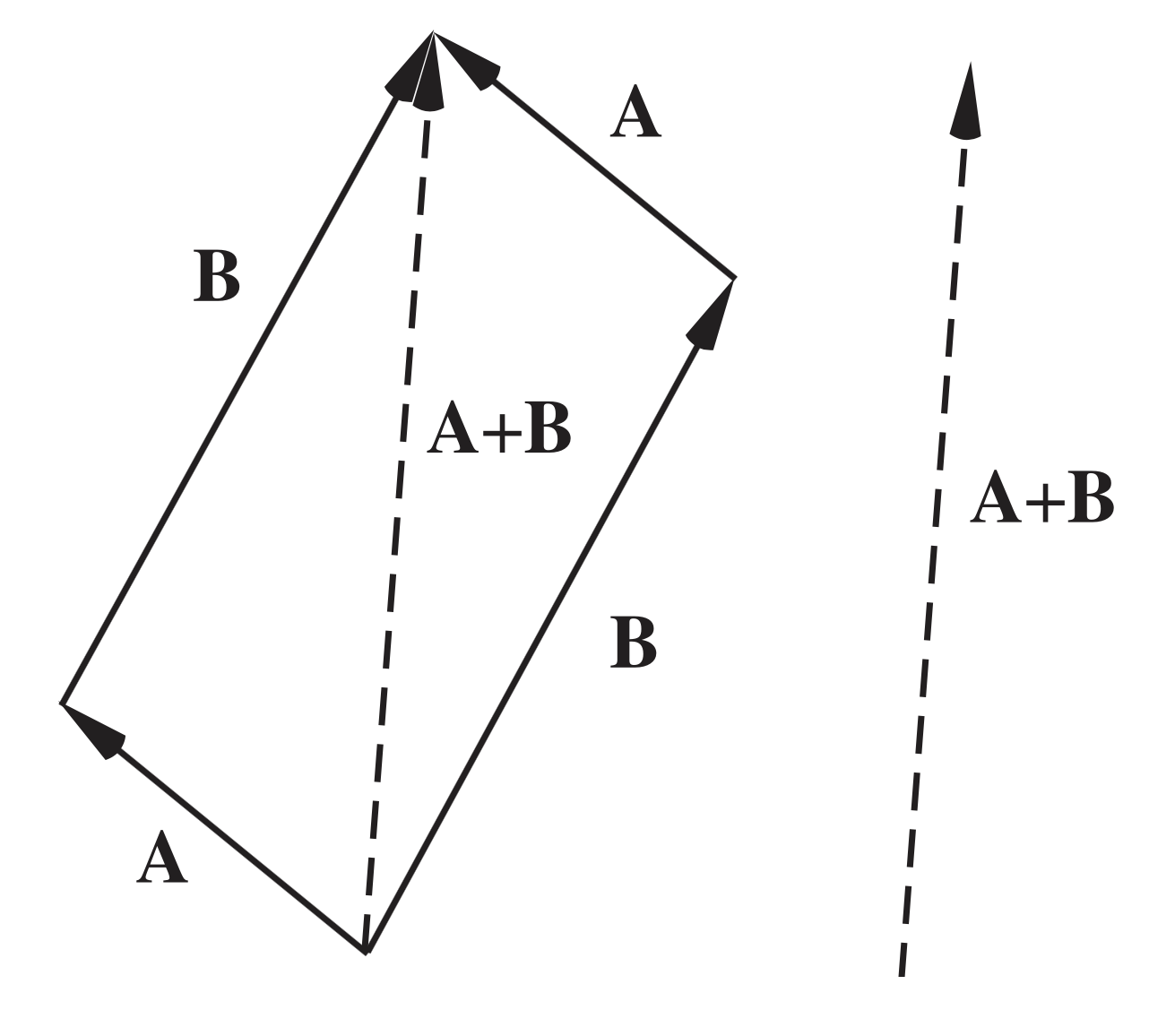
병진 운동이 나란히 있을 때, 그 순서는 결과에 어떤 영향도 끼치지 않습니다. 이것은 동차 변환 행렬으로 살펴보아도 동일한데요, 순서를 어떻게 곱해도 결과로 얻어지는 동차 변환 행렬은 동일하게 얻어집니다.

\[\begin{bmatrix} 1 & 0 & 0 & p_x \\ 0 & 1 & 0 & p_y \\ 0 & 0 & 1 & p_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & q_x\\ 0 & 1 & 0 & q_y\\ 0 & 0 & 1 & q_z\\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & q_x\\ 0 & 1 & 0 & q_y\\ 0 & 0 & 1 & q_z\\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & p_x \\ 0 & 1 & 0 & p_y \\ 0 & 0 & 1 & p_z \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & q_x + p_x \\ 0 & 1 & 0 & q_y + p_y \\ 0 & 0 & 1 & q_z + p_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

미소 병진 운동은 병진의 크기가 매우 작은 경우인데요, 아래와 같이 표현됩니다.

\[\begin{bmatrix} 1 & 0 & 0 & dp_x \\ 0 & 1 & 0 & dp_y \\ 0 & 0 & 1 & dp_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

미소 병진 운동도 마찬가지로 순서에 영향을 받지 않습니다.

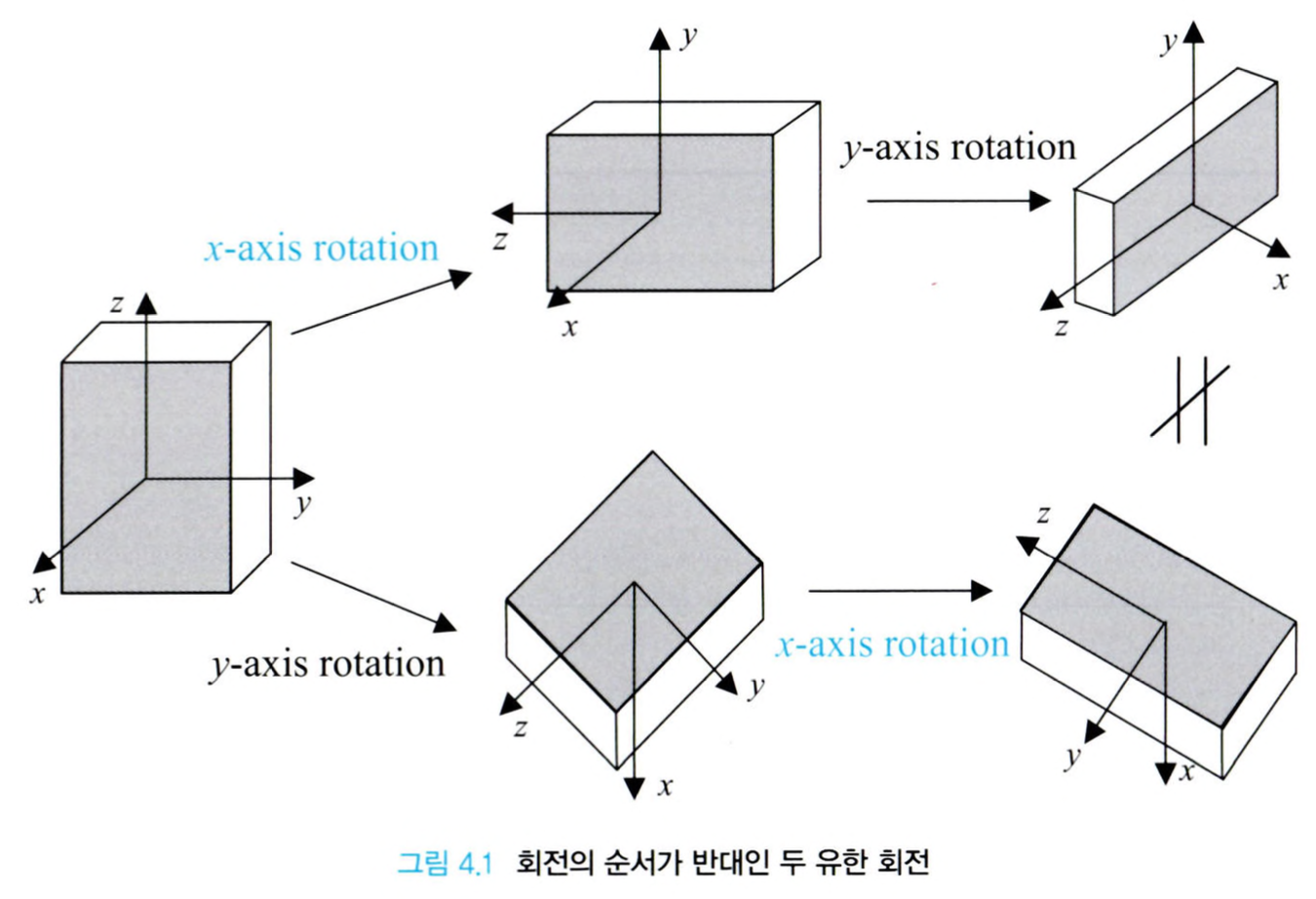
앞에서 동차 변환 행렬은 교환법칙이 성립되지 않는다고 언급한 바가 있습니다. 이는 회전행렬 때문인데요, 회전행렬은 적용되는 순서가 달라지는 경우 결과 역시 마찬가지로 달라지게 됩니다. 그런데, 미소 회전에서는 두 회전의 순서를 바꿔도 동일한 결과를 얻습니다.

\[d\phi \lt\lt 1 \rightarrow sin(d\phi) \approx d\phi \space\space \& \space\space cos(d\phi) \approx 1\] \[d\phi_xd\phi_y \approx 0\]

위 두 식은 $\phi$의 값이 작을 때, 치환할 수 있는 근삿값입니다. 위 두 식을 사용해 미소 회전 행렬을 곱해보면, 순서가 달라져도 결과가 동일함을 확인할 수 있습니다.

\[R_x(d\phi_x) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(d\phi_x) & -sin(d\phi_x) \\ 0 & sin(d\phi_x) & cos(d\phi_x) \end{bmatrix} \approx \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & -d\phi_x \\ 0 & d\phi_x & 1 \end{bmatrix}\] \[R_y(d\phi_y) \approx \begin{bmatrix} 1 & 0 & d\phi_y \\ 0 & 1 & 0 \\ -d\phi_y & 0 & 1 \end{bmatrix}\] \[R_x(d\phi_x) \cdot R_y(d\phi_y) = R_y(d\phi_y) \cdot R_x(d\phi_x) = \begin{bmatrix} 1 & 0 & d\phi_y \\ 0 & 1 & -d\phi_x \\ -d\phi_y & d\phi_x & 1 \end{bmatrix}\]

비슷하게 세 축에 대한 일반 미소 회전은 아래와 같습니다.

\[\begin{bmatrix} 1 & -(d\phi_z + d\theta_z) & (d\phi_y + d\theta_y) \\ (d\phi_z + d\theta_z) & 1 & -(d\phi_x + d\theta_x) \\ -(d\phi_y + d\theta_y) & (d\phi_x + d\theta_x) & 1 \end{bmatrix}\]

미소 회전은 직선 운동과 유사해지기 때문에, 합성의 순서가 상관 없어집니다.

속도의 표현

위치 벡터의 속도는 공간에 위치 벡터로 표시된 점의 선형 속도로 생각될 수 있는데요, 아래와 같이 표현됩니다.

\[{^BV_Q} = \frac{d}{dt}{^BQ} = \lim_{\Delta t \rightarrow 0} \frac{ {^ BQ} (t - \Delta t) - {^BQ}(t)}{\Delta t}\]

위 식은 계 ${B}$에서의 점 $Q$의 속도를 의미합니다. 만약 계${B}$에서 점의 위치가 고정되어 있다면, 속도는 0이 될 것입니다. 그런데 계${B}$ 전체가 움직이는 상황이 있을 수 있는데요, 예를 들어, 계${B}$가 계${A}$ 다음에 이어지는 관절의 좌표계일 수 있습니다. 만약 점 $Q$가 ${B}$의 관절에 고정된 툴의 좌표라면 ${B}$상에서 고정된 위치를 가지지만, 계${A}$의 관절의 동작에 따라 계${A}$에서의 위치는 달라지게 됩니다. 따라서 어떤 좌표계를 기준으로 하는 점의 위치 또는 속력인지 분명하게 명시해주어야 합니다.

${^BV_Q}$를 계${A}$에서 바라 본 속도 벡터의 표현을 아래와 같이 표현합니다.

\[^A({^BV_Q})\]

그리고 위의 식을 구하는 것은 꽤나 간단한 일입니다. 두 좌표계는 기저 벡터들의 방향도 다르고, 원점의 좌표도 다를 가능성이 큰데요, 사실 원점의 위치는 계를 변환할 때 필요한 고려 대상이 아닙니다. 우리가 신경써줘야 하는 것은 기저 벡터들이 얼마나 틀어져있는지, 그리고 그것들만을 맞춰주면 다른 계에서의 속도로 변환할 수 있고, 이 변환은 회전 행렬을 통해 쉽게 수행됩니다.

\[^A({^BV_Q}) = {^A_BR}({^BV_Q})\]

우리는 결국 기저 좌표계, 기준계상에서 로봇 팔의 끝단의 속도를 구하고 싶은건데요, 그렇기 때문에 기준계를 기준한 다른 계의 원점의 이동 속도를 아래와 같이 그리스 소문자를 사용해 특별히 다르게 표기합니다.

\[v_C = {^UV_{C \space Origin}}\]

각속도의 표현

물체의 속도에는 항상 선속도와 각속도가 동시에 존재합니다. 예를 들어, 계${A}$에서 바라 본 계${B}$ 자체의 회전을 ${^A \Omega _B}$라고 표기하고, 마찬가지로 기준계${U}$에서 바라 본 계${B}$의 각속도를 $\omega_B$라고 표기합니다.

선속도와 회전속도

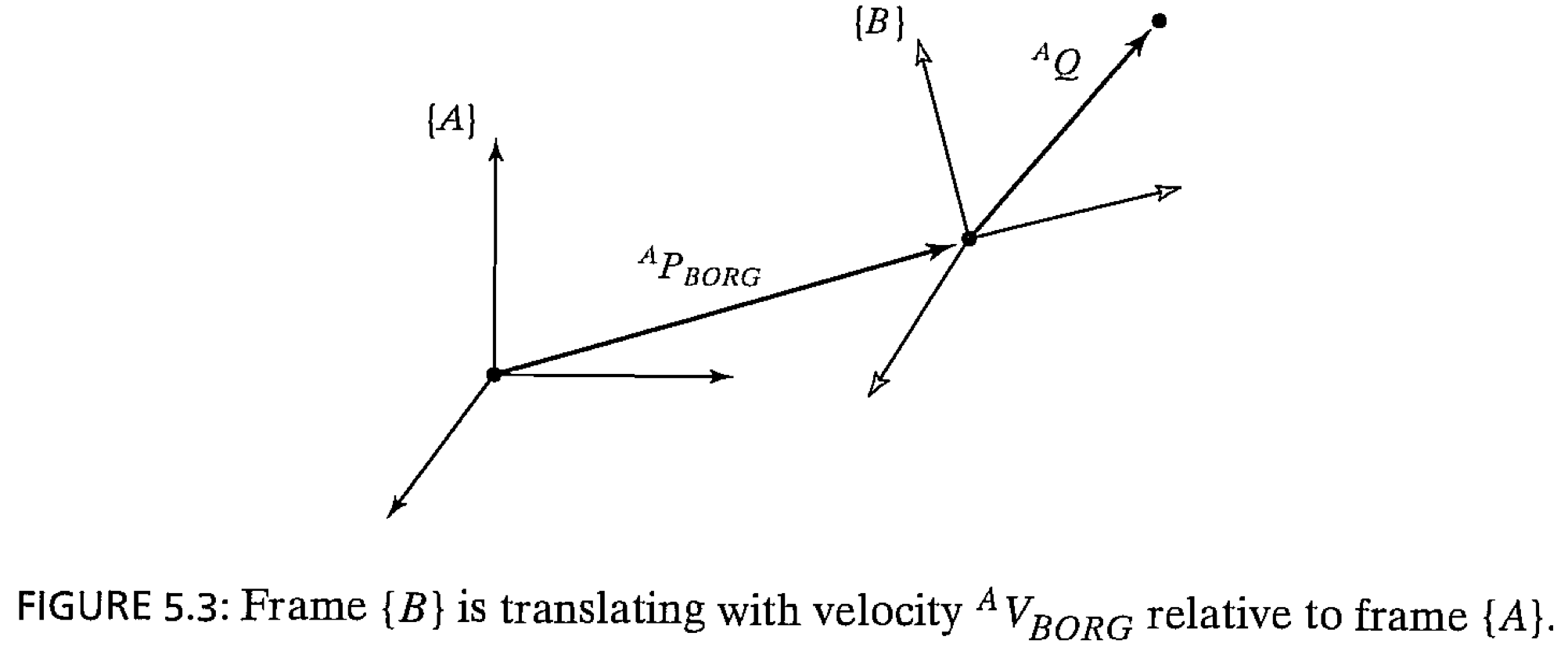
계${A}$가 있고, 계${B}$가 계${A}$상에서 움직이고 있는 상태입니다. 이때 점 $Q$가 계${B}$상에서 특정한 속도로 움직이고 있을 때, 이 속도를 계${A}$상의 속도로 바꾸는 식은 아래와 같습니다.

\[{^AV_Q} = {^AV_{B \space Origin}} + {^A_BR}{^BV_Q}\]

${^AV_{B \space Origin}}$만 추가되었는데, 이는 계의 움직임만을 의미합니다. 그런데 위 식은 상대적인 방위가 고정돼 있는 경우에만 사용할 수 있습니다. 즉, ${^A_BR}$가 시간적으로 변화하지 않는다고 가정한 경우에만 사용이 가능합니다. 계${B}$가 회전을 하는 경우에 위 식은 성립하지 않는데요, 단순히 계${B}$의 위치가 계${A}$에 대해 고정돼 있고 제자리에서 뺑글뺑글 돌아가는 점이 있는 상황만 생각해봐도 위 식은 성립하지 않습니다. 점은 분명히 회전에 의한 선속도를 가집니다. 그럼에도 위 식을 통해서 점의 속도를 구해보면 0의 값이 얻어집니다. 때문에 계 자체의 회전을 고려할 필요가 있고, 이어서 계${B}$가 회전을 하는 경우까지 설명할 수 있도록 확장합니다.

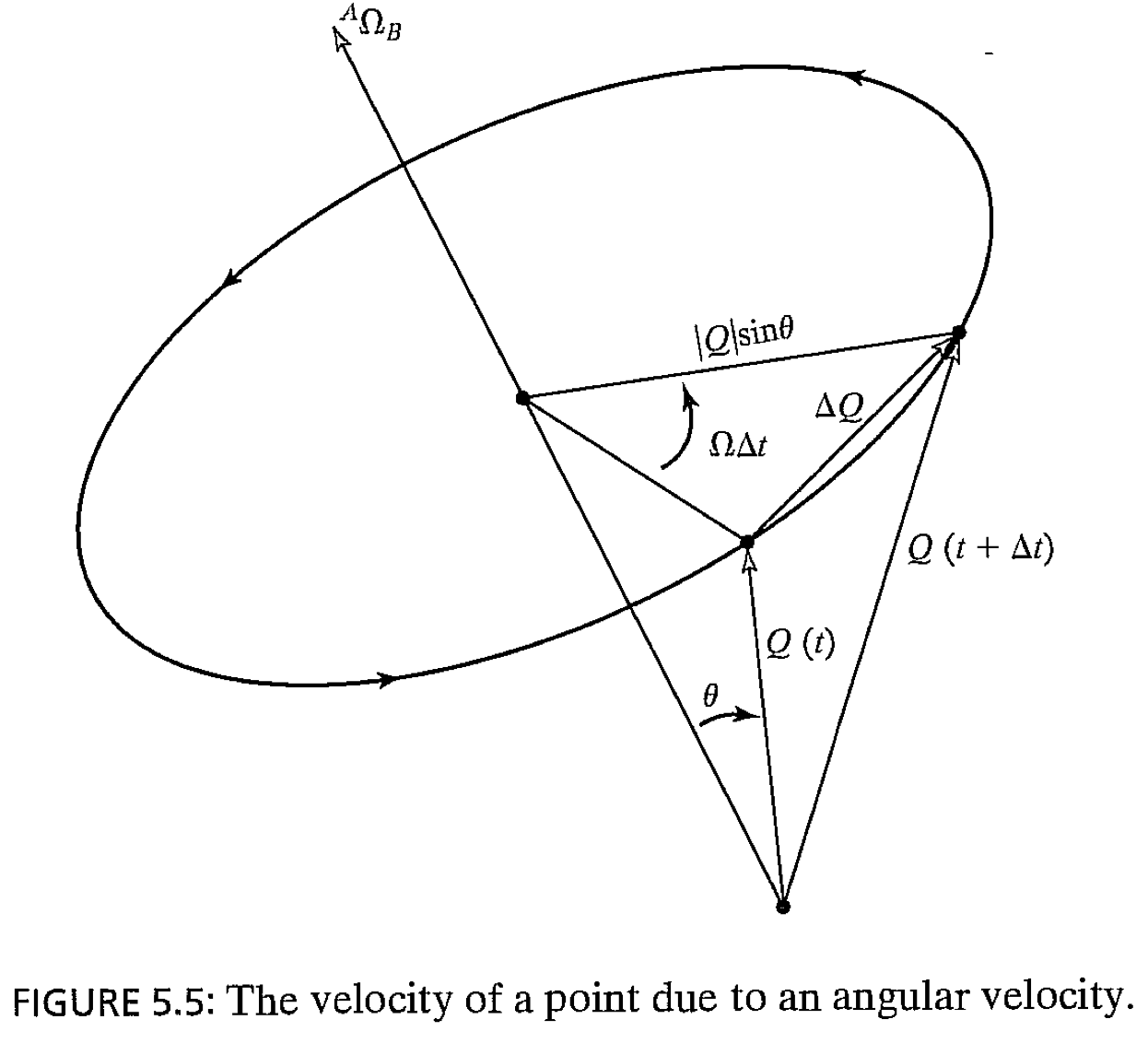
일단 계${A}$와 계${B}$의 원점이 동일하고 계${B}$가 뺑글뺑글 돌아가고 있는 간단한 상황을 살펴보겠습니다. 이 때, 각속도는 아래와 같습니다.

\[{^AV_Q}(선속도) = {^A\Omega_B}(각속도벡터)\times {^AQ}(거리)\]

위 식은 계${A}$의 관점에서 돌아가고 있는 계${B}$를 고려한 것인데요, 물체가 계${B}$에서 자체적으로 운동할 수 있다는 사실까지 고려하면 아래와 같습니다.

\[{^AV_Q} = {^A({^BV_Q})}+{^A\Omega_B}\times {^AQ}\]

회전 행렬을 드러내 좀 더 직접적으로 나타내면 아래와 같습니다.

\[{^AV_Q} = {^A_BR{^BV_Q}}+{^A\Omega_B}\times {^A_BR{^BQ}}\]

이제 계${A}$상에서의 계${B}$의 운동까지 함께 생각하면 결론적으로 아래의 식을 얻게 됩니다.

\[{^AV_Q} = {^AV_{B \space Origin}} + {^A_BR{^BV_Q}}+{^A\Omega_B}\times {^A_BR{^BQ}}\]

로봇 링크의 운동

앞에서 개념적으로 계와 계 사이의 속도 변환에 대해서 다뤘는데, 로봇의 링크에서 이것들이 어떻게 나타나는지 좀 더 직접적으로 다뤄보겠습니다.

회전관절

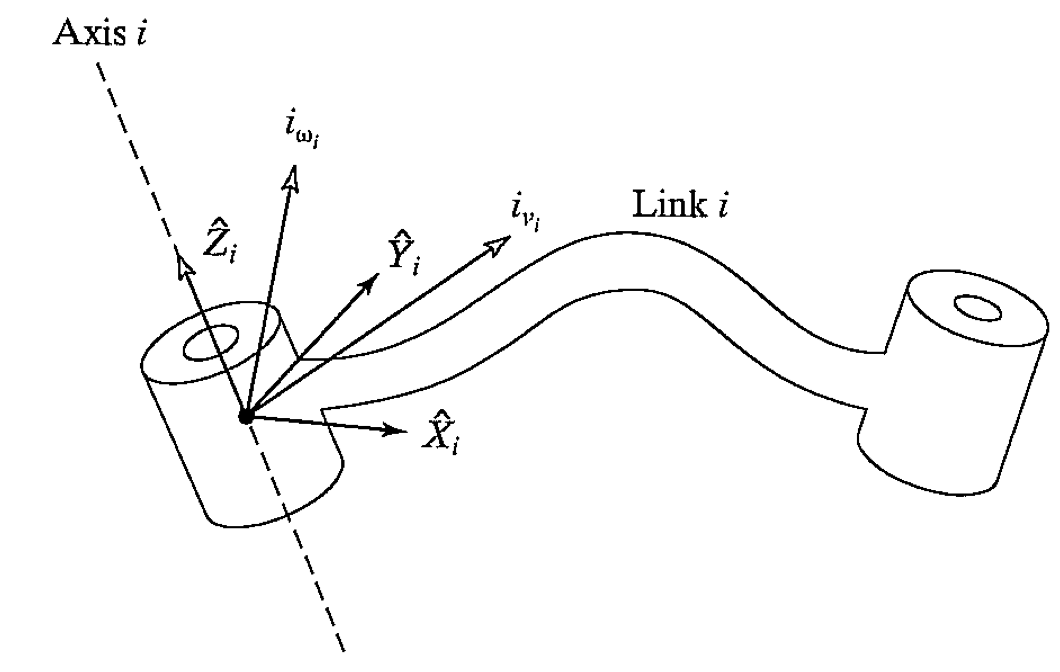
그림에서 계${i}$가 $i$번 관절 위에 설정된 것을 확인할 수 있는데요, 사실 좌표계를 설정할 때 반드시 정해진 규칙이 있는 것은 아니기 때문에 자유롭게 설정해도 괜찮습니다. 아무튼 그림에서는 계${i}$가 ${^iw_i}$의 회전속도로 움직이고 있고, ${^iv_i}$의 선속도로 움직이고 있는 것을 확인할 수 있습니다.

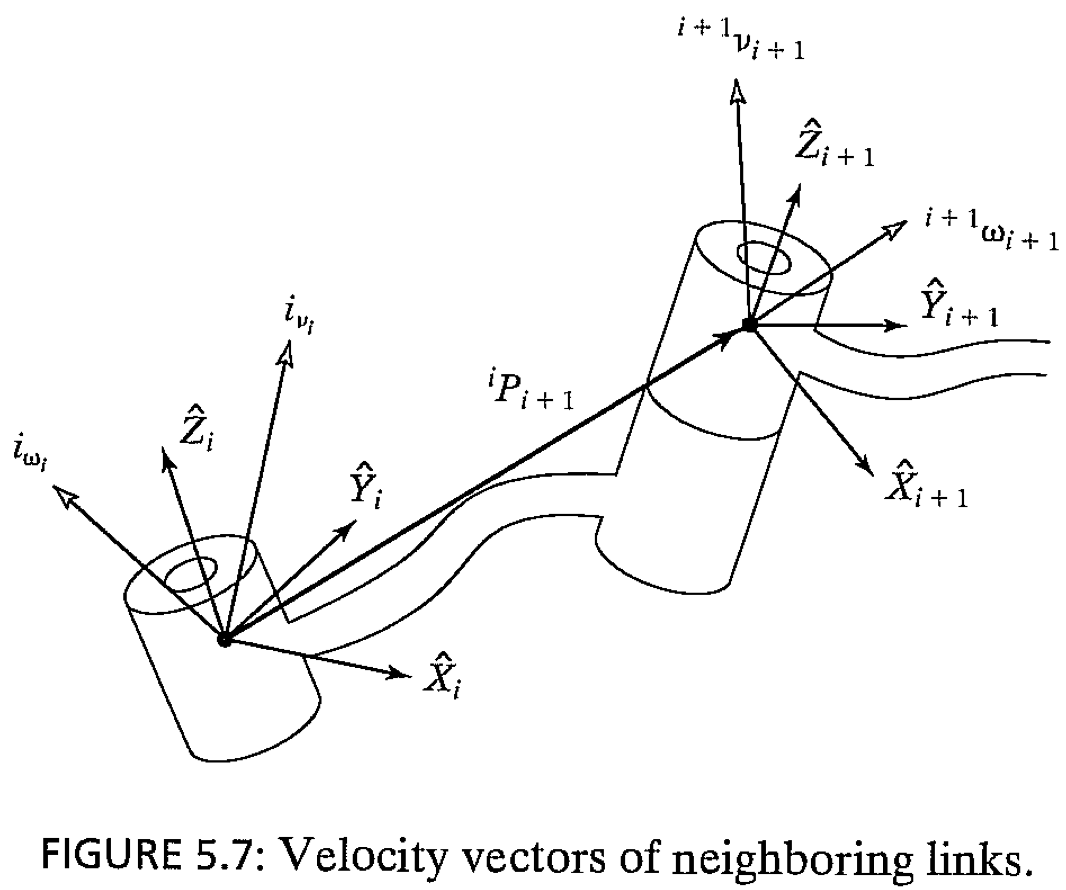
위 그림에서 계${i}$의 회전은 계${i+1}$의 속도에 직접적인 영향을 미칩니다. 계${i}$의 운동을 고려한 계${i+1}$의 각속도, 회전속도 공식은 아래와 같습니다.

\[{^{i+1}\omega_{i+1}} = {^{i+1}_iR}{^i\omega_i} + \dot{\theta}_{i+1} {^{i+1}\hat{Z}_{i+1}}\] \[\dot{\theta}_{i+1} {^{i+1}\hat{Z}_{i+1}} = {^{i+1}\begin{bmatrix} 0 \\ 0 \\ \dot{\theta}_{i+1} \end{bmatrix}}\]

위는 회전속도 공식인데요, 계${i+1}$의 회전속도는 이전 링크의 회전속도를 그대로 받게 됩니다. 그리고 계${i+1}$의 링크 자체가 돌고 있는 각속도를 추가로 더해주면 위와 같습니다. 우변의 마지막 항의 표현이 꽤나 복잡한데, 한마디로 표현하면 계${i+1}$의 각속도인데, 어차피 계${i+1}$는 $Z$축으로만 회전하기 때문에, 뒤에 ${^{i+1}\hat{Z}_{i+1}}$의 기호를 붙인 것입니다.

\[{^{i+1}v_{i+1}} = {^{i+1}_iR}({^iv_i} + {^iw_i} \times {^{i}P_{i+1}})\]

선속도 공식은 위와 같은데, 계${i}$의 선속도, 그리고 계${i}$의 회전속도로 인해 발생하는 선속도를 더해 얻은 속도를 계${i+1}$의 속도로 옮겨주는 회전변환을 곱해 얻어주게 됩니다.

프리즘 관절(직선 관절)

\[{^{i+1}\omega_{i+1}} = {^{i+1}_iR}{^i\omega_i}\]

선속도를 구하는 식이 굉장히 간단한데, 계${i+1}$이 회전운동을 하지 않기 때문에, 이전 링크의 회전운동에 관련된 부분만이 남게 됩니다.

\[{^{i+1}v_{i+1}} = {^{i+1}_iR}({^iv_i} + {^iw_i} \times {^{i}P_{i+1}}) + \dot{d}_{i+1}{^{i+1}\hat{Z}_{i+1}}\]

위 식은 선속도를 구해주는 식인데요, 계${i+1}$이 회전 관절이었을 때에는 선속도가 발생하지 않지만, 프리즘 관절인 경우에는 직선 운동이 존재하고 이를 고려해줍니다.

순차적으로 속도 전파하기

여기까지 회전 관절과 프리즘 관절에서 연쇄적으로 선속도와 회전 속도를 구해가는 방법에 대해서 배웠는데요, $\dot{\theta}$와 $\dot{d}$는 변수이고 $R$과 $P$는 변환 행렬에서 아래와 같이 구할 수 있습니다. 식에 필요한 모든 정보가 주어져 있기 때문에 식의 계산 순서에 따라가면 말단부의 속도와 각속도에 대해서 알 수 있겠습니다.

\[{^0_1T} = \begin{bmatrix} {^0_1R} & {^0_1P} \\ 0 & 1 \end{bmatrix}\]

자코비안

이제 본격적으로 관절 속도와 말단부의 속도 사이의 관계를 구해보겠습니다. 관절 속도와 말단 속도는 자코비안(Jacobian)을 통해서 직방으로 설명될 수 있습니다. 자코비안은 편미분 값들로 이루어진 행렬인데요, 말단부의 속도는 모든 관절의 속도로부터 영향을 받기 때문에 자코비안을 통해 말단부의 속도가 정의됩니다.

\[p_x = p_x(\theta_1, \theta_2)\] \[p_y = p_y(\theta_1, \theta_2)\]

말단부의 위치는 위와 같이 관절 값을 입력으로 받는 함수의 형태로 정의됩니다. 위 식을 전미분을 해 각 관절 각도의 변화에 따른 위치 변화율의 합을 표현할 수 있습니다.

\[dp_x = \frac{\partial p_x}{\partial \theta_1}d\theta_1 + \frac{\partial p_x}{\partial \theta_2}d\theta_2\] \[dp_y = \frac{\partial p_y}{\partial \theta_1}d\theta_1 + \frac{\partial p_y}{\partial \theta_2}d\theta_2\]

• 전미분 형태가 조금 낯설 수 있는데요, 직관적인 의미는 ‘관절 1에 의해 말단부가 이동하는 방향’ $\times$ ‘관절 1을 움직인 양’ $+$ ‘관절 2에 의해 말단부가 이동하는 방향’ $\times$ ‘관절 2을 움직인 양’ 입니다.

\[\begin{bmatrix} d p_x \\ d p_y \end{bmatrix} = \begin{bmatrix} \frac{\partial p_x}{\partial \theta_1} & \frac{\partial p_x}{\partial \theta_2} \\ \frac{\partial p_y}{\partial \theta_1} & \frac{\partial p_y}{\partial \theta_2} \end{bmatrix} \begin{bmatrix} d \theta_1 \\ d \theta_2 \end{bmatrix}\] \[d\vec{x} = J(\theta)d\vec{\theta}\]

위 식은 관절 각도의 움직임에 따른 말단부 움직임의 변화량이기 때문에 아직 속도가 아닙니다. 따라서 양 변을 시간으로 미분해주면, 결론적으로 말단 속도와 관절 속도 사이의 관계를 구할 수 있습니다.

\[\frac{d\vec{x}}{dt} = J(\theta)\frac{d\vec{\theta}}{dt}\] \[\dot{x} = J(\theta)\dot{\theta}\]

• 문자 위의 점은 시간에 대한 미분을 의미합니다.

• 위 식의 표기법에서 $\vec{x} = \begin{bmatrix} p_x & p_y \end{bmatrix}^T$ 이므로, $\dot{x} = \begin{bmatrix} \dot{p_x} & \dot{p_y} \end{bmatrix}^T = \begin{bmatrix} v_x & v_y \end{bmatrix}^T$입니다(표기법 혼동 주의).

위의 식을 통해 이제 $p$가 어떠한 모습이든지 주어지기만 한다면, 관절 속도와 말단부 속도의 관계를 구할 수 있습니다. 그러면 말단부의 속도에는 어떤 것들이 있을까요? 바로 생각나는 속도는 각 축방향으로의 선속도입니다. 예를 들어, 2차원 평면이라고 한다면 $x$축 방향 속도와 $y$축 방향 속도가 있습니다. 그런데 2차원 평면에서 말단부의 속도라고 하면 선속도일 수도 있지만, 사실 각속도도 있습니다. 여기에서 각속도는 기저 좌표계(${0}$)를 기준으로 합니다.

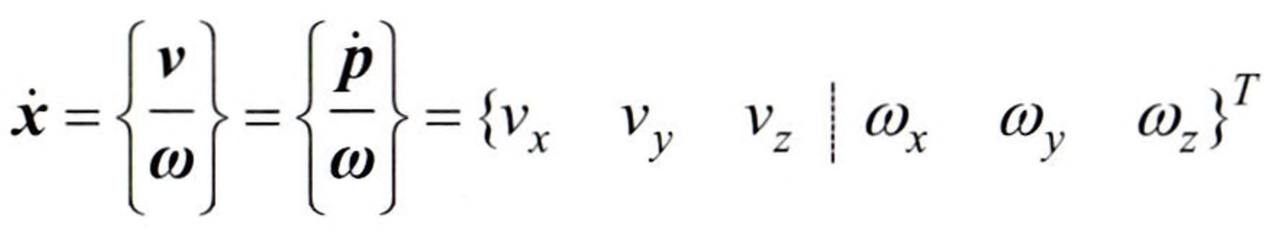
위와 같이 말단부의 속도 집합이 설정될 때, $J$를 기하학적 자코비안(Geometric Jacobian)이라고 합니다. 말단부의 위치, 그리고 말단부가 기저 좌표계의 원점과 이루는 각도를 관절 변수로 표현한 식이 주어지면, 이 식을 통해 자코비안 행렬을 구할 수 있고, 곧 속도를 구할 수 있게 됩니다.

• PUMA 560의 자코비안 유도: https://www.youtube.com/watch?v=nwj0xR21ldo

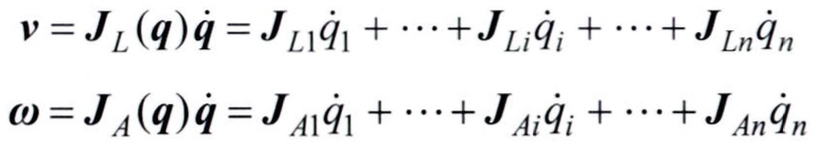
정리하면 위와 같은데요, 위 식에서 $J_{L1}$, $J_{L2}$, … 들의 크기는 $(3 \times 1)$입니다. $J_{Li}$에서도, $J_{Ai}$에서도 마찬가지로 각 축($x$, $y$, $z$)으로의 방향을 의미합니다. 그런데, 기하학적 자코비안에는 치명적인 문제점이 있는데요, 그건 바로 적분을 했을 때 실제 방위가 얻어지지 않을 수 있다는 점입니다.

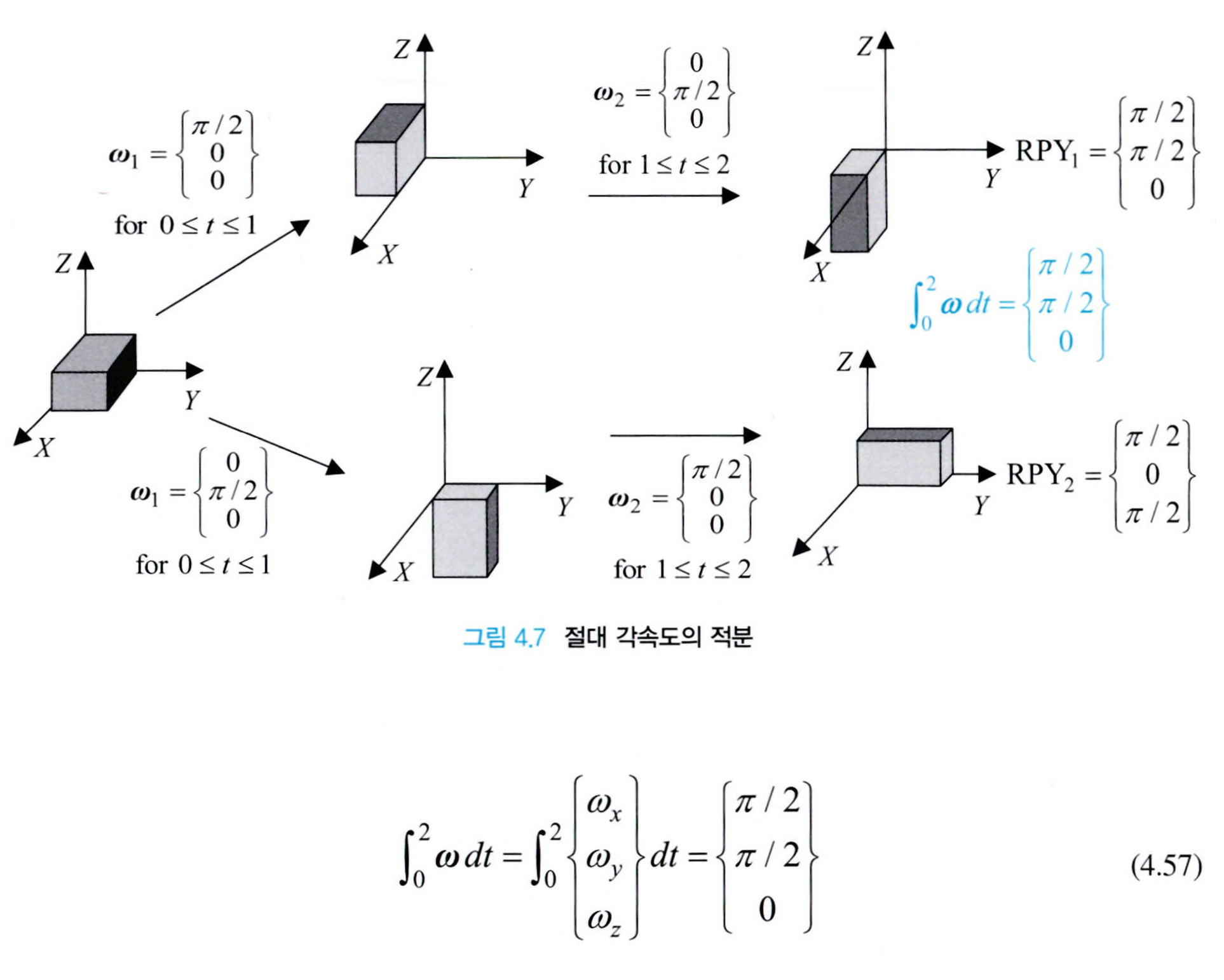
위 그림에서 로봇의 말단부가 $x$축과 $y$축을 따라서 $\pi/2$만큼 회전하는데, 먼저 회전하는 축의 순서를 달리하면, 결과 방위가 달라지는 것을 확인할 수 있습니다. 만약 로봇이 $y$축 방향으로 먼저 회전했다면, 적분 결과와는 분명하게 다른 방위를 가지게 됩니다. 이런 결과가 발생하는 이유는 로봇의 회전 변환에 내제된 다른 축들과의 종속성 때문인데요, 이런 문제점들을 해결하기 위해 해석학적 자코비안(Analytical Jacobian)이 사용됩니다. 해석학적 자코비안에서는 오일럭 각도를 사용하는데, 오일러 각도를 사용하면 각속도를 시간에 따라 적분하면 올바른 방위를 얻어낼 수 있습니다.

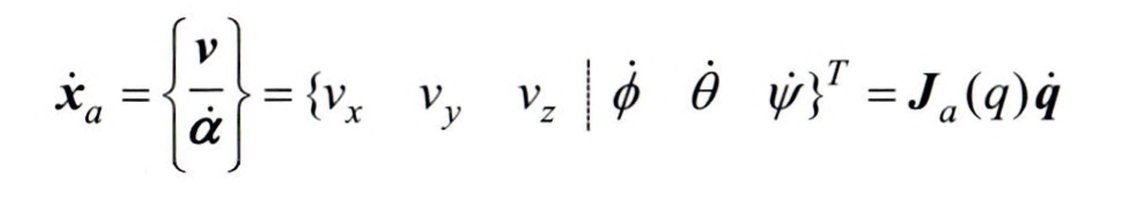
자코비안이 한 번 구해지면, 다른 계로 변환하는 것은 굉장히 단순한 일입니다. 두 계 사이의 회전 행렬만 알고 있으면 바로 다른 계에서의 자코비안 행렬을 얻어낼 수 있습니다.

\[\begin{bmatrix} {^Av} \\ {^A\omega} \end{bmatrix} = \begin{bmatrix} {^A_BR} & 0 \\ 0 & {^A_BR} \\ \end{bmatrix} \begin{bmatrix} {^Bv} \\ {^B\omega} \end{bmatrix}\] \[{^AJ(\Theta)}\dot{\Theta} = \begin{bmatrix} {^A_BR} & 0 \\ 0 & {^A_BR} \\ \end{bmatrix} {^BJ(\Theta)}\dot{\Theta}\] \[{^AJ(\Theta)} = \begin{bmatrix} {^A_BR} & 0 \\ 0 & {^A_BR} \\ \end{bmatrix} {^BJ(\Theta)}\]

특정 위치에서의 자코비안 구하기

특정 위치의 자코비안을 구하는 것은 생각보다 쉬운 일입니다. 위의 식에서 우리에게 주어지지 않은 값은 없기 때문에 식의 요구에 따라 대입만 해주면, 자코비안을 얻어낼 수 있습니다. 하지만, 위의 방식은 특정 위치에서의 자코비안만을 구할 수 있을 뿐, 모든 위치에 대한 전체적인 설명을 제공하지는 못합니다.

특이성(Singularity)

자코비안 행렬을 통해 로봇의 말단부를 제어할 수 있습니다. 하지만 실제로는 말단부의 속도와 각속도가 이만큼이어야 할 때, 각 관절속도는 어떻게 되어야 하는지, 즉, 자코비안의 역행렬이 훨씬 더 자주 필요합니다. 그리고 자코비안 행렬의 역행력이 역시 존재하지 않을 수 있는데요, 이를 기구의 특이성이라고 부릅니다. 수학적으로 자코비안이 구해지지 않는다는 사실은 해당 위치에서 로봇이 요구한 속력과 각속도를 만들어낼 수 없음을 의미합니다. 때문에 로봇이 특이 지점은 보통 기구학적인 한계로 인해 로봇의 말단부가 도달할 수 없는 구역, 그리고 로봇이 팔을 최대로 뻗은 상태(선속도를 내기에 굉장히 불리함)에서 발생합니다.

• 작업 공간 경계에서의 특이성(Workspace Boundary Singularities)
• 작업 공간 내부의 특이성(Workspace Interior Singularities)

특이성을 확인하는 과정은 크게 어렵지 않은데요, 특정 행력의 역행렬이 존재하지 않는 것은 행렬식의 값이 0이 되기 때문인데요, 즉, 행렬식의 값이 0이 되는 공간을 사전에 계산해 기구의 특이성을 파악할 수 있습니다.

머니퓰레이터 내부에서의 정적 힘(Static Foces)

자코비안을 통해 속도 기구학을 쉽게 할 수 있었습니다. 그런데 자코비안 행렬을 알면 머니퓰레이터의 정적 힘을 손쉽게 구할 수 있습니다. 정적 힘이란 고정된 자세에서 꾸준이 누르는 힘, 예를 들면 팔을 쭉 피고 있는 상태로 물건을 들고 있는 경우가 해당됩니다. 물건을 들고 이리저리 휘두르는 것은 동적 힘으로 다음 포스팅에서 다룹니다. 그런데 사실 우리가 팔을 쭉 피고 있으면 힘을 주지 않는 것이 아니죠. 우리의 세계에는 중력이 존재하기 때문에 팔을 움직일 때 중력을 이기기 위한 힘을 꾸준히 가해야 되는데, 로봇 팔도 예외는 아닙니다. 그러나 여기에서는 보다 단순한 상황에서 먼저 살펴보기 위해 중력이 링크에 가하는 힘은 고려하지 않습니다.

\[{^if_i} - {^if_{i+1}} = 0\] \[{^in_i} - {^in_{i+1}} - {^iP_{i+1}} \times {^if_{i+1}} = 0\]

위 두 식은 링크에 가해지는 정적 힘과 좌표계 ${i}$를 중심으로 하는 토크의 합이 0일 때 성립되는 식입니다. 링크는 고정된 위치에 유지되기 때문에 두 힘은 동일한 값을 가집니다. 토크는 조금 복잡한데요, 단순히 토크 끼리만이 동일한 것이 아니라, 좌표계 ${i+1}$에 가해지는 정적 힘(${^if_{i+1}}$)에 의해 발생하는 토크까지 함께 고려해서 ${i}$와 ${i+1}$가 동일한 토크를 가집니다. 이제 좌표계를 자신에게 맞게 바꿔주기만 하면 아래의 식을 얻을 수 있습니다.

\[{^if_i} = {^i_{i+1}R} {^{i+1}f_{i+1}}\] \[{^in_i} = {^i_{i+1}R} {^{i+1}n_{i+1}} + {^iP_{i+1}} \times {^if_{i}}\]

근데 우리는 어차피 $Z$축에 대해서만 힘을 가할 수 있었습니다(회전이든 프리즘이든 운동 축, 방향을 $Z$로 설정하기 때문). 때문에 관절 액추에이터의 토크는 아래와 같습니다.

• 회전형 관절 액추에이터의 토크

  \[\tau_i = {^in_i}^T {^i\hat{Z}_i}\]

• 미끄럼형 관절 액추에이터의 토크

  \[\tau_i = {^if_i}^T {^i\hat{Z}_i}\]

정적 힘을 구하기 위한 연쇄 식은 선속도를 구하기 위한 식과 순서가 반대입니다. 때문에 우리가 말단부에서 가하고자 하는 힘의 양이 있으면, 그냥 거기에서부터 출발해서 모든 관절이 가져야하는 토크의 양을 구할 수 있습니다.

\[\tau = \begin{bmatrix} l_1s_2 & l_2+l_1c_2 \\ 0 & l_2 \\ \end{bmatrix} \begin{bmatrix} f_x \\ f_y \end{bmatrix}\] \[J(\Theta) = \begin{bmatrix} l_1s_2 & 0 \\ l_1c_2 + l_2 & l_2 \end{bmatrix}\]

식을 보고 알 수 있는 사실은, 토크를 구하기 위해 필요한 식이 자코비안이 전치된 형태라는 것입니다. 때문에 자코비안이 미리 알려져 있으면, 이를 전치해서 우리에게 필요한 각 관절의 토크 값을 바로 얻어낼 수 있습니다.

속도와 정적 힘의 직교좌표계 변환

지금까지 속도와 정적 힘에 대해서 다루었는데, 마지막으로 속도와 정적 힘의 좌표계 변환에 대해서 살펴봅니다. 사실 지금까지 계의 변환을 계속 해왔기 때문에 새로운 내용은 아닌데요, 이전에 계속 사용했던 식을 살펴보겠습니다.

\[{^{i+1}v_{i+1}} = {^{i+1}_iR}({^iv_i} + {^iw_i} \times {^{i}P_{i+1}})\] \[{^{i+1}\omega_{i+1}} = {^{i+1}_iR}{^i\omega_i} + \dot{\theta}_{i+1} {^{i+1}\hat{Z}_{i+1}}\]

위 수식은 회전관절의 계 변환 공식인데요, 위 식에서 $i+1$을 $B$로, $i$를 $A$로 바꾸고 행렬을 사용해 정리하면 아래와 같습니다.

\[\begin{bmatrix} {^Bv_B} \\ {^B\omega_B} \end{bmatrix} = \begin{bmatrix} {^B_AR} & -{^B_AR}{^AP_{B \space Origin}} \times \\ 0 & {^B_AR} \\ \end{bmatrix} \begin{bmatrix} {^Av_A} \\ {^A\omega_A} \end{bmatrix}\]

• 위 식에서 $\dot{\theta}_{i+1}$는 0으로 가정됩니다.

위 식의 역을 구하면 아래와 같습니다.

\[\begin{bmatrix} {^Av_A} \\ {^A\omega_A} \end{bmatrix} = \begin{bmatrix} {^A_BR} & {^AP_{B \space Origin}} \times {^A_BR}\\ 0 & {^A_BR} \\ \end{bmatrix} \begin{bmatrix} {^Bv_B} \\ {^B\omega_B} \end{bmatrix}\]

마찬가지로 힘에 대해서도 동일한 작업을 해보면 아래와 같습니다.

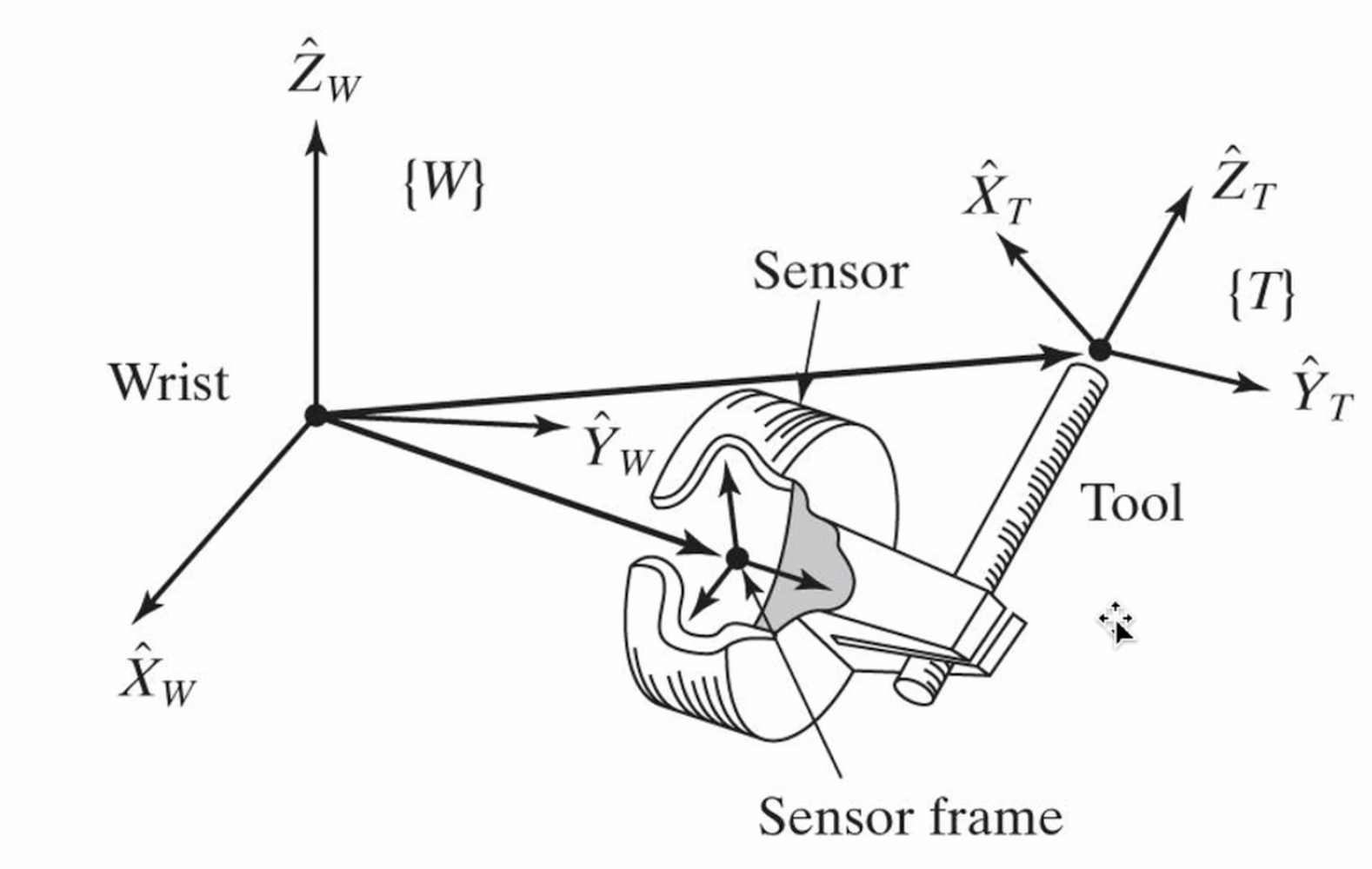
\[\begin{bmatrix} {^AF_A} \\ {^AN_A} \end{bmatrix} = \begin{bmatrix} {^A_BR} & 0\\ {^AP_{B \space Origin}} \times {^A_BR} & {^A_BR} \\ \end{bmatrix} \begin{bmatrix} {^BF_B} \\ {^BN_B} \end{bmatrix}\]

재미있는 사실은 여기에서도 마찬가지로 전치행렬의 관계를 가진다는 점입니다. 즉, ${^A_BT_f} = {^A_BT_v}^T$의 관계가 성립합니다. 이걸 도대체 어떤 상황에서 사용할까 싶은데요, 아래 사진과 같은 경우에 유용하게 사용됩니다. 만약에 로봇팔의 끝에 도구를 잡고 있고, 이걸로 무언가를 누르는 일을 하는 상황을 생각해 보겠습니다. 이 경우 우리가 관심있는 정보는 로봇이 도구로 벽면을 얼마만큼의 힘으로 누르고 있는지 인데요, 도구 끝에 센서를 설치하는 것은 항상 가능한 일이 아니기 때문에 대부분의 경우에는 손목부에 센서가 설치됩니다. 이때, 힘에 대한 변환행렬을 사용해 손목에서 측정한 힘을 도구 끝 좌표계 상의 힘으로 변환할 수 있습니다.