로보틱스 03: 기구학(역기구학)

이 포스팅은 ‘로보틱스‘에 대한 내용을 담고 있습니다.

자료 출처: 정슬, 로봇공학, 5판, 송재복, 로봇 팔의 설계 및 제어, F. C. Park and K. M. Lynch, Introduction to Robotics

로봇 기구학(역기구학)

로봇 작업의 대부분은 사실 역기구학 해가 없어도 수행할 수 있습니다. 하지만 직교 공간상에서 말단 자세가 주어지는 경우에는 역기구학 해를 구해야만 로봇이 원하는 자세로 이동하는 것이 가능합니다.

정밀도와 정확도

정확도와 반복 정밀도의 차이에 대해 잘 아는 것이 중요합니다. 정확도란 로봇을 여러 번 제어할 때, 그 평균 값이 실제 원하는 곳과 얼마나 가까운가를 의미합니다. 평균의 값이 얼마나 가까운가가 측정 대상이기 때문에 점들의 분포는 중요하지 않습니다. 반복 정밀도란 로봇을 반복 제어할 때 점들이 얼마나 서로 가까운가를 의미합니다. 실제로 원하는 곳과 가까운지와는 관련이 없습니다. 인공지능에서 Bias와 Variation과 비슷하게 대응되는 개념입니다.

정확도와 반복 정밀도는 로봇을 제어하는 방식에 따라 중요성이 다른데요, 이 포스팅에서 다룰 역기구학을 통해 로봇을 제어하는 경우 정확도가 중요합니다. 역기구학은 직교공간상에 말단부의 위치와 자세를 주고 그에 따라 로봇 팔의 관절을 조절해 말단부를 요구되는 위치와 자세로 맞추는 작업인데요, 당연히 원하는 위치와 자세로 움직이게 하는게 목표기 때문에 실제 정답과 비슷한가가 중요합니다.

로봇 팔을 제어하는 다른 방법도 존재하는데, 대표적으로는 교시-재현(Teach and Playback) 방법이 있습니다. 이 방법은 작업자가 직접 로봇의 관절과 말단부를 잡아 끌고 원하는 자세를 지정합니다. 로봇 팔은 작업자가 지정한 관절값을 저장하고 반복합니다. 작업자가 정답 위치와 자세를 알려주기 때문에 정확성 보다는 반복 정밀도가 중요한 항목이 됩니다.

역기구학

각 관절의 해를 역으로 구하는 문제인 역기구학은 연산 능력의 향상으로 인해, 야코비안에 기반한 속도 제어 방식을 채택하면 역기구학 해가 없어도 로봇의 위치 제어가 가능해졌습니다. 그리고 모델 기반의 토크 제어 방식을 채택하면, 말단 자세를 달성하기 위한 각 관절 모터의 토크가 직접 산출되기 때문에 역기구학 문제를 해결할 필요가 사라집니다(아직 다루지 않은 내용). 그럼에도 역기구학의 해를 사용하면 훨씬 간단한 계산을 통해 제어를 할 수 있기 때문에 가급적이면 역기구학 해가 존재할 수 있도록 설계하는 것이 바람직합니다.

해로 주어지는 위치와 자세는 각각 자유도를 3만큼 가지기 때문에 총 6개의 방정식을 얻을 수 있습니다. 따라서 로봇 팔이 6 이상의 자유도를 가질 때 로봇은 닫힌 해를 1개 이상 얻게 됩니다(작업 공간 내부에서). 그런데 로봇 팔의 자유도가 6 이상이라고 무조건 닫힌 해를 다 가질 수 있는 것은 아닌데요, 당연하게도 로봇 팔을 이상하게 만들어놓으면, 관절 개수가 6개가 넘는다고 해도 모든 작업 공간에서 닫힌 해를 가질 수 없을 것입니다.

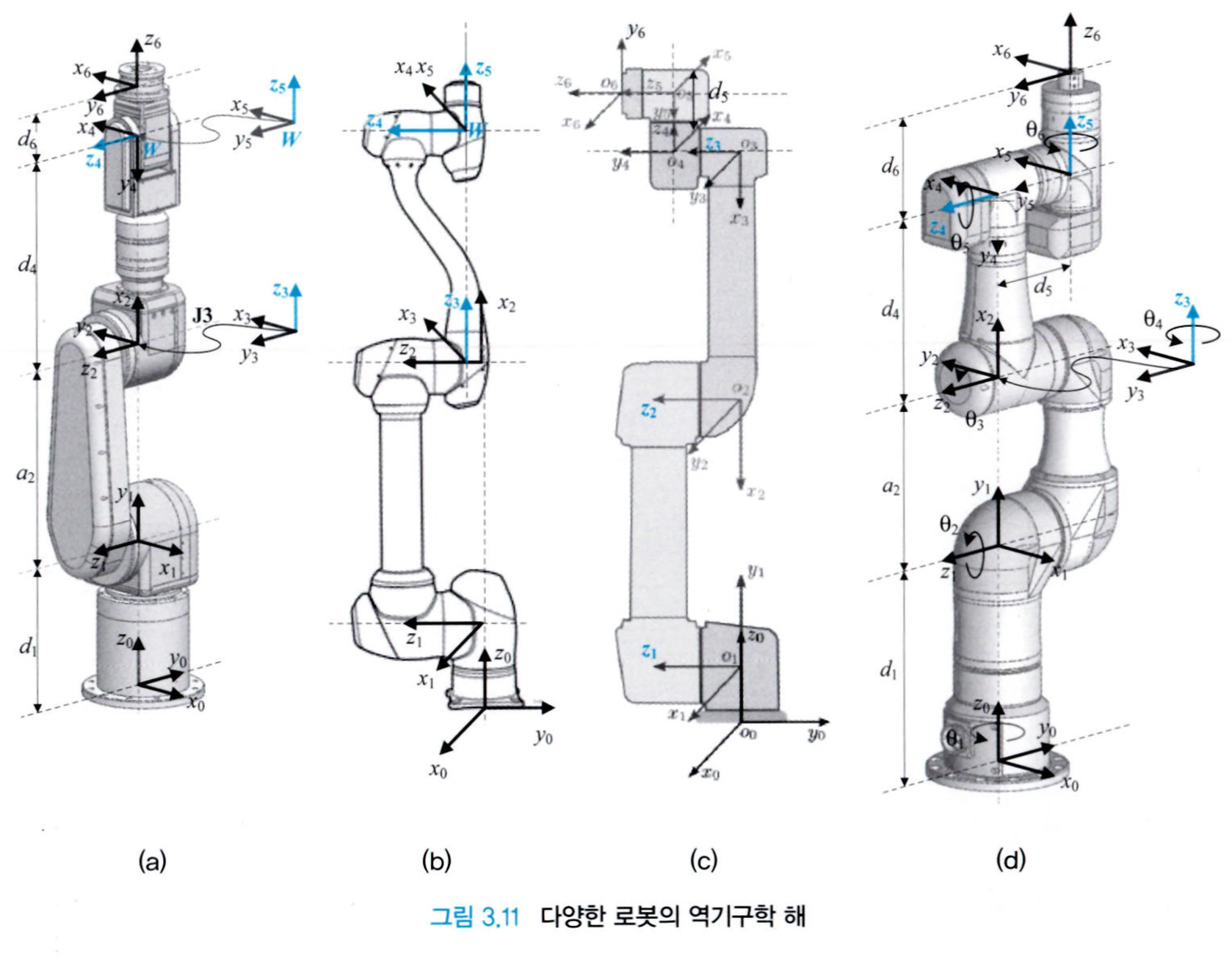
로봇 팔이 닫힌 해를 가지기 위해서는 아래의 두 가지 조건 중 하나 이상을 만족해야 합니다.

• 3개의 연속되는 회전 관절의 관절 축이 한 점에서 교차하는 경우

• 3개의 연속되는 회전 관절의 관절 축이 평행하는 경우

  위 그림의 (a), (b)는 첫 번째 경우를 만족합니다. 그리고 (c)는 두 번째 경우를 만족합니다. 따라서 (a), (b), (c)는 닫힌 해를 가지게 됩니다. 그러나 (d)의 경우는 어떤 경우에도 해당되지 않기 때문에 닫힌 해를 가지지 못합니다.

  로봇 팔의 정기구학 표현식은 복잡한 삼각함수들의 곱으로 이루어지는데요, 때문에 역기구학의 해를 구하는 과정은 매우 복잡합니다. 하지만 위의 조건을 만족한다면 로봇 팔은 작업 공간 내의 가능한 위치와 자세에 대해 유일 해(Unique Solution)를 가집니다. 당연히 작업 공간 내에 있다고 해서 모든 자세가 가능한 것은 아닙니다. 만약에 로봇이 팔을 쭉 피고 간신히 도달할 수 있는 위치일 때, 손이 뒤를 돌아보게 하는것은 거의 대부분의 로봇 팔에서 불가능한 동작입니다. 이런 영역의 차이를 구분하는 용어가 있는데요, 말단부가 어떤 방위로든 도달할 수 있는 공간을 자유자재(Dextrous) 작업 영역이라고 하고, 최소 1개의 방위로 도달할 수 있는 공간, 그러니까 어떻게든 닿을 수 있는 공간을 도달가능(Reachable) 작업 영역이라고 부릅니다.

여기에서 유일 해는 단일 해를 의미하는게 아닌데요, 유일 해는 단일 해일 수도 있고, 유한한 다중 해일 수도 있습니다. 여러 가지 해를 구했다면, 그 중에서 장애물을 회피해 도달할 수 있는 해를 선택하는 것이 바람직하겠습니다.

PUMA의 역기구학

6 자유도의 PUMA 로봇 팔(R(Role) - P(Pitch) - P - R - P - R)은 손목부의 관절 축이 손목 부에서 교차하기 때문에 닫힌 해를 구할 수 있습니다. 그리고 손목부에 위치한 세 관절은 손목점에 대해서 회전하기 때문에 말단부의 위치에 영향을 주지 않습니다. 따라서 역기구학 해를 구할 때, 몸체부와 손목부를 기구학적으로 분리(Kinematic Decoupling)해 다루게 됩니다.

몸체부의 역기구학

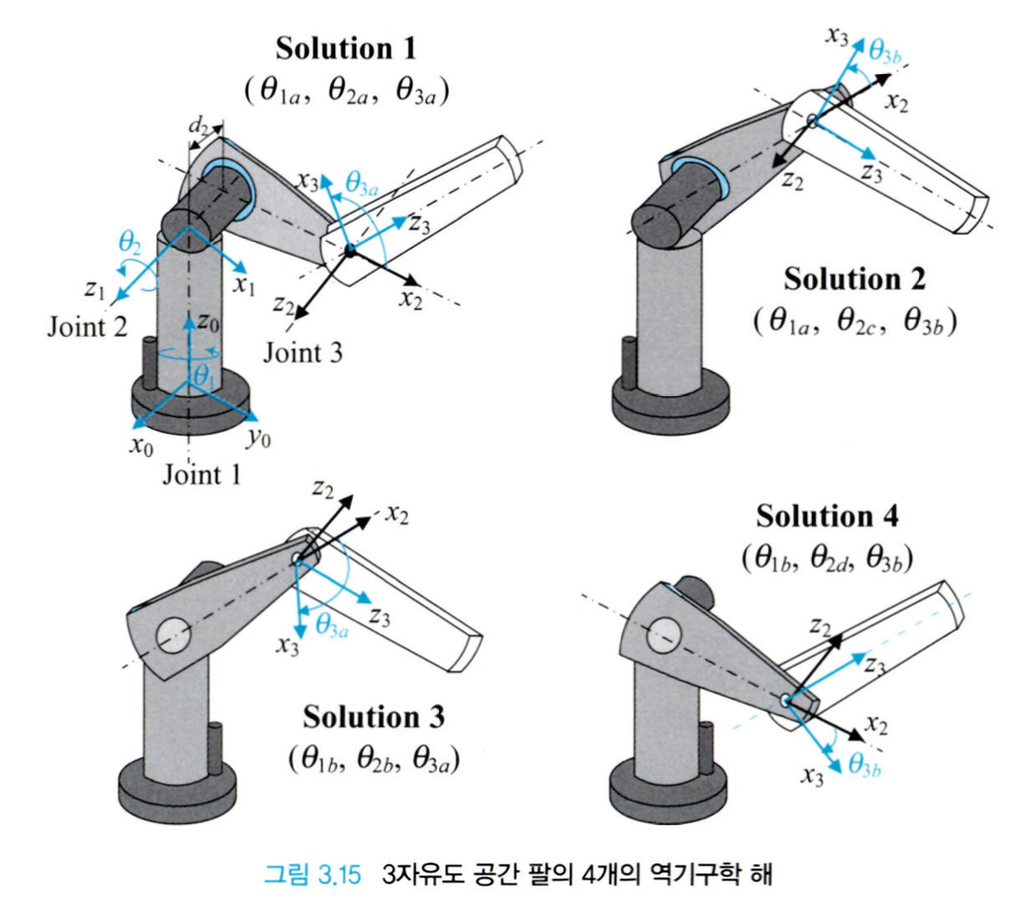
3자유도 공간 팔의 경우 위의 해를 가집니다. 1번 관절이 앞을 보는지, 혹은 뒤를 보는지에 따라, 그리고 상향 팔꿈치 자세인지, 하향 팔꿈치 자세인지의 조합을 통해 총 4개의 해를 가지게 됩니다.

손목부의 역기구학

손목부 역시 마찬가지로 총 2개의 해를 가집니다. 손목부에서는 특이하게 해가 무수히 존재하는 경우가 발생하는데요(몸체부도 가장 꼭대기의 경우 해가 무수히 존재함), 이는 로보틱스 첫 번째 포스팅에서 다룬 오일러 각도 표현의 짐벌 락이 발생하는 이유와 동일합니다. 때문에 오일러 각에서와 동일하게 4, 5, 6번 관절의 중간 관절인 5번 관절의 각도에 따라 무한 해의 여부가 결정됩니다.

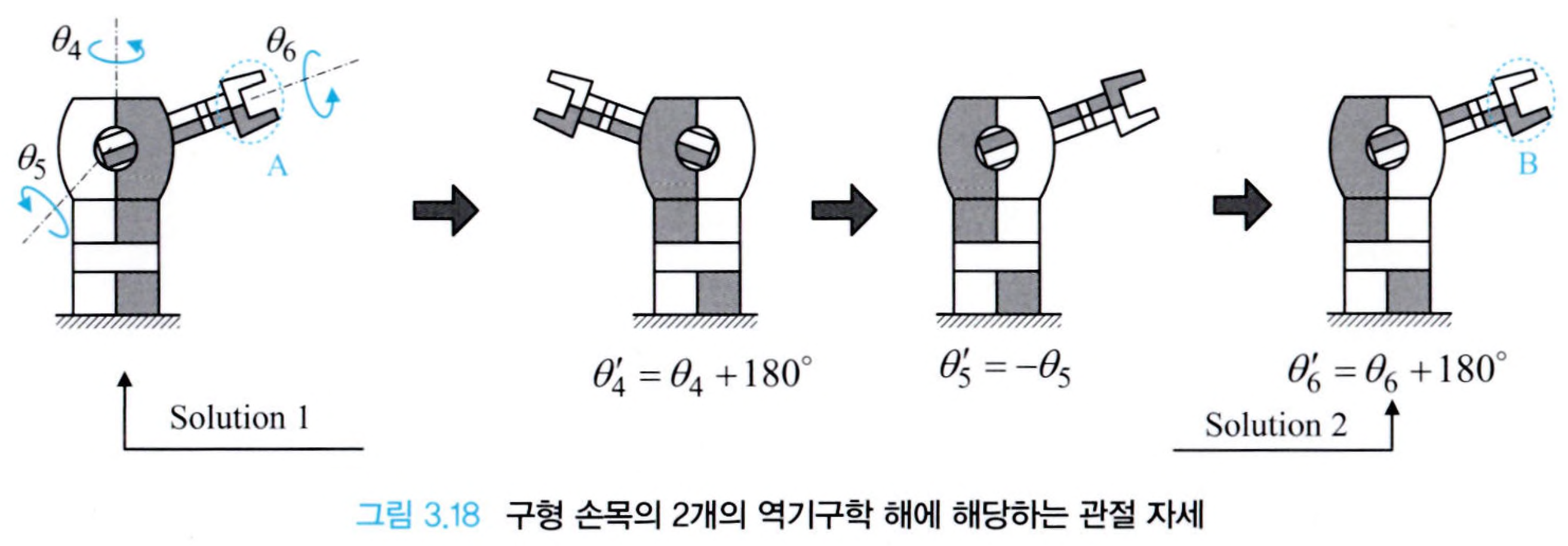
짐벌 락에 해당하지 않는 경우 위의 그림과 같이 2개의 해를 가집니다.

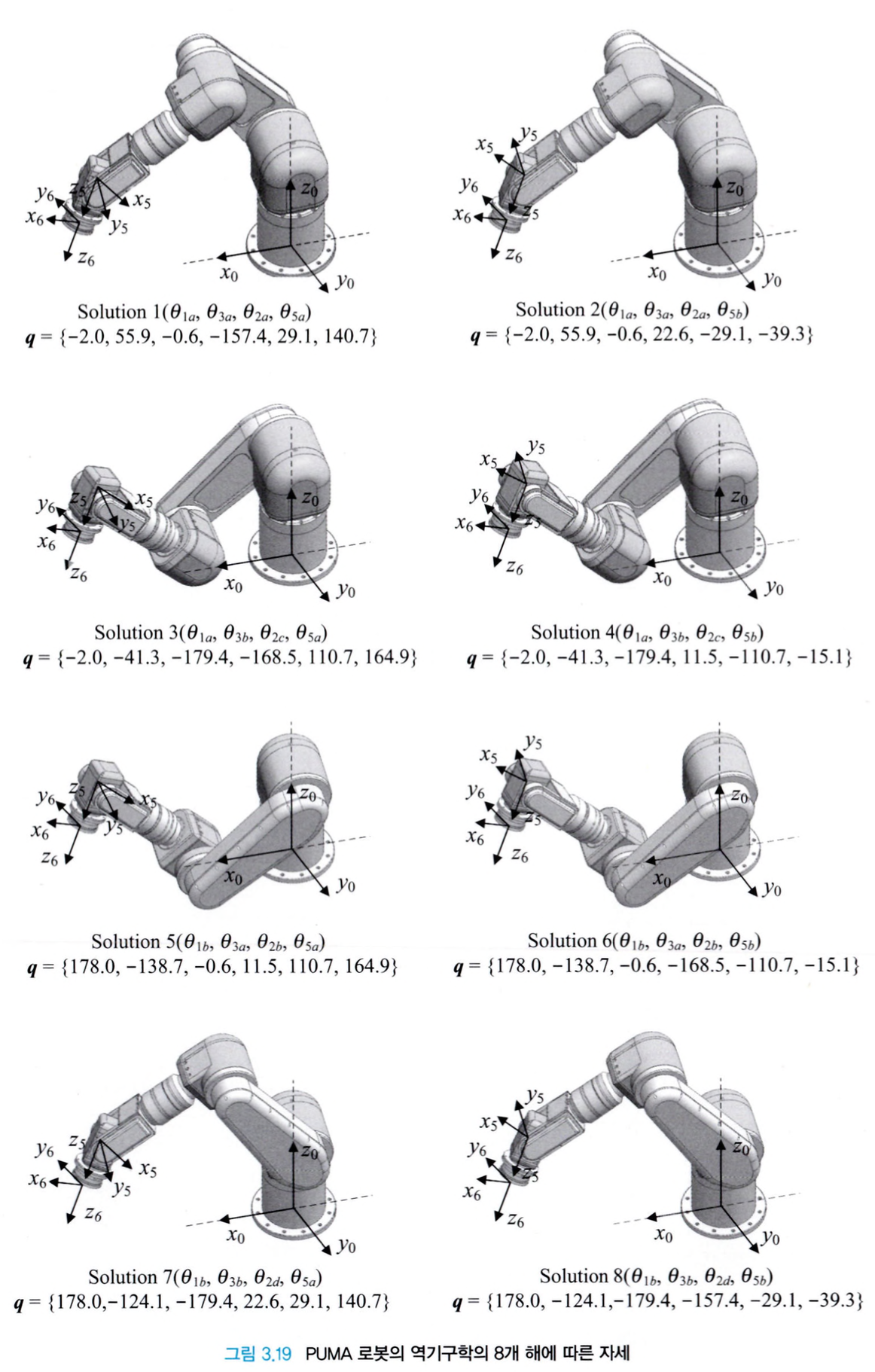
그리고 결론적으로는 위와 같이 총 8개의 다중 해를 가집니다.