5 분 소요

글에 들어가기 앞서…

이 포스팅은 ‘로보틱스‘에 대한 내용을 담고 있습니다.

자료 출처: 정슬, 로봇공학, 5판, 송재복, 로봇 팔의 설계 및 제어, F. C. Park and K. M. Lynch, Introduction to Robotics

로봇 기구학

기구학(Kinematics)는 로봇을 구성하는 링크의 위치, 속도, 가속도, 시간 간의 관계를 해석하는 분야입니다. 기구학에서는 로봇 운동의 원인이 되는 힘에 대해서는 다루지 않습니다. 기구학은 크게 관절 공간의 변수를 통해 말단부의 자세를 구하는 정기구학과 말단부의 자세에서 관절 공간의 변수를 구해내는 역기구학으로 구분됩니다. 아래 내용에서 자세히 살펴봅니다.

Denavit-Hartenberg 표현

D-H(Denavit-Hartenberg) 표현방식은 서로 인접한 좌표의 회전, 전이 관계를 나타냅니다. Translation 행렬은 인접한 링크의 좌표계 사이의 전이 관계를 나타내는데요, 기본 전역 좌표로부터 이 Translation 행렬을 계속 곱해나가면, end-effector까지의 관계를 구할 수 있습니다

.

\[P_0 = T_0^nP_n\]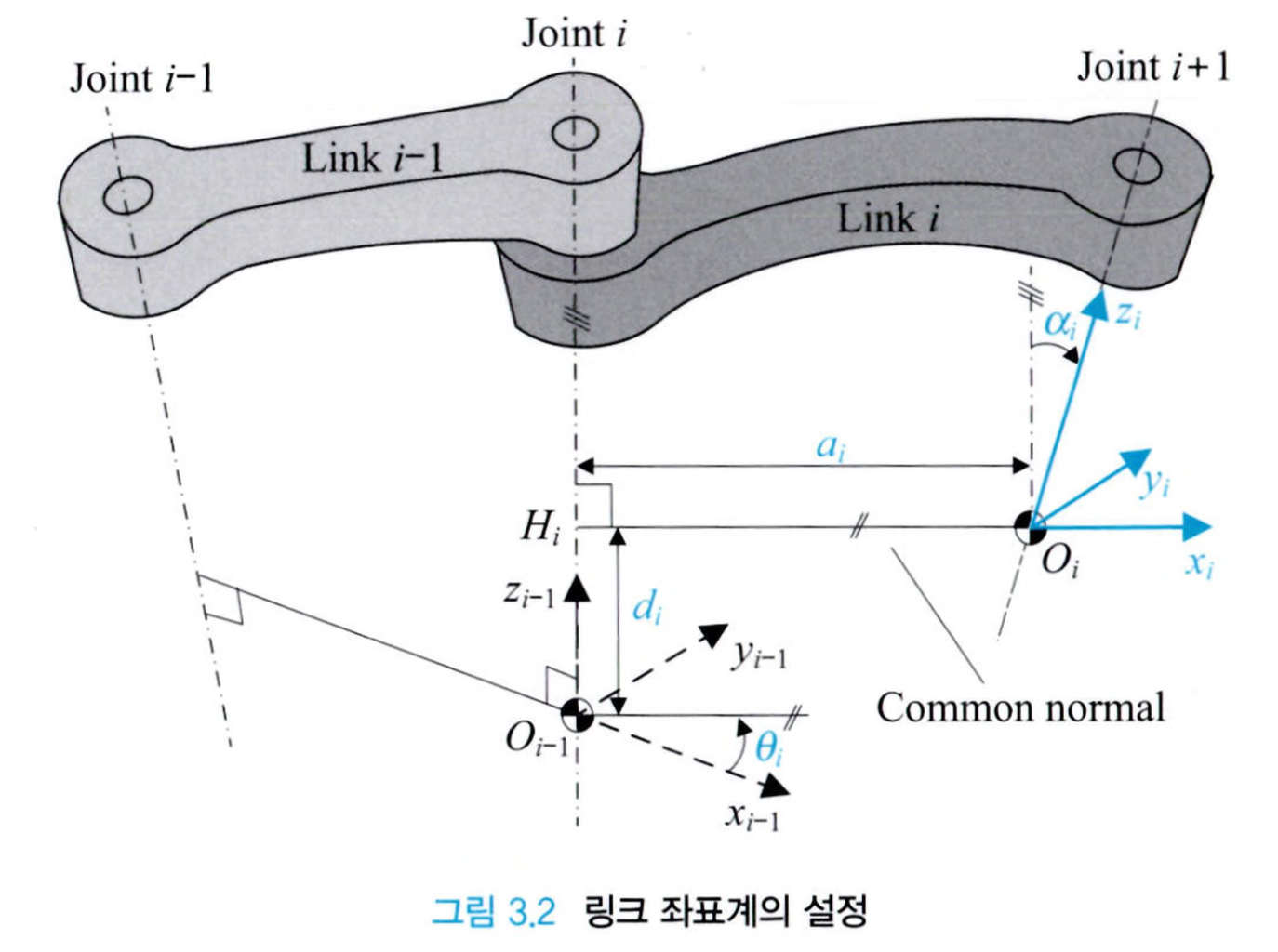

image-20241027143753448

이 Translation 매트릭스에 2개의 DH 구속 조건을 추가하면 단 4개의 변수만으로 링크 간의 관계를 정의할 수 있습니다(원래는 6개의 변수로 표현하기 때문에 2개가 줄어 4개).

  1. $x_i$축은 $z_{i-1}$축과 수직이다.
  2. $x_i$축은 $z_{i-1}$축과 교차한다.

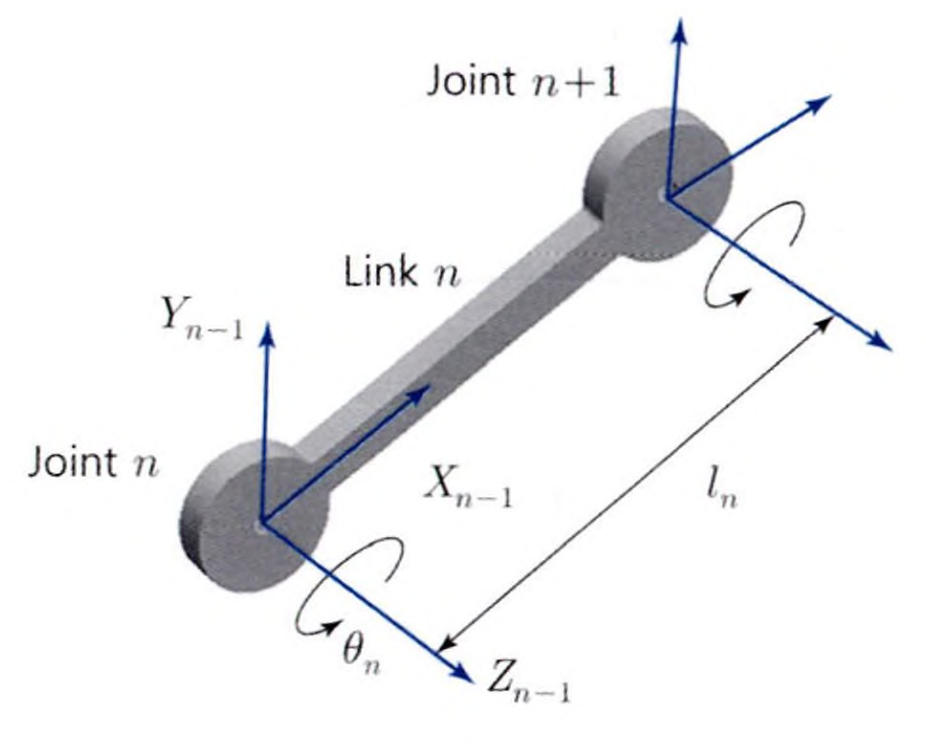
위의 그림과 같이 DH 구속 조건을 만족하도록 좌표계가 설정되면 오직 4개의 변수만으로 링크 사이의 관계를 표현할 수 있고, 그림의 파란색 글씨로 나타난 $a_i$, $\alpha_i$, $d_i$, $\theta_i$가 바로 그 변수들인데, 이들을 DH 파라미터라고 부릅니다.

DH 좌표계 표기법 종류

먼저 좌표계를 위치하는 방식이 조금 특이합니다. 좌표계를 설정하는 방법에는 크게 2가지가 있습니다.

  1. 표준 DH 표기법: 원위 관절에 좌표계의 원점을 설정
  2. 수정 DH 표기법: 근위 관절에 좌표계의 원점을 설정

근위 관절과 원위 관절은 하나의 링크를 사이에 둔 두 관절의 관계를 표현하는 용어인데요, 근위 관절은 말 그대로 기저부에 더 가까운 관절을 의미하고, 원위 관절은 기저부로부터 먼, 말단부에 가까운 관절을 의미합니다. 용어 자체만으로는 왠지 수정 DH 표기법이 더 많이 사용될 것 같은데요, 실제로는 그렇지 않습니다. 표준 DH 표기법을 훨씬 더 많이 사용하며, 제가 참고한 로봇공학과 로봇팔의 설계 및 제어 교재 둘 다 표준 DH 표기법을 기준으로 설명합니다. 관절의 인덱스와 좌표축의 인덱스가 일치하지 않는데, 이 부분을 각별히 주의해야 합니다.

z축의 설정

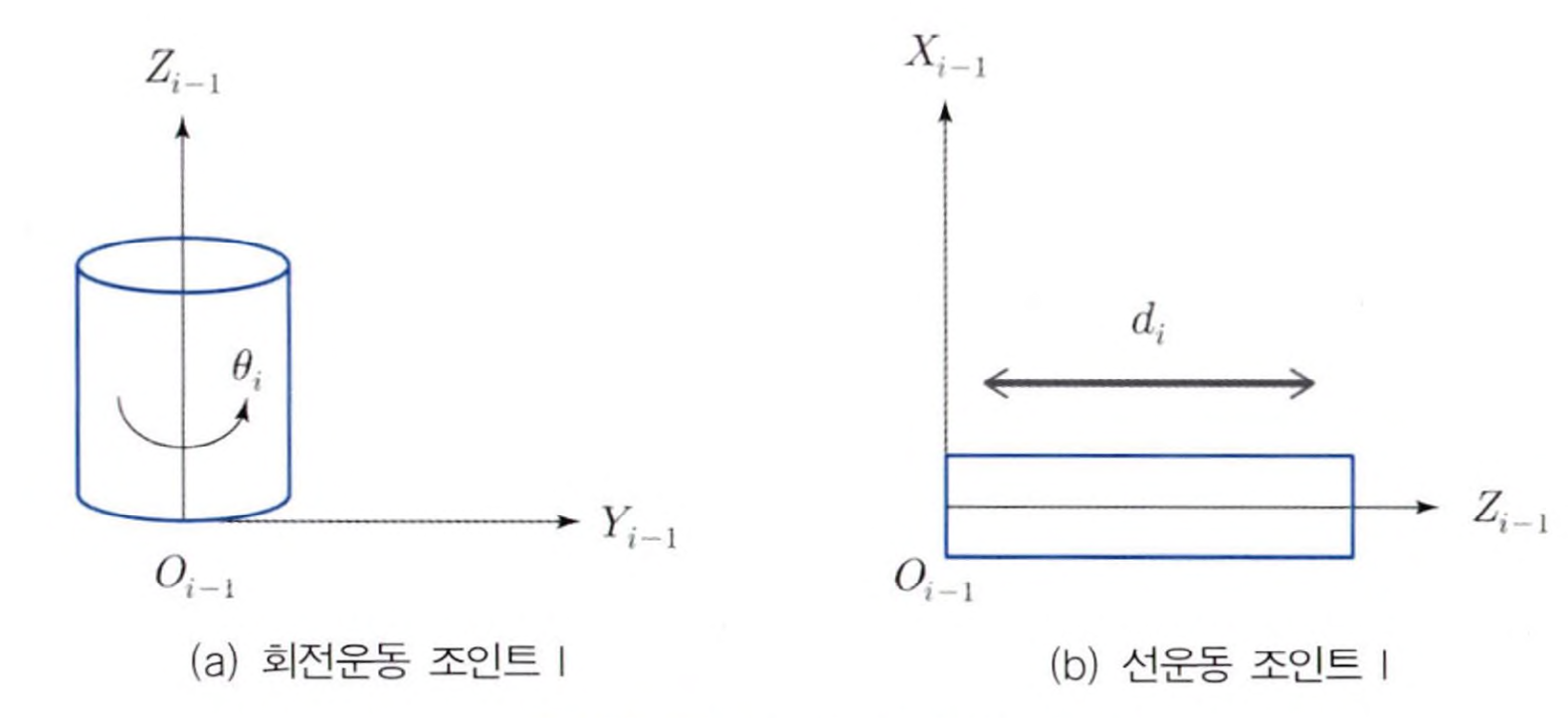
image-20241027144903066

좌표계의 $z$축은 위의 그림과 같이 회전관절의 경우 회전하는 축을 $z$축으로 설정하고, 선운동 관절의 경우 운동하는 방향을 $z$축으로 설정합니다.

원점의 설정

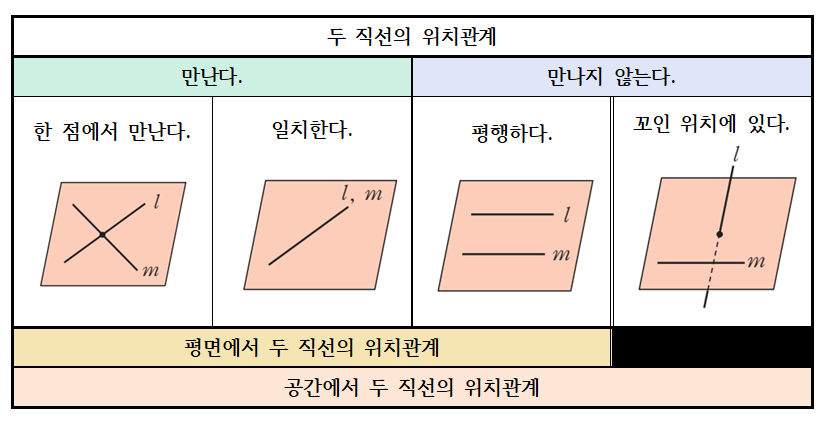
두 직선의 위치관계 정리

로봇을 구성하는 관절의 생김새는 굉장히 다양한데, 이를 기하학적으로는 3가지로 분류할 수 있습니다. 기하학적으로 분류하는 기준은 링크를 사이에 둔 좌표계들의 $z$축의 위치관계입니다. 공간에서 두 직선의 위치관계는 위와 같이 총 4가지 이지만, 여기에서는 만나는 경우를 한 가지 경우로 간주하고 아래의 3가지 경우로 나누어 생각합니다.

  1. 두 관절 축이 동일한 평면상에 위치하지 않음(꼬인 위치)
  2. 두 관절 축이 동일한 평면상에 위치하고, 서로 만나지 않음(평행)
  3. 두 관절 축이 교차, 또는 일치함

두 관절 축에 모두 수직인 직선을 공통 법선이라고 합니다. 1번 경우에는 공통 법선이 유일하게 존재하고, 2번 경우에서는 무한한 공통 법선이 존재합니다. 마지막으로 3번 경우에서는 직선이 자체로 교차하기 만나기 때문에 법선이 존재하지 않습니다.

  1. 두 관절 축이 동일한 평면상에 위치하지 않는 경우

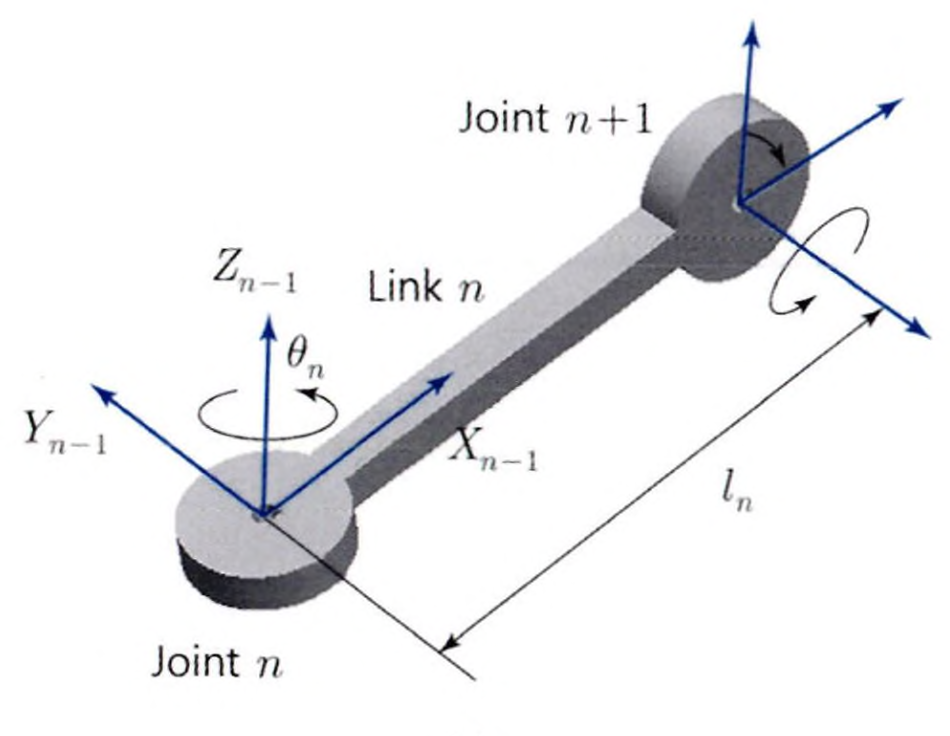
image-20241027153030467

공통 법선과 관절 축 $i+1$의 교점에 원점을 설정합니다. 관절 축 $i+1$은 곧 $z_i$인데요, 다르게 말하면 현재 설정하고자 하는 좌표계의 $z$축인 $z_i$축과 공통 법선의 교점을 원점으로 설정합니다.

  1. 두 관절 축이 동일한 평면상에 위치하고 서로 만나지 않는 경우

image-20241027154616559

평행하는 경우 역시 마찬가지 인데요, 여기에서 발생하는 문제점은 공통 법선이 하나로 결정되지 않는다는 점입니다. 이 때, 우리는 이전 좌표계의 원점을 사용합니다. 이전 좌표계의 원점을 지나는 공통 법선과 $z_i$축과 만나는 지점을 원점으로 설정합니다.

  1. 두 관절 축이 교차, 또는 일치하는 경우

두 관절 축이 교차하는 경우에는 공통법선이라는게 아예 존재하지 않는데요, 이 경우에는 교점 자체를 원점으로 설정합니다.

x축, y축의 설정

원점을 설정할 때 사용한 공통 법선의 연장선상에 $x$축을 설정합니다. 단, 방향은 이전 좌표계에서 나가는 방향으로 설정해야 합니다. 이어서 $y$축은 링크 좌표계가 우수 직교 좌표계가 되도록 결정합니다.

DH 파라미터

위에서 좌표계를 설정하면 해당 좌표계와 이전 좌표계의 관계를 표현하는 동차 변환 행렬을 구할 수 있습니다. 그런데, 우리가 좌표계를 설정할 때 DH 구속 조건을 만족하도록 좌표계를 설정했기 때문에 단 4개의 변수만으로 동차 변환 행렬을 표현할 수 있습니다.

image-20241027160705714

  • $a$(링크 길이): 두 관절이 얼마나 떨어져 있는지를 의미합니다. 두 관절 축의 거리인 $x_i$축 상의 길이가 곧 링크이기 때문에, 링크 길이라고 표현합니다.
  • $\alpha$(링크 비틀림): 두 관절을 $x_i$축과 수직인 평면에 사영했을 때 이루는 각도를 의미합니다.
  • $d$(관절 오프셋, 거리): 이전 링크 좌표계의 $z_{i-1}$축을 기준으로 이전 링크 좌표계와 현재 링크 좌표계의 $x$축 사이의 거리를 의미합니다.
  • $\theta$(관절 각도): 이전 링크 좌표계의 $z_{i-1}$축을 기준으로 이전 링크 좌표계와 현재 링크 좌표계의 $x$축 사이의 각도를 의미합니다.

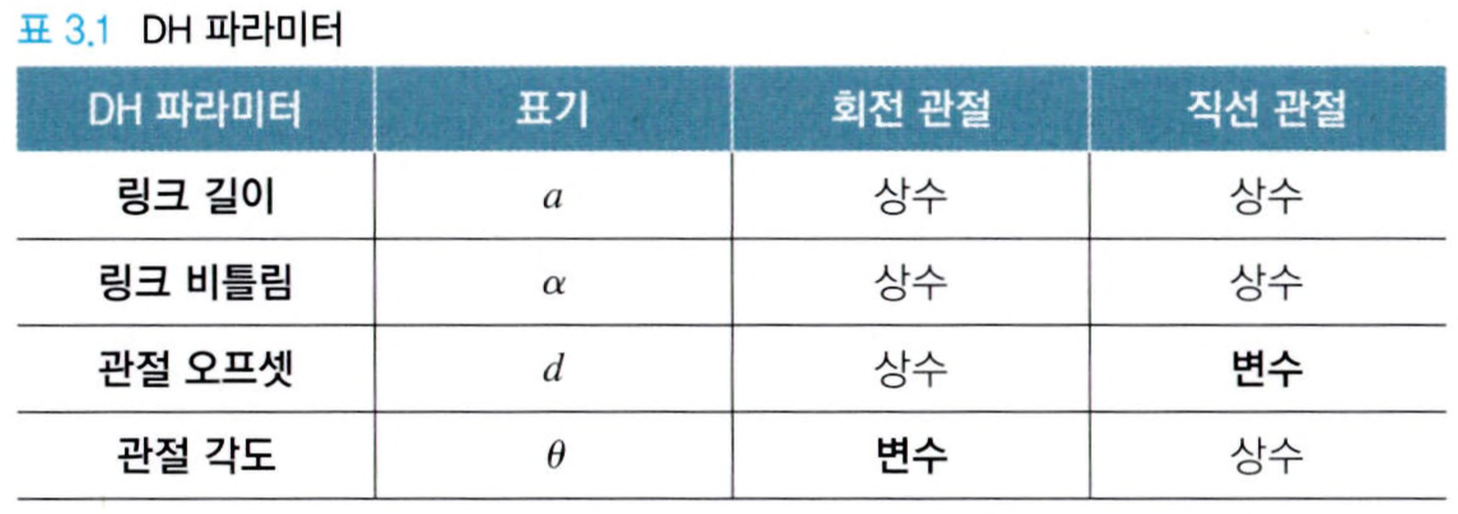
회전 관절의 경우 관절 각도를 제외한 모든 파라미터는 미리 정해지는 상수입니다. 반면에 직선 관절의 경우 관절 오프셋을 제외한 나머지 파라미터가 상수가 되는데요, 직선 관절의 경우 관절 오프셋이 변수이기 때문에 관절 거리라고 말하는 것이 좀 더 자연스러운 표현입니다.

위 4개의 파라미터를 통해 동차 변환 행렬을 상대 변환 방식으로 구할 수 있습니다.

\[T^{i-1}_i = R_z(\theta_i)\cdot T_z(d_i)\cdot T_x(a_i)\cdot R_x(\alpha_i)\] \[T^{i-1}_i =\begin{bmatrix} cos\theta_i & -sin\theta_icos\alpha_i & sin\theta_isin\alpha_i & a_icos\theta_i \\ sin\theta_i & cos\theta_icos\alpha_i & -cos\theta_isin\alpha_i & a_isin\theta_i \\ 0 & sin\alpha_i & cos\alpha_i & d_i \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

동차 변환 행렬의 구성이 다소 복잡해 보이긴 하지만, 실제로는 4개의 파라미터 중 몇개는 0이기 때문에 식이 많이 간소화됩니다.

정기구학

정기구학이란 관절 변수가 주어졌을 때 변환 행렬을 이용해 말단부의 자세를 구하는 문제를 의미합니다. 다른 이름으로는 직접 기구학(Direct Kinematics)라고도 불립니다.

SCARA 로봇의 정기구학

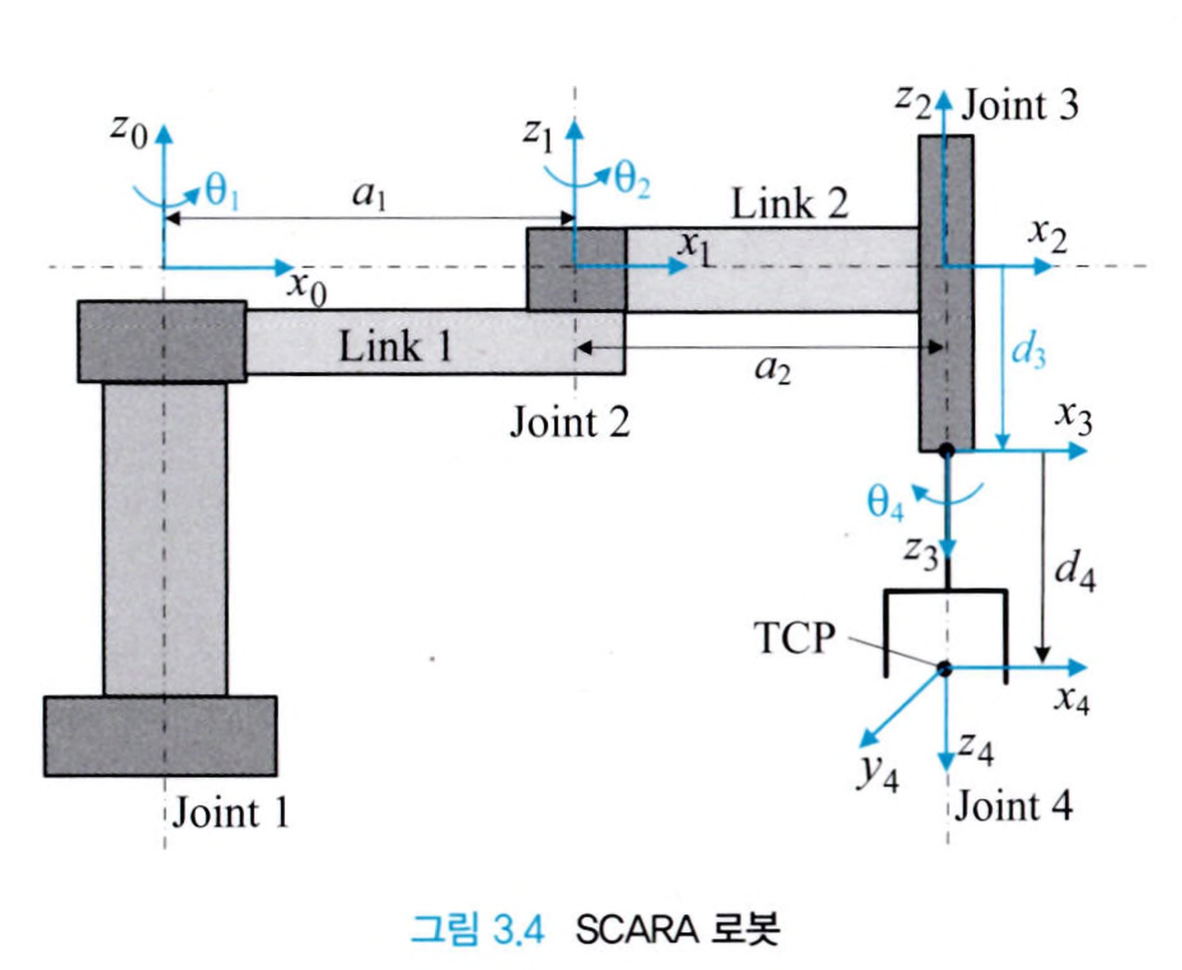
image-20241027163157403

SCARA 로봇의 대략적인 형태는 평면 2링크 로봇팔과 거의 유사합니다. 위 로봇에서 관절 변수는 $(\theta_1, \theta_2, d_3, \theta_4)$입니다.

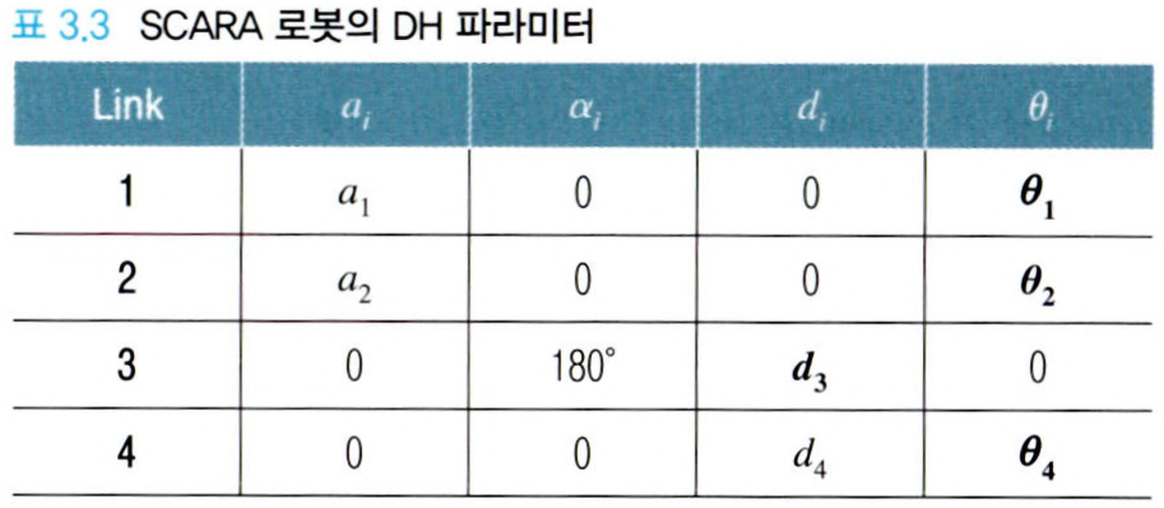
image-20241027165739163

SCARA 로봇의 DH 파라미터는 위와 같습니다. DH 파라미터를 알면 동차 변환 행렬을 구할 수 있고, 상대 변환의 방식으로 동차 변환 행렬들을 합성하여 말단의 자세와 위치를 구할 수 있습니다.

\[T^0_1T^1_2T^2_3T^3_4 = \begin{bmatrix} cos(\theta_1 + \theta_2 - \theta_4) & sin(\theta_1 + \theta_2 - \theta_4) & 0 & a_1cos(\theta_1) + a_2cos(\theta_1 + \theta_2) \\ sin(\theta_1 + \theta_2 - \theta_4) & -cos(\theta_1 + \theta_2 - \theta_4) & 0 & a_1sin(\theta_1) + a_2sin(\theta_1 + \theta_2) \\ 0 & 0 & -1 & d_3 - d_4 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

위 동차 변환 행렬을 통해 기저부에서 말단부로 바로 이동할 수 있습니다. 앞서 다룬 내용으로, 동차 변환 행렬에서는 위치를 움직이는 부분과 방위를 움직이는 부분이 분리돼 있습니다. 따라서 위 행렬에서 정기구학의 해를 바로 얻을 수 있습니다.

PUMA 로봇의 정기구학

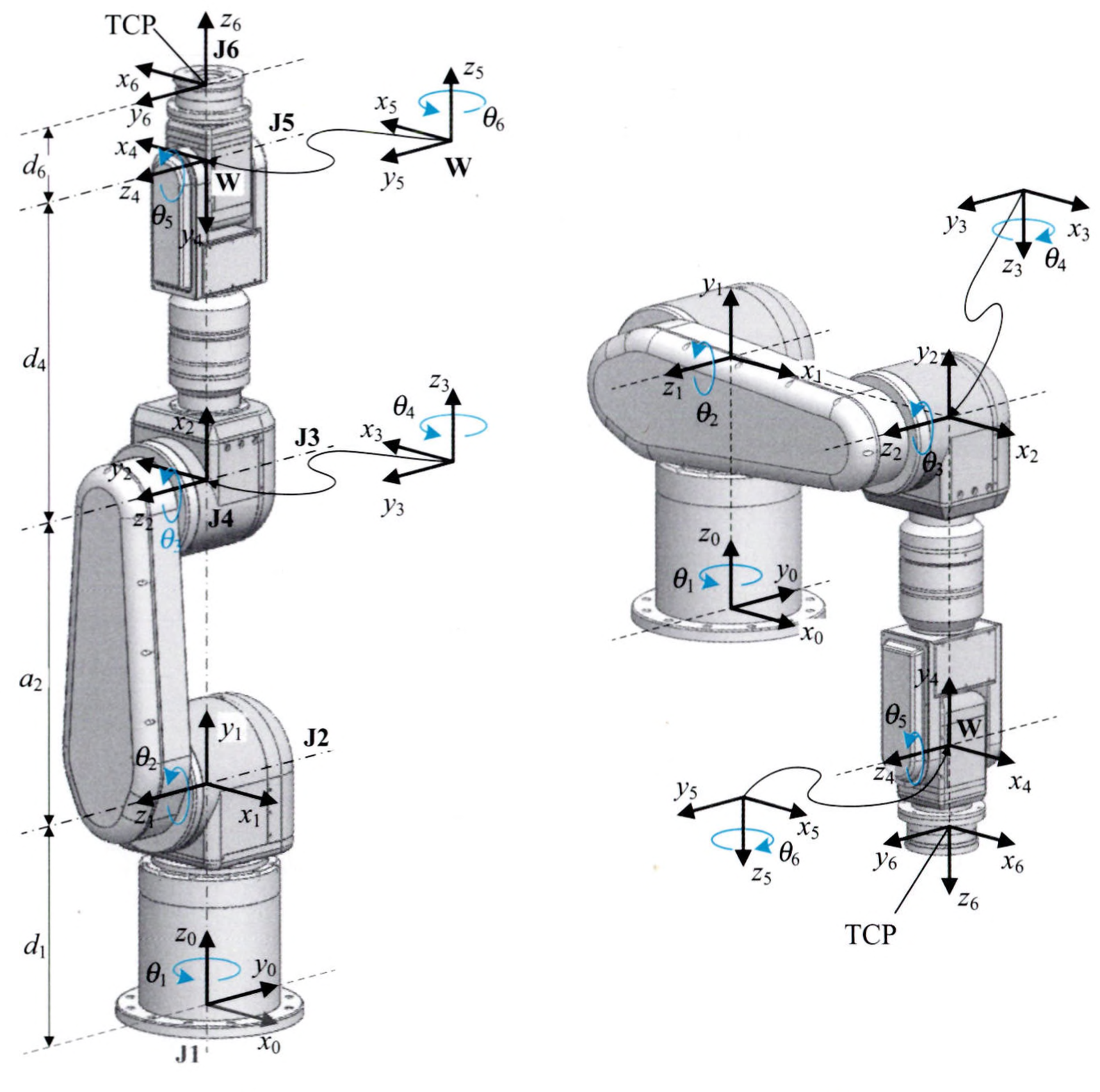
image-20241027171259252

PUMA 로봇은 3자유도의 공간 팔과 구형 손목으로 구성되어 있습니다. 몸체부인 공간팔은 손목점의 위치를 결정하고, 손목부는 말단부의 방위를 결정하는데요, 이와 같이 6자유도의 로봇 팔을 몸체부와 손목부로 분리하는 것을 기구학적 분리(Kinematic Decoupling)이라고 합니다.

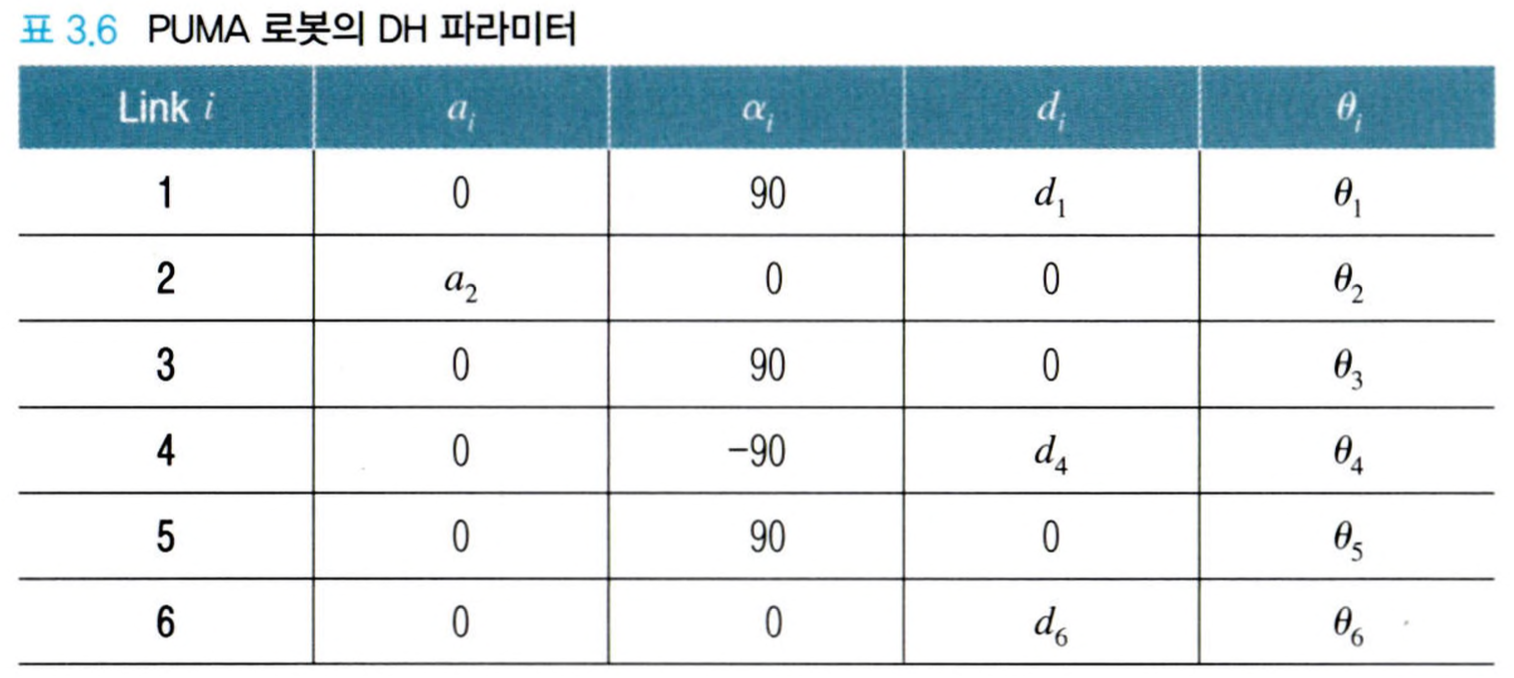
image-20241027171351032

PUMA 로봇의 DH 파라미터는 위와 같습니다. 위 파라미터를 이용해 동차 변환 행렬을 계산하여 아래와 같습니다.

\[T^0_1 = \begin{bmatrix} cos\theta_1 & 0 & sin\theta_1 & 0 \\ sin\theta_1 & 0 & -cos\theta_1 & 0 \\ 0 & 1 & 0 & d_1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\] \[T^1_2 = \begin{bmatrix} cos\theta_2 & -sin\theta_2 & 0 & a_2cos\theta_2 \\ sin\theta_2 & cos\theta_2 & 0 & a_2sin\theta_2 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\] \[T^2_3 = \begin{bmatrix} cos\theta_3 & 0 & sin\theta_3 & 0 \\ sin\theta_3 & 0 & -cos\theta_3 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\] \[T^3_4 = \begin{bmatrix} cos\theta_4 & 0 & -sin\theta_4 & 0 \\ sin\theta_4 & 0 & cos\theta_4 & 0 \\ 0 & -1 & 0 & d_4 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\] \[T^4_5 = \begin{bmatrix} cos\theta_5 & 0 & sin\theta_5 & 0 \\ sin\theta_5 & 0 & -cos\theta_5 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\] \[T^5_6 = \begin{bmatrix} cos\theta_6 & -sin\theta_6 & 0 & 0 \\ sin\theta_6 & cos\theta_6 & 0 & 0 \\ 0 & 0 & 1 & d_6 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\]

위 행렬들을 모두 차례대로 곱하면 $T^0_6$을 구할 수 있는데, 해당 행렬에서 위치 기구학과 방위 기구학을 구할 수 있습니다.

댓글남기기

참고