로보틱스 02: 벡터와 좌표의 변환

글에 들어가기 앞서…

이 포스팅은 ‘로보틱스‘에 대한 내용을 담고 있습니다.

자료 출처: 정슬, 로봇공학, 5판, / 송재복, 로봇 팔의 설계 및 제어 / F. C. Park and K. M. Lynch, Introduction to Robotics

벡터와 좌표의 변환

공학을 배운 지 그리 긴 시간이 흐르진 않았지만, 세상 거의 모든 것들이 벡터, 행렬로 표현되는 것 같습니다. 로봇도 예외가 아니라고 합니다. 로봇의 위치, 운동을 어떻게 벡터, 행렬로 표현하는지 알아보겠습니다.

로봇의 좌표

로봇의 좌표가 어떻게 표현되는지, 좌표가 표현되는 공간을 어떻게 부르는지 살펴봅니다.

• https://rbtx.com/en-US/components/robots/epson-prosix-vt6-a901s-reach-920mm-6kg-payload?lang=ko-KR

일반적으로 ‘로봇 팔‘이라고 하면 위와 같이 봉과 관절로 이루어진 모습을 떠올리는데요, 로봇 팔이 고정되어 있는 위치가 있고, 가장 끝에는 임무를 수행할 수 있는 도구가 달려있는 형태입니다. 로봇 팔의 기준이 되는 좌표를 World Coordinate, Fixed Coordinate, Global Frame, Reference Frame이라고 부르고, 로봇 팔의 끝에 달려있는 end-effector, 툴의 좌표를 Local Coordinate, Relative Frame, Moving Frame이라고 부릅니다. 그리고 이 툴의 좌표는 Cartesian Space에서 표현되는데요, 우리는 이 로봇 툴의 공간인 Cartesian Space에서 작업을 수행하기 때문에, 각 관절의 움직임, 거리가 Cartesian Space에 어떻게 작용하는지 이해하는 것이 중요합니다.

좌표의 표현

기본적인 좌표의 설정은 오른손 법칙을 따릅니다. $Z$축을 엄지손가락에 두고 감싸는 방향대로 $X$축과 $Y$축을 결정합니다.각 축 방향의 크기가 1인 단위벡터를 $X$, $Y$, $Z$ 순서대로, $i$, $j$, $k$라고 명명합니다.

좌표계 간의 관계

같은 물체는 어떤 좌표계에 표현되느냐에 따라 다르게 표현됩니다. 만약 우리가 두 좌표계의 단위벡터를 안다면, 이 두 좌표계 사이의 관계식을 작성할 수 있고, 이 관계식을 통해 한 좌표계에서 표현된 점이 다른 좌표계에서 어떻게 표현되는지 바로 구할 수 있습니다.

두 좌표계를 정의하고, 좌표계 사이의 관계식을 표현하겠습니다.

• 기본 전역 좌표($OXYZ$)

• 국부 좌표($OUVW$)

기본 전역 좌표의 단위벡터는 $i_x$, $j_y$, $k_z$이고, 국부 좌표의 단위벡터는 $i_u$, $j_v$, $k_w$라고 하겠습니다. 두 좌표계 사이의 스케일의 차이가 없다면, 병진운동과 회전운동을 통해 두 좌표계의 관계를 완전하게 표현할 수 있습니다.

두 좌표의 원점이 동일한 경우

두 좌표계의 원점이 동일하다면 오직 회전운동을 통해 두 좌표계 사이의 관계를 표현할 수 있습니다.

\[P_{xyz} = [P_x\space P_y \space P_z]^T = P_xi_x + P_yi_y + P_zi_z\] \[P_{uvw} = [P_u\space P_v \space P_w]^T = P_ui_u + P_vi_v + P_wi_w\]

국부 좌표가 주어져 있다면, 우리가 알지 못하는 것은 기본 전역 공간의 각 단위벡터의 크기성분인, $P_x$, $P_y$, $P_z$입니다. 그리고 이 값은 내적을 통해 쉽게 구해집니다.

\[P_x = i_x \cdot P = i_x \cdot P_{uvw} = i_x \cdot (P_ui_u + P_vi_v + P_wi_w)\] \[P_y = i_y \cdot P = i_y \cdot P_{uvw} = i_y \cdot (P_ui_u + P_vi_v + P_wi_w)\] \[P_z = i_z \cdot P = i_z \cdot P_{uvw} = i_z \cdot (P_ui_u + P_vi_v + P_wi_w)\]

위의 연산을 통하면 두 좌표계 사이의 변환이 이루어집니다. 이를 행렬 연산으로 간단하게 정리하면 아래와 같습니다.

\[\begin{bmatrix} P_x \\ P_y \\ P_z \end{bmatrix} = \begin{bmatrix} i_x \cdot i_u & i_x \cdot i_v & i_x \cdot i_w \\ i_y \cdot i_u & i_y \cdot i_v & i_y \cdot i_w \\ i_z \cdot i_u & i_z \cdot i_v & i_z \cdot i_w \end{bmatrix} \begin{bmatrix} P_u \\ P_v \\ P_w \end{bmatrix}\]

위 식에서 우변의 첫 번째 행렬을 회전행렬(Rotation Matrix)라고 명명하고 $R$으로 나타냅니다.

\[P_{xyz} = R\cdot P_{uvw}\]

회전행렬을 orthnormal합니다. 따라서 역행렬 대신 전치행렬을 사용할 수 있습니다.

회전행렬 R은 각 축별로 회전한 각도에 따라 이를 구하는 공식이 알려져 있는데요, 사실 이는 직접 내적을 해보면 왜 그러한지 바로 확인할 수 있습니다.

1. $X$축을 중심으로 $\psi$만큼 회전

   \[R_{X, \psi} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \psi & -\sin \psi \\ 0 & \sin \psi & \cos \psi \end{bmatrix}\]

2. $Y$축을 중심으로 $\psi$만큼 회전

\[R_{Y, \psi} = \begin{bmatrix} \cos \psi & 0 & \sin \psi \\ 0 & 1 & 0 \\ -\sin \psi & 0 & \cos \psi \end{bmatrix}\]

1. $Z$축을 중심으로 $\psi$만큼 회전

\[R_{Z, \psi} = \begin{bmatrix} \cos \psi & -\sin \psi & 0 \\ \sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

• 회전의 방향은 항상 오른손 법칙을 따른다는 점을 주의해야 합니다!

  회전행렬의 합성은 회전행렬의 행렬곱을 통해 이루어지는데요, 먼저 적용되는 회전행렬이 오른쪽에 위치하도록 곱해줍니다. 당연하게도 교환법칙이 성립되지 않기 때문에 항상 회전행렬을 곱하는 순서에 유의해야 합니다.

  이 회전행렬은 로봇 팔 끝의 end-effector의 오리엔테이션을 표현할 때 사용됩니다. 오리엔테이션을 표현할 수 있는 방법은 무수히 많지만, 최대 3번의 회전을 통해 모든 오리엔테이션을 표현할 수 있고, 이를 오일러 각이라고 합니다. 오리엔테이션을 결정할 때, 기본 전역 좌표를 기준으로 회전을 할 수도, 국부 좌표를 기준으로 회전을 할 수도 있습니다. 단, 이 때에 회전행렬을 만드는 식에 차이가 있습니다.

1. 기본 전역 좌표를 기준으로 회전을 하는 경우

   기본 전역 좌표를 기준으로 회전을 할 때, 먼저 적용되는 회전을 나타내는 회전 행렬이 오른쪽에 위치합니다. 예를 들어, $X$축을 기준으로 $\psi$만큼 회전하고, $Y$축을 기준으로 $\theta$만큼 회전한다면, 회전행렬을 구하는 식은 아래와 같습니다.

\[R = R_{y,\theta}\cdot R_{x,\psi}\]

1. 국부 좌표를 기준으로 회전을 하는 경우

   국부 좌표를 기준으로 회전을 할 때, 기본 전역 좌표와 달리 먼저 적용되는 회전을 나타내는 회전 행렬이 왼쪽에 위치합니다. 즉, 회전행렬의 행렬 곱이 회전의 순서와 동일하게 순차적으로 이루어집니다. 좌표계 자체가 회전을 하는 것인데, 어떻게 단순히 행렬 곱의 순서를 반대로 하는 것만으로 충분히 표현되는 걸까요?

   예를 들어, $X$축을 기준으로 $\psi$만큼 회전하고, $V$축을 기준으로 $\theta$만큼 회전한다면, 회전행렬을 구하는 식은 아래와 같습니다.

   \[R = R_{x,\psi}\cdot R_{y,\theta}\] \[R = R_{x,\psi} \cdot R_{v,\theta} = R_{x,\psi} \cdot R_{y,\theta}\]

   괄호를 추가해 좀 더 알기 쉽게 나타내면 아래와 같습니다.

   \[P_{xyz} = R_{x,\psi} \cdot (R_{y,\theta} \cdot P_{uvw})\]

   회전이 기본 전역 좌표의 고정된 축을 중심으로 회전하는 것이 아닌, 계속해서 회전하는 국부 좌표의 축을 기준으로 회전을 하기 때문에, 회전된 좌표계에서 한 번씩만 회전이 적용됩니다. 이러한 이유로 먼저 적용되는 회전이 회전 행렬의 왼쪽에 위치하게 됩니다.

atan2

회전할 각도를 알면 회전행렬을 구할 수 있는데, 그 반대 방향도 당연히 가능합니다. 그리고 이 해를 구하기 위해서, atan2함수가 필요합니다. atan2는 $arctan$함수의 변형 함수입니다. $arctan$함수에 들어가는 값은 단일 실수 삾으로 들어가고, 그 치역은 $-\pi/2$ 부터 $+\pi/2$까지 입니다. 하지만, 이 함수로는 모든 각도를 다루기 어렵습니다.

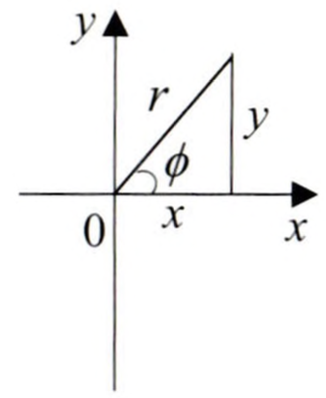
$arctan$함수는 (1, 1)과 (-1, -1)를 동일한 값으로 반환합니다. 애초에 $arctan$함수는 정의역으로 $x/y$를 받기 때문에 위의 입력의 차이를 구분조차 할 수 없죠. 하지만 우리가 실제로 다루는 세계에서는 이러한 차이점을 구분할 필요가 있고, 이를 위해 atan2라는 새로운 함수를 사용합니다.

위와 같이 정의된 atan2함수를 사용하면 전체 각도를 다르게 표현할 수 있습니다. 로봇 기구학에서 사용되는 모든 각도는 반드시 이 atan2함수를 사용해 나타냅니다.

\[\phi = atan2(k\cdot y, k\cdot x) = atan2(y, x)\space for \space k > 0\] \[\phi = atan2(y, x) = atan2(sin\phi, cos\phi)\]

atan2함수의 입력 값을 동일한 값으로 나누어 주어도 그 결과 값은 동일한데요, 다만, 나눠주는 수는 반드시 양수여야 합니다. atan2는 양수와 음수를 다른 각도로 반환하기 때문에 음수로 나눠주게 값이 유지되지 않습니다.

이 atan2 함수를 이용하면 회전행렬의 9개의 값이 구해질 때, 각 축으로 얼만큼 회전해야하는지를 역으로 구할 수 있습니다. 주의할 점은 구해지는 각도의 종류가 2개 이상이라는 점입니다. 회전 행렬은 회전한 이후 방향성을 가리키는 행렬이라고 생각할 수 있는데요, 해당 방향으로 회전하는 방법은 유일하게 존재하지 않기 때문에 식을 풀어 해를 구해봐도 2개 이상의 해를 항상 얻게 됩니다.

롤, 피치, 요의 표현

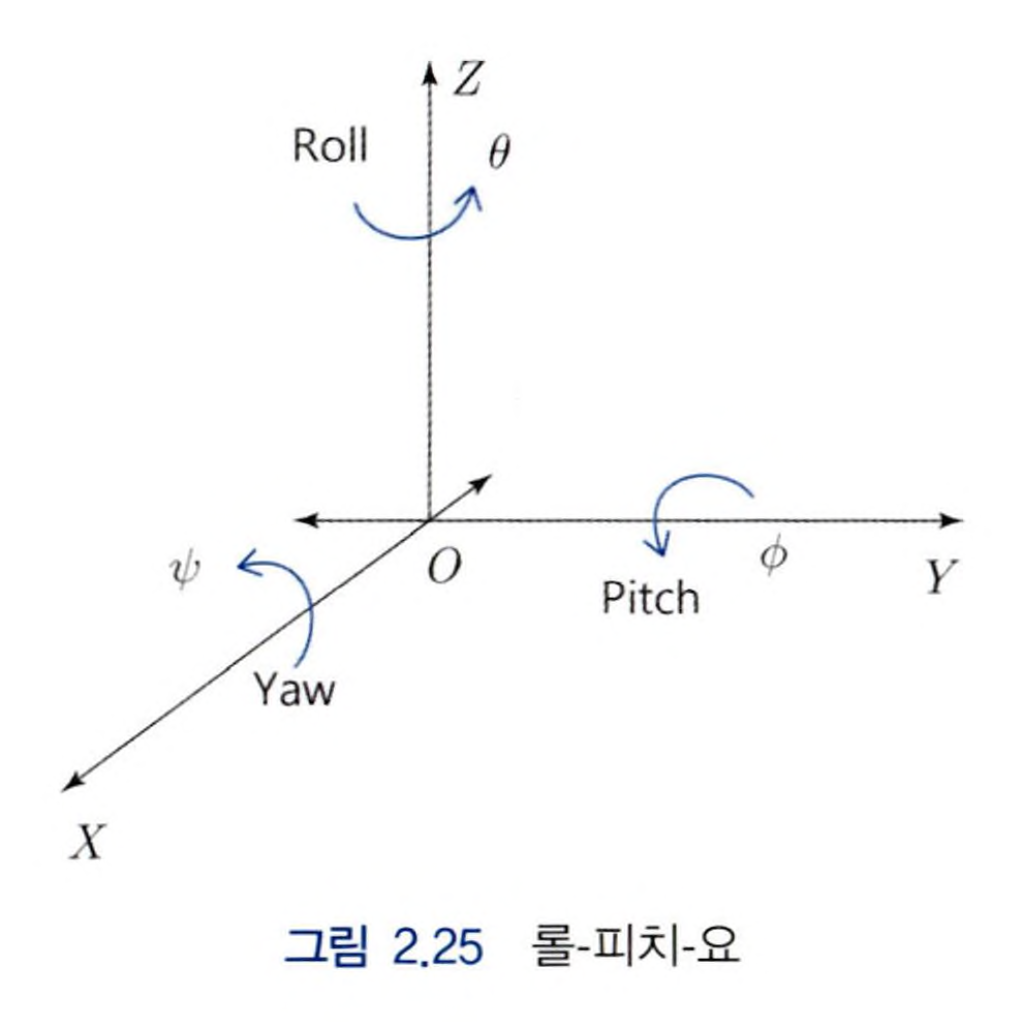
기계공학이 아닌 다양한 분야에서 롤, 피치, 그리고 요라는 표현이 종종 사용되는데요, 위 그림과 같은 축 중심의 회전을 의미합니다. 정확하게 표현하면, $X$축 방향 회전을 요(yaw), $Y$ 방향 회전을 피치(pitch), $Z$ 방향 회전을 롤(roll)이라고 합니다. 이러한 용어는 항공기의 조종에서도 사용되는데요, 비행기의 경우, 롤은 비행기의 날개가 수평을 벗어나는 정도, 피치는 비행기의 앞뒤 기울기, 요는 비행기의 좌우 기울기를 의미합니다.

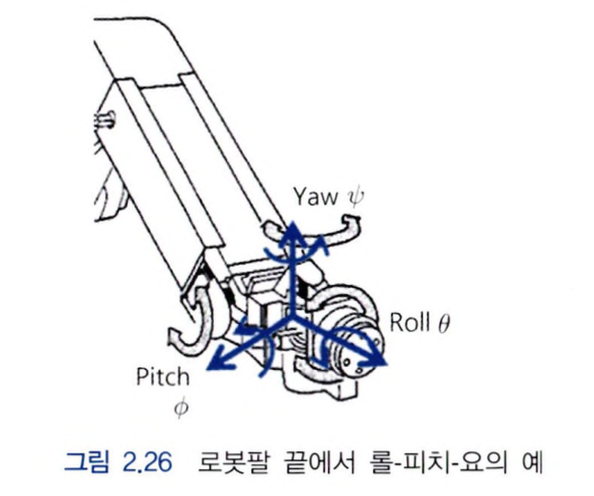
Robotics에서는 이를 비행기 대신 로봇을 대상으로 회전을 설명하는데 사용합니다. 그림으로 보면 위와 같습니다.

로봇 팔 끝에서의 회전행렬

\[R = \begin{bmatrix} n_x & s_x & a_x \\ n_y & s_y & a_y \\ n_z & s_z & a_z \\ \end{bmatrix} = \begin{bmatrix}\bar{n} & \bar{s} & \bar{a}\end{bmatrix}\]

로봇 팔 끝에 있어서 회전행렬을 오리엔테이션을 나타냅니다. 회전행렬의 각 열이 로봇 팔 끝이 향하고 있는 오리엔테이션의 각 축을 의미하게 됩니다.

• $\bar{n}$: normal 벡터 = $XYZ$좌표에 $U$축의 프로젝션을 나타냄
• $\bar{s}$: normal 벡터 = $XYZ$좌표에 $V$축의 프로젝션을 나타냄
• $\bar{a}$: normal 벡터 = $XYZ$좌표에 $W$축의 프로젝션을 나타냄

그리고 회전행렬은 orthnormal하기 때문에 특별한 성질을 가집니다.

• 회전행렬의 열백터는 기본 전역 좌표에 대한 국부 좌표를 나타냄
• 회전행렬의 행벡터는 국부 좌표에 대한 기본 전역 좌표를 나타냄

위의 성질들이 구체적으로 어떤 의미인지 아래 예시를 통해 살펴봅니다.

예제 2.13

\[R = \begin{bmatrix} 0 & 0& -1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{bmatrix}\]

위 회전행렬의 열벡터들은 아래와 같습니다.

• $\begin{bmatrix} 0 & 0 & -1 \end{bmatrix} $
• $\begin{bmatrix} 0 & 1 & 0 \end{bmatrix} $
• $\begin{bmatrix} 1 & 0 & 0 \end{bmatrix} $

위 벡터들이 차례대로 기본 전역 좌표의 각 축에 대한 국부 좌표를 나타냅니다. 다시 말하면, 첫 번째 열벡터는 $\begin{bmatrix} 0 & 0 & -1 \end{bmatrix} $인데요, 이 열벡터는 기본 전역 좌표의 첫 번재 축인 $X$축에 대한 국부 좌표를 나타냅니다. 즉, $P_x = -P_w$이고 $W$축이 $X$축과 반대 방향으로 회전된 상태임을 알 수 있습니다.

축-각도 표현(axis-angle representation)

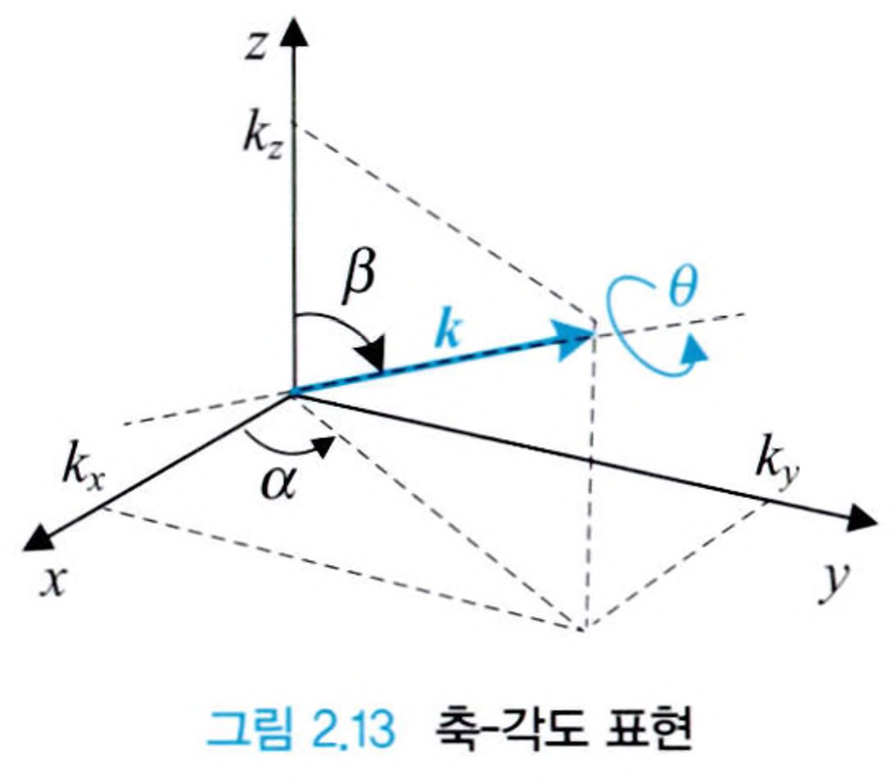
축-각도 표현은 공간상의 임의의 축에 대한 회전각으로 방위를 나타내는 방법입니다. 축을 표현하기 위해 3개($k_x$, $k_y$, $k_z$)의 파라미터가 필요하고, 이 축이 회전한 각을 나타내기 위해 1개의 파라미터($\theta$), 총 4개의 파라미터로 방위를 나타냅니다.

\[k = \begin{bmatrix} k_x^2 & k_y^2 & k_z^2 \end{bmatrix}^T\] \[k_x^2 + k_y^2 + k_z^2 = 1\]

총 4개의 파라미터를 사용하지만, 길이가 1로 표현돼야한다는 제약조건이 있기 때문에 3개의 파라미터만이 독립적이게 됩니다. 회전축 $k$에 대한 각도 $\theta$만큼의 회전을 나타내는 회전 행렬을 $R_k(\theta)$라고 하고 아래의 식을 통해 구할 수 있습니다.

\[R_k(\theta) = R_z(\alpha)R_y(\beta)R_z(\theta)R_y(-\beta)R_z(-\alpha)\]

식을 해석해 보면 기본 전역 좌표계에 $z$축을 일단 먼저 일치시키고 일치된 축에 대해서 $\theta$만큼 회전하는 회전 행렬임을 알 수 있습니다. 위 표현은 고정 좌표계에 대한 절대 변환에 해당합니다.

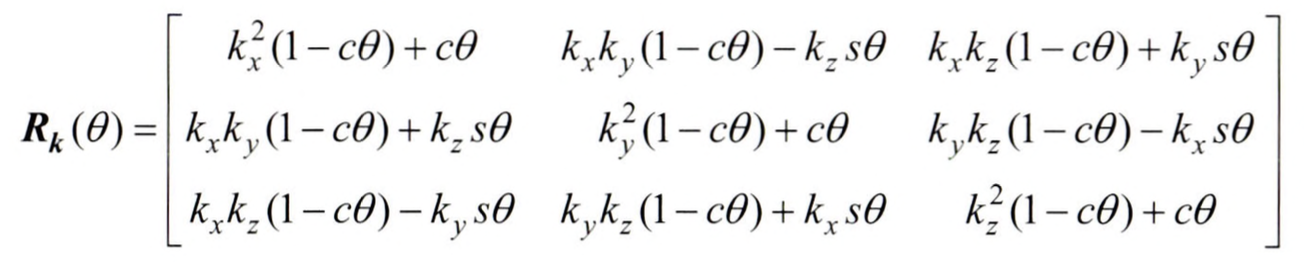
$k$축의 방위를 나타내는 좌표를 알고 있으므로, 삼각함수를 통해 회전행렬을 구하면 위와 같습니다. 위 행렬에서 대각 성분을 모두 더하면 $1 + 2cos\theta$가 되기 때문에 대각 성분을 통해 회전 각을 구할 수 있습니다.

\[\theta = cos^{-1}(\frac{r_{11} + r_{22} + r_{33} - 1} 2\ )\]

결론적으로는 아래와 같이 $k$를 구할 수 있겠습니다.

\[k = \frac{1}{2sin\theta}\begin{bmatrix} r_{32} - r_{23} \\ r_{13} - r_{31} \\ r_{21} - r_{12} \\ \end{bmatrix} for \space sin\theta \neq 0\]

위의 축-각도 표현에는 치명적인 문제점이 존재하는데, $\theta$의 값이 0 또는 $\pi$가 될 때 회전축이 정의되지 않는 특이점이 발생한다는 점입니다. 만약 축에 따라 회전을 하지 않았다면, 어떤 방향을 축으로 잡아도 동일합니다. 그리고 회전을 정확히 반 바퀴를 했다면, 기존에 의도했던 축과 정 반대 방향의 축 또한 만족됩니다.

또 하나의 문제점은, 항상 두 개의 해가 존재한다는 사실입니다. 예를 들어서 $k$축에 대해서 $\theta$만큼 회전하는 것이 우리가 의도했던 회전이라면, $-k$축에 대해서 $-\theta$만큼 회전하는 해도 동시에 구해집니다. 이것은 특이점과는 다른 종류의 문제인데, 위에서 언급한 반 바퀴를 돌렸을 때 두 가지 축이 존재하는 상황은 $k$축에 대해서 $\theta$만큼 회전한 해와 $-k$축에 대해서 $\theta$만큼 회전한 해, 두 가지가 존재하는 경우로 명백히 다른 경우입니다. 이 문제는 $q$의 범위를 제한하면 되므로 큰 문제는 아닙니다.

유닛 쿼터니언 표현(Unit Quaternion Representation)

유닛 쿼터니언 표현은 기본적으로 축-각도 표현과 동일한데, 특이점이 발생하지 않도록 표현 방식을 변경합니다.

\[\eta = cos\frac{\theta}2\] \[\epsilon = \begin{bmatrix} \epsilon_x & \epsilon_y & \epsilon_z \end{bmatrix}^T =sin\frac{\theta}2 \cdot k =sin\frac{\theta}2 \cdot \begin{bmatrix} k_x & k_y & k_z \end{bmatrix}\]

위의 두 식을 사용하면 아래와 같은 구속 조건을 구할 수 있습니다.

\[\eta^2 + \epsilon_x^2 + \epsilon_y^2 + \epsilon_z^2 = 1\]

유닛 쿼터니언 역시 4개의 파라미터를 사용하지만 1개의 구속 조건이 있기 때문에 3개의 파라미터만이 독립적입니다.

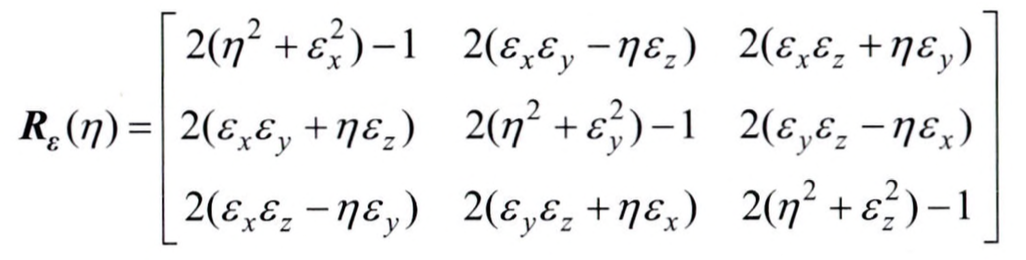
회전 행렬을 구하면 위와 같은데, 역시 반대로 회전행렬이 주어져 있을 때, 회전 축과 회전 각도를 구할 수 있습니다.

\[\eta = \frac{1}2 \sqrt{r_{11} + r_{22} + r_{33} + 1}\] \[\epsilon = \frac{1}2 \begin{bmatrix} sgn(r_{32} - r_{23}) \sqrt{r_{11} - r_{22} - r_{33} + 1}) \\ sgn(r_{13} - r_{31}) \sqrt{r_{22} - r_{33} - r_{11} + 1}) \\ sgn(r_{21} - r_{12}) \sqrt{r_{33} - r_{11} - r_{22} + 1}) \\ \end{bmatrix}\]

축-각도 표현에 비해 직관적이지 않은 표현임은 분명하지만, 축-각도 표현이 가지는 치명적인 단점인 특이점이 존재하지 않기 때문에 축-각도 표현으로 표현할 때에는 반드시 유닛 쿼터니언 표현을 사용합니다.

두 좌표의 원점이 서로 떨어져 있을 경우

이전 내용들은 회전 좌표의 원점과 기본 전역 좌표의 원점이 동일한 경우들입니다. 사실 회전행렬은 회전만을 다룰 수 있기 때문에 원점이 다를 수가 없습니다. 그러나 실제 로봇 팔에서는 end-effector가 기본 전역 좌표의 원점에서 벗어나 다양한 곳을 이동하면서 기능을 수행하는데요, 아래에서는 이를 표현하는 방식에 대해서 살펴봅니다.

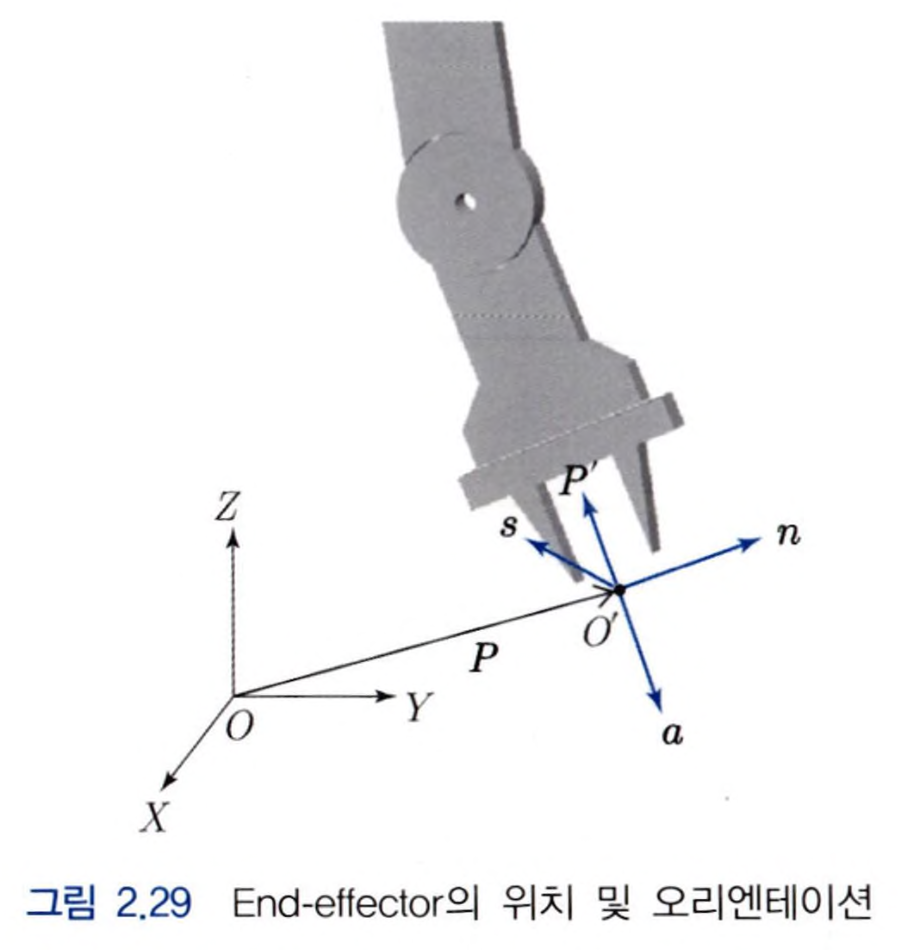
로봇 팔이 원점을 벗어나 움직여도 특별히 크게 달라지는 점은 없습니다. 단지 로봇의 이동을 의미하는 병진운동이 추가될 뿐인데요, 이러한 병진운동과 기존의 회전운동을 나타내는 행렬을 합쳐서 하나의 행렬로 표현할 수 있습니다. 이를 Homogeneous Translation 행렬 이라고 표현합니다.

\[T = \begin{bmatrix} R^{3\times3} & P^{3\times1} \\ f^{1\times3} & 1 \end{bmatrix}\]

위 식에서 $P^{3\times1}$이 기본 좌표에 대해 회전한 좌표의 위치 벡터, 그러니까 병진 운동을 의미하고, $f^{1\times3}$는 컴퓨터 비전 혹은 캘리브레이션을 위한 벡터입니다(거의 대부분의 경우에 0).

\[P_{xyz} = TP_{vuw}\]

로봇 팔은 여러 개의 조인트로 이루어져 있는데, 각각의 링크 사이의 관계를 나타내는 Translation 행렬을 모두 곱하면, 결과적으로 기본 전역 좌표와 국부 좌표 사이의 관계를 알 수 있을 것입니다.

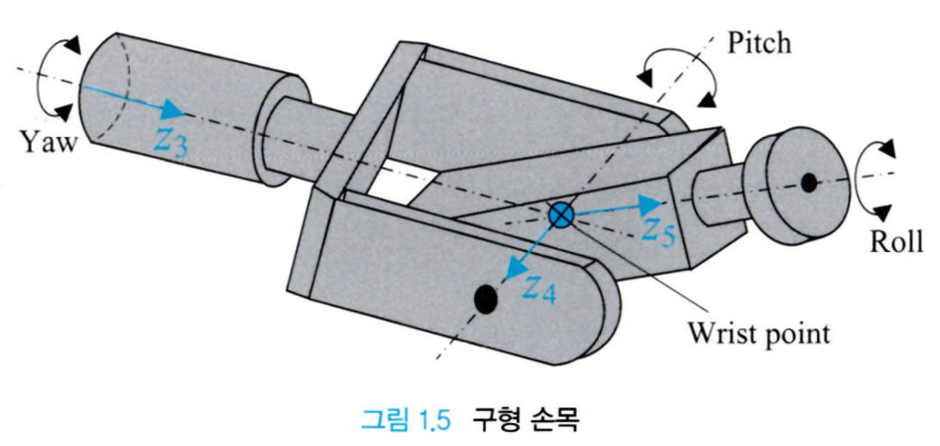
6축 로봇의 경우 처음 3조인트에 의해 병진운동이 정의되고 나중 3조인트를 통해 오리엔테이션이 결정됩니다.

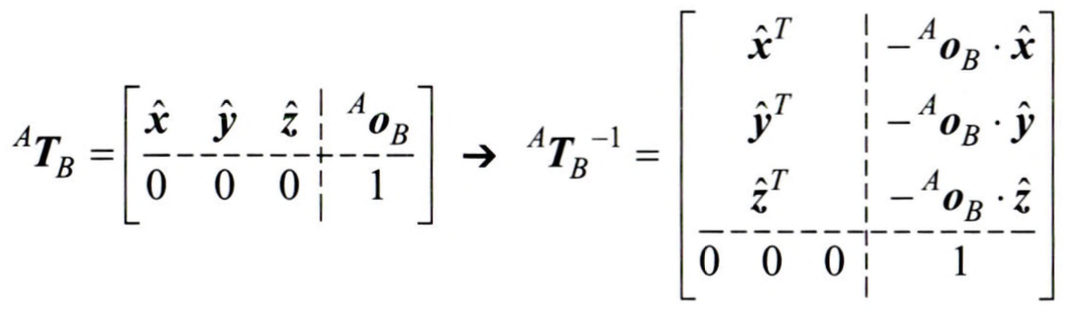
Homogenuous Translation 행렬은 Rotation 행렬과 달리 orthonormal하지 않습니다. 따라서, $T^T = T^{-1}$이 반드시 성립하진 않습니다.하지만, Translation 행렬의 구성 성분 중 Rotation 행렬이 Orthonormal하기 때문에 역행렬을 비교적 쉽게 구할 수 있습니다.