강화학습 알고리즘: TRPO(Trust Region Policy Optimization)

이 포스팅은 ‘강화학습 알고리즘‘에 대한 내용을 담고 있습니다.

자료 출처: 단단한 강화학습, Reinforcement Learning An Introduction , 2nd edition. 리처드 서튼, 앤드류 바트로, 김성우(옮긴이), https://www.youtube.com/watch?v=Ukloo2xtayQ

TRPO(Trust Region Policy Optimization)

DDPG는 굉장히 훌륭한 알고리즘이지만, 성능의 단조 향상이 보장되지 않는다는 큰 문제점이 있습니다. 성능이 단조 향상하지 않는다는 것은 우리가 파라미터를 최적화할 때, 목적함수의 증가가 일어나지 않을 수 있다는 것을 의미합니다. 이러한 불명확함은 알고리즘의 학습에 불안정성을 야기하고, 알고리즘이 Step Size에 굉장히 민감하게 반응하게 만듭니다.

TRPO(Trust Region Policy Optimization)은 DDPG의 상기 문제점을 신뢰 구역(Trust Region)이라는 아이디어를 도입해 해결합니다. 신뢰 구역은 KL(Kullback-Leibler)-divergence로 정의되는데, 이 구역 내에서 파라미터 업데이트가 일어날 때 성능의 단조 향상이 보장되고, Step Size의 영향으로부터 벗어나게 됩니다.

TRPO 논문에는 단조 향상이 이론적으로 완벽하게 보장되는 알고리즘을 소개하는데요, 이 알고리즘을 실제로 구현하는 것이 꽤나 어렵습니다..(거의 불가능합니다.) 때문에 이론적인 TRPO에서 출발해 여러 번 근사시켜 보다 실용적인 알고리즘을 유도합니다. 그럼에도 구현이 꽤나 복잡하고 방대한 계산량을 필요로 하기 때문에 정책망의 크기가 조금만 커져도(CNN, RNN의 수준을 감당할 수 없음) 학습시키기 곤란하다는 단점이 있습니다.

Trust Region

위의 사진을 통해 ‘Trust Region이 왜 필요한가?’에 대한 직관적인 이해를 얻을 수 있습니다. DDPG는 경사 상승을 통해 파라미터를 업데이트합니다. 지금 밟고있는 땅에서 올라가는 방향으로 걸음을 내딛는 일과 동일합니다. 여기에서 가장 큰 이슈는 ‘내가 여기서 얼마나 큰 발걸음을 할 수 있는가?’입니다. 알고리즘이 빠르게 수렴하기 위해서는 걸음을 크게 설정해야 하지만, 그랬다가는 낭떨어지로 빠질 위험이 굉장히 높아집니다. 그렇다고 걸음을 작게 설정하면 알고리즘이 수렴할 때까지 오랜 시간을 소요하게 됩니다.

신뢰 구역은 내가 얼마나 발을 내딛을 수 있는지, 그 범위를 의미합니다. 신뢰 구역이 에이전트에게 전해지면 에이전트는 해당 구역 내에서는 안전하다는게 보장되기 때문에 가장 높이 올라가는 방향으로 큰 발걸음을 내딛을 수 있게 됩니다. 때문에 Step Size로부터 자유로워지고, 성능의 단조 향상이 보장되기 때문에 국소 최적점일지 전역 최적점일지는 모르겠지만 아무튼 최적점에 도달하게 됩니다.

TRPO 알고리즘의 핵심 아이디어

\[\eta(\pi) = E_{s_0, a_0, ...}[\sum_{t=0}^{\infty}\gamma^tr(s_t)]\]

TRPO 알고리즘의 손실함수는 기대 이득으로 설정됐습니다. 특정 에피소드의 모든 상태에서 받은 보상의 감쇠합으로 정의됩니다.

\[\eta(\pi)\] \[= \eta(\pi_{old}) + E_{\tau \sim \pi}[\sum_{t=0}^\infty \gamma^tA_{\pi_{old}}(s_t, a_t)]\] \[= \eta(\pi_{old}) + \sum_s\rho_{\pi}(s)\sum_a\pi(a|s) A_{\pi_{old}}(s, a)\]

새로운 정책의 목적 함수 값은 이전 정책의 목적 함수 값과 정책으로 정의할 수 있습니다(자세한 유도는 논문 참조). 위 식에서 단조 증가가 보장되기 위해서는 아래의 식이 항상 0보다 커야 합니다.

\[\sum_a\pi(a|s) A_{\pi_{old}}(s, a)\]

그런데 새로운 정책의 상태 방문 빈도($\rho_{\pi}(s)$)를 알아내는 것은 굉장히 많은 샘플링을 필요로 합니다. 때문에 전체 수식을 조금 다른 알고리즘으로 근사하게 되는데, 그렇게 하면 또 바로 위 식의 값이 음수가 될 가능성이 발생하게 됩니다. 이런 문제들을 해결하기 위해 신뢰 구역을 설정하게 되는건데요, 아래에서 자세하게 살펴보겠습니다.

Conservative Policy Iteration Update

\[\eta(\pi)= \eta(\pi_{old}) + \sum_s\rho_{\pi}(s)\sum_a\pi(a|s) A_{\pi_{old}}(s, a)\] \[L_{\pi_{old}}(\pi)= \eta(\pi_{old}) + \sum_s\rho_{\pi_{old}}(s)\sum_a\pi(a|s) A_{\pi_{old}}(s, a)\]

위에서 새로운 정책의 상태 방문 빈도를 계산하기 어렵다고 했는데요, 새로운 정책의 상태 방문 빈도를 사용하지 않고 이전 정책의 상태 방문 빈도를 사용하는 방법이 있습니다. 이를 국소 근사(Local Approximate)라고 합니다. 그냥 이전 정책의 상태 방문 빈도로 갈아끼워도 괜찮은건가.. 싶은데, 생각보다 정말 괜찮은 근사 함수가 됩니다.

• 이전 정책(Old Policy): $\pi_{old}$
• 새로운 정책(New Policy): $\pi_{old}$
• $L$에서 찾은 가장 좋은 정책: $\pi’$

\[L_{\pi_{\theta_0}}(\pi_{\theta_0}) = \eta(\pi_{\theta_0})\] \[\nabla_\theta L_{\pi_{\theta_0}} (\pi_{\theta}) |_{\theta = \theta_0} = \nabla_\theta\eta(\pi_{\theta})|_{\theta = \theta_0}\]

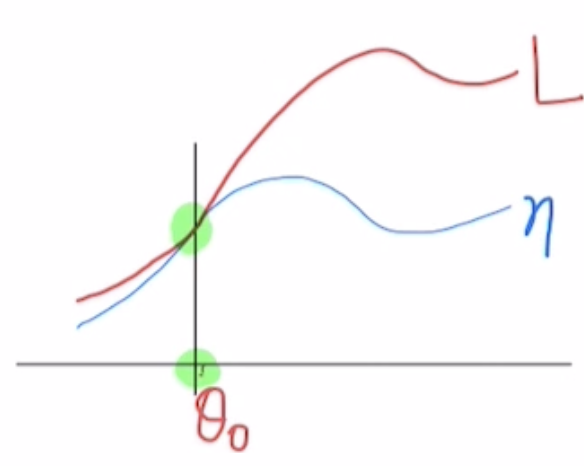
왜냐하면 일단 이전 정책과 동일한 정책일 때 같은 값을 가지고, 그 때의 기울기 값도 동일합니다. 정리하면 해당 지점의 위치와 그 위치에서 나아가는 방향성이 동일하다는 말인데, 때문에 작은 step에 대해서는 비슷한 변화를 가지므로 원래 손실함수의 향상을 가져올 수 있습니다. 하지만 어느정도의 step까지 괜찮은 건지는 아직 알 수 없습니다. 이런 문제를 다루기 위해서 Conservative Policy Iteration Update를 사용합니다.

\[\pi(a|s) = (1-\alpha)\pi_{old}(a|s) + \alpha\pi'(a|s)\] \[where \space \pi' = \arg \max_\pi L_{\pi_{old}}(\pi)\]

Conservative Policy Iteration Update에서는 기존 정책과 새로운 정책의 짬뽕 정책(Mixture Policy), 구체적으로는 EWMA를 사용한 지연 최적화 정책을 사용합니다. 이 때의 새로운 정책은 $L$상에서 가장 높았던 지점을 도달케하는 정책($\pi’$)을 의미합니다. **위의 짬뽕 정책을 사용할 때 우리가 얻을 수 있는 최고의 장점은 하한을 알 수 있다는 점입니다. 이 하한이 지속적으로 상승하도록 보장하는 최적화를 수행하면, 원래의 손실함수 또한 지속적으로 향상시킬 수 있을 것입니다.

\[\eta(\pi) \geq L_{\pi_{old}}(\pi) - \frac{2\epsilon \gamma}{(1-\gamma)^2} \alpha^2\] \[where \space \epsilon = \max_s[E_{a \sim \pi'(a|s)}[A_{\pi_{old}}(s, a)]]\]

위 식에서의 $\epsilon$은 $\pi’$ 정책에 따라서 행동을 할 때, 과거 정책($\pi_{old}$)의 어드밴티지 함수의 평균값을 각 상태별로 구할 수 있을 텐데, 상태별 평균값들 중 가장 큰 값을 $\epsilon$이 됩니다. 하지만 짬뽕 정책에서만 하한이 적용된다는 점 때문에 실제로는 사용이 굉장히 제한적입니다. 사실 $\epsilon$을 실제로 계산하는 것도 어렵지만, 짬뽕 정책 자체를 실제 코드로 적용하는 것도 어렵습니다.

General Stochastic Policy

하한을 알 수 있다는 큰 장점이 있음에도, EWMA 꼴로 엮여있는 짬뽕 정책에 대해서만 하한을 알 수 있기 때문에 이 하한을 활용할 수 있는 범위가 제한적이었습니다. 짬뽕 정책에 대해서 알려진 하한을 통해 그냥 어떤 새로운 정책에 대한 하한을 알 수 있도록 식을 변형합니다.

\[\alpha = \max_sD_{TV}(\pi_{old}(\cdot|s)||\pi(\cdot|s))\] \[\epsilon = \max_{s, a}|A_{\pi_{old}}(s, a)|\]

원래 식에서 $\alpha$는 EWMA의 가중 평균 정도를 결정하는 하이퍼파라미터였습니다. 여기서는 $\alpha$의 값을 Old Policy와 New Policy 분포 사이의 최대 총 분산 거리(Total Variation Distance, $D_{TV}$), 다시 말하면, 분포의 총 분산 거리가 최대가 되게 하는 $s$를 넣었을 때의 그 거리로 설정합니다. 그리고 $\epsilon$도 마찬가지로 위와 같이 모든 상태 행동 쌍에서의 최대 값으로 설정합니다.

\[D_{TV}(P, Q) = \frac{1}{2}||P - Q||_1\] \[D_{KL}(P||Q) = \int_xp(x)\log\frac{p(x)}{q(x)}dx\] \[D_{KL}^{max}(\pi_{old}, \pi) = \max_s D_{KL}(\pi_{old}(\cdot|s)||\pi(\cdot|s))\]

DTV와 DKL 사이에는 위와 같은 관계식이 성립합니다. 이 사실을 이용해 정리하면 아래와 같습니다.

\[\eta(\pi) \geq L_{\pi_{old}}(\pi) - CD^{max}_{KL}(\pi_{old}, \pi)\] \[where \space C = \frac{4\epsilon\gamma}{(1 - \gamma)^2}\]

이제 짬뽕 정책을 사용하지 않아도 하한을 알 수 있습니다.

MM(Minorization-Maximization) Algorithm

위 그림에서 MM 알고리즘의 동작을 한 눈에 확인할 수 있습니다. 위 그림에서 빨간색은 원래(Orginal) 목적 함수, 그리고 파란색이 대리(Surrogate) 목적 함수입니다. 예를 들어 현재 위치가 $\pi_i$일 때, 아래의 조건을 만족하는 대리 목적 함수를 설정합니다.

1. 대리 목적 함수는 현재 지점에서 원래 목적 함수와 접해야 합니다(값이 같고 기울기가 같음).
2. 대리 목적 함수는 항상 원래 목적 함수보다 작은 값을 가져야 합니다.
3. 대리 목적 함수는 원래 목적 함수보다 최적화하기 쉬운 함수를 사용합니다.

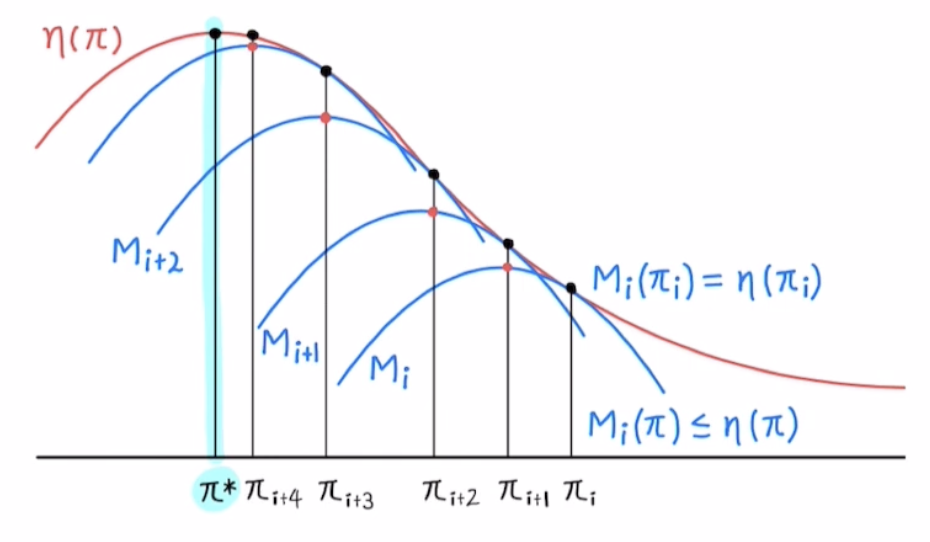
위의 조건들을 만족하는 대리 목적 함수를 구했다면, 최적화를 수행합니다.

1. 대리 목적 함수에서 최적 지점을 찾습니다.
2. 원래 목적 함수에서 위에서 찾은 최적 지점을 찾아갑니다.
3. 새롭게 찾은 최적 지점에서 다시 대리 목적 함수를 설정하고 동일한 작업을 반복합니다.

MM 알고리즘 적용

General Stochastic Policy에서 구한 하한은 MM 알고리즘의 대리 목적 함수의 조건에 완벽하게 부합합니다. 따라서 MM 알고리즘을 적용시키면 단조 성능 향상을 보장할 수 있습니다.

\[\eta(\theta) \geq L_{\theta_{old}}(\theta) - CD^{max}_{KL}(\theta_{old}, \theta)\] \[\max_{\theta}[L_{\theta_{old}}({\theta}) - CD_{KL}^{max}(\theta_{old}, \theta)]\]

위의 두 식을 비교를 해보겠습니다. 첫 번째 식에서 $\theta$를 찾으면, 그건 바로 최적 정책이 될 텐데요, 아래의 두 번째 식에서 구한 $\theta$는 그저 다음 정책에 불과합니다. 이 과정을 계속 반복해야 위의 최적 정책을 얻을 수 있는데, 여기에서 꽤나 많은 계산량을 필요로 합니다. 그리고 $C$값은 $\gamma$값이 커질 때 같이 커집니다. 그런 경우에 굉장히 작은 보폭으로 최적화가 일어나기 때문에 시간이 많이 소요됩니다.

Trust Region Constraint

위의 MM 알고리즘에서 사용한 $\max_{\theta}[L_{\theta_{old}}({\theta}) - CD_{KL}^{max}(\theta_{old}, \theta)]$ 식을 아래와 같이 변형하겠습니다.

\[\max_{\theta} L_{\theta_{old}}(\theta) \space\space\space subject \space to \space \space\space D^{max}_{KL}(\theta_{old}, \theta) \leq \delta\]

위와 같이 변형한 식을 KL Constrained Objective라고 부릅니다. 원래 식에서는 $C$값에 의해 가능한 step의 크기가 결정되었는데, 여기에서는 $\delta$값을 통해 그 크기가 결정됩니다. 두 식은 최적화의 방식만 다를 뿐, 수학적으로 동일한 해에 도달하게 됩니다. 그런데 위 식에서 $\delta$값을 찾는 것도 쉬운 일이 아닙니다.

\[D^{max}_{KL}(\theta_{old}, \theta) = \max_sD_{KL}(\pi_{old}(\cdot | s) || \pi(\cdot | s)) \leq \delta\]

위의 식을 만족하는 $\delta$를 찾아야 하는데, 상태의 개수는 너무나도 많습니다. 심지어는 연속적인 상태인 경우도 있기 때문에 모든 상태에서 만족하는 $\delta$를 찾는 일은 정말 어렵습니다. 애초에 샘플 데이터를 사용하기 때문에 거의 불가능한 일입니다. 이런 문제를 해결하기 위해서 휴리스틱을 사용합니다.

Heuristic Approximation

\[\max_{\theta} L_{\theta_{old}}(\theta) \space\space\space subject \space to \space \space\space D^{max}_{KL}(\theta_{old}, \theta) \leq \delta\] \[\max_{\theta} L_{\theta_{old}}(\theta) \space\space\space subject \space to \space \space\space E_{s\sim\rho_{\theta_{old}}}[D_{KL}(\pi_{old}(\cdot | s) || \pi(\cdot | s))] \leq \delta\]

모든 상태 중 최댓값이 찾는게 아니라 위의 두 번째 식과 같이 평균만 $\delta$보다 작으면 되도록 합니다. 이렇게 식을 변형하면 샘플로 대체할 수 있게 됩니다. 이어서 Monte Carlo Simulation을 어떻게 사용하는지 설명합니다.

Monte Carlo Simulation

\[L_{\pi_{old}}(\pi)= \eta(\pi_{old}) + \sum_s\rho_{\pi_{old}}(s)\sum_a\pi(a|s) A_{\pi_{old}}(s, a)\] \[\max_{\theta} \sum_s\rho_{\pi_{old}}(s)\sum_a\pi_{\theta}(a|s) A_{\pi_{old}}(s, a) \space\space\space subject \space to \space \space\space E_{s\sim\rho_{\theta_{old}}}[D_{KL}(\pi_{old}(\cdot | s) || \pi(\cdot | s))] \leq \delta\]

위의 두 번재 식은 $L$을 첫 번째 식의 관계로 대체해 수정한 식입니다. $\eta(\pi_{old})$ 부분이 빠져있는데, 최댓값을 찾을 때는 상수 부분은 영향을 미치지 않기 때문에 제거한 것입니다. 뒤의 제약식은 샘플링으로 평균을 내면 되니까 문제가 되지 않는데, 앞의 목적함수 부분이 여전히 계산하기 어렵습니다. 따라서 아래와 같이 목적함수의 구성 요소들을 대체합니다.

\[\sum_s\rho_{\theta_{old}}(s) \rightarrow \frac{1}{1-\gamma}E_{s\sim \rho_{\theta_{old}}} \rightarrow E_{s\sim \rho_{\theta_{old}}}\]

• 상태 방문 빈도 함수가 확률이 될 수 있도록 $1-\gamma$를 곱하고 나눠 변형합니다.

\[A_{\theta_{old}} \rightarrow Q_{\theta_{old}}\]

• Advantage 함수 안에 숨어있는 상태 가치 함수는 어차피 상수이기 때문에 $\max$ 내에서는 있으나 없으나 동일하므로 제거합니다.

\[\sum_a\pi_{\theta}(a|s) A_{\theta_{old}}(s, a) \rightarrow E_{a\sim\pi_\theta}[A_{\theta_{old}}(s, a)] \rightarrow E_{a\sim\pi_{\theta_{old}}}[\frac{\pi_\theta(a|s)}{\pi_{\theta_{old}}(a|s)}A_{\theta_{old}}(s, a)]\]

• 다음 정책에서 샘플링할 수 없기 때문에 중요도 샘플링으로 식을 변형합니다.

\[\max_{\theta} E_{s\sim \rho_{\theta_{old}}, a\sim\pi_{\theta_{old}}}[\frac{\pi_\theta(a|s)}{\pi_{\theta_{old}}(a|s)}Q_{\theta_{old}}(s, a)] \space\space\space subject \space to \space \space\space E_{s\sim\rho_{\theta_{old}}}[D_{KL}(\pi_{old}(\cdot | s) || \pi(\cdot | s))] \leq \delta\]

결론적으로 위의 식을 얻게 됩니다. 식의 모든 구성이 현재 정책으로 이루어져있기 때문에 다음 정책을 어렵지 않게 계산할 수 있습니다. 실제로 MC를 사용한다면 아래의 과정을 거쳐 업데이트가 수행됩니다.

1. MC를 사용해 상태-행동 쌍, 궤적이 수집되고 Q 값이 추정됩니다(현재 정책에 따른 궤적).
2. 샘플이 적당히 수집되면 평균을 취해 목적 함수와 제약식의 값을 샘플들의 평균으로 추정합니다.
3. Natural Policy Gradient를 통해 제약 최적화를 수행하고 Line Search로 백트래킹을 수행합니다.

이런 과정들을 거쳐서 MC Simulation이 수행됩니다. Natural Policy Gradient는 우리에게 익숙한 adam같은 최적화 방법과 다른 2차 최적화 방법입니다. Natural Policy Gradient을 사용할 때 성능을 더 좋게 하기 위해 Conjugate Gradient를 함께 사용하게 됩니다. 아래에서 자세하게 살펴봅니다.

Natural Policy Gradient (NPG)

\[\max_{\theta} E_{s\sim \rho_{\theta_{old}}, a\sim\pi_{\theta_{old}}}[\frac{\pi_\theta(a|s)}{\pi_{\theta_{old}}(a|s)}Q_{\theta_{old}}(s, a)] \space\space\space subject \space to \space \space\space E_{s\sim\rho_{\theta_{old}}}[D_{KL}(\pi_{old}(\cdot | s) || \pi(\cdot | s))] \leq \delta\] \[\max_{\theta} L_{\theta_{old}}(\theta) \space\space\space subject \space to \space \space\space \bar D_{KL}(\theta_{old}||\theta) \leq \delta\]

MC에서 길게 풀어쓴 목적함수 식을 다시 위와 같이 간단하게 표현했습니다. 위의 식을 테일러 급수를 사용해서 근사를 하는데, 목적함수는 1차로 근사하고, 뒤의 제약식은 2차로 근사하면 아래와 같습니다.

목적함수와 제약식 모두 다 2차까지 테일러 근사를 수행합니다. 목적함수의 테일러 전개에서 상수항은 의미가 없기 때문에 날아가고($\max$에서 상수항은 영향이 없음), 2차항은 1차항에 비해 영향력이 굉장히 미미하기 때문에 생략합니다. 제약식의 경우 상수항과 1차항이 모두 0으로 날아가기 때문에 2차항만 남게 됩니다. 그래서 결과적으로 목적함수는 1차 미분식만을 사용하고 제약식은 2차 미분식만을 사용하게 됩니다.

\[\max_{\theta} \nabla_\theta L_{\theta_{old}}(\theta)|_{\theta=\theta_{old}}(\theta - \theta_{old}) \space\space\space subject \space to \space \space\space \frac{1}{2}(\theta - \theta_{old})^TH(\theta - \theta_{old}) \leq \delta\] \[H = \nabla^2_{\theta}\bar D_{KL}(\theta_{old}||\theta) = (\frac{\partial^2\bar D_{KL}(\theta_{old}||\theta)}{\partial\theta_i\partial\theta_j}|_{\theta = \theta_{old}})\]

$H$는 Hessian이라고 해서 이차 기울기(2nd Order Gradient)를 의미하고, Fisher Information Matrix라고 부릅니다.

\[\nabla_\theta f = \begin{bmatrix} \frac{\partial f}{\partial \theta_1} \\ \frac{\partial f}{\partial \theta_2} \\ \vdots \\ \frac{\partial f}{\partial \theta_n} \\ \end{bmatrix} \space\space\space\space\space \space\space\space\space\space \nabla^2_\theta f = \begin{bmatrix} \frac{\partial^2 f}{\partial \theta_i \partial \theta_j} \end{bmatrix}_{i, j}\]

위는 Gradient와 Hessian을 차례대로 나타낸 것인데, Hessian은 (n by n)의 크기를 가지는 행렬입니다. 때문에 Gradient에 비해서 필요한 계산량이 훨씬 많습니다.

\[H = \nabla^2_{\theta}\bar D_{KL}(\theta_{old}||\theta) = (\frac{\partial^2\bar D_{KL}(\theta_{old}||\theta)}{\partial\theta_i\partial\theta_j}|_{\theta = \theta_{old}})\] \[H \approx (\frac{1}{N}\sum_{n=1}^N\frac{\partial^2}{\partial\theta_i\partial\theta_j}D_{KL}(\pi_{old}(\cdot | s) || \pi(\cdot | s))|_{\theta = \theta_{old}})\]

실제로는 MC로 샘플링을 할 것이기 때문에 샘플들의 Hessian의 평균을 Fisher Information Matrix로 사용하게 됩니다.

\[\max_{\theta} \nabla_\theta L_{\theta_{old}}(\theta)|_{\theta=\theta_{old}}(\theta - \theta_{old}) \space\space\space subject \space to \space \space\space \frac{1}{2}(\theta - \theta_{old})^TH(\theta - \theta_{old}) \leq \delta\]

아무튼 간에 위의 식과 같이 정리가 됐습니다. 위 식을 업데이트 할 때 보통은 경사상승법을 사용하는데, 여기에서는 NPG를 사용해 업데이트합니다.

\[H^{-1}\nabla_{\theta}L_{\theta_{old}}(\theta)|_{\theta=\theta_{old}}\]

위 식이 NPG입니다. NPG는 일반 경사에 비해서 훨씬 더 최적점에 가까운 방향으로 업데이트를 수행하도록 도와줍니다. 왜 Hessian을 사용하는 NPG의 성능이 일반 경사보다 더 좋은지 아래에서 설명합니다.

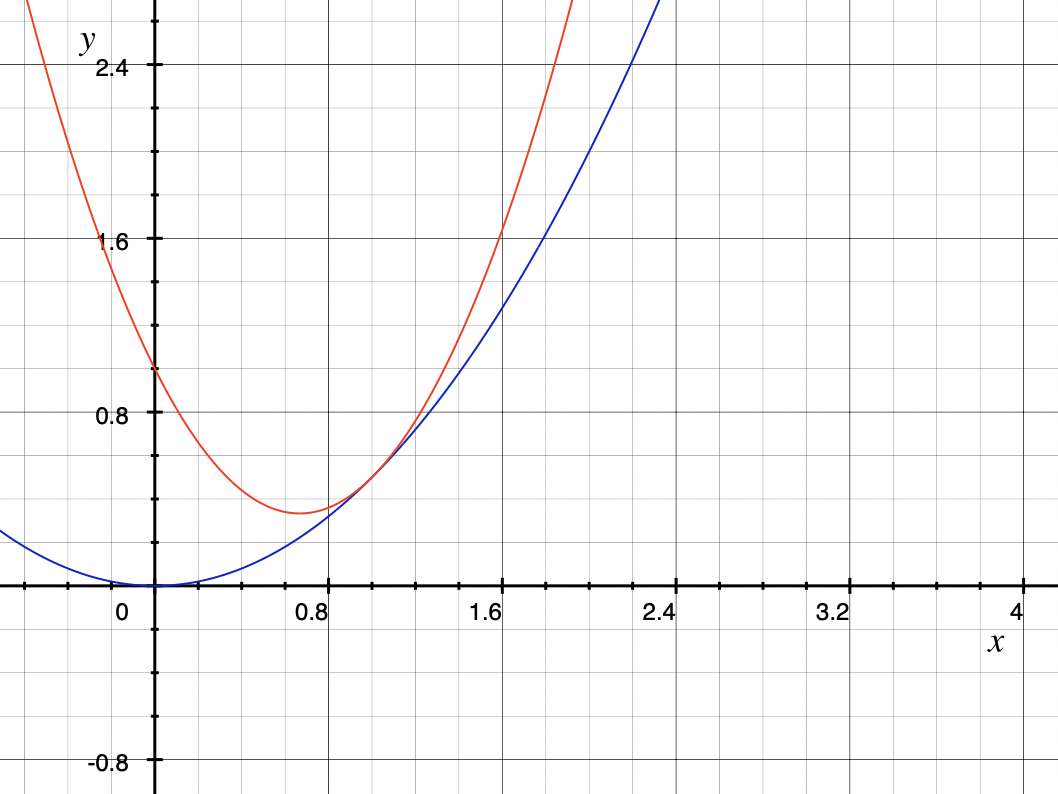
위 두 함수는 $x=1$에서 만납니다. 만나는 것 뿐만이 아니라 접하기 때문에 기울기 역시 동일합니다. 하지만 기울기의 변화량은 빨간색으로 나타난 함수에서 더 큽니다. 기울기의 변화량을 곡률(Cavature)라고 부릅니다. NPG는 이 곡률을 사용해서 경사 상승을 수행합니다. 이걸 사용하는게 왜 최적화에 도움이 되는지 아래에서 설명합니다.

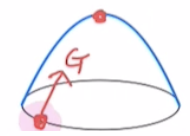
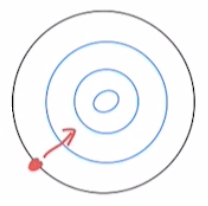
위와 같이 축 사이의 곡률 차가 크지 않은 경우에는 경사대로 올라가면 최적값에 곧바로 빠르게 가까워집니다.

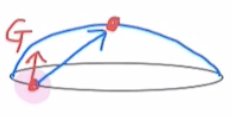
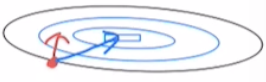
그런데 이렇게 축 사이에 곡률 차가 큰 경우에는 경사대로 올라가면 최적값에 바로 다가가지 않게 됩니다. 경사만 따지면 빨간색 화살표 방향이 가장 크지만 실제로는 파란색 화살표를 따라 업데이트 되었을 때 더 빠르게 최적값에 도달합니다. 따라서 축 별로 휘어진 정도를 앞에 곱해줘서 파란색 화살표를 따라 업데이트 되도록 하는 것, 이것을 Natural Gradient라고 합니다.

그런데 기존의 심층 강화학습에서는 이 Natural Gradient를 사용하는 경우가 없었습니다. Natural Gradient가 업데이트를 할 때는 정말 좋은데, 이걸 사용하기 위해서는 Hessian이 필요한데, Hessian을 계산하는 것은 정말 큰 계산량을 필요로하기 때문에 Natural Gradient가 사용되는 경우는 많지 않습니다. 그런데 TRPO에서는 어차피 근사시킨 최적화 식의 제약식 부분에서 Hessian이 필요하기 때문에 Hessian이 구해져 있습니다. 그래서 업데이트를 할 때 Hessian을 사용하는 NPG를 사용하게 되는 것입니다.

NPG를 통해서 다음 파라미터를 구한다면, 아래의 업데이트 식을 따르게 됩니다.

\[\theta = \theta_{old} + \beta \cdot H^{-1}\cdot g(gradient)\]

위 식에서 $\beta$는 업데이트의 step size인데, 이렇게 업데이트를 할 때 최적화 식의 제약식 조건에 위배되는지를 확인해야합니다.

\[\frac{1}{2}(\theta - \theta_{old})^TH(\theta - \theta_{old}) \leq \delta\] \[\frac{1}{2}(\beta\cdot H^{-1}\cdot g)^TH(\beta\cdot H^{-1}\cdot g) \leq \delta\]

위 식에서 $\beta$값이 최대가 되려면 우항과 좌항의 크기가 동일하면 됩니다. 그랬을 때의 $\beta$값은 아래와 같습니다.

\[\beta = \sqrt{\frac{2\delta}{g^T H^{-1}g}}\] \[\theta = \theta_{old} + \sqrt{\frac{2\delta}{g^T H^{-1}g}} \cdot H^{-1}\cdot g(gradient)\]

위의 식을 사용해서 업데이트를 하면 되긴 하는데, $H^{-1}$를 구하는게 여간 어려운 일이 아닙니다. 그런데 위 식을 살펴보면 $H^{-1}g$가 제곱근 안팎에서 동일하게 사용됩니다. 따라서 $H^{-1}g$을 한 번에 구하는 방향으로 생각해 보겠습니다.

\[x = H^{-1}g\] \[Hx = g\]

$H^{-1}g$를 구한다는 말은 $Hx = g$의 해를 구한다는 말과 동일합니다. 그리고 $Hx = g$는 Quadratic 함수이기 때문에 일반적인 경사하강법으로 구할 수 있습니다. 그런데, 여기서는 특별히 $H$가 Positive-Definite 행렬이기 때문에 Conjugate Gradient를 사용할 수 있습니다. Conjugate Gradient는 Gradient Descent보다 좀 더 적은 iteration 안에 해를 구할 수 있는 최적화 도구입니다. 비록 구현은 훨씬 복잡하긴 하지만 아무튼 TRPO에서는 이 Conjugate Gradient를 사용합니다.

이어서 Line Search라는 기법을 사용합니다. 여기까지 오는 과정에서 굉장히 많은 근사가 있었습니다. 때문에 위 식을 통해 구해진 $\beta$값이 정말 최대의 신뢰 구역인지 정확하게 알기 어렵습니다. 실제로 실험을 해보면 신뢰구간을 벗어나서 알고리즘의 성능이 훅 떨어지는 경우가 발생합니다. 이런 문제점을 극복하기 위해서 아래와 같이 0과 1 사이의 상수, $\alpha$를 곱해줍니다.

\[\beta \rightarrow \alpha\beta \space\space\space\space\space \space\space\space\space\space (0\lt\alpha \lt1)\]

0과 1 사이의 상수를 곱해줘서 신뢰 구역을 줄여주면 학습의 속도가 조금 줄어드는 대신에 안전한 학습을 이어갈 수 있습니다.

알고리즘

최종적인 TRPO 알고리즘 유사코드입니다. 먼저 정책 파라미터를 초기화하고 반복문을 돌게 됩니다. 반복문을 돌 때마다 새로운 정책을 얻게 되고, 이 과정을 반복해서 최적 정책에 도달하게 될 것입니다.

먼저 현재 정책에서 여러 궤적들을 수집합니다. 그리고 어떤 것이든 추정 알고리즘을 사용해서 Advantage(또는 Q)를 계산합니다. 이어서 Gradient와 Natural Gradient를 계산합니다. 이 값들을 이용해서 $\beta$값을 구해주고 Line Search까지 적용해 다음 정책을 구해줍니다.

TRPO는 신뢰 구역이라는 개념을 사용하면서 당시 상당한 성능을 보여준 알고리즘인데요, 몇 가지 단점들이 있습니다. TRPO는 1차 최적화가 아닌 2차 최적화를 사용하는데 이 방식은 Sample Efficiency가 다소 낮습니다. 그리고 Hessian 행렬을 구하는 것 자체에 굉장히 많은 컴퓨팅 자원이 필요합니다. 따라서 파라미터 수를 늘리는데 상당한 부담이 있습니다. 때문에 Deep CNNs나 RNNs에 적용하기 어렵다는 문제점이 있습니다.