강화학습 알고리즘: REINFORCE

이 포스팅은 ‘강화학습 알고리즘‘에 대한 내용을 담고 있습니다.

자료 출처: 단단한 강화학습, Reinforcement Learning An Introduction , 2nd edition. 리처드 서튼, 앤드류 바트로, 김성우(옮긴이), https://velog.io/@koyeongmin/REINFORCE-알고리즘>, https://github.com/seungeunrho/minimalRL

REINFORCE

REINFORCE 알고리즘은 정책 기반 강화학습 알고리즘입니다. 오랜 시간동안 강화학습에서는 가치 함수를 기반으로 정책을 선택하는 방식을 채택했습니다. 그러나 이 방식으로는 연속되는 상태공간을 가지는 문제를 풀기가 굉장히 어려웠습니다. 이 문제점의 해결책으로 가치함수를 파라미터화하는 아이디어가 제시되었는데요, REINFORCE 알고리즘에서는 가치함수를 파라미터화하는 것이 아니라 정책을 바로 내뱉는 함수를 파라미터로 표현합니다.

\[\pi_{\theta}(s) = a\]

이렇게 가치 함수를 기반으로 정책을 결정하는 것이 아니라, 정책 함수 자체를 업데이트하는 방식을 정책 기반 강화학습이라고 부릅니다. 그리고 정책 기반 강화학습 중에서도 몬테카를로 업데이트를 수행하는 알고리즘을 REINFORCE 알고리즘이라고 합니다. 수식들이 꽤나 복잡한데, 자세히 살펴보겠습니다.

행동 선택

REINFORCE 에서 행동의 선택은 파라미터화된 함수의 결과입니다. 그리고 궤적은 그러한 행동과 상태들의 나열이므로, 궤적은 파라미터화된 행동 선택 함수에 따르게 됩니다.

\[\pi_{\theta}(s) = a\] \[\tau \sim \pi_\theta\]

목적 함수

당연히 파라미터는 처음에 의미 없는 값으로 설정되기 때문에, 행동 선택 함수가 선택하는 행동은 정말 별로인 행동들일 것입니다. 이 파라미터를 적절한 값으로 업데이트하기 위해서는 우리가 원하는 목적을 수식으로 분명하게 명세해야 합니다.

에피소딕 문제에서 성능은 아래와 같이 정의됩니다.

\[J(\theta) \doteq v_{\pi_\theta}(s)\]

이제 위 수식에 대해서 경사도를 구해야 하는데요, 경사도를 구해서 $\theta \leftarrow \theta + \alpha \nabla J(\theta)$ 라는 업데이트 식(경사상승법)으로 파라미터를 수정합니다. 그런데 다행히도 $J(\theta)$의 경사도는 정책 경사도 정리에 의해 그 꼴이 간단하게 정리돼 있습니다.

\[\nabla J(\theta) \propto \sum_s \mu(s) \sum_a \nabla \pi(a|s) q_\pi (s, a)\]

• $\mu(s)$는 상태 $s$의 확률을 의미합니다. 실험적으로는 어떠한 상태든 상태를 방문한 횟수로 상태 $s$를 방문한 횟수를 나누어 구합니다.

그런데 우리는 여기서 정책을 근사할 것이기 때문에 $\pi$ 안에 $\theta$를 스윽 넣어주고 자리를 뒤로 빼줍니다.

\[\nabla J(\theta) \propto \sum_s \mu(s) \sum_a q_\pi (s, a)\nabla \pi(a|s, \theta)\]

$\sum_s \mu(s)$를 앞에 곱해준다는 것은 정책 $\pi$를 따를 때의 기댓값과 동일한 의미입니다. 따라서..

\[\nabla J(\theta) \propto E_\pi[ \sum_a q_\pi (S_t, a)\nabla \pi(a|S_t, \theta)]\]

• $s$ 대신에 $S_t$가 들어갔는데, 타임 스텝을 밟아갈 때 정책 $\pi$를 따르면서 상태들을 방문하기 때문입니다.
• 이어서 로그 미분 트릭을 적용해 식을 단순화시킵니다.

\[\nabla J(\theta) \propto E_\pi[ \sum_a \pi(a|S_t, \theta) \space q_\pi (S_t, a)\nabla \log \pi(a|S_t, \theta)]\] \[\nabla J(\theta) \propto E_\pi[ \space q_\pi (S_t, a)\nabla \log \pi(a|S_t, \theta)]\]

위 식에서 $q$함수가 사용됐는데, REINFORCE 알고리즘은 다른 말로 몬테카를로 정책 경사 알고리즘입니다. 몬테카를로 방법론에서는 여러 번의 에피소드를 통해 얻은 이득값을 사용해 상태 함수를 근사합니다. 때문에 $q$함수 자리에 $G_t$를 사용합니다.

\[\nabla J(\theta) \propto E_\pi[ \space G_t \nabla \log \pi(a|S_t, \theta)]\] \[\theta_{t+1} \doteq \theta_{t} + \alpha G_t\nabla \log \pi(a|S_t, \theta)\]

이로써 REINFORCE의 갱신 규칙을 얻게 되었습니다.

Baseline 적용

\[\nabla J(\theta) \propto E_\pi[ \sum_a q_\pi (S_t, a)\nabla\log\pi(a|S_t, \theta)]\]

위 식에서 아래와 같은 변형을 해도 괜찮습니다.

\[\nabla J(\theta) \propto E_\pi[ \sum_a (q_\pi (S_t, a) - b(s))\nabla \log \pi(a|S_t, \theta)]\]

정책에서 선택할 수 있는 행동 분포의 편미분은 모든 선택할 수 있는 모든 행동 대해서 그 합이 0입니다. 때문에 빼주는 값이 현재 상태에서 선택할 행동과 관련이 없는 함수라면 결과값에 영향을 주지 못합니다. 이렇게 특정 값을 빼주게 되면 갱신 기댓값이 갖는 분산에 큰 영향을 미치기 때문에 학습에 도움을 줄 수 있습니다.

알고리즘

구현된 알고리즘을 보면 위에서 계속 전개해 나갔던 수식이랑 모습이 사뭇 다른데요, 한 번에 업데이트할 지, 조금씩 업데이트할 지의 차이일 뿐 동일합니다.

파이썬 코드

아래는 파이썬에서 구현한 REINFORCE 알고리즘입니다.

import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Categorical
from torch.utils.tensorboard import SummaryWriter
import time  # 렌더링 시 잠깐씩 멈출 때 사용

writer = SummaryWriter(log_dir="logs/REINFORCE")

#Hyperparameters
learning_rate = 0.0002
gamma         = 0.98

class Policy(nn.Module):
    def __init__(self):
        super(Policy, self).__init__()
        self.data = []
        
        self.fc1 = nn.Linear(4, 128)
        self.fc2 = nn.Linear(128, 2)
        self.optimizer = optim.Adam(self.parameters(), lr=learning_rate)
        
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.softmax(self.fc2(x), dim=0)
        return x
      
    def put_data(self, item):
        self.data.append(item)
        
    def train_net(self):
        R = 0
        self.optimizer.zero_grad()
        for r, prob in self.data[::-1]:
            R = r + gamma * R
            loss = -torch.log(prob) * R
            loss.backward()
        self.optimizer.step()
        self.data = []

def main():
    env = gym.make('CartPole-v1')
    pi = Policy()
    score = 0.0
    print_interval = 20
    
    
    for n_epi in range(3000):
        s, _ = env.reset()
        done = False
        
        while not done: # CartPole-v1 forced to terminates at 500 step.
            prob = pi(torch.from_numpy(s).float())
            m = Categorical(prob)
            a = m.sample()
            s_prime, r, done, truncated, info = env.step(a.item())
            pi.put_data((r,prob[a]))
            s = s_prime
            score += r
            
        pi.train_net()
        
        if n_epi%print_interval==0 and n_epi!=0:
            writer.add_scalar('score', score/print_interval, n_epi)
            print("# of episode :{}, avg score : {}".format(n_epi, score/print_interval))
            score = 0.0
    # ---------- 학습이 끝난 뒤, 렌더링 테스트 ----------
    print("Training completed. Now testing (rendering) the final policy...")
    # CartPole 환경 재생성을 권장 (render_mode='human' 가능, 하지만 Gym 버전에 따라 다름)

    writer.close()  # 텐서보드 끄기
    env.close()  # 기존 env 닫고
    env = gym.make('CartPole-v1', render_mode='human')  # 다시 생성
    for test_ep in range(5):  # 5 에피소드 정도 시각화
        s, _ = env.reset()
        done = False
        ep_score = 0.0
        while not done:
            env.render()
            time.sleep(0.01)  # 속도를 너무 빠르게 하고 싶지 않다면 잠깐 딜레이
            prob = pi(torch.from_numpy(s).float())
            m = Categorical(prob)
            a = m.sample().item()
            s, r, done, truncated, info = env.step(a)
            ep_score += r
        print(f"Test Episode {test_ep+1} Score: {ep_score:.1f}")
    env.close()

if __name__ == '__main__':
    main()

코드가 꽤나 긴데, REINFORCE 알고리즘의 핵심이 되는train부분을 집중적으로 살펴보겠습니다.

    def train_net(self):
        R = 0
        self.optimizer.zero_grad()
        for r, prob in self.data[::-1]:
            R = r + gamma * R
            loss = -torch.log(prob) * R
            loss.backward()
        self.optimizer.step()
        self.data = []

코드를 보면, 하나의 에피소드가 진행되는 동안에는 학습이 수행되지 않고, 에이전트가 받은 보상과 에이전트가 선택한 행동의 정책 확률을 저장합니다. 그리고 REINFORCE 알고리즘의 아래 수식에 해당하는 값을 반복 계산합니다.

\[\theta_{t+1} \doteq \theta_{t} + \alpha G_t\nabla \log \pi(a|S_t, \theta)\]

모든 궤적에 대해서 기울기를 구했으면 마지막에 한 번에 업데이트를 수행합니다. 위에서 설명했던 수식과 다르게 코드에서는 loss = -torch.log(prob) * R 로 음수 기호가 붙는데요, 이는 경사하강이 아닌 경사상승을 해야하기 때문입니다. Pytorch를 포함하는 대부분의 라이브러리는 기본적으로 경사하강을 하는 상황을 가정하기 때문에 음수 기호를 붙혀줘 보상을 최대화하도록 업데이트합니다.

학습 결과

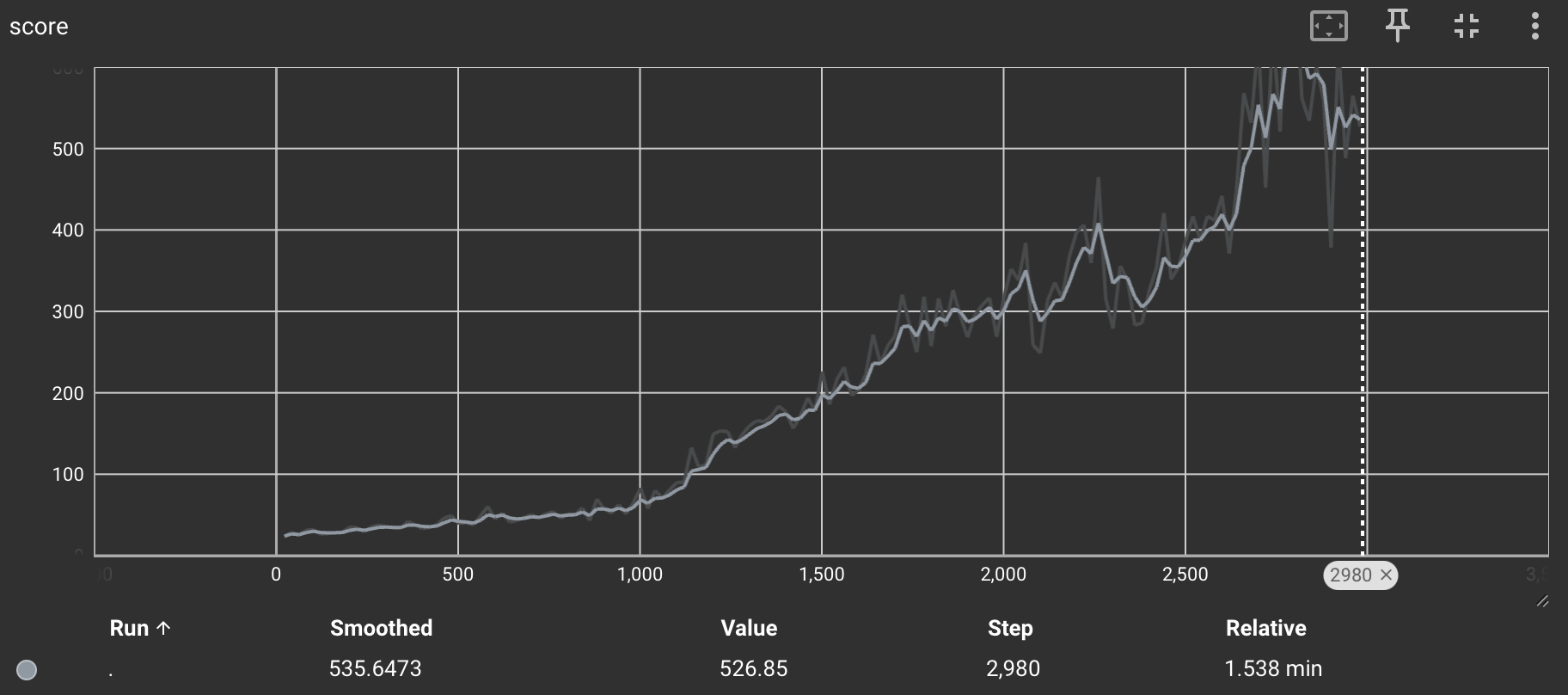
실제로 학습을 시켜보면 꾸준히 성능이 오르는 것을 확인할 수 있습니다. 아래는 테스트 렌더링 결과입니다.