강화학습 알고리즘: DQN(Deep Q Network)
이 포스팅은 ‘강화학습 알고리즘‘에 대한 내용을 담고 있습니다.
자료 출처: 단단한 강화학습, Reinforcement Learning An Introduction , 2nd edition. 리처드 서튼, 앤드류 바트로, 김성우(옮긴이)>, https://github.com/seungeunrho/minimalRL, EE488D: Introduction to Reinforcement Learning Spring 2023. Donghwan Lee. KAIST EE
DQN
DQN(Deep Q Network)은 Q-learning에서 Q함수를 테이블 형식이 아니라 NN을 사용해 성공적으로 학습시킨 첫 번째 알고리즘입니다. 사실 당시에 이미 많은 사람들이 DNN을 사용한 Q-learning을 시도하고 있었습니다. 하지만 대다수의 Deep Q-learning은 성공적이지 못했고, 그마저도 다양한 테스크에 적용하기는 어려운 모델들이 전부였습니다. Deepmind에서 공개한 DQN은 DNN을 Q-learning과 함께 사용할 때 발생하는 문제점들을 효과적으로 극복합니다.
Q 근사 함수
\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma \space \underset{a}max\space Q(S_{t+1}, a) - Q(S_t, A_t)]\]Q 함수를 최적화할 때 사용되는 위 수식(Q-learning)은 수렴성이 보장된다는 큰 이점이 존재합니다. 그런데 위의 식으로 업데이트를 하려면 모든 상태, 행동 쌍에 대한 표를 저장하고 있어야 합니다. 이러한 방법으로 접근하면 간단한 보드게임에서 조차 큰 어려움을 겪게 됩니다. 하물며, 연속적인 상태를 가지는 문제는 접근조차 할 수 없습니다. 무수히 많은 상태공간으로 인해 발생하는 문제점들을 해결하는 좋은 방법이 있는데요, 바로 근사 함수를 사용하는 것입니다.
\(Q(S_t, A_t|\theta) \leftarrow Q(S_t, A_t|\theta) + \alpha[R_{t+1} + \gamma \space \underset{a}max\space Q(S_{t+1}, a|\theta) - Q(S_t, A_t|\theta)]\) 위와 같이 파라미터화를 한 Q 함수를 사용하면 더 이상 모든 상태 행동 쌍의 값을 저장할 필요가 없어집니다. 그리고 Q 근사 함수는 겪어보지 못한 상태의 이득을 예측할 수 있는 일반화 능력을 갖습니다.
Deep Q-learning의 문제점
\(R_{t+1} + \gamma \space \underset{a}max\space Q(S_{t+1}, a|\theta) - Q(S_t, A_t|\theta)\) 그러면 위의 TD-error를 loss로 사용하고 편미분을 취해서 인공신경망을 최적화하면 되겠네요? 수많은 사람들이 그렇게 생각했고 도전했는데요, 사실 결과는 썩 그리 좋지 않았습니다. 이유는 인공신경망의 이론적 특성에 있습니다. 인공신경망은 데이터가 서로 독립이라는 가정 아래 학습합니다. 하지만, 강화학습에서 수집하는 데이터들은 연속적인 행동으로 얻어지기 때문에 데이터들이 서로 큰 연관성을 가지게 됩니다.
그리고 또 다른 문제점이 있는데요, 인공신경망이 학습하는 목표가 움직이는(Moving Target) 문제점이 발생합니다. 우리가 보통 신경망을 학습시킬 때 대부분 지도학습을 사용합니다. 지도학습은 고정된 정답지이고, 그 고정된 목표를 향해서 인공신경망은 조금씩 최적화됩니다. 그런데 강화학습에서는 그렇지 않습니다.
\[R_{t+1} + \gamma \space \underset{a}max\space Q(S_{t+1}, a|\theta)\]강화학습에서 정답지로 사용하는 위의 TD-target은 인공신경망이 학습하는 순간순간마다 그 값이 달라지게 됩니다. 식 자체의 의미가 ‘신경망이 생각하는 그 다음 상태의 가치’이기 때문에 신경망이 변화하면 목표가 이동하게 됩니다. 때문에 학습 불안정성이 유발되고 신경망 학습이 잘 수행되지 못하게 됩니다.
Replay Buffer
DQN에서는 데이터 사이의 연관성을 줄이기 위해 Replay Buffer를 사용합니다. DQN 알고리즘에서는 에피소드를 진행하면서 얻는 궤적 정보를 바로 학습하지 않습니다. 대신에 Replay Buffer에 일단 저장합니다. 그리고 미리 설정해 둔 특정 수 이상의 상태-행동 쌍이 쌓이면, 그때부터 학습을 시작합니다. 이 때 상태-행동 쌍이 수집된 순서대로 학습을 하는 것이 아니라, 랜덤으로 배치 수만큼을 추출해서 학습을 수행합니다. 이렇게 하면, 뽑히는 상태-행동 쌍들이 같은 에피소드이거나, 연속된 순서일 가능성이 낮아지기 때문에 샘플들 간의 연관성이 하락합니다.
Target Q Network
이어서 DQN에서는 움직이는 목표 문제를 해결하기 위해서 고정된 Target Q Network를 사용합니다. Target Network라는 아이디어는 Double Q-Learning에서 온 것인데, Double Q-Learning에서는 과추정 문제를 해결하기 위해서 2개의 Q함수를 사용합니다. DQN에서도 유사하게 Target값을 추정하는 네트워크와 행동을 선택하는 네트워크를 분리시킵니다.
\[R_{t+1} + \gamma \space \underset{a}max\space Q(S_{t+1}, a|\theta_{frozen})\]위 식은 TD-target을 계산하기 위한 식입니다. Q 네트워크가 학습할 때 위의 값이 계속 변하는게 문제가 되는건데요, 이 문제를 해결하기 위해 위의 TD-target을 계산하는 Q 네트워크를 별도로 선언합니다. 그렇게 따로 선언된 네트워크를 Target Q Network라고 부르는데, Target Q Network는 기본적으로 Q 네트워크와 동일한 파라미터 값을 가집니다. 그런데, 항상 동일한 파라미터를 가지는게 아니라, 조금 늦게 따라오도록 파라미터를 업데이트합니다.
예를 들어서, Q 네트워크가 100번의 업데이트가 수행되었다면, Target Q Network는 50번에 한 번 씩 Q 네트워크와 파라미터를 동일하게 맞춰줍니다. 이런 식으로 Target Q Network를 업데이트하면 Q 네트워크의 목표 대상이 50회의 업데이트동안 고정된 상태를 유지하기 때문에 학습이 훨씬 안정적이게 됩니다.
알고리즘

위 사진이 DQN의 알고리즘입니다. Replay Buffer 아이디어가 사용된 것을 확인할 수 있는데, Target Q Network가 사용된 것인지는 알고리즘에 명확하게 드러나지 않은 것 같습니다. 하지만 논문에서 정의된 손실함수를 보면 이전 iteration의 파라미터를 사용해 TD-target을 계산한다고 분명하게 표현돼 있습니다.
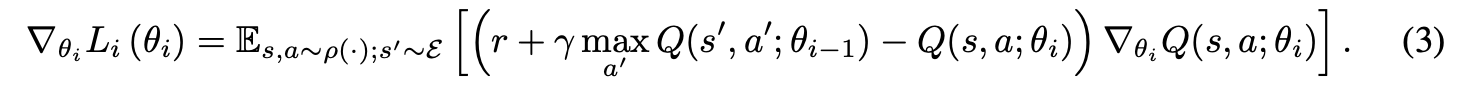
파이썬 코드
import gym
import collections
import random
import time
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter("logs/dqn")
#Hyperparameters
learning_rate = 0.0005
gamma = 0.98
buffer_limit = 50000
batch_size = 32
class ReplayBuffer():
def __init__(self):
self.buffer = collections.deque(maxlen=buffer_limit)
def put(self, transition):
self.buffer.append(transition)
def sample(self, n):
mini_batch = random.sample(self.buffer, n)
s_lst, a_lst, r_lst, s_prime_lst, done_mask_lst = [], [], [], [], []
for transition in mini_batch:
s, a, r, s_prime, done_mask = transition
s_lst.append(s)
a_lst.append([a])
r_lst.append([r])
s_prime_lst.append(s_prime)
done_mask_lst.append([done_mask])
return torch.tensor(s_lst, dtype=torch.float), torch.tensor(a_lst), \
torch.tensor(r_lst), torch.tensor(s_prime_lst, dtype=torch.float), \
torch.tensor(done_mask_lst)
def size(self):
return len(self.buffer)
class Qnet(nn.Module):
def __init__(self):
super(Qnet, self).__init__()
self.fc1 = nn.Linear(4, 128)
self.fc2 = nn.Linear(128, 128)
self.fc3 = nn.Linear(128, 2)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def sample_action(self, obs, epsilon):
out = self.forward(obs)
coin = random.random()
if coin < epsilon:
return random.randint(0,1)
else :
return out.argmax().item()
def train(q, q_target, memory, optimizer):
for i in range(10):
s,a,r,s_prime,done_mask = memory.sample(batch_size)
q_out = q(s)
q_a = q_out.gather(1,a) # action에 해당하는 q-value만 골라냄
max_q_prime = q_target(s_prime).max(1)[0].unsqueeze(1)
target = r + gamma * max_q_prime * done_mask
loss = F.smooth_l1_loss(q_a, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
def main():
env = gym.make('CartPole-v1')
q = Qnet()
q_target = Qnet()
q_target.load_state_dict(q.state_dict())
memory = ReplayBuffer()
print_interval = 20
score = 0.0
optimizer = optim.Adam(q.parameters(), lr=learning_rate)
for n_epi in range(1000):
epsilon = max(0.01, 0.08 - 0.01*(n_epi/200)) #Linear annealing from 8% to 1%
s, _ = env.reset()
done = False
epi_score = 0
while not done:
a = q.sample_action(torch.from_numpy(s).float(), epsilon)
s_prime, r, done, truncated, info = env.step(a)
done_mask = 0.0 if done else 1.0
memory.put((s,a,r/100.0,s_prime, done_mask))
s = s_prime
score += r
epi_score += r
if done or epi_score >=10000:
break
if memory.size()>2000:
train(q, q_target, memory, optimizer)
if n_epi%print_interval==0 and n_epi!=0:
q_target.load_state_dict(q.state_dict())
writer.add_scalar("score", score/print_interval, n_epi)
print("n_episode :{}, score : {:.1f}, n_buffer : {}, eps : {:.1f}%".format(
n_epi, score/print_interval, memory.size(), epsilon*100))
score = 0.0
env.close()
writer.close()
# ---------- 학습이 끝난 뒤, 렌더링 테스트 ----------
print("Now testing (rendering) the final policy...")
# render_mode='human' 으로 재생성
env_render = gym.make('CartPole-v1', render_mode='human')
# 테스트 에피소드 횟수 설정
test_episodes = 3
for ep in range(test_episodes):
s, _ = env_render.reset()
done = False
episode_score = 0.0
# 테스트 시에는 epsilon=0 (greedy)
while not done:
a = q.sample_action(torch.from_numpy(s).float(), epsilon=0.0)
s, r, done, truncated, info = env_render.step(a)
episode_score += r
# 딜레이
time.sleep(0.01)
print(f"[Test Episode {ep+1}] Score: {episode_score:.1f}")
# 대기
time.sleep(1.0)
# 테스트 환경 종료
env_render.close()
if __name__ == '__main__':
main()
위는 DQN의 파이썬 코드입니다. 아래에서 train 부분을 자세하게 살펴보겠습니다.
def train(q, q_target, memory, optimizer):
for i in range(10):
s,a,r,s_prime,done_mask = memory.sample(batch_size)
q_out = q(s)
q_a = q_out.gather(1,a) # action에 해당하는 q-value만 골라냄
max_q_prime = q_target(s_prime).max(1)[0].unsqueeze(1)
target = r + gamma * max_q_prime * done_mask
loss = F.smooth_l1_loss(q_a, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
s,a,r,s_prime,done_mask = memory.sample(batch_size) 라고 돼있는 부분이 Replay Buffer를 사용하는 코드입니다. DQN에서 에피소드를 돌면서 memory라는 덱(deque)에 상태-행동 쌍을 저장합니다. 그리고 학습을 할 때 배치 크기만큼 랜덤으로 추출합니다.
if n_epi%print_interval==0 and n_epi!=0:
q_target.load_state_dict(q.state_dict())
writer.add_scalar("score", score/print_interval, n_epi)
print("n_episode :{}, score : {:.1f}, n_buffer : {}, eps : {:.1f}%".format(
n_epi, score/print_interval, memory.size(), epsilon*100))
score = 0.0
위는 중간중간에 로그를 표시하는 코드블럭입니다. 20번 에피소드를 돌 때마다 q_target.load_state_dict(q.state_dict())으로 업데이트하도록 설정된 것을 확인할 수 있습니다.
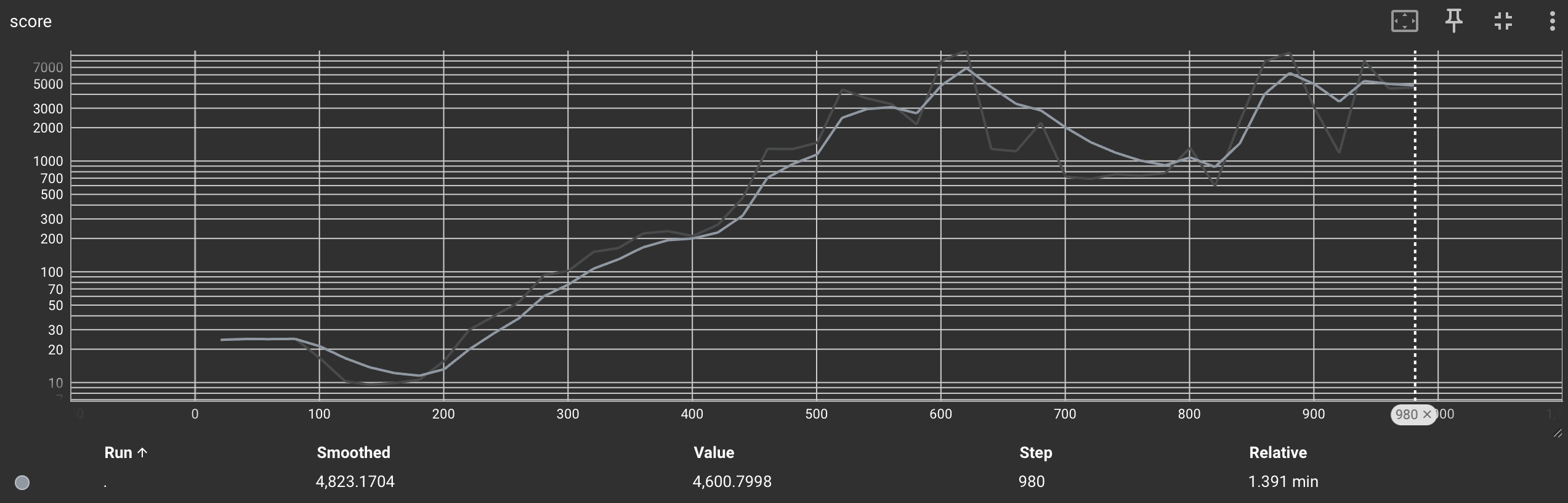
위 그림은 Cartpole-V1에서 DQN을 학습시킨 결과인데요, 학습 성능이 꽤나 준수한 것을 확인할 수 있습니다. 아래는 테스트 렌더링 결과입니다.
DQN with Dueling Architecture
DQN with Dueling Architecture에서는 Q값을 추정하기 위해, V함수와 Advantage함수를 이용합니다.
\[Q_{\theta}(s, a) = V_\theta(s) + A_\theta(s, a)\]위 식에서 V함수는 Long-term effect를, Advantage함수는 ‘당장 선택할 수 있는 행동들 중 무엇이 가장 가치있는가?‘를 의미합니다. 두 부분을 분리했을 때 보다 안정적으로 학습할 수 있습니다. 그런데 위의 식을 그대로 사용하기는 조금 어렵습니다. 우리가 식을 만들 때에는 V함수가 가치 함수로 학습되고 Advantage함수가 Advantage가 학습되도록 바라고 만들었지만, 실제로도 그렇게 학습되리라는 보장은 없습니다. 동일한 값을 더하고 빼주어도 어차피 Q함수는 변하지 않기 때문에 우리가 원하는 대로 학습이 되지 않을 가능성이 높습니다. 이를 해결하기 위해서 아래와 같이 기준점을 잡아줍니다.
\[Q_{\theta}(s, a) = V_\theta(s) + A_\theta(s, a) - \max_uA_{\theta}(s, u)\]위와 같이 Advantage 중 최댓값을 제하면 Advantage 값의 최댓값은 0으로 고정됩니다. 따라서 신경망이 학습될 때 의미적으로 보다 분명하게 분리할 수 있습니다. 위 식에서 Q함수와 V함수, 그리고 A함수까지 최적에 도달했을 때에도 등식이 성립하기 때문에 그대로 사용하기에 문제가 없습니다. 실제로는 보다 안정적인 학습을 위해 아래와 같이 최댓값을 대신해 평균값을 제합니다.
\[Q_{\theta}(s, a) = V_\theta(s) + A_\theta(s, a) - \frac{1}{|A|}\sum_{u \in A}A_{\theta}(s, u)\]위의 수식이 바로 DQN with Dueling Architecture에서 Q값을 구하는 수식입니다. Q함수를 추정하는 방식에 관한 것이기 때문에 다른 방법론과 결합해서 사용할 수 있는데, Double Deep Q-Learning과 함께 Deuling Architecture를 사용하는 알고리즘을 D3QN이라고 부릅니다.
파이썬 코드
class DDQN(torch.nn.Module):
def __init__(self):
super().__init__()
self.fc = torch.nn.Linear(4, 64)
self.fcV1 = torch.nn.Linear(64, 64)
self.fcA1 = torch.nn.Linear(64, 64)
self.fcV2 = torch.nn.Linear(64, 1)
self.fcA2 = torch.nn.Linear(64, 2)
def forward(self, x):
x = self.fc(x)
x = torch.nn.functional.relu(x)
V = self.fcV1(x)
V = torch.nn.functional.relu(V)
V = self.fcV2(V)
A = self.fcA1(x)
A = torch.nn.functional.relu(A)
A = self.fcA2(A)
return V + A - A.mean(dim=-1, deepdims=True) # Dueling Architecture
코드를 보면 Advantage함수의 평균값을 빼주는 부분을 가장 마지막 줄에서 확인할 수 있습니다.
댓글남기기