강화학습 알고리즘: DDPG(Deep Deterministic Policy Gradient)
이 포스팅은 ‘강화학습 알고리즘‘에 대한 내용을 담고 있습니다.
자료 출처: 단단한 강화학습, Reinforcement Learning An Introduction , 2nd edition. 리처드 서튼, 앤드류 바트로, 김성우(옮긴이), https://www.youtube.com/watch?v=Ukloo2xtayQ, https://github.com/seungeunrho/minimalRL>
DDPG(Deep Deterministic Policy Gradient)
DDPG(Deep Deterministic Policy Gradient)은 구글의 딥마인드 팀에서 DQN에 이어 제안한 또 다른 정책 경사 알고리즘입니다. DQN에서 여러 테크닉과 함께 인공 신경망을 사용함으로써 입력이 연속적인 도메인인 경우를 성공적으로 해결할 수 있었지만, 출력이 연속적인 도메인인 경우는 DQN이 다루지 못합니다. DQN의 출력노드가 곧 에이전트의 행동이 되는데 이걸 어떻게 연속적인 도메인과 맞출 수 있을 지 방법이 잘 떠오르지 않는데요, DDPG에서 이 물음에 대한 해결책을 제시합니다.
DPG(Deterministic Policy Gradient)
DDPG라는 이름을 통해 DPG가 이전에 있지 않았을까 짐작할 수 있는데요, 실제로 DDPG는 DPG에서 발전돼서 만들어진 알고리즘입니다. DPG알고리즘에 대해서 먼저 살펴보고 이어서 DDPG 알고리즘에 대해 자세히 다룹니다.
DPG란 결정론적(Deterministic) 정책을 사용하는 정책 경사 알고리즘입니다.
\[a = \mu(s)\]위와 같이 상태를 받으면, 행동을 툭 뱉는 형태로 설계됩니다. 물론 DPG에서도 비평가(Critic)가 존재합니다. 비평가는 주어진 상태와 행동 쌍을 평가하기 때문에 함수의 입력에 상태와 행동이 둘다 필요한데요, 위의 결정론적 행동 선택 함수를 가져다가 사용하면 됩니다.
\[Q(s, \mu(s))\]DPG 알고리즘은 신경망이 상태를 받고 행동을 결정론적으로 반환하는 형태이기 때문에 연속적인 행동 공간을 가지는 문제를 해결할 수 있습니다. 이렇게 행동 선택 함수가 결정론적인 경우에도 경사 하강 정리가 이미 만들어져 있는데, 아래와 같습니다.
\[\Delta\theta = \nabla_aQ^u(s, a)|_{a=\mu_\theta(s)}\nabla_\theta\mu_\theta(s)\]위의 식을 사용해서 결정론적 행동 선택함수의 파라미터를 최적화할 수 있습니다. DDPG 알고리즘은 DPG 알고리즘의 결정론적 행동 선택 함수와 함께 행동 비평가 알고리즘의 구조와 DQN의 아이디어까지 모두 사용합니다.
DDPG
DDPG는 DQN의 핵심 아이디어인 Replay Buffer와 Target Network를 사용합니다. $Q$에 대한 손실함수는 아래와 같습니다.
\[L(\phi) = E_{s\sim\rho_\mu}[(r + \gamma \hat Q_{\hat\phi}(s', \hat\mu_{\hat\theta}(s')) - Q_\phi(s, a))^2]\]위의 손실함수에서 눈여겨 봐야하는 부분은 TD-Target을 계산할 때 결정론적 행동함수 역시 마찬가지로 Target Network를 사용한다는 점입니다. Target Network는 지연되는 업데이트가 수행되는데 그 과정에서 선택되는 행동은 계속 조금씩의 차이가 존재할 가능성이 높습니다. 비평가의 목표는 상태를 정확하게 평가하는 것이기 때문에 손실함수가 MSE의 형태입니다.
아무튼 위 식에 미분을 취해서 $\phi$를 업데이트하는데, 기울기는 아래와 같이 나옵니다.
\[-\Delta\phi = (r + \gamma \hat Q_{\hat\phi}(s', \hat\mu_{\hat\theta}(s')) - Q_\phi(s, a))\nabla_\phi Q_\phi(s, a)\]마찬가지로 $\mu$에 대한 목적함수와 기울기는 아래와 같습니다.
\[J(\theta) = E_{s\sim\rho_\mu}[Q_\phi(s, a)] \rvert_{a=\mu_\theta(s)}\] \[\Delta\theta = \nabla_a Q_\phi(s, a) \rvert_{a=\mu_\theta(s)} \nabla_\theta\mu_\theta(s)\]DDPG는 DQN과 다르게 한 가지 문제점이 있습니다. 바로 탐험(Exploration)이 좀처럼 수행되지 않는다는 점인데요, DQN의 경우 확률론적 정책을 사용하기 때문에 어느정도의 탐험을 보장합니다. 하지만 DDPG와 같이 결정론적 정책을 사용하면 탐험을 전혀 수행하지 않기 때문에 탐험을 수행할 수 있도록 에이전트를 강제해야 합니다.
사실 DQN의 확률론적 정책이 자체로 탐험을 포함함에도 $\epsilon$ - 탐욕적 행동 선택을 하도록 알고리즘에 포함되어 있는데요, DDPG에도 마찬가지로 이런 식의 랜덤성을 추가해줍니다. 다만 추가하는 방식이 조금 다릅니다. DQN의 경우 행동의 수 자체가 많지 않기 때문에 나머지 행동들에 대해서 동일한 확률로 뽑는 탐험을 수행할 수 있었지만, DDPG가 돌아가는 연속 행동 공간에서는 큰 의미를 가지기 어렵습니다. 때문에 모든 행동을 랜덤으로 탐험하는 방법이 아니라, 에이전트가 선택한 행동에 노이즈를 추가하는 방식으로 탐험을 수행합니다.
\[\mathcal{N}: a_t = \mu_\theta(s_t) + \mathcal{N_t}\]위의 가우시안 노이즈를 에이전트의 행동 선택에 추가해 에이전트가 탐험을 지속적으로 수행하도록 만들어줍니다. 모든 타임 스텝에 동일한 노이즈를 추가하기보다는 타임 스텝별로 다른 가우시안 노이즈를 추가해, 좀 더 세밀한 탐험을 수행하도록 합니다.
\[\hat \phi \leftarrow \tau \phi + (1 - \tau) \hat \phi\] \[\hat \theta \leftarrow \tau \theta + (1 - \tau) \hat \theta\]추가로 DQN에서와 다르게 Target Network를 업데이트하는 방식이 조금 다릅니다. DQN에서는 특정 Iteration에서 동일하게 업데이트하는 방식이었는데요, 여기에서는 EWMA 방식으로 업데이트하는 Soft Update 방식을 사용합니다.
알고리즘

Replay Buffer와 Target Network, Actor-Critic구조, 그리고 Soft Update까지 알고리즘에서 확인할 수 있습니다.
파이썬 코드
import gym
import random
import collections
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import time
from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter("logs/ddpg")
#Hyperparameters
lr_mu = 0.0005
lr_q = 0.001
gamma = 0.99
batch_size = 32
buffer_limit = 50000
tau = 0.005 # for target network soft update
class ReplayBuffer():
def __init__(self):
self.buffer = collections.deque(maxlen=buffer_limit)
def put(self, transition):
self.buffer.append(transition)
def sample(self, n):
mini_batch = random.sample(self.buffer, n)
s_lst, a_lst, r_lst, s_prime_lst, done_mask_lst = [], [], [], [], []
for transition in mini_batch:
s, a, r, s_prime, done = transition
s_lst.append(s)
a_lst.append([a])
r_lst.append([r])
s_prime_lst.append(s_prime)
done_mask = 0.0 if done else 1.0
done_mask_lst.append([done_mask])
return torch.tensor(s_lst, dtype=torch.float), torch.tensor(a_lst, dtype=torch.float), \
torch.tensor(r_lst, dtype=torch.float), torch.tensor(s_prime_lst, dtype=torch.float), \
torch.tensor(done_mask_lst, dtype=torch.float)
def size(self):
return len(self.buffer)
class MuNet(nn.Module):
def __init__(self):
super(MuNet, self).__init__()
self.fc1 = nn.Linear(3, 128)
self.fc2 = nn.Linear(128, 64)
self.fc_mu = nn.Linear(64, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
mu = torch.tanh(self.fc_mu(x))*2 # Multipled by 2 because the action space of the Pendulum-v0 is [-2,2]
return mu
class QNet(nn.Module):
def __init__(self):
super(QNet, self).__init__()
self.fc_s = nn.Linear(3, 64)
self.fc_a = nn.Linear(1,64)
self.fc_q = nn.Linear(128, 32)
self.fc_out = nn.Linear(32,1)
def forward(self, x, a):
h1 = F.relu(self.fc_s(x))
h2 = F.relu(self.fc_a(a))
cat = torch.cat([h1,h2], dim=1)
q = F.relu(self.fc_q(cat))
q = self.fc_out(q)
return q
class OrnsteinUhlenbeckNoise:
def __init__(self, mu):
self.theta, self.dt, self.sigma = 0.1, 0.01, 0.1
self.mu = mu
self.x_prev = np.zeros_like(self.mu)
def __call__(self):
x = self.x_prev + self.theta * (self.mu - self.x_prev) * self.dt + \
self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape)
self.x_prev = x
return x
def train(mu, mu_target, q, q_target, memory, q_optimizer, mu_optimizer):
s,a,r,s_prime,done_mask = memory.sample(batch_size)
target = r + gamma * q_target(s_prime, mu_target(s_prime)) * done_mask
q_loss = F.smooth_l1_loss(q(s,a), target.detach())
q_optimizer.zero_grad()
q_loss.backward()
q_optimizer.step()
mu_loss = -q(s,mu(s)).mean() # That's all for the policy loss.
mu_optimizer.zero_grad()
mu_loss.backward()
mu_optimizer.step()
def soft_update(net, net_target):
for param_target, param in zip(net_target.parameters(), net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - tau) + param.data * tau)
def main():
env = gym.make('Pendulum-v1', max_episode_steps=200, autoreset=True)
memory = ReplayBuffer()
q, q_target = QNet(), QNet()
q_target.load_state_dict(q.state_dict())
mu, mu_target = MuNet(), MuNet()
mu_target.load_state_dict(mu.state_dict())
score = 0.0
print_interval = 20
mu_optimizer = optim.Adam(mu.parameters(), lr=lr_mu)
q_optimizer = optim.Adam(q.parameters(), lr=lr_q)
ou_noise = OrnsteinUhlenbeckNoise(mu=np.zeros(1))
for n_epi in range(3000):
s, _ = env.reset()
done = False
count = 0
while count < 200 and not done:
a = mu(torch.from_numpy(s).float())
a = a.item() + ou_noise()[0]
s_prime, r, done, truncated, info = env.step([a])
memory.put((s,a,r/100.0,s_prime,done))
score +=r
s = s_prime
count += 1
if memory.size()>2000:
for i in range(10):
train(mu, mu_target, q, q_target, memory, q_optimizer, mu_optimizer)
soft_update(mu, mu_target)
soft_update(q, q_target)
if n_epi%print_interval==0 and n_epi!=0:
writer.add_scalar("score", score/print_interval, n_epi)
print("# of episode :{}, avg score : {:.1f}".format(n_epi, score/print_interval))
score = 0.0
env.close()
writer.close()
# ---------- 학습이 끝난 뒤, 렌더링 테스트 ----------
print("Now testing (rendering) the final policy...")
# render_mode='human' 으로 재생성
env_render = gym.make('Pendulum-v1', render_mode='human')
# 테스트 에피소드 횟수 설정
test_episodes = 3
for ep in range(test_episodes):
s, _ = env_render.reset()
done = False
score = 0.0
while not done:
s_tensor = torch.from_numpy(s).float()
with torch.no_grad():
mu.eval() # Set the network to evaluation mode
a = mu(s_tensor).item() # Get action from the policy network
s_prime, r, done, truncated, info = env_render.step([a]) # Take action
score += r
s = s_prime
# Rendering is handled automatically with render_mode='human'
# Optional: Add a small delay for better visualization
time.sleep(0.02)
print(f"Test Episode {ep+1}: Score = {score:.1f}")
# 대기
time.sleep(1.0)
# 테스트 환경 종료
env_render.close()
if __name__ == '__main__':
main()
다른 부분들은 Actor Critic이나 DQN과 동일하기 때문에 Gauissian Noise를 더하는 부분만 살펴봅니다.
for n_epi in range(3000):
s, _ = env.reset()
done = False
count = 0
while count < 200 and not done:
a = mu(torch.from_numpy(s).float())
a = a.item() + ou_noise()[0]
s_prime, r, done, truncated, info = env.step([a])
memory.put((s,a,r/100.0,s_prime,done))
score +=r
s = s_prime
count += 1
a = a.item() + ou_noise()[0]라고 되어있는 부분이 행동에 노이즈를 더하는 역할을 수행합니다. ou_noise란 오르네스트-울렌베크 노이즈를 의미하는데, 수식에서 $N_t$라고 표현되어있는 부분을 구현하기 위해서 사용됩니다.
class OrnsteinUhlenbeckNoise:
def __init__(self, mu):
self.theta, self.dt, self.sigma = 0.1, 0.01, 0.1
self.mu = mu
self.x_prev = np.zeros_like(self.mu)
def __call__(self):
x = self.x_prev + self.theta * (self.mu - self.x_prev) * self.dt + \
self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape)
self.x_prev = x
return x
코드가 조금 복잡하지만, 현재 반환되는 노이즈인 x가 self.x_prev = x에 저장되어 다음 노이즈 생성시에 영향을 미치게 하는 것을 확인할 수 있습니다. 오르네스트-울렌베크 노이즈에 대한 좀 더 자세한 내용은 아래 링크를 참조하세요.
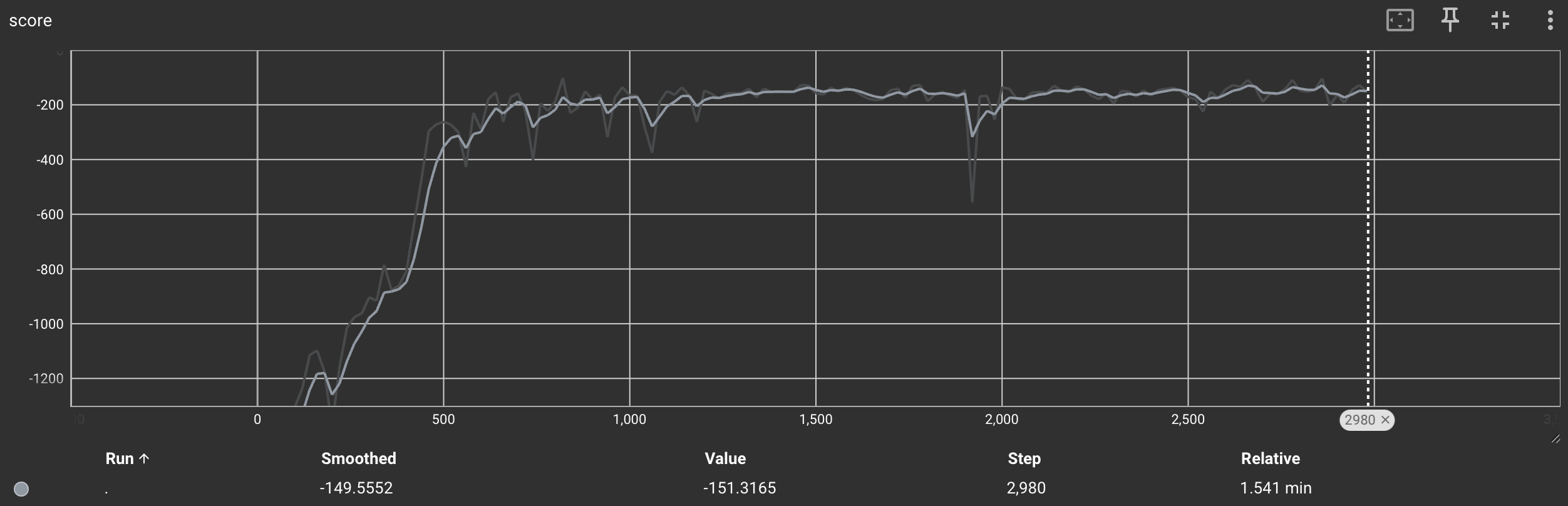
위 그림은 Pendulum-V1에서 DDPG을 학습시킨 결과입니다. 1000 Iteration 이후로는 적당한 지점에서 수렴해 더 이상 성능이 변하지 않는 것을 확인할 수 있습니다. 아래는 테스트 렌더링 결과입니다.
댓글남기기