강화학습 08: 표에 기반한 방법을 이용한 계획 및 학습
글에 들어가기 앞서…
이 포스팅은 ‘강화학습‘에 대한 내용을 담고 있습니다.
자료 출처: 단단한 강화학습, Reinforcement Learning An Introduction , 2nd edition. 리처드 서튼, 앤드류 바트로, 김성우(옮긴이)
표에 기반한 방법을 이용한 계획 및 학습
이전까지는 모델을 사용하지 않는 강화학습 방법론들에 대해서 살펴봤다면, 모델을 사용하는 방법론에 대해서 살펴봅니다. 모델은 주어져 있는 상황일 수도 있지만, 사실 모델이 주어지는 상황이 많지는 않습니다. 그런 경우에는 강화학습 에이전트가 모델을 만들어가면서 학습에 사용하게 됩니다. 그 구체적인 방법들에 대해서 살펴봅니다.
모델과 계획
블랙잭이라는 게임을 예시로 들어보면, 사실 이 게임을 파이썬으로 구현하는 것은 그렇게 어려운 일은 아닐 것 같습니다. 규칙도 굉장히 간단하면서도 승리 조건에 어떠한 모호성도 존재하지 않습니다. 게다가 에피소드 자체도 굉장히 짧게 끝납니다. 규칙이 구현되었다면, 에피소드를 뽑아내는 것은 일도 아닙니다. 그런데, 각 상태에서 다른 상태로 이동할 확률, 그 각각의 전이에서 받게될 보상들을 제공하는 표를 생성하는 일은 보다 훨씬 더 복잡한 일입니다. 그럼에도 해당 표가 주어진다면, 우리는 환경에 대해 정확하게 알 수 있게 됩니다.
이처럼 환경이 어떻게 반응할 것인지를 예측하기 위해 학습자가 사용할 수 있는 모든 것을 모델(Model)이라고 합니다. 그리고 블랙잭의 예시에서 단순히 규칙만을 구현하고 에피소드를 뽑아내는, 다시말해, 모든 가능성 중에서 확률에 따라 추출된 하나의 가능성만을 제공하는 모델을 표본 모델(Sample Model)이라고 부릅니다. 모든 가능성을 제공하고 각 가능성에 해당하는 확률을 제공하는 모델은 분포 모델(Distribution Model)이라고 불립니다. 분포 모델은 블랙잭 예시에서 모든 전이에 대한 확률 표가 주어지는 경우에 해당됩니다.
관련된 용어들이 있습니다. 표본 모델을 사용할 때에는 환경을 시뮬레이션하기 위해 모델을 사용한다고 말하고, 분포 모델을 사용할 때에는 시뮬레이션된 경험(Simulated Experience)을 만들기 위해 사용한다고 말해집니다. 그리고 이렇게 주어진 모델을 통해 가치 함수, 또는 정책을 갱신하는 작업을 통틀어 계획(Planning)이라고 말합니다.

위의 알고리즘은 무작위 표본 단일 단계 표 기반 Q 계획(Random-Sample One-Step Tabular Q-Planning)입니다. 알고리즘에 나타난 수식을 보면 알 수 있는 점인데요, 사실 Q 학습과 완전히 동일한 수식입니다. 이 알고리즘이 Q 계획이라고 불리는 이유는 다음 상태와 보상을 모델로부터 가져왔고, 이걸 사용해서 가치함수를 갱신했기 때문입니다.
다이나: 계획, 행동, 학습의 통합
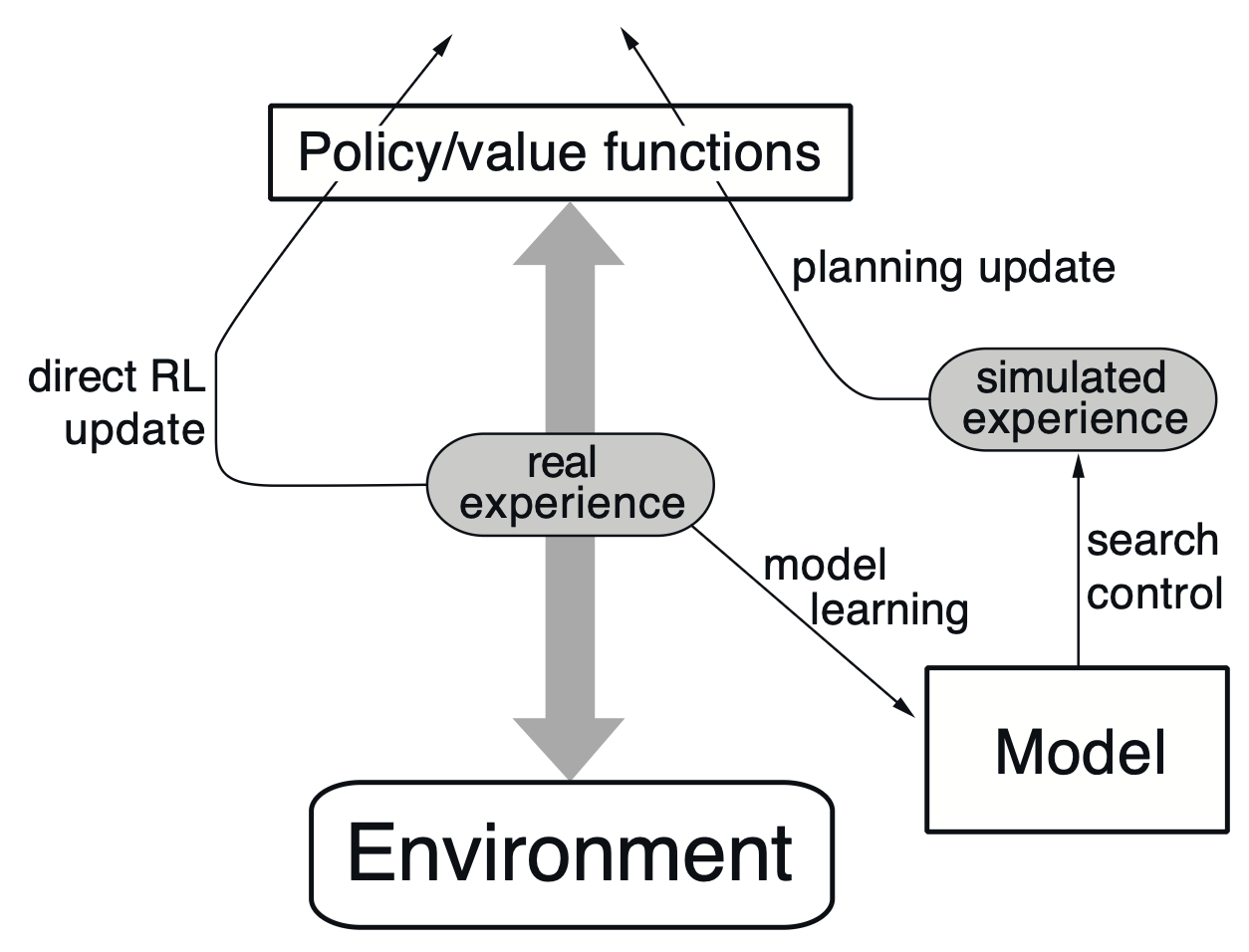
위 그림은 다이나 Q(Dyna-Q)의 구조입니다. 다이나란 계획과 행동 학습의 통합 과정을 의미합니다. 대부분의 상황에서는 모델이 주어지는 것이 아니라, 에이전트가 모델을 직접 써내려갑니다. 그리고 그 모델을 사용해서 계획을 수행합니다. 동시에 에이전트가 모델을 써내려갈 때 사용한 경험을 사용해서 학습을 수행할 수 있는데요, 이 전부를 수행하는 일련의 과정을 다이나라고 부릅니다.
관련된 용어가 있는데요, 모델로부터 계획하는 과정을 모델 학습(Model-Learning) 또는 간접적 강화학습(Indirect Reinforcement Learning)이라고 부릅니다. 그리고 경험으로부터 직접 가치 함수와 정책을 갱신하는 과정을 직접적 강화학습(Direct Reinforcement Learning)이라고 부릅니다.

계획을 사용하는 학습자는 대게 계획을 사용하지 않는 학습자에 비해 훨씬 더 빠르게 해결책을 발견합니다.
모델이 틀렸을 때
학습자가 모델을 형성할 때, 운이 좋지 않는 경우에는 편향된 데이터로 인해 잘못된 모델을 만들 수 있습니다. 이런 경우 학습자는 계획 과정에서 준최적 정책을 계산할 가능성이 높습니다. 물론 운이 좋다면 그런 경우는 발생하지는 않겠지만, 항상 운이 좋기만을 기대할 수는 없습니다.
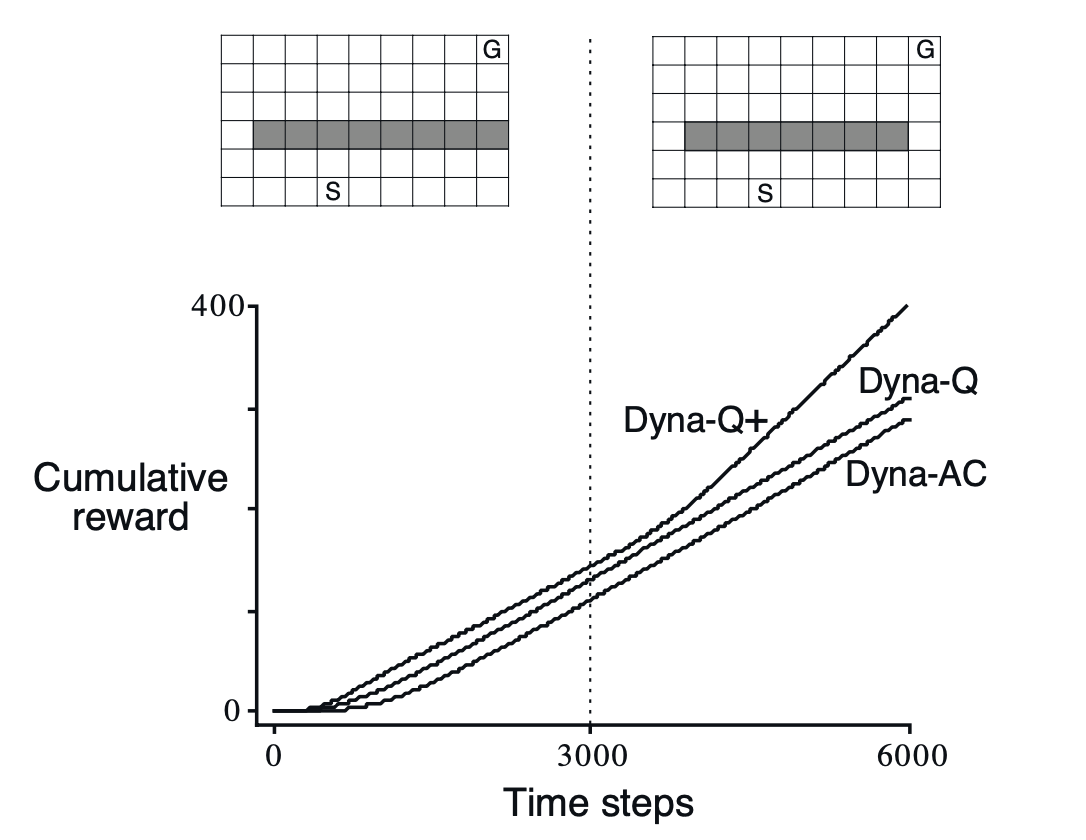
위는 다이나 Q가 변화된 환경에 적응하지 못한 예시들 중 하나입니다. 원래는 지름길이 존재하지 않고 오직 돌아가는 길만 존재했던 환경이었는데, 3000번째의 시간 단계를 기점으로 지름길이 만들어진 경우입니다. 이건 탐험과 활용 사이의 갈등에 대한 또 다른 버전이기도 한데요, 보통의 다이나 Q 학습자는 지름길이 존재한다는 사실을 절대 찾지 못합니다. 왜냐하면 이미 모델에는 지름길이 존재하지 않는다고 적혀있는 상태이고, 그에 따른 계획으로 인해 학습자가 지름길을 발견한 가능성은 매우 낮아진 상태입니다. 물론 입실론 탐욕적 정책으로 지름길을 찾을 가능성이 존재하기는 하지만, 그 확률은 매우 낮은 수준일 것입니다.
이러한 문제점을 해결하기 위해 다이나 Q+ 알고리즘이 사용되는데요, 이 알고리즘에서는 마지막으로 시도된 때로부터 얼마나 많은 시간 단계가 경과했는지에 따라 해당 상태-행동이 가지는 보상을 점차적으로 증가시킵니다(상수 $\mathcal{k}$에 대해 전이가 $\tau$만큼 시도되지 않은 경우, $\mathcal{k}\sqrt{\tau}$ 만큼의 추가 보상을 부여). 이를 통해 학습자로 하여금 접근 가능한 모든 상태 전이에 대해 계속 테스트하도록 유도합니다.
우선순위가 있는 일괄처리
다이나 Q 알고리즘을 보면, 계획 과정에서 이전에 경험했던 상태-행동에 대해서 무작위로 선택해 가치 함수의 갱신을 수행했습니다. 하지만 이러한 방법이 최선이라고 보기는 어렵습니다. 상태의 개수가 무수히 많은 경우에 초점 없는 탐색은 극도로 비효율적인 방법입니다.
대신에 가치 함수에 무언가 변화가 생긴 어떤 상태로부터든 역방향으로 진행되는것이 보다 효율적인 방법일 것입니다. 구체적으로는 특정 행동 상태의 가치가 변경되었다면, 해당 상태로 도달하도록 하는 행동의 가치를 갱신합니다. 이런 일반적인 개념을 계획 계산의 역행 초점(Backward Focusing of Planning Computation)이라고 합니다.
더 나아가서는 시급성에 따라 갱신의 우선순위를 정하고 그 우선순위에 따라 갱신을 수행하는 방법을 생각할 수 있는데요, 이를 우선순위가 있는 일괄처리(Prioritized Sweeping)라고 합니다.

우선순위가 있는 일괄처리에서 우선순위는 가치 추정값의 변화량에 따라 결정됩니다. 우선순위 큐에 담긴 상태-행동 쌍에 대해서 계획을 수행할 때, 해당 상태로 도달할 것으로 예측되는 모든 상태-행동에 대해서 가치를 추정값의 변화량을 측정하고 마찬가지로 임계값을 초과하는 경우 우선순위 큐에 추가합니다.
우선순위가 있는 일괄처리의 한계 중 하나는 기댓값 갱신을 사용한다는 점입니다. 여기에서의 기댓값 갱신은 Full-Backup으로 가능한 모든 경우를 살펴봐야 함을 의미합니다. 확률론적 환경에서는 계획 과정에서는 발생 확률이 낮은 전이에 대해 많은 계산량을 낭비할 수 있습니다.
기댓값 갱신 vs 표본 갱신
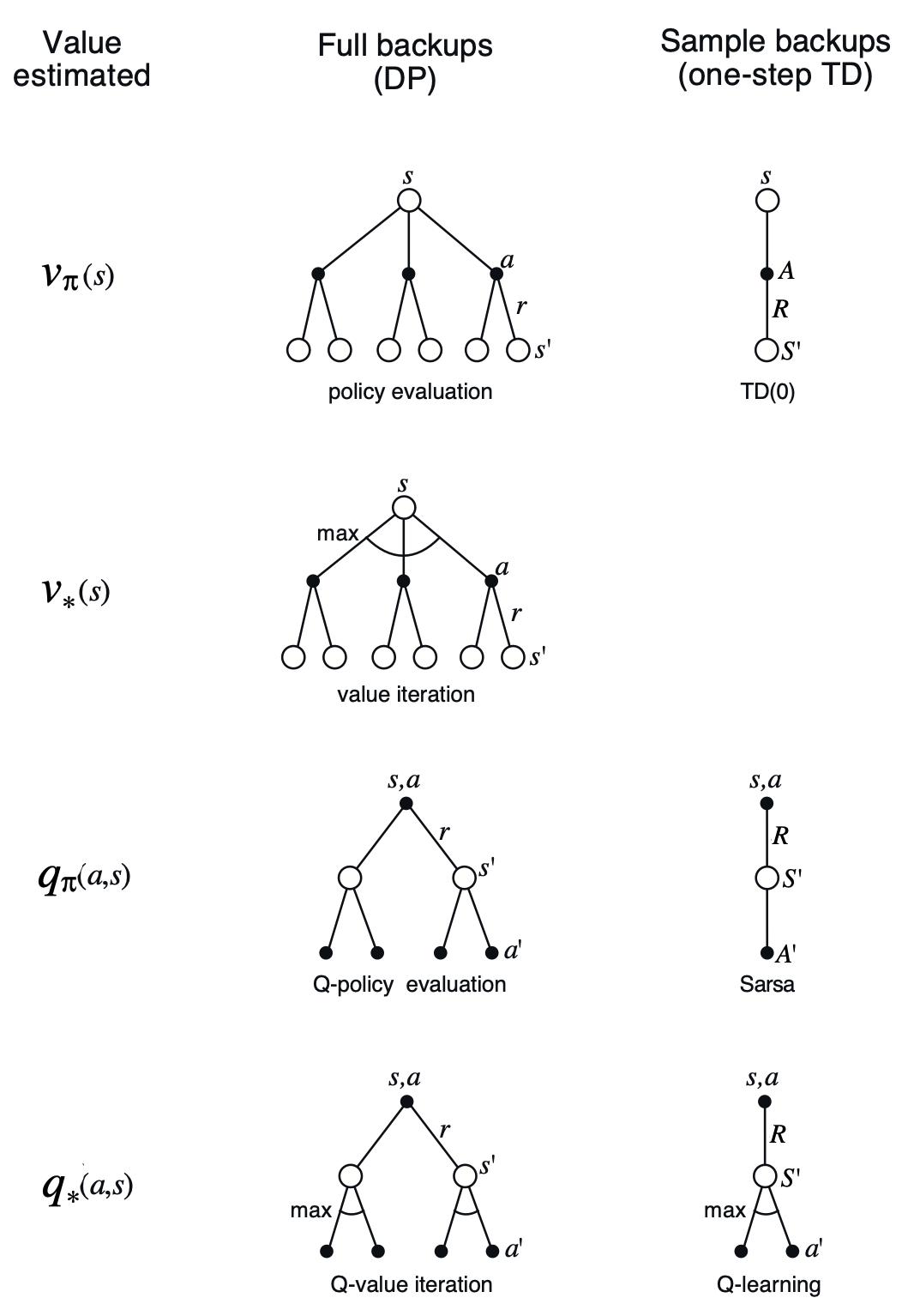
모델을 사용하는 갱신 방법에는 기댓값 갱신(Full Backup)과 표본 갱신(Sample Backup)이 있습니다. 표본 갱신을 마치 Q 학습과 같은 방식으로 이루어지는데요, 여기에서 주의해야하는 점은 Q 학습과 동일한 식을 사용할 뿐, 학습 대상 표본이 실제 환경으로부터 얻어진 샘플이 아니라 표본 모델로부터 얻어진 샘플을 사용한다는 점에서 다르다는 사실입니다.
그렇다면 기댓값 갱신과 표본 갱신이 모두 가능하면, 기댓값 갱신이 무조건 더 좋은 것일까요? 최종 결과만 따지면 그렇습니다. 하지만, 기댓값 갱신이 무조건적으로 선호되지는 않습니다. 기댓값 갱신은 계산 과정에 많은 시간을 소요하기 때문에, 시간이 충분치 않은 경우 표본 갱신이 더 적합합니다.
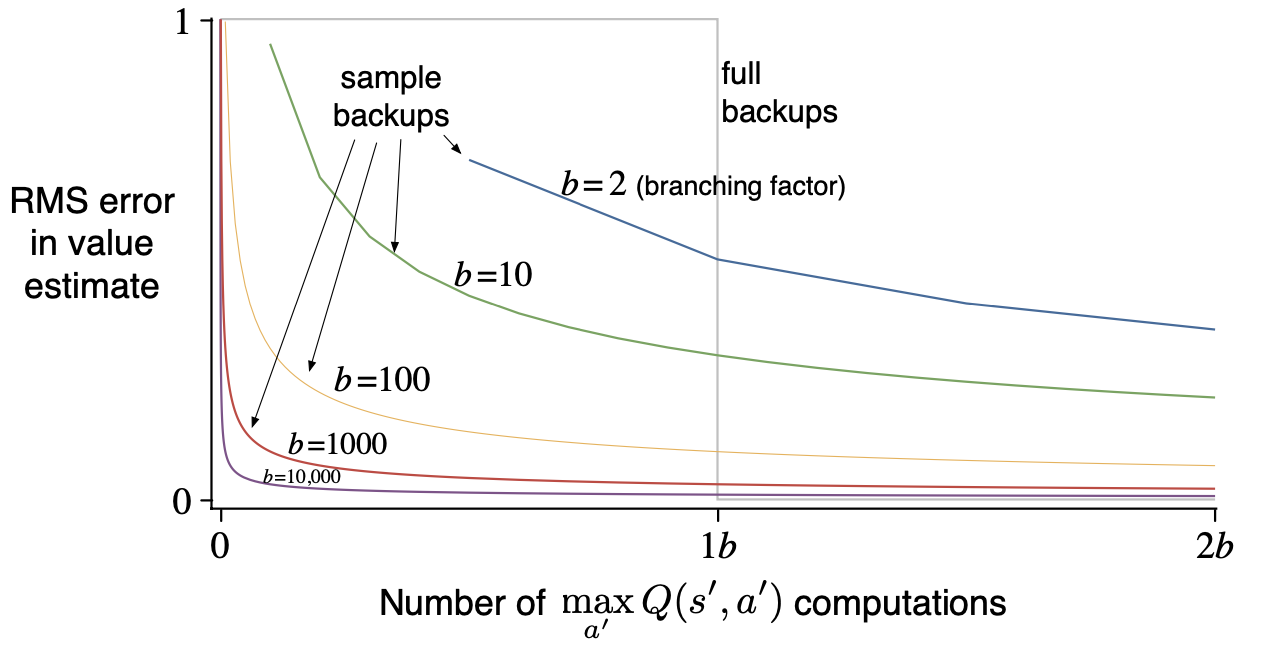
위의 그래프에서 기댓값 갱신과 표본 갱신의 성능을 비교합니다. $b$는 분기 계수(Branching Factor)로 특별한 시작 상태-행동 쌍으로 인해 도달 가능한 다음 상태의 개수를 의미합니다. 즉, 기댓값 갱신에서는 표본 갱신의 $b$배만큼의 계산량이 필요합니다. 기댓값 갱신의 그래프가 계단 형태로 나타났는데요, 기댓값 갱신은 갱신이 완료되면 추정 오차를 0으로 감소시킵니다. 반면, 표본 갱신에서는 추정오차를 $\sqrt{\frac{b-1}{bt}}$($t$는 표본 갱신의 개수)만큼씩 점진적으로 감소시킵니다. $b$가 적당히 큰 값일때, 표본 갱신의 수행 초기에 오류가 급격하게 감소하는 것을 확인할 수 있습니다. 이런 사실들을 볼 때, 갱신을 수행할 시간이 충분하지 않은 경우 표본 갱신 방법이 보다 강력한 성능을 보여줄 것입니다.
궤적 표본추출
우리가 살펴 본 모델 기반 방법들은 모델을 각 상태들의 가치 함수를 갱신할 수 있었습니다. 여기에서는 강화학습 문제를 구성하는 상태 공간에서 어떤 상태들을 갱신해야할 것인지를 다룹니다. 다이나 Q와 다이나 Q+에서 임계값을 설정하는 방법도 있었고, 우선순위과 있는 일괄처리 방법에서 어떤 순서로 상태들을 업데이트해 나가야하는지를 다루긴 했지만, 이 방법들은 다소 무작위적인 일괄적 처리 방법들입니다. 이런 철저한(Exhaustive) 일괄처리는 종종 사용되긴 하지만, 상태 공간이 넓어지는 경우에 적용하기가 매우 어렵다는 분명한 단점이 존재합니다.
또 다른 방법은 특정 분포에 따라 표본을 추출하는 것입니다. 구체적으로는 활성 정책 분포에 따라, 다시 말해 현재 정책을 따르는 동안 관측한 분포에 따라 갱신을 수행할 수 있습니다. 현재 정책과 모델과의 상호작용을 통해 표본을 바로 구할 수 있다는 장점이 존재합니다. 이러한 경험 생성 방슥을 궤적 표본추출(Trajectory Sampling)이라고 합니다.
생각해보면, 존재할 수 있는 모든 상태에 대해 갱신할 필요는 없습니다. 예를 들어 바둑을 공부할 때에도, 실제로 바둑 경기를 할 때 관측하기 어려운 상태에 대한 평가를 공부할 필요는 없을 것 같습니다. 이처럼 활성 정책 분포에 초점을 맞추면 ,흥미롭지 않은 영역을 무시하게 해 주므로 이득이 됩니다.
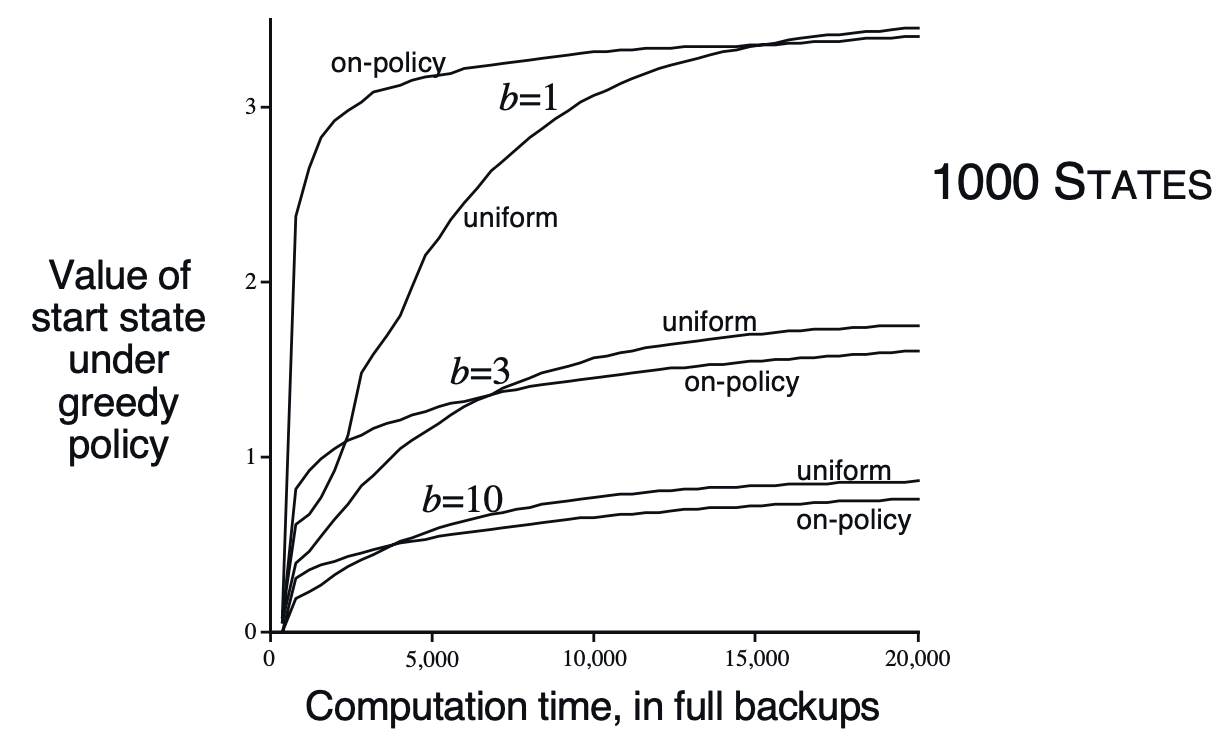
위는 간단한 실험 결과입니다. 시작 상태가 존재하고, 각 분기 계수를 가지는 환경에서 갱신 횟수에 따라 출발 상태의 가치가 어떻게 평가되는지에 대한 그래프입니다. 분기 계수가 적은 경우에 활성 정책 분포에 따른 갱신의 이점이 더 크게, 오랫동안 유지됩니다. 이는 활성 정책이 전체 상태 공간에서 차지하는 비율이 높기 때문인 것으로 해석됩니다. 장기적으로는 균일 분포에서 가치를 더 높게 평가하는데요, 이는 균일 분포에서는 활성 정책에 포함되지 않은 상태들도 갱신되었기 때문입니다.
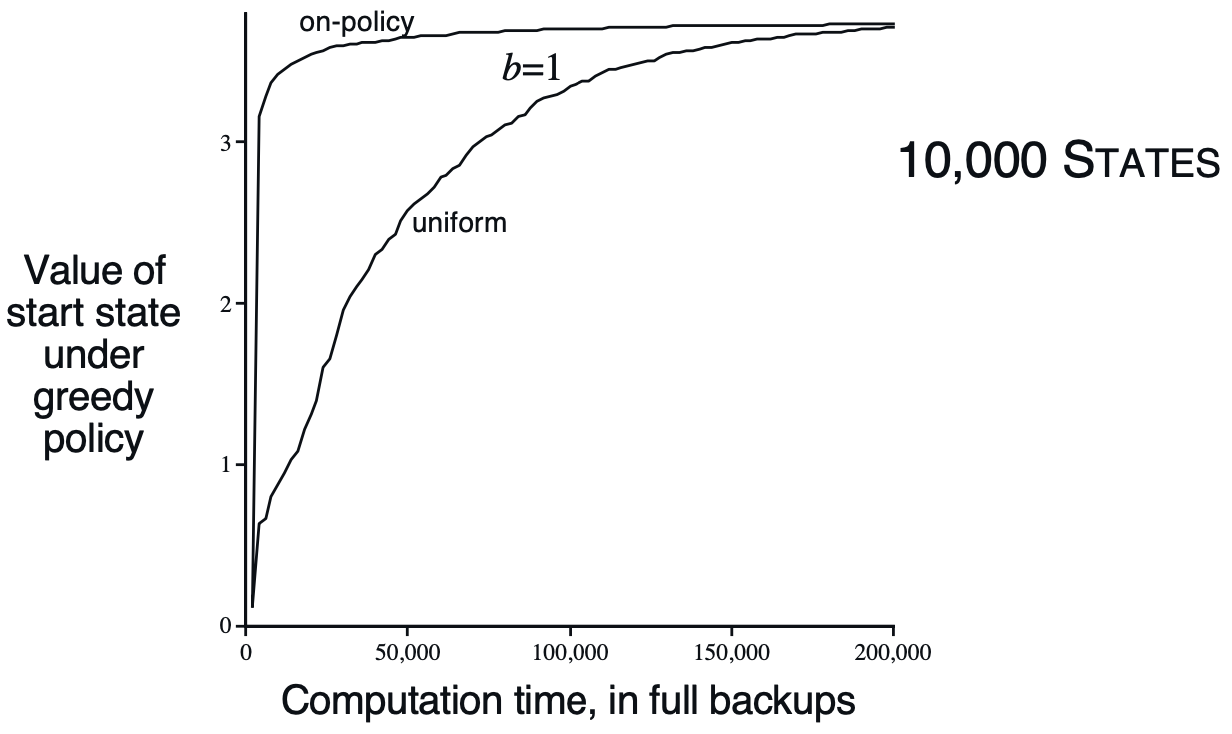
또, 상태의 개수가 많은 경우에 활성 정책 분포 평가의 이점이 더 오랫동안 유지되었는데요, 이는 흥미롭지 않은 상태들을 무시하고 중요한 상태에만 집중한 효과가 크게 나타난 것으로 해석됩니다.
실시간 동적 프로그래밍
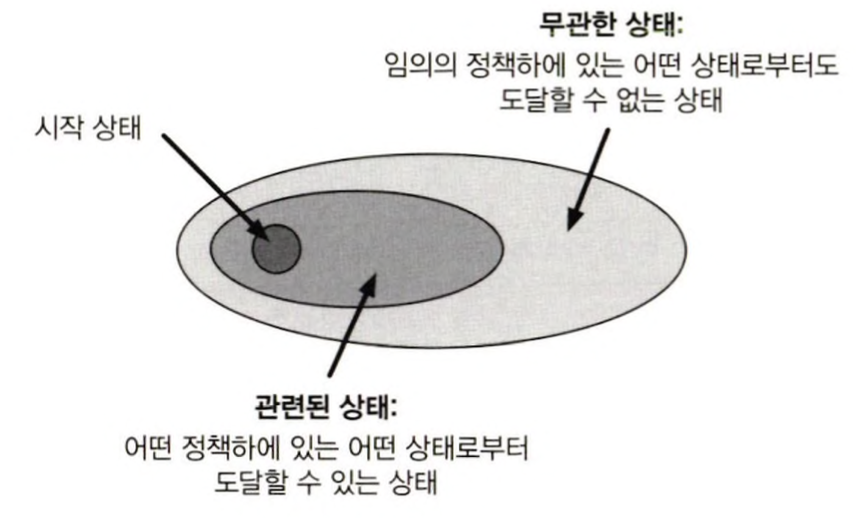
실시간 동적 프로그래밍(Real-Time Dynamic Programming, RTDP)는 가치 반복 알고리즘의 활성 정책 궤적 표본추출 버전입니다. 동적 프로그래밍에서는 모든 상태에 대해 일괄적으로 업데이트를 수행했습니다. 근데, 특정 정책이 정해져있을 때, 어떤 시작 상태로부터도 도달할 수 있는 상태가 있을 것입니다. 그리고 이 상태에 대해서는 가치 함수를 갱신할 필요도, 최적 행동을 결정할 필요도 없을 것입니다. 즉 여기서 필요한 것은 관련이 있는 상태들에 대해 최적이지만, 임의로 행동을 지정할 수 있는, 또는 무관한 정책에 대해서는 정의도차 되지 않은 최적 부분 정책(Optimal Partial Policy)입니다.
결정 시점에서의 계획
계획의 방법에 대해 살펴봤다면, 계획이 발생하는 시점에 따라서도 구분될 수 있습니다. 만약에 계획이 행동이 선택되기 한참 이전에 수행되었다면, 계획은 가치 함수 추정값 표를 갱신하는데에 사용은 되었겠지만, 지금 당장 행동을 선택하는 것에 있어 직접적인 영향을 끼치지는 않습니다. 이런 방식의 계획을 백그라운드 계획(BackGround Planning)이라고 합니다. 또 다른 방법은 현재 상태 $S_t$에 도달하고 나서 행동을 선택하기 이전에 계획을 시작하고 완료한 후, 행동을 선택하는 방식입니다. 이 방식에서는 계획이 특정 상태의 행동 선택에 직접적인 영향을 주고, 이를 결정 시간 계획(Decision-Time Planning)이라고 합니다.
경험적 탐색
여기에서 다룰 내용은 가치 함수를 어떻게 향상시킬 것인지(계획, 학습)에 대한 것이 아닙니다. 여기에서 관심이 있는 것은 이미 가치 함수가 주어진 상황에서 어떻게 정책을 선택할 것인지에 대한 내용입니다. 이를 경험적 탐색(Heuristic Search)이라고 부르는데요, 경험적 탐색에서는 다음 상태를 내다보고 트리를 만들어 가능한 행동들에 대한 보강된 가치를 계산합니다. 사실 이런 접근 방법이 이전에 종종 사용된 것 같지만, 이 개념이 가지는 차이점이 있는데요, 그것은 바로 보강된 가치를 저장하려 하지 않는다는 점입니다. 즉, 가치 함수를 업데이트를 하기 위해 보강된 가치를 계산하는 것이 아니라, 그저 다음 행동을 선택하기 위해 보강된 가치를 계산하고 행동을 선택한 이후에는 그것들을 폐기합니다. 따라서 어떻게 보면 탐욕적 정책의 개념이 단일 단계 넘어로 확장된 것이라고 해석될 수 있겠습니다.
당연히 더 깊게 탐색하기 때문에 더 좋은 행동을 선택할 수 있는데요, 완벽한 모델이 주어져 있는 상황에 불완전한 행동 가치 함수가 주어져 있다면, 더 깊게 탐색할수록 더 좋은 정책을 선택할 것입니다. 극단적으로 생각해보면, 에피소드가 끝날 때까지 탐색을 한다면 가치 함수의 효과가 완전히 사라지기 때문에, 탐색 깊이가 커질수록 더 좋은 정책이 되어간다는 주장은 대체로 사실입니다.
다시 말하면, 우리에게 어떤 가치함수가 있을 때 모든 상태에 대한 모든 정책을 구할 수도 있겠지만, 그렇게 하지 않고 지금 당장 당면한 상태에 대해서 행동을 바로바로 선택하는 방식입니다.
주사위 던지기 알고리즘
주사위 던지기(Rollout) 알고리즘은 현재 환경 상태에서 시뮬레이션된 궤적들에 적용된 몬테카를로 제어에 기반한 결정 시각 계획 알고리즘입니다. 시뮬레이션된 궤적을 생성하는 정책을 주사위 던지기 정책이라고 부르는데요, 이 정책들로 여러 궤적들을 생성하면 그들을 통해 행동 가치 추정값을 계산할 수 있을 것입니다. 행동 가치 추정값이 충분히 정확하다고 생각되면, 가장 큰 가치 기댓값을 갖는 행동이 실행됩니다.
이 과정은 정책 향상과 굉장히 구조가 비슷하다고 느껴지는데요, 행동 가치 추정값이 정확하다면, 주사위 던지기 알고리즘을 통해 결정되는 일련의 선택들(정책)은 주사위 던지기 정책보다 더 좋을 것입니다. 다시 말해, 주사위 던지기 알고리즘의 목적은 주사위 던지기 정책을 향상시킵니다.
몬테카를로 트리 탐색
몬테카를로 트리 탐색(Monte Carlo Tree Search, MCTS) 기본적으로 주사위 던지기 알고리즘과 굉장히 유사하게 동작하지만, 더욱 큰 보상을 주는 궤적을 향하게 하는 연속적인 방향 설정을 위해 몬테카를로 시뮬레이션으로 부터 얻은 가치 추정값을 축적하는 수단을 추가한다는 점에서 주사위 던지기 알고리즘보다 더욱 진보된 방식입니다.
Great Kingdom
Great Kindom은 이세돌이 만든 보드게임입니다. 이 보드게임은 바둑의 변형게임인데요, 바둑에 비해 판의 크기가 작고 규칙이 단순합니다. 이 게임을 대상으로 MCTC를 활용하는 강화학습 에이전트를 설계하겠습니다.
game.py
# game.py
import numpy as np
import sys
from collections import deque
from copy import deepcopy
EMPTY = 0
UPBOUND = 1
RIGHTBOUND = 2
DOWNBOUND = 3
LEFTBOUND = 4
NEUTRAL = 5
PLAYER1 = 6 # 파란색 성
PLAYER2 = 7 # 주황색 성
CELL_SYMBOLS = {
EMPTY: '.',
NEUTRAL: 'N',
PLAYER1: 'B',
PLAYER2: 'O',
}
TERRITORY_SYMBOLS = {
PLAYER1: '*',
PLAYER2: '+',
}
class GameState:
def __init__(self, board, current_player, consecutive_passes, game_over=False, winner=None):
self.board = board
self.current_player = current_player
self.consecutive_passes = consecutive_passes
self.game_over = game_over
self.winner = winner
class GreatKingdomGame:
def __init__(self):
self.board_size = 9
self.board = np.zeros((self.board_size, self.board_size), dtype=int)
center = self.board_size // 2
self.board[center, center] = NEUTRAL
self.current_player = PLAYER1
self.game_over = False
self.winner = None
self.consecutive_passes = 0
self.player1_territories = set()
self.player2_territories = set()
self.player1_castles = set()
self.player2_castles = set()
self.empty_indices = []
for i in range(self.board_size):
for j in range(self.board_size):
self.empty_indices.append((i, j))
self.empty_indices.remove((center, center))
def reset(self):
self.board = np.zeros((self.board_size, self.board_size), dtype=int)
center = self.board_size // 2
self.board[center, center] = NEUTRAL
self.current_player = PLAYER1
self.game_over = False
self.winner = None
self.consecutive_passes = 0
self.player1_territories.clear()
self.player2_territories.clear()
self.player1_castles.clear()
self.player2_castles.clear()
self.empty_indices = []
for i in range(self.board_size):
for j in range(self.board_size):
if (i, j) != (center, center):
self.empty_indices.append((i, j))
def search_blob_board(self, x, y, board):
if not (0 <= x < self.board_size and 0 <= y < self.board_size):
return []
if board[x, y] != EMPTY:
return []
visited = np.zeros((self.board_size, self.board_size), dtype=bool)
queue = deque()
queue.append((x, y))
blob = []
while queue:
cx, cy = queue.popleft()
if visited[cx, cy]:
continue
visited[cx, cy] = True
blob.append((cx, cy))
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = cx+dx, cy+dy
if 0 <= nx < self.board_size and 0 <= ny < self.board_size:
if board[nx, ny] == EMPTY and not visited[nx, ny]:
queue.append((nx, ny))
return blob
def compute_confirmed_territories_board(self, board):
player1_territories = set()
player2_territories = set()
empty_indices = []
for i in range(self.board_size):
for j in range(self.board_size):
if board[i, j] == EMPTY:
empty_indices.append((i, j))
while empty_indices:
indice = empty_indices[0]
blob = self.search_blob_board(*indice, board)
for x, y in blob:
empty_indices.remove((x, y))
adjacent_information = []
for x, y in blob:
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = x+dx, y+dy
if nx < 0:
adjacent_information.append(UPBOUND)
elif nx >= self.board_size:
adjacent_information.append(DOWNBOUND)
elif ny < 0:
adjacent_information.append(LEFTBOUND)
elif ny >= self.board_size:
adjacent_information.append(RIGHTBOUND)
else:
adjacent_information.append(board[nx, ny])
if (UPBOUND in adjacent_information) and (DOWNBOUND in adjacent_information) and (LEFTBOUND in adjacent_information) and (RIGHTBOUND in adjacent_information):
continue
if (PLAYER1 in adjacent_information) and (PLAYER2 in adjacent_information):
continue
if PLAYER1 in adjacent_information:
player1_territories.update(blob)
if PLAYER2 in adjacent_information:
player2_territories.update(blob)
return player1_territories, player2_territories
def place_castle(self, x, y, player=None):
if player is None:
player = self.current_player
if self.game_over:
return False
if self.board[x, y] != EMPTY:
return False
if not (0 <= x < self.board_size and 0 <= y < self.board_size):
return False
if player == PLAYER1 and (x, y) in self.player2_territories:
return False
if player == PLAYER2 and (x, y) in self.player1_territories:
return False
self.board[x, y] = player
self.empty_indices.remove((x, y))
if player == PLAYER1:
self.player1_castles.add((x, y))
else:
self.player2_castles.add((x, y))
self.seige()
self.compute_confirmed_territories()
self.consecutive_passes = 0
self.current_player = PLAYER1 if self.current_player == PLAYER2 else PLAYER2
return True
def compute_confirmed_territories(self):
# 기존 self.player1_territories, self.player2_territories 계산을 위해
self.player1_territories, self.player2_territories = self.compute_confirmed_territories_board(self.board)
def pass_turn(self):
if self.game_over:
return False
self.consecutive_passes += 1
if self.consecutive_passes >= 2:
self.game_over = True
p1_territory_count = len(self.player1_territories)
p2_territory_count = len(self.player2_territories)
if p1_territory_count >= p2_territory_count + 3:
self.winner = PLAYER1
else:
self.winner = PLAYER2
return True
self.current_player = PLAYER1 if self.current_player == PLAYER2 else PLAYER2
return True
def search_castle_blob_board(self, x, y, board):
if not (0 <= x < self.board_size and 0 <= y < self.board_size):
return []
player = board[x, y]
if player not in [PLAYER1, PLAYER2]:
return []
visited = np.zeros((self.board_size, self.board_size), dtype=bool)
queue = deque()
queue.append((x, y))
blob = []
while queue:
cx, cy = queue.popleft()
if visited[cx, cy]:
continue
visited[cx, cy] = True
blob.append((cx, cy))
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
nx, ny = cx + dx, cy + dy
if 0 <= nx < self.board_size and 0 <= ny < self.board_size:
if board[nx, ny] == player and not visited[nx, ny]:
queue.append((nx, ny))
return blob
def search_castles_board(self, board):
player1_castles = set()
player2_castles = set()
for i in range(self.board_size):
for j in range(self.board_size):
if board[i, j] == PLAYER1:
player1_castles.add((i, j))
elif board[i, j] == PLAYER2:
player2_castles.add((i, j))
return player1_castles, player2_castles
def seige_board(self, board, player):
player1_castles, player2_castles = self.search_castles_board(board)
if player == PLAYER1:
opponent_castles = list(deepcopy(player2_castles))
else:
opponent_castles = list(deepcopy(player1_castles))
game_over = False
winner = None
while not len(opponent_castles) == 0:
castle = opponent_castles[0]
blob = self.search_castle_blob_board(*castle, board)
for x, y in blob:
opponent_castles.remove((x, y))
adjacent_information = []
for x, y in blob:
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = x+dx, y+dy
if nx < 0:
adjacent_information.append(UPBOUND)
elif nx >= self.board_size:
adjacent_information.append(DOWNBOUND)
elif ny < 0:
adjacent_information.append(LEFTBOUND)
elif ny >= self.board_size:
adjacent_information.append(RIGHTBOUND)
else:
adjacent_information.append(board[nx, ny])
if player not in adjacent_information:
continue
if EMPTY in adjacent_information:
continue
game_over = True
winner = player
return game_over, winner
def get_action_size(self):
return self.board_size * self.board_size + 1
def get_valid_moves_board(self, board, player):
valid_moves = [0] * self.get_action_size()
empty_cells = []
for i in range(self.board_size):
for j in range(self.board_size):
if board[i, j] == EMPTY:
empty_cells.append((i, j))
player1_territories, player2_territories = self.compute_confirmed_territories_board(board)
if player == PLAYER1:
forbidden = player2_territories
else:
forbidden = player1_territories
for (x, y) in empty_cells:
if (x,y) not in forbidden:
valid_moves[x * self.board_size + y] = 1
valid_moves[-1] = 1
return valid_moves
def get_next_state(self, state: GameState, action):
game_over = False
winner = None
next_board = state.board.copy()
if action == self.get_action_size() - 1:
consecutive_passes = state.consecutive_passes + 1
if consecutive_passes >= 2:
# 게임 종료
temp_game = GreatKingdomGame()
temp_game.board = next_board
p1_terr, p2_terr = temp_game.compute_confirmed_territories_board(next_board)
p1_count = len(p1_terr)
p2_count = len(p2_terr)
if p1_count >= p2_count + 3:
winner = PLAYER1
else:
winner = PLAYER2
game_over = True
return GameState(next_board, state.current_player, consecutive_passes, game_over, winner)
else:
next_player = PLAYER1 if state.current_player == PLAYER2 else PLAYER2
return GameState(next_board, next_player, consecutive_passes, game_over, winner)
else:
x = action // self.board_size
y = action % self.board_size
next_board[x, y] = state.current_player
temp_game = GreatKingdomGame()
temp_game.board = next_board.copy()
game_over, winner = temp_game.seige_board(next_board, state.current_player)
if game_over:
return GameState(next_board, state.current_player, 0, game_over, winner)
else:
next_player = PLAYER1 if state.current_player == PLAYER2 else PLAYER2
return GameState(next_board, next_player, 0, game_over, winner)
def seige(self):
# 실제 게임 진행 중 place_castle 후 공성 로직
if self.current_player == PLAYER1:
opponent_castles = list(deepcopy(self.player2_castles))
else:
opponent_castles = list(deepcopy(self.player1_castles))
while not len(opponent_castles) == 0:
castle = opponent_castles[0]
blob = self.search_castle_blob(*castle)
for x, y in blob:
opponent_castles.remove((x, y))
adjacent_information = []
for x, y in blob:
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = x+dx, y+dy
if nx < 0:
adjacent_information.append(UPBOUND)
elif nx >= self.board_size:
adjacent_information.append(DOWNBOUND)
elif ny < 0:
adjacent_information.append(LEFTBOUND)
elif ny >= self.board_size:
adjacent_information.append(RIGHTBOUND)
else:
adjacent_information.append(self.board[nx, ny])
if self.current_player not in adjacent_information:
continue
if EMPTY in adjacent_information:
continue
self.game_over = True
self.winner = self.current_player
def search_castle_blob(self, x, y):
if not (0 <= x < self.board_size and 0 <= y < self.board_size):
return []
player = self.board[x, y]
if player not in [PLAYER1, PLAYER2]:
return []
visited = np.zeros((self.board_size, self.board_size), dtype=bool)
queue = deque()
queue.append((x, y))
blob = []
while queue:
cx, cy = queue.popleft()
if visited[cx, cy]:
continue
visited[cx, cy] = True
blob.append((cx, cy))
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = cx+dx, cy+dy
if 0 <= nx < self.board_size and 0 <= ny < self.board_size:
if self.board[nx, ny] == player and not visited[nx, ny]:
queue.append((nx, ny))
return blob
def print_board(self):
header = ' ' + ''.join(['{:2d}'.format(i) for i in range(self.board_size)])
print(header)
for i in range(self.board_size):
row = ' {:2d} '.format(i)
for j in range(self.board_size):
cell = self.board[i, j]
if (i, j) in self.player1_territories:
symbol = TERRITORY_SYMBOLS[PLAYER1]
elif (i, j) in self.player2_territories:
symbol = TERRITORY_SYMBOLS[PLAYER2]
else:
symbol = CELL_SYMBOLS.get(cell, '.')
row += ' ' + symbol
print(row)
print()
model.py
# model.py
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from copy import deepcopy
from game import GreatKingdomGame, GameState, PLAYER1, PLAYER2, NEUTRAL, EMPTY
import math
import random
class ResidualBlock(nn.Module):
def __init__(self, channels):
super(ResidualBlock, self).__init__()
self.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
self.bn1 = nn.BatchNorm2d(channels)
self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
self.bn2 = nn.BatchNorm2d(channels)
def forward(self, x):
residual = x
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
out += residual
out = F.relu(out)
return out
class AlphaZeroNet(nn.Module):
def __init__(self, board_size=9, num_actions=82, num_res_blocks=20, channels=256):
super(AlphaZeroNet, self).__init__()
self.board_size = board_size
self.num_actions = num_actions
self.game = GreatKingdomGame()
self.input_channels = 5
self.conv_init = nn.Conv2d(self.input_channels, channels, kernel_size=3, padding=1)
self.bn_init = nn.BatchNorm2d(channels)
self.res_blocks = nn.ModuleList([ResidualBlock(channels) for _ in range(num_res_blocks)]) ### 변경
# Policy
self.policy_conv = nn.Conv2d(channels, 2, kernel_size=1)
self.policy_bn = nn.BatchNorm2d(2)
self.policy_fc = nn.Linear(2 * board_size * board_size, num_actions)
# Value
self.value_conv = nn.Conv2d(channels, 1, kernel_size=1)
self.value_bn = nn.BatchNorm2d(1)
self.value_fc1 = nn.Linear(board_size * board_size, 256)
self.value_fc2 = nn.Linear(256, 1)
def forward(self, x):
x = F.relu(self.bn_init(self.conv_init(x)))
for block in self.res_blocks:
x = block(x)
p = F.relu(self.policy_bn(self.policy_conv(x)))
p = p.view(-1, 2 * self.board_size * self.board_size)
p = self.policy_fc(p)
p = F.log_softmax(p, dim=1)
v = F.relu(self.value_bn(self.value_conv(x)))
v = v.view(-1, self.board_size * self.board_size)
v = F.relu(self.value_fc1(v))
v = torch.tanh(self.value_fc2(v))
return p, v
def save_model(self, path='trained_alpha_zero_net.pth'):
torch.save(self.state_dict(), path)
def load_model(self, path='trained_alpha_zero_net.pth'):
self.load_state_dict(torch.load(path, map_location=torch.device('cpu')))
self.eval()
def preprocess_board(self, board):
# 5채널: PLAYER1, PLAYER2, NEUTRAL, PLAYER1_TERR, PLAYER2_TERR
p1_terr, p2_terr = self.game.compute_confirmed_territories_board(board)
board_tensor = np.zeros((5, self.game.board_size, self.game.board_size), dtype=np.float32)
for i in range(self.game.board_size):
for j in range(self.game.board_size):
cell = board[i, j]
if cell == PLAYER1:
board_tensor[0, i, j] = 1.0
elif cell == PLAYER2:
board_tensor[1, i, j] = 1.0
elif cell == NEUTRAL:
board_tensor[2, i, j] = 1.0
if (i, j) in p1_terr:
board_tensor[3, i, j] = 1.0
if (i, j) in p2_terr:
board_tensor[4, i, j] = 1.0
return torch.from_numpy(board_tensor).unsqueeze(0)
class MCTSNode:
def __init__(self, state: GameState, parent=None, parent_action=None):
self.state = state
self.parent = parent
self.parent_action = parent_action
self.children = {}
self.visits = 0
self.value = 0.0
self.untried_actions = None
def is_fully_expanded(self, valid_actions):
if self.untried_actions is None:
self.untried_actions = [a for a, valid in enumerate(valid_actions) if valid]
return len(self.untried_actions) == 0
def best_child(self, c_param=math.sqrt(2)):
choices_weights = [
(child.value / child.visits)
+ c_param * math.sqrt((2 * math.log(self.visits)) / child.visits)
for action, child in self.children.items()
]
return list(self.children.values())[np.argmax(choices_weights)]
def expand(self, action, next_state: GameState):
child_node = MCTSNode(next_state, parent=self, parent_action=action)
self.children[action] = child_node
if self.untried_actions is not None and action in self.untried_actions:
self.untried_actions.remove(action)
return child_node
def update(self, value):
self.visits += 1
self.value += value
class MCTS:
def __init__(self, game: GreatKingdomGame, network: AlphaZeroNet, iterations=1000, c_param=math.sqrt(2)):
self.game = game
self.network = network
self.iterations = iterations
self.c_param = c_param
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.network.to(self.device)
self.network.eval()
def run_mcts(self, initial_state: GameState):
root = MCTSNode(initial_state)
for _ in range(self.iterations):
node = root
state = deepcopy(initial_state)
# Selection
while not state.game_over and node.is_fully_expanded(self.game.get_valid_moves_board(state.board, state.current_player)):
node = node.best_child(self.c_param)
action = node.parent_action
state = self.game.get_next_state(state, action)
# Expansion
if not state.game_over:
valid_moves = self.game.get_valid_moves_board(state.board, state.current_player)
if node.untried_actions is None:
node.untried_actions = [a for a, valid in enumerate(valid_moves) if valid]
if node.untried_actions:
action = random.choice(node.untried_actions)
state = self.game.get_next_state(state, action)
node = node.expand(action, state)
# Evaluation
if state.game_over:
if state.winner == PLAYER1:
value = 1
elif state.winner == PLAYER2:
value = -1
else:
value = 0
else:
board_tensor = self.network.preprocess_board(state.board).to(self.device)
with torch.no_grad():
policy, value = self.network(board_tensor)
value = value.cpu().numpy()[0][0]
# Backpropagation
while node is not None:
node.update(value)
value = -value
node = node.parent
return root
def search(self, initial_state: GameState):
root = self.run_mcts(initial_state)
if not root.children:
return self.game.get_action_size() -1
actions, visits = zip(*[(action, child.visits) for action, child in root.children.items()])
best_action = actions[np.argmax(visits)]
return best_action
train_self_play.py
# train_self_play.py
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
from copy import deepcopy
from collections import deque
import random
import matplotlib.pyplot as plt
from game import GreatKingdomGame, GameState, PLAYER1, PLAYER2, NEUTRAL, EMPTY
from model import AlphaZeroNet, MCTS
import os
import time
time_now = time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(time.time()))
def preprocess_board_for_training(board, board_size=9):
temp_game = GreatKingdomGame()
temp_game.board = board.copy()
p1_terr, p2_terr = temp_game.compute_confirmed_territories_board(board)
board_tensor = np.zeros((5, board_size, board_size), dtype=np.float32)
for i in range(board_size):
for j in range(board_size):
cell = board[i, j]
if cell == PLAYER1:
board_tensor[0, i, j] = 1.0
elif cell == PLAYER2:
board_tensor[1, i, j] = 1.0
elif cell == NEUTRAL:
board_tensor[2, i, j] = 1.0
if (i, j) in p1_terr:
board_tensor[3, i, j] = 1.0
if (i, j) in p2_terr:
board_tensor[4, i, j] = 1.0
return board_tensor
def self_play_episode(game: GreatKingdomGame, network: AlphaZeroNet, mcts_iterations=100, temperature=1):
states = []
mcts_policies = []
current_players = []
moves = []
state = GameState(deepcopy(game.board), game.current_player, game.consecutive_passes, game.game_over, game.winner)
mcts = MCTS(game, network, iterations=mcts_iterations)
while not state.game_over:
board_tensor = preprocess_board_for_training(state.board, board_size=game.board_size)
valid_moves = game.get_valid_moves_board(state.board, state.current_player)
root = mcts.run_mcts(state)
visit_counts = []
for a in range(game.get_action_size()):
child = root.children.get(a)
if child is not None:
visit_counts.append(child.visits)
else:
visit_counts.append(0)
visit_counts = np.array(visit_counts, dtype=np.float32)
if temperature == 0:
best_action = np.argmax(visit_counts)
pi = np.zeros_like(visit_counts)
pi[best_action] = 1.0
else:
if visit_counts.sum() > 0:
visit_counts = visit_counts ** (1.0 / temperature)
pi = visit_counts / visit_counts.sum()
else:
pi = np.zeros_like(visit_counts)
pi[-1] = 1.0
states.append(board_tensor)
mcts_policies.append(pi)
current_players.append(state.current_player)
action = np.random.choice(len(pi), p=pi)
if action == game.get_action_size() - 1:
moves.append((state.current_player, 'pass'))
else:
x = action // game.board_size
y = action % game.board_size
moves.append((state.current_player, x, y))
next_state = game.get_next_state(state, action)
state = next_state
if state.winner == PLAYER1:
z = 1.0
elif state.winner == PLAYER2:
z = -1.0
else:
z = 0.0
training_data = []
for s, pi, p in zip(states, mcts_policies, current_players):
if p == PLAYER1:
training_data.append((s, pi, z))
else:
training_data.append((s, pi, -z))
return training_data, moves, state.winner, state
def flip_up_down(state):
return np.flipud(state)
def flip_left_right(state):
return np.fliplr(state)
def rotate_180(state):
return np.rot90(state, 2, axes=(1, 2))
def flip_pi_up_down(pi, board_size):
pass_index = board_size*board_size
pi_2d = pi[:pass_index].reshape(board_size, board_size)
pi_2d = np.flipud(pi_2d)
pi_new = pi_2d.flatten()
pi_new = np.append(pi_new, pi[pass_index])
return pi_new
def flip_pi_left_right(pi, board_size):
pass_index = board_size*board_size
pi_2d = pi[:pass_index].reshape(board_size, board_size)
pi_2d = np.fliplr(pi_2d)
pi_new = pi_2d.flatten()
pi_new = np.append(pi_new, pi[pass_index])
return pi_new
def flip_pi_180(pi, board_size):
pass_index = board_size*board_size
pi_2d = pi[:pass_index].reshape(board_size, board_size)
pi_2d = np.rot90(pi_2d, 2)
pi_new = pi_2d.flatten()
pi_new = np.append(pi_new, pi[pass_index])
return pi_new
def augment_data(states, pis, vs, board_size=9):
augmented_states = []
augmented_pis = []
augmented_vs = []
for s, pi, v in zip(states, pis, vs):
transform_type = random.choice(['ud', 'lr', '180', 'none'])
if transform_type == 'ud':
s_aug = flip_up_down(s)
pi_aug = flip_pi_up_down(pi, board_size)
elif transform_type == 'lr':
s_aug = flip_left_right(s)
pi_aug = flip_pi_left_right(pi, board_size)
elif transform_type == '180':
s_aug = rotate_180(s)
pi_aug = flip_pi_180(pi, board_size)
else:
s_aug = s
pi_aug = pi
augmented_states.append(s_aug)
augmented_pis.append(pi_aug)
augmented_vs.append(v)
return np.array(augmented_states), np.array(augmented_pis), np.array(augmented_vs)
def get_final_game_state_str(final_state: GameState):
temp_game = GreatKingdomGame()
temp_game.board = final_state.board.copy()
p1_terr, p2_terr = temp_game.compute_confirmed_territories_board(final_state.board)
CELL_SYMBOLS = {
EMPTY: '.',
NEUTRAL: 'N',
PLAYER1: 'B',
PLAYER2: 'O',
}
TERRITORY_SYMBOLS_P1 = '*'
TERRITORY_SYMBOLS_P2 = '+'
board_size = temp_game.board_size
lines = []
header = ' ' + ''.join(['{:2d}'.format(i) for i in range(board_size)])
lines.append(header)
for i in range(board_size):
row_str = ' {:2d} '.format(i)
for j in range(board_size):
cell = final_state.board[i, j]
if (i, j) in p1_terr:
symbol = TERRITORY_SYMBOLS_P1
elif (i, j) in p2_terr:
symbol = TERRITORY_SYMBOLS_P2
else:
symbol = CELL_SYMBOLS.get(cell, '.')
row_str += ' ' + symbol
lines.append(row_str)
lines.append('')
return '\n'.join(lines)
def print_final_game_state(final_state: GameState):
board_str = get_final_game_state_str(final_state)
print(board_str)
def run_training_loop(num_iterations=100,
games_per_iteration=50,
mcts_iterations=800,
batch_size=64,
epochs=10,
lr=0.001,
pretrained_model=None):
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
game = GreatKingdomGame()
if pretrained_model is not None:
print("Pretrained model loaded")
network = AlphaZeroNet(board_size=9, num_actions=82, num_res_blocks=20, channels=256)
network.load_model(pretrained_model)
network.to(device)
else:
network = AlphaZeroNet(board_size=9, num_actions=82, num_res_blocks=20, channels=256).to(device)
optimizer = optim.Adam(network.parameters(), lr=lr)
loss_fn = nn.MSELoss()
replay_buffer = deque(maxlen=50000)
total_losses = []
policy_losses = []
value_losses = []
for it in range(num_iterations):
print(f"=== Iteration {it+1}/{num_iterations} ===")
iteration_data = []
all_moves = []
final_states = []
if it < 10:
temperature = 1.0
elif it < 20:
temperature = 0.5
elif it < 50:
temperature = 0.25
elif it < 90:
temperature = 0.1
else:
temperature = 0.0
for g in range(games_per_iteration):
game.reset()
episode_data, moves, winner, final_state = self_play_episode(game, network, mcts_iterations=mcts_iterations, temperature=temperature)
iteration_data.extend(episode_data)
all_moves.append((moves, winner))
final_states.append(final_state)
replay_buffer.extend(iteration_data)
if not os.path.exists("play_note"):
os.makedirs("play_note")
if not os.path.exists(f"play_note/{time_now}"):
os.makedirs(f"play_note/{time_now}")
note_path = f"play_note/{time_now}/iteration_{it+1}_games.txt"
with open(note_path, 'w') as f:
for idx, (moves, winner) in enumerate(all_moves):
f.write(f"Game {idx+1}:\n")
for mv in moves:
if mv[1] == 'pass':
f.write(f"Player {mv[0]}: pass\n")
else:
f.write(f"Player {mv[0]}: {mv[1]}, {mv[2]}\n")
f.write(f"Winner: {winner}\n\n")
f.write("Last Game Final Board State:\n")
final_board_str = get_final_game_state_str(final_states[-1])
f.write(final_board_str)
print("Iteration 마지막 게임의 최종 보드 상태:")
print_final_game_state(final_states[-1])
rb_list = list(replay_buffer)
it_policy_loss = []
it_value_loss = []
it_total_loss = []
for e in range(epochs):
random.shuffle(rb_list)
batches = [rb_list[i:i+batch_size] for i in range(0, len(rb_list), batch_size)]
for batch in batches:
states, target_pis, target_vs = zip(*batch)
states = np.array(states, dtype=np.float32)
target_pis = np.array(target_pis, dtype=np.float32)
target_vs = np.array(target_vs, dtype=np.float32)
states, target_pis, target_vs = augment_data(states, target_pis, target_vs, board_size=9)
states = torch.tensor(states, dtype=torch.float32, device=device)
target_pis = torch.tensor(target_pis, dtype=torch.float32, device=device)
target_vs = torch.tensor(target_vs, dtype=torch.float32, device=device).unsqueeze(-1)
p, v = network(states)
policy_loss = -(target_pis * p).sum(dim=1).mean()
value_loss = loss_fn(v, target_vs)
loss = policy_loss + value_loss
optimizer.zero_grad()
loss.backward()
optimizer.step()
it_policy_loss.append(policy_loss.item())
it_value_loss.append(value_loss.item())
it_total_loss.append(loss.item())
mean_policy_loss = np.mean(it_policy_loss) if it_policy_loss else 0
mean_value_loss = np.mean(it_value_loss) if it_value_loss else 0
mean_total_loss = np.mean(it_total_loss) if it_total_loss else 0
print(f"Iteration {it+1}: Total Loss={mean_total_loss:.4f}, Policy Loss={mean_policy_loss:.4f}, Value Loss={mean_value_loss:.4f}")
if not os.path.exists("checkpoint"):
os.makedirs("checkpoint")
if not os.path.exists(f"checkpoint/{time_now}"):
os.makedirs(f"checkpoint/{time_now}")
network.save_model(f"checkpoint/{time_now}/alpha_zero_checkpoint_{it+1}.pth")
network.save_model("alpha_zero_final.pth")
print("학습 완료")
plt.figure(figsize=(10,6))
plt.plot(total_losses, label='Total Loss')
plt.plot(policy_losses, label='Policy Loss')
plt.plot(value_losses, label='Value Loss')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Training Loss over Iterations')
plt.legend()
plt.savefig('training_loss.png')
plt.show()
if __name__ == "__main__":
run_training_loop(
num_iterations=100,
games_per_iteration=50,
mcts_iterations=800,
batch_size=64,
epochs=10,
lr=0.001,
pretrained_model=None
)
위의 파이썬 파일을 통해 Great Kindom에 대해 MCTS 방법론으로 모델을 학습시킬 수 있습니다. 구체적으로는 알파고 제로의 구조를 사용했는데요, 아래의 논문에 구체적인 방법론이 소개되어 있습니다. 그리고 코드를 구현해놓은 깃허브 주소를 첨부했으니 필요시 참고 바랍니다.
댓글남기기