4 분 소요

글에 들어가기 앞서…

이 포스팅은 ‘강화학습‘에 대한 내용을 담고 있습니다.

자료 출처: 단단한 강화학습, Reinforcement Learning An Introduction , 2nd edition. 리처드 서튼, 앤드류 바트로, 김성우(옮긴이)

시간차 학습

시간차(Temporal-Difference) 학습은 강화학습에서 정말 중요한 개념 중 하나입니다. TD 학습은 동적 프로그래밍과 몬테카를로를 결합한 방법이라고도 말해지는데요, 아래의 특성 때문에 그렇습니다.

  • 몬테카를로 방식과 가팅 환경의 동역학에 대한 모델이 없이, 경험만으로부터 직접 학습을 할 수 있음
  • DP 방식에서 처럼 다른 학습된 추정값을 기반으로 추정값을 갱신하는 부트스트랩 방식을 사용함.

TD 예측

\[V(S_t) \leftarrow V(S_t) + \alpha[G_t - V(S_t)]\] \[V(S_t) \leftarrow V(S_t) + \alpha[R_{t+1} + \gamma V(S_{t+1}) - V(S_t)]\]

위의 식은 우리가 이전 포스트에서 다루었던 몬테카를로 방법의 추정값 갱신 규칙입니다. 그 아래가 바로 우리가 살펴볼 TD 예측의 갱신 규칙이 되는데요, 식을 보고 알 수 있는 사실은, 또 다른 추정값을 보고 추정값을 갱신하는 과정을 수행한다는 점입니다.

TD 예측에서 갱신의 기준이 되는 지점은 바로 다음 상태의 상태 가치 함수 값입니다. 때문에 에피소드가 끝나지 않은 상황에서도, 또는 에피소드가 절대로 끝나지 않는 그런 환경에서도 TD 예측을 사용할 수 있습니다.

생각해보면 바로 다음 상태만을 보고 갱신을 하지 않을 수도 있는데요, 이후 두 상태를 참조할 수도, 세 상태를 참조할 수도 있습니다. 그리고 실제로 그런 방법들은 유효합니다. 위의 식과 같이 오직 다음 상태만을 참조해 업데이트하는 방식을 특별히 TD(0) 또는 단일 단계(One-Step) TD라고 부릅니다.

image-20241123144716021

위는 TD(0)의 알고리즘입니다. TD도, DP도 부트스트랩을 사용하지만, 약간의 차이가 있습니다. DP에서 일어나는 갱신은 가능한 이후상태의 완전한 분포를 대상을 합니다. 반면, TD, MC(Monte-Carlo) 방식의 갱신 대상은 단일 표본을 기반으로 합니다. 이를 표본 갱신(Sample Update)이라고 합니다.

\(\delta_t \doteq R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\) 현재의 추정값과 더 좋은 추정값 사이의 차이는 일종의 오차로 이해될 수 있는데요, 이를 TD 오차(TD Error)라고 부릅니다.

Random Walk

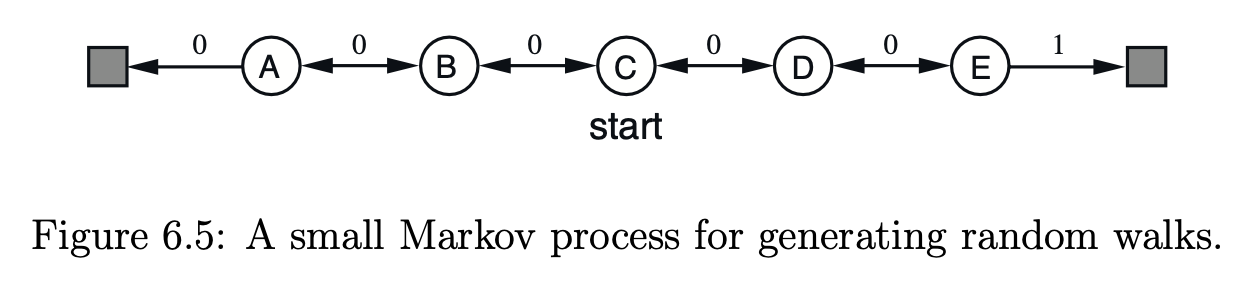
image-20241123150449013

무작위 행보 환경은 위와 같은데요, 여기에서 에이전트는 무작위로 오른쪽, 또는 왼쪽으로 이동합니다. 이 경우에 각 상태가 가지는 가치함수를 TD(0) 방법으로 구하는 파이썬 코드는 아래와 같습니다.

import numpy as np

states = ['Terminal', 'A', 'B', 'C', 'D', 'E', 'Terminal']
state_indices = {state: idx for idx, state in enumerate(states)}

V = np.zeros(len(states))
V[state_indices['Terminal']] = 0.0

alpha = 0.1
gamma = 1.0
num_episodes = 1000
start_state = 'C'

for episode in range(num_episodes):
    state = start_state

    while state != 'Terminal':
        state_idx = state_indices[state]
        action = np.random.choice([-1, 1])
        next_state_idx = state_idx + action
        next_state = states[next_state_idx]

        if next_state == 'Terminal' and next_state_idx == len(states) - 1:
            reward = 1
        else:
            reward = 0

        V[state_idx] += alpha * (reward + gamma * V[next_state_idx] - V[state_idx])
        state = next_state


for state in states[1:-1]:
    print(f"상태 {state}의 가치 추정값: {V[state_indices[state]]:.4f}")

TD와 MC의 차이

image-20241123154825274

위와 같은 샘플들이 주어졌을 때, 각 상태의 가치 함수는 어떻게 될까요? 상태 $B$의 가치 함수 값이 $\frac{3}{4}$이 되어야 한다는 것은 모두가 인정할 수 있는 사실입니다. 문제는 $A$입니다.

우리에게 주어진 데이터셋을 살펴보면, $A$에서는 오직 0의 이득만을 가졌습니다. 때문에, $V(A) = 0$ 이라고 추정할 수 있습니다. 또 다른 합리적인 답변은, 상태 $A$는 항상 상태 $B$로 전이되었기 때문에, $V(A) = \frac{3}{4}$ 가 되어야 한다는 주장입니다.

첫 번째 주장은 일괄 몬테카를로 방법이 주는 답변이고, 두 번째 주장은 일괄 TD(0) 방식이 주는 답변입니다. 훈련 데이터만을 살펴보면 몬테카를로 방식이 더 좋은 결과를 도출합니다만, 두 번때 답변이 미래의 데이터에 대해서는 더 작은 오차를 낼 것으로 기대됩니다. 이는 일괄 TD(0)가 마르코프 과정의 최대 공산(Maximum-Likelihood) 모델에 대한 올바른 추정값을 찾기 때문입니다.

SARSA

TD에서도 마찬가지로 상태 가치 함수를 학습하는 것 보단 상태-행동 가치 함수를 학습하는 것이 실용적입니다.

\(Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)]\) 위 식에서 사용되는 사건은 $(S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1})$ 이렇게 총 5개인데요, 이런 이유로 알고리즘의 이름이 SARSA가 되었습니다.

image-20241123160830536

Q 학습

\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma \space \underset{a}max\space Q(S_{t+1}, a) - Q(S_t, A_t)]\]

image-20241123161431899

Q 학습(Q-learning)에서는 학습 대상이 자신의 행동이 아닌, 그 당시에 선택할 수 있었던 최대의 가치를 가지는 행동입니다. 이는 마치 에이전트가 실제로 경험하지 않은 행동을 대상으로 학습하는 것과 동일한데요, 때문에 Q 학습은 비활성 정책 TD 제어 방법중 하나입니다.

기댓값 살사

\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma \mathbb{E}_\pi [Q(S_{t+1}, A_{t+1})|S_{t+1}] - Q(S_t, A_t)]\] \[\leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma \sum_a \pi(a|S_{t+1}) Q(S_{t+1}, a) - Q(S_t, A_t)]\]

위는 기댓값 살사의 갱신 규칙입니다. 이 알고리즘은 살사가 기댓값을 기준으로 이동하는 방향과 동일한 방향으로 결정론적으로 이동하기 때문에 기댓값 살사(Expected SARSA)라고 불리웁니다.

기댓값 살사는 살사보다 계산은 더 복잡하지만, 무작위 선택으로 인한 분산을 없애줍니다. 때문에 동일한 양의 경험이 주어지면 일반적으로 기댓값 살사가 살사보다 더 좋은 성능을 보여줍니다. 위의 식에서는 에이전트의 정책 $\pi$가 사용되었지만, 일반적으로는 다른 정책을 사용하게 되고, 이 경우에는 비활성 정책 알고리즘이 됩니다.

최대화 편차

지금까지 논의한 모든 제어 알고리즘은 최대화 과정을 포함합니다. Q 학습에서는 갱신 규칙 자체에서 최대값을 사용하고, 입실론 탐욕적 정책을 사용하는 것 역시 최대화 과정을 포함합니다. 이렇게 가치 추정값의 최댓값을 최대 가치의 추정 값으로 사용하는 것은 상당한 양의 편차를 만들어낼 수 있습니다. 예를 들어 특정 상태 $s$의 모든 행동들의 실제 가치가 0인 상황을 생각해 보겠습니다. 실제로는 값이 0이지만, 그 가치의 추정값은 불확실성으로 인해, 일부는 양수이고 일부는 음수일 수 있습니다. 이때 해당 상태의 추정값의 최댓값은 양수가 됩니다. 때문에 양의 편차가 발생하고 이를 최대화 편차(Maximization Bias)라고 합니다.

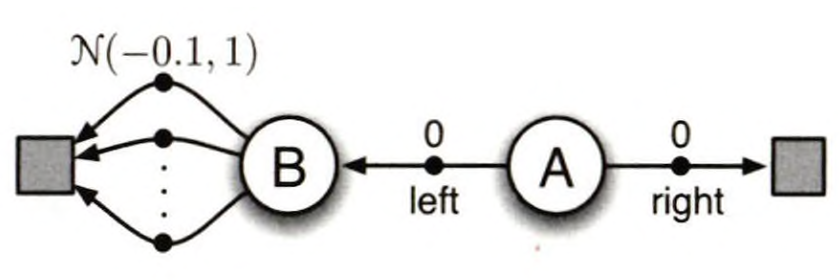
image-20241123164257525

위와 같은 환경이 있다면, 왼쪽으로 움직이는 행동을 선택했다면 명백하게 실수입니다. 그럼에도 실제로 Q 학습을 시켜보면, 초기에 왼쪽을 강하게 선호하는 현상이 나타납니다. 심지어는 에피소드를 많이 수행한 이후에도 최적보다 더 자주 왼쪽 행동을 선호합니다.

\[Q_1(S_t, A_t) \leftarrow Q_1(S_t, A_t) + \alpha[R_{t+1} + \gamma Q_2(S_{t+1}, \underset{a}{argmax}\space Q_1(S_{t+1}, a)) - Q_1(S_t, A_t)]\]

이중 Q 학습(Double Q-Learning)은 최대화 편차를 효과적으로 줄여줍니다. 최대화 편차를 발생시키는 큰 요인 중 하나는 동일한 데이터로 학습된 가치 함수를 행동을 선택할 때에도 사용하고, 행동을 평가할 때에도 사용하는 점입니다. 위와 같이 평균이 $-0.1$인 정규분포를 따르는 보상을 받는다면, 일부는 양수에 해당되는 보상을 받을 수 있습니다. 물론 궤적의 개수가 무한에 다다르면 그 값은 평균값에 수렴하지만, 학습 초기 불안정한 구간에서는 일부 행동에 대해서 양수 보상이 주어진다면 해당 행동의 가치 함수값 역시 양수로 정해지게 되고, 해당 가치 함수 값을 기준으로 그 이전 행동에 대한 가치 함수의 값도 갱신됩니다. 이런 악순환에 의해서 학습 초기 좋지 않은 행동을 계속 선택할 가능성이 높습니다.

\[A^* = \underset{a}{argmax}\space Q_1(a)\] \[\mathbb{E}[Q_2(A^*)] = q(A^*)\]

이중 학습에서는 행동을 선택하는 가치 함수($Q_1$)와 행동을 평가하는 가치 함수($Q_2$)를 따로 사용합니다(0.5의 확률로 두 개의 가치 함수 자리를 번갈아가면서 사용함). 이렇게 가치 함수를 두 개를 사용하면 $Q_1$이 좋다고 평가한 행동에 대해 $Q_2$는 독립적인 데이터로 갱신되어온 값을 가지기 때문에 최대화 편차가 사라집니다.

댓글남기기

참고