강화학습 05: 몬테카를로 방법
글에 들어가기 앞서…
이 포스팅은 ‘강화학습‘에 대한 내용을 담고 있습니다.
자료 출처: 단단한 강화학습, Reinforcement Learning An Introduction , 2nd edition. 리처드 서튼, 앤드류 바트로, 김성우(옮긴이)
몬테카를로 방법
이전 장에서는 동역학이 주어져 있는 상황에서 사용할 수 있는 동적 프로그래밍 방법을 통한 가치함수 추정 방법에 대해 알아봤습니다. 하지만 동적 프로그래밍은 사실 모든 경우를 다 살펴보는 방법이기 때문에 시간 소요가 굉장히 심하다는 단점이 있습니다. 더욱이 동역학이 존재하지 않는 경우에는 동적 프로그래밍은 사용조차 할 수 없습니다. 이런 여러가지 단점들을 해결할 수 있는 방법이 있는데요, 그것은 바로 샘플 기반 가치 함수 추정 방법입니다. 샘플 기반 가치 함수 추정 방법에서는 동역학이 필요하지 않습니다. 여기에서 필요한 것은 큰 수의 법칙을 만족시킬 수 있을 만큼의 많은 샘플의 개수입니다.
몬테카를로라는 단어는 무작위성을 포함하는 추정 과정을 나타내는 넓은 의미로 사용되기도 하는데요, 강화학습에서 몬테카를로는 보다 좁은 의미로 사용됩니다. 정확하게는, 온전한 이득에 대한 평균값을 기반으로 하는 방법을 의미합니다. 2장의 다중선택에서와 다른 점은, 보상이 아닌 이득(Return)을 예측한다는 점에 있습니다.
몬테카를로 예측
몬테카를로 예측은 굉장히 단순한 아이디어입니다. 실제로 경험을 해보고, 경험으로부터의 평균값으로 상태의 가치 함수를 추정합니다. 특정 에피소드에서 지나치는 다양한 상태들이 있을텐데, 각 상태를 지나치면서 부터 받았던 보상 정보들이 모두 주어져 있고, 이것을 할인해 더하든, 온전히 더하든, 아무튼 이득을 구할 수 있습니다. 무수히 많은 에피소드가 주어진다면, 그 평균값은 참 값에 가까워 질 것입니다.
한 에피소드에서 특정 상태 $s$를 지나치는 것을 접촉(Visit)이라고 합니다. 이것은 해당 상태의 가치 함수를 추정하기 위한 데이터가 됩니다. 생각을 해보면, 하나의 에피소드에서 특정 상태를 두 번 접촉하는 것이 결코 불가능한 일은 아닙니다. 만약 이런 상황이 발생한다면, 처음 해당 상태를 접촉한 경우만 평균에 포함할 것인지, 아니면 접촉한 모든 경우들을 다 평균에 포함할 것인지에 따라 몬테카를로 예측 방법이 나뉘게 됩니다. 전자를 최초 접촉 MC 방법(First-Visit MC Method)이라고 부르고, 후자를 모든 접촉 MC 방법(Every-Visit MC Method)이라고 부릅니다.

위는 가치 함수를 추정하는 최초 접촉 MC 예측 알고리즘의 유사 코드입니다. 각 경험들은 실제 환경으로부터 얻은 거이기 때문에 당연히 편향이 없고, 큰 수의 법칙에 따라 추정값의 평균은 기댓값으로 수렴하게 됩니다. (추정 오류의 표준 편차는 $\frac{1}{\sqrt{n}}$만큼 감소, $n$은 샘플의 개수)
몬테카를로 행동 가치 추정
몬테카를로 방식으로 상태 가치 함수를 추정할 수 있음을 살펴봤는데요, 사실 상태 가치 함수를 추정한 결과는, 동역학을 모르는 상황에서는 어디에도 쓸 방도가 없습니다. 어떤 상태가 얼만큼 좋다는 정보만으로는 그 상태 사이의 연결을 해줄 수 있는 행동을 모르기 때문에 최적 정책 또한 알아낼 수 없습니다. 이 상황을 쉽게 해결할 수 있는 방법이 있는데요, 그것은 처음부터 행동 가치 함수를 추정하는 것입니다. 행동 가치 함수는 상태와 행동이 쌍으로 묶여 들어가는데요, 때문에 어떤 상태에서 무슨 행동을 했을 때, 그 가치 함수의 값이 높은지 바로 알 수 있기 때문에 정책을 결정할 수 있습니다. 따라서 몬테카를로 예측에서는 행동 가치 함수를 추정하는 것이 특히 유용합니다.
몬테카를로 제어
샘플링 기반 가치 함수가 추정 방법인 몬테카를로 예측에 대해 대략적으로 살펴봤습니다. 무한 개의 에피소드를 경험할 수 있다면, 각 경험에는 편향이 없기 때문에 정확한 가치 함수값을 추정할 수 있을 것입니다. 다만, 문제점은 샘플링 방식에서 모든 상태를 거칠 수 있음이 보장되지 않는다는 점입니다. 그렇기 때문에 특별한 가정을 추가하는데요, 그것은 에피소드가 하나의 상태-행동 쌍에서 시작하고, 모든 상태-행동 쌍이 에피소드가 시작하는 쌍으로서 선택될 확률이 0보다 크다는 가정입니다. 이를 시작 탐험(Exploring Start)의 가정이라고 부릅니다. 사실 당연히 모든 상태가 에피소드의 시작이 될 수는 없기 때문에 굉장히 비현실적인 가정인데요, 그럼에도 이러한 가정을 통해서 몬테카를로 예측을 사용한 정책 향상, 몬테카를로 제어가 최적 정책을 향해감을 증명할 수 있습니다.
\[\pi(s) \doteq \underset{a}{argmax}\space q(s, a)\]우리는 몬테카를로 예측에서 행동 가치 함수를 사용하기 때문에 탐욕적 정책을 만들 때 모델은 더 이상 필요하지 않습니다. 그리고 행동 가치 함수를 통해 탐욕적 정책을 만드는 것 자체도 굉장히 간단한데요, 특정 상태 $s$에서 선택할 수 있는 행동 중 가장 큰 가치 함수를 가지는 행동을 선택합니다.
\(q_{\pi_k}(s, \pi_{k+1}(s)) = q_{\pi_k}(s, \underset{a}{argmax}\space q_{\pi_k}(s, a))\) 다음 정책은 행동 가치 함수상에서 최고의 이득을 가져오는 행동으로 결정됩니다.
\(= \underset{a}{max}\space q_{\pi_k}(s, a)\) 즉, 상태 $s$의 행동 가치 함수 중에 최고의 가치를 반환하는 행동의 가치 함수의 값입니다.
\(\geq q_{\pi_k}(s, \pi_k(s))\) 당연히, 현재 정책대로 선택한 행동이 가지는 가치 함수의 값과 같거나 크겠습니다.
\[\geq v_{\pi_k}(s)\]그리고 그 값은, 상태 자체가 가지는 가치 함수보다는 크거나 같을 것입니다.
\(q_{\pi_k}(s, \pi_{k+1}(s)) \geq v_{\pi_k}(s)\) 위의 결론은 이전 포스팅에서 정책 향상 정리를 보이기 위한 조건이었습니다. 이를 통해 탐욕적 정책을 통한 정책 향상이 최적 정책과 최적 가치 함수로 수렴한다는 것을 알 수 있습니다. 이러한 과정을 따르는 알고리즘을 몬테카를로 ES(Monte Carlo Exploring Starts)라고 합니다.

시작 탐험 없는 몬테카를로 제어
시작 탐험을 가정한 몬테카를로 제어에서는 모든 상태를 경험하기 때문에 최적 정책으로의 수렴이 보장되었습니다. 하지만 시작 탐험은 다소 현실적이지 않은 가정입니다. 대부분의 환경에서는 모든 상태가 전부 시작 상태가 될 수 없기 때문입니다.
이러한 문제점을 해결하기 위한 두 가지 방법이 있습니다. 하나는 활성 정책(On-Policy) 방법이고, 다른 하나는 비활성 정책(Off-Policy) 방법입니다. 활성 정책 방법은 현재 결정을 내리는 정책을 평가하고 향상시키는 반면, 비활성 정책은 결정을 내리지 않는 정책을 평가하고 향상시킵니다. 일단은 활성 정책 방법에서 어떻게 최적 정책으로의 수렴이 보장되는지 살펴보겠습니다.
활성 정책 제어 방법의 대표적인 방법은 입실론 탐욕적 정책입니다. 활성 정책 제어 방법에서는 일반적으로 부드러운(soft) 정책을 가지는데요, 부드럽다는 말의 의미는 모든 행동에 대해서 0 이상의 확률이 부여된 상태이지만, 점점 결정론적인 최적 정책에 가깝게 이동한다는 뜻입니다. 입실론 탐욕적 정책에서는 대부분의 시간에서 최대의 행동 가치는 창출하는 행동을 선택하지만 일정 확률($\epsilon$)로 무작위 행동을 선택합니다.

정리하면 위와 같은 알고리즘인데요, 위와 같이 입실론이 껴 있을 때에도 정책 향상이 보장되는 지는 따로 보일 필요가 있습니다.
\(q_{\pi}(s, \pi'(s)) = \sum_{a}{\pi'(a|s)q_{\pi}(s, a)}\) 위 식은 바로 다음 행동만 새로운 정책 $\pi’$에 따라 선택하고, 그 다음 부터는 기존 정책 $\pi$에 따라 행동할 때의 행동 가치 함수입니다.
\[= \frac{\epsilon}{|\mathcal{A}(s)|}\sum_{a}{q_{\pi}(s, a) + (1-\epsilon)\space \underset{a}{max}\space q_{\pi}(s, a)}\]입실론 탐욕적 정책을 통해 선택될 다음 정책은 일단 입실론 만큼 동일한 확률로 모든 행동을 선택하고(첫 번째 항), 입실론을 제외한 확률만큼은 현재 구해진 행동 가치 함수상에서 최대 가치를 창출하는 행동을 선택하는 것입니다.
\(\geq \frac{\epsilon}{|\mathcal{A}(s)|}\sum_{a}{q_{\pi}(s, a) + (1-\epsilon)\sum_{a}{\frac{\pi(a|s) - \frac{\epsilon}{|\mathcal{A}(s)|}}{1-\epsilon}}}q_{\pi}(s, a)\) 그 값은, 기존 정책($\pi$)에 따라 선택했을 때보다는 당연히 큰 값을 가질 것입니다(최댓값을 선택한 것이기 때문에 당연한 사실).
\(= \frac{\epsilon}{|\mathcal{A}(s)|}\sum_{a}{q_{\pi}(s, a)} - \frac{\epsilon}{|\mathcal{A}(s)|}\sum_{a}{q_{\pi}(s, a)} + \sum_{a}{\pi(a|s)q_{\pi}(s, a)}\) $(1-\epsilon)$은 $a$와 관계가 없기 때문에 약분되어 사라지고, 식을 정리하면 위와 같습니다. 그리고 이는 아래와 같습니다.
\(= v_{\pi}(s)\) 위 유도 과정을 통해 정책 향상 정리의 조건이 만족되고, 위의 식에서 만약 등호가 성립한다면, 그게 곧 최적 정책임을 알 수 있습니다.
중요도추출법을 통한 비활성 정책 예측
위의 활성 정책 방법에서 눈여겨 봐야 하는 점은, 입실론 탐욕적 정책이라는 틀 안에서, 우리는 최적 정책이 아니라 근최적 정책을 위해 행동 가치 함수를 학습한다는 점입니다. 사실 샘플에 기반해 학습을 하는 방식에서는 탐험적 정책이 필수적입니다. 왜냐하면 다양한 행동을 해보아야 그 중에 무엇이 가장 좋은 방법인지 알 수 있기 때문입니다. 이를 위해서 활성 정책 방법에서는 입실론이라는 값을 두어 해당 값의 확률만큼 무작위로 행동을 선택하도록 했습니다.
비활성 정책 학습(Off-Policy Learning)에서는 행동을 선택하기 위해 사용되는 정책과 학습 대상 정책을 따로 두어 탐험 문제를 보다 분명하게 다룹니다. 행동을 선택하기 위해 사용되는 정책을 행동 정책(Behavior Policy, $b$)이라고 하고, 학습 대상이 되는 정책을 목표 정책(Target Policy, $\pi$)이라고 부릅니다. 그리고 행동 정책을 통해 생성된 데이터로부터 학습하는 이 전체 과정을 비활성 정책 학습이라고 부릅니다.
\[\pi(a|s) \gt0 \rightarrow b(a|s) \gt 0\]행동 정책으로부터 목표 정책의 가치를 추정하기 위해서는 행동 정책이 목표 정책의 모든 행동을 조금이라도 수행할 가능성이 있어야 합니다. 이를 보증(Coverage)의 가정이라고 부릅니다.
비활성 정책 방법을 사용할 때, 거의 대부분의 경우에는 중요도 추출법(Importance Sampling)을 사용합니다. 목표 정책과 행동 정책하에서 발생하는 상태-행동 궤적에 대한 상대적 확률을 중요도 추출 비율(Importance Sampling Ratio)이라고 합니다.
\[Pr\{A_t, S_{t+1}, A_{t+1}, ..., S_T|S_t, A_{t:T-1} \sim \pi \}\] \[= \pi(A_t|S_t)p(S_{t+1}|S_t, A_t)\pi(A_{t+1}|S_{t+1})...p(S_T|S_{T-1}, A_{T-1})\] \[= \prod_{k=t}^{T-1}\pi(A_k|S_k)p(S_k+1|S_k, A_k)\]위는 목표 정책 하에서 특정한 궤적이 발생할 확률입니다. 그리고 중요도 추출 비율은 아래와 같습니다.
\[\rho_{t:T-1} \doteq \frac{\prod_{k=t}^{T-1}\pi(A_k|S_k)p(S_k+1|S_k, A_k)}{\prod_{k=t}^{T-1}b(A_k|S_k)p(S_k+1|S_k, A_k)} = \prod_{k=t}^{T-1}\frac{\pi(A_k|S_k)}{b(A_k|S_k)}\]행동 정책으로부터 얻은 이득의 평균을 내면 당연히 행동 정책의 행동 가치 함수를 얻게 됩니다. 따라서 이득에 위의 중요도 추출 비율을 곱해주어 목표 정책의 행동 가치 함수를 구할 수 있도록 합니다.
\(\mathbb{E}[\rho_{t:T-1}G_t|S_t = s] = v_{\pi}(s)\) 위 식 자체는 평균을 구하는 건데, 샘플링 방식이 실제로 동작할 때와는 다소 거리가 있는 표현 방식입니다. 실제로 비활성 정책에서 중요도 추출법을 사용할 때에는 아래의 식을 사용합니다.
\(V(s) \doteq \frac{\sum_{t\in \mathcal{T(s)}}\rho_{t:T(t)-1}G_t}{|\mathcal{T(s)}|}\) 위의 식과 같이 단순히 평균을 내는 방식을 기본 중요도추출법(Ordinary Importance Sampling)이라고 합니다.
\(V(s) \doteq \frac{\sum_{t\in \mathcal{T(s)}}\rho_{t:T(t)-1}G_t}{\sum_{t\in \mathcal{T(s)}}\rho_{t:T(t)-1}}\) 위 식과 같이 상태 가치함수를 업데이트 하는 방식을 가중치 중요도추출법(Weighted Importance Sampling)이라고 부릅니다. 위 방식과 기본 중요도 추출법의 차이는 편차와 분산에 있습니다. 기본 중요도추출법은 편차가 없는 대신 분산이 크고, 가중치 중요도추출법은 편차가 있는 대신, 분산이 작습니다. 가중치 중요도추출법의 편차는 단일 이득에 대해서 생각해보면 명확히 드러납니다. 행동 정책으로부터 추출한 한 개의 이득이 있다면, 가중치 중요도추출법에 따르면 해당 값이 곧 목표 정책의 추정값이 됩니다.
무한 분산
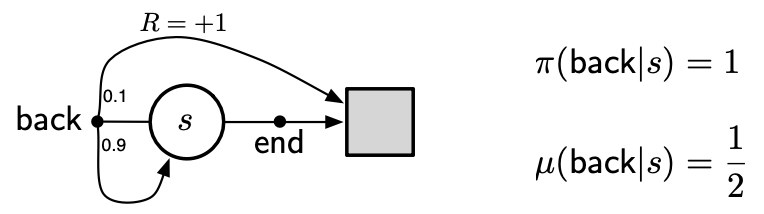
import numpy as np
N = 1000000
V_ordinary = 0.0
V_weighted = 0.0
Cumulative_W = 0.0
max_episode_length = 10000
for episode_num in range(1, N + 1):
state =
W = 1.0
G = 0.0
t = 0
while state != 'terminal' and t < max_episode_length:
t += 1
action = np.random.choice(['left', 'right'], p=[0.5, 0.5])
if action == 'left':
if np.random.rand() < 0.1:
next_state = 'terminal'
reward = 1
else:
next_state = 's'
reward = 0
else: # action == 'right'
next_state = 'terminal'
reward = 0
G += reward
pi = 1.0 if action == 'left' else 0.0
b = 0.5
if pi == 0.0:
W = 0.0
break
else:
W *= pi / b
state = next_state
V_ordinary += W * G
Cumulative_W += W
V_weighted += W * G
V_ordinary_estimate = V_ordinary / N
V_weighted_estimate = V_weighted / Cumulative_W if Cumulative_W != 0 else 0.0
print("Estimated V(s) using ordinary importance sampling:", V_ordinary_estimate)
print("Estimated V(s) using weighted importance sampling:", V_weighted_estimate)
위 코드를 실행시켜보면 기본 중요도추출법과 가중치 중요도추출법을 사용해 상태 가치 함수를 계산할 수 있는데요, 가중치 중요도추출법에서는, 이득이 1이 아닌 모든 경우는 추정값에 기여할 수 없기 때문에 항상 정확히 1의 값을 얻게 됩니다(max_episode_length 내에 끝나지 않는 에피소드가 존재하는 경우에는, 값이 1이 아닐 수 있음).
댓글남기기