강화학습 04: 동적 프로그래밍
글에 들어가기 앞서…
이 포스팅은 ‘강화학습‘에 대한 내용을 담고 있습니다.
자료 출처: 단단한 강화학습, Reinforcement Learning An Introduction , 2nd edition. 리처드 서튼, 앤드류 바트로, 김성우(옮긴이)
동적 프로그래밍
동적 프로그래밍(Dynamic Programming)은 환경이 완전히 주어졌을 때, 최적 정책을 계산하기 위해 사용될 수 있는 알고리즘입니다. 이 포스팅에서는 유한 MDP 환경에서 동적 프로그래밍을 사용하는 내용을 다룹니다. 연속된 공간에서 정의된 MDP 환경에서도 동적 프로그래밍을 사용할 수 있지만, 정확한 해는 오직 특별한 경우에만 구할 수 있습니다.
MDP문제에서 벨만 방정식과 최적 벨만 방정식으로부터 해석적으로 최적 정책을 구할 수 있다는 내용을 이전 포스팅에서 다루었습니다. 하지만 이 접근방식은 거의 대부분의 경우에 실용적이지 않습니다. 그렇지만, 벨만 방정식은 여전히 강화학습에서 강력한 도구로 사용되는데요, 이 포스팅에서는 할당이라는 방법을 사용해 벨만 방정식으로부터 동적 프로그래밍 알고리즘을 얻어냅니다.
정책 평가
\[v_{\pi}(s) \doteq \sum_a\pi(a|s)\sum_{s', r}p(s', r|s, a)[r + \gamma v_{\pi}(s')]\]위 식은 MDP 문제에서 얻을 수 있는 상태 가치 함수입니다. 위 식에서 $\gamma$가 1보다 작은 양수를 만족하거나, 정책 $\pi$를 따르는 모든 상태가 종국적으로(Ultimately) 더 이상 변하지 않는 상태에 도달한다는 것이 담보된다면 상태 가치 함수의 존재와 유일성이 보장됩니다. 상태 가치 함수의 개수가 상태의 개수만큼 있는 연립방정식을 풀면 상태 가치 함수를 구할 수는 있지만, 다소 실용적이지 못한 접근 방식입니다. 강화학습 문제를 해결하기 위해서는 반복 해법(Iterative Solution Method)으로 푸는 것이 적합합니다.
위에서 언급한 상태 가치 함수의 존재와 유일성을 보장하는 조건이 만족되는 상황에서는 무한한 반복 할당을 통해 상태 가치 함수에 도달할 수 있음이 증명되어 있습니다. 이 사실을 이용해 반복 해법을 통해 가치 함수를 구해내는 방법을 반복 정책 평가(Iterative Policy Evaluation)라고 부릅니다.
\[v_{k+1}(s) \doteq \sum_a\pi(a|s)\sum_{s', r}p(s', r|s, a)[r + \gamma v_{k}(s')]\]상태 가치 함수의 아랫첨자가 바뀌었는데요, $\pi$ 대신에 인덱스로 대체된 것을 확인할 수 있습니다. 여기서 상태 가치 함수는 여전히 $\pi$를 따릅니다. 위의 식에서 확인할 수 있는 것은, 상태 가치 함수를 갱신할 때, 이후 상태들의 표본이 아니라 기댓값으로 갱신한다는 점입니다. 이것은 환경의 동역학이 주어져 있기 때문에 가능한 일인데요, 이로 인해 동적 프로그래밍에서 수행되는 모든 갱신은 기댓값 갱신(Expected Update)이라고 불립니다.
인덱스가 계속 늘어나면서 상태 가치 함수는 점점 $v_{\pi}(s)$에 가까워질 텐데요, 배열 두 개만 있으면 반복 정책 평가를 구현할 수 있습니다. 배열 하나는 이전 상태 가치 함수를 위한 것이고, 다른 또 하나의 배열은 이후 상태 가치 함수를 저장하기 위한 것입니다. 그런데, 대부분의 경우에 상태의 개수가 굉장히 많은데요, 상태의 개수만큼 저장할 수 있는 배열을 한 개만 쓰는 것도 꽤나 힘든 일입니다. 하물며 동일한 크기의 배열을 두 개를 만들어 사용하는 것은 꽤나 곤란할 수 있습니다. 사실 배열이 꼭 두 개가 필요하진 않습니다. 새로운 가치가 이전 가치를 덮어씌우는 방식으로 구현되어도 전혀 문제가 발생하지 않고, 그렇게 갱신하는 것이 더 쉽고 심지어는 더 빠르게 수렴합니다. 새로운 데이터가 생기자마자 바로 이를 이용하기 때문입니다. 갱신은 상태 공간에 대해 일괄적으로(Sweep)하는 방식을 사용하는데요, 포스팅 뒷 부분에서 다룰 내용이지만 반드시 그럴 필요는 없습니다.

위는 반복 정책 평가 알고리즘입니다. 무한 번 반복 할당을 통해 완벽한 $v_{\pi}(s)$를 구하기 보단, 실전적으로는 적당한 임계값 이하로 변화량이 줄어들면 알고리즘이 종료됩니다.
예시 1) 4 by 4 Grid World
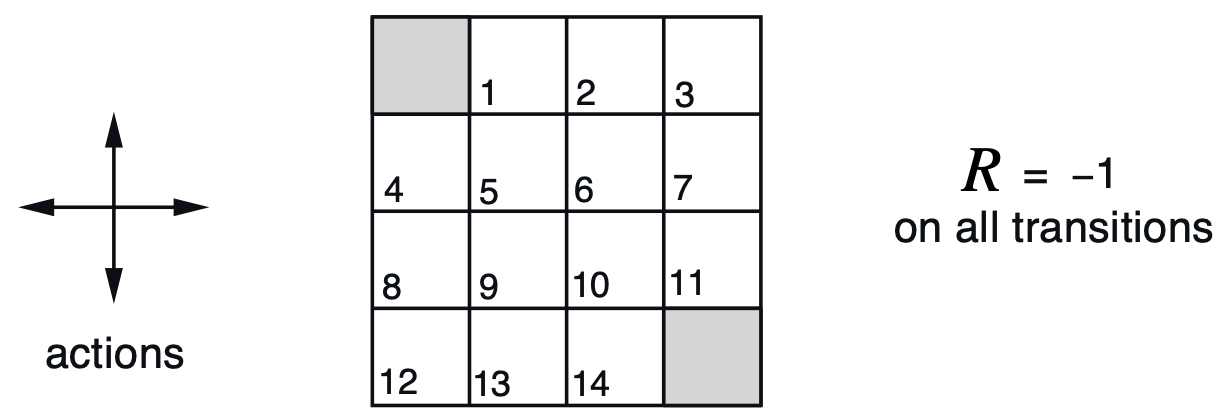
가로 세로 4개의 칸으로 구성된, 총 16개의 상태 공간으로 구성되어 있습니다. 회색 칸을 제외한 14개의 비종단 상태가 있고, 회색 칸에 도착하면 에피소드가 종료됩니다.
import numpy as np
import copy, time
n = 4
state = [[0 for i in range(n)] for j in range(n)]
nx_L = [-1,1,0,0]
ny_L = [0,0,1,-1]
state_copy = copy.deepcopy(state)
direction_L = ['up','down','right','left']
w = 100 #hyperparameter
for k in range(w):
for i in range(n):
for j in range(n):
tmp = 0
reward = -1
for next in range(4):
if (i == 0 and j == 0) or (i == n-1 and j == n-1) :
break
if (i+nx_L[next] >= n or j+ny_L[next] >= n) or (i+nx_L[next] < 0 or j+ny_L[next] < 0):
tmp = tmp + 0.25 * (reward + state[i][j])
continue
tmp = tmp + 0.25 * (reward + state[i+nx_L[next]][j+ny_L[next]])
state_copy[i][j] = tmp
state = copy.deepcopy(state_copy)
if k % 10 == 0 :
print(f'iteration {k} :')
print(state)
위 코드는 무작위 정책을 따를 때, 16칸의 상태 가치 함수를 반복 정책 평가 방식으로 구하도록 구현된 파이썬 코드입니다.
정책 향상
반복 해법을 통해 가치 함수를 계산할 수 있다는 점을 살펴봤는데요, 돌이켜 생각해 보면 사실 가치 함수를 계산하는 이유는 좋은 정책을 찾기 위함입니다. 어떤 정책에 대해 가치 함수를 구했다면, 이 값을 통해 더 나은 정책을 확정적으로 구할 수 있는 방법이 존재할까요? 만약 그렇다면, 그걸 구하는 반복 해법은 존재할까요?
\[q_{\pi}(s, \pi'(s))\geq v_{\pi}(s)\]위 식의 의미는, 기본적으로 정책 $\pi$를 따르는데 상태 $s$에서만 정책 $\pi’$를 따르게 하는 상황을 의미합니다(행동 가치 함수를 계산할 때, 기준이 되는 정책은 $\pi$). 이를 모든 상태에 대해 만족시킬 수 있는 정책 $\pi’$이 존재한다고 가정해 보겠습니다. 일단 $\pi’$가 $\pi$보다 좋다는 사실을 아래의 유도를 통해 명확히 알 수 있습니다.
\[v_{\pi}(s) \leq q_{\pi}(s, \pi'(s))\] \[= \mathbb{E}[R_{t+1} + \gamma v_{\pi}(S_{t+1})|S_t = s, A_t = \pi'(s)]\]\(= \mathbb{E}_{\pi'}[R_{t+1} + \gamma v_{\pi}(S_{t+1})|S_t = s]\) 조건부에서 행동 확률 변수를 제외하는 대신, $\mathbb{E}$의 아랫첨자에 이를 추가합니다.
\[\leq \mathbb{E}_{\pi'}[R_{t+1} + \gamma q_{\pi}(S_{t+1}, \pi'(S_{t+1}))|S_t = s]\]\(= \mathbb{E}_{\pi'}[R_{t+1} + \gamma \mathbb{E}_{\pi'}[R_{t+2} + \gamma v_{\pi}(S_{t+2})|S_{t+1}, A_{t+1} = \pi'(S_{t+1})]|S_t = s]\) 이미 기댓값 함수에서 $\pi’$를 명시하고 있기 때문에 조건부로부터 독립적입니다. 따라서 기댓값 함수를 없앨 수 있습니다.
\[= \mathbb{E}_{\pi'}[R_{t+1} + \gamma R_{t+2} + \gamma^2v_{\pi}(S_{t+2})|S_t = s]\] \[\cdot \cdot \cdot\] \[= \mathbb{E}_{\pi'}[R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3} + \gamma^3R_{t+4} + \cdot \cdot \cdot \space|S_t = s]\] \[= v_{\pi'}(s)\]결론적으로 모든 상태에 대해 $q_{\pi}(s, \pi’(s))\geq v_{\pi}(s)$를 만족시키는 정책이 있다면, 해당 정책은 확실하게 더 나은 정책입니다. 그렇다면, $q_{\pi}(s, \pi’(s))\geq v_{\pi}(s)$를 만족시키는 정책은 어떻게 구할 수 있을까요? 행동 가치 함수가 구해졌다면, 탐욕적 행동 선택을 통해 손쉽게 $\pi’$를 얻어낼 수 있습니다.
\[\pi'(s) = \underset{a}{argmax}\space q_{\pi}(s, a)\] \[= \underset{a}{argmax}\space \mathbb{E}[R_{t+1} + \gamma v_{\pi}(S_{t+1}) | S_t = s, A_t = a]\] \[= \underset{a}{argmax}\space \sum_{s', r}p(s', r|s, a)[r + \gamma v_{\pi}(s')]\]위와 같은 탐욕적 정책은 원래의 정책 이상 이상으로 좋은 결과를 가져옵니다. 이렇게 기존 정책 가치 함수에 대해 탐욕적이게 해 기존 정책을 능가하는 새로운 정책을 만드는 과정을 정책 향상(Policy Improvement)이라고 부릅니다.
새로운 탐욕적 정책이 기존 정책을 능가시키지 못하고 기존 정책과 같은 수준을 유지한다면, 아래의 최적 벨만 방정식을 만족합니다.
\[v_{\pi'}(s) = \underset{a}{max} \space \mathbb{E}[R_{t+1} + \gamma v_{\pi'}(S_{t+1}|S_t = s, A_t = a)]\] \[= \underset{a}{max} \sum_{s', r} p(s', r | s, a)[r + \gamma v_{\pi'}(s')]\]따라서 만약 정책 향상이 일어나지 않는다면 그 자체로 최적 정책에 도달했음을 알 수 있습니다.
정책 반복, 가치 반복
가치 함수를 구하는 정책 평가와 가치 함수를 통해 정책을 향상시키는 방법을 모두 다루었기 때문에 계속 더 나은 정책을 구해내는 알고리즘을 만들 수 있습니다. 정책의 완전한 평가(정책에 대해 거의 정확한 가치 함수를 구함)와 정책 향상을 번갈아가면서 최적 정책 및 최적 가치 함수를 구하는 방식을 정책 반복(Policy Iteration)이라고 부릅니다.

4 by 4 Grid World 예시를 통해 알 수 있는 사실은, 우리가 꼭 완전한 가치 함수를 구할 필요는 없다는 점입니다. 몇 번 안되는 반복을 통해 구해진 가치 함수를 통해서도 최적 정책을 구할 수 있었습니다. 정책 평가를 정밀한 수준까지 도달하지 않고 중간에 멈추는 것을 중단된 정책 평가(Truncated Policy Evaluation)라고 부릅니다. 그리고 중단된 정책 평가와 정책 향상을 결합한 알고리즘을 가치 반복(Value Iteration)이라고 합니다.
\[v_{k+1}(s) \doteq \underset{a}{max} \space \mathbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) | S_t = s, A_t =a]\] \[= \underset{a}{max} \space \sum_{s', r}p(s', r | s, a)[r + \gamma v_k(s')]\]위의 식이 의미하는 바는, 한 번의 정책 평가 이후에 정책 향상을 바로 수행하는 것입니다. 이러한 방식을 통해서도 정책은 여전히 최적 정책에 수렴합니다. 그리고 식의 형태가 최적 벨만 방정식과 동일한데, 최적 벨만 방정식을 갱신 규칙으로 바꾸기만 하면 가치 반복을 위한 식이 됩니다. 아래는 가치 반복 알고리즘입니다.
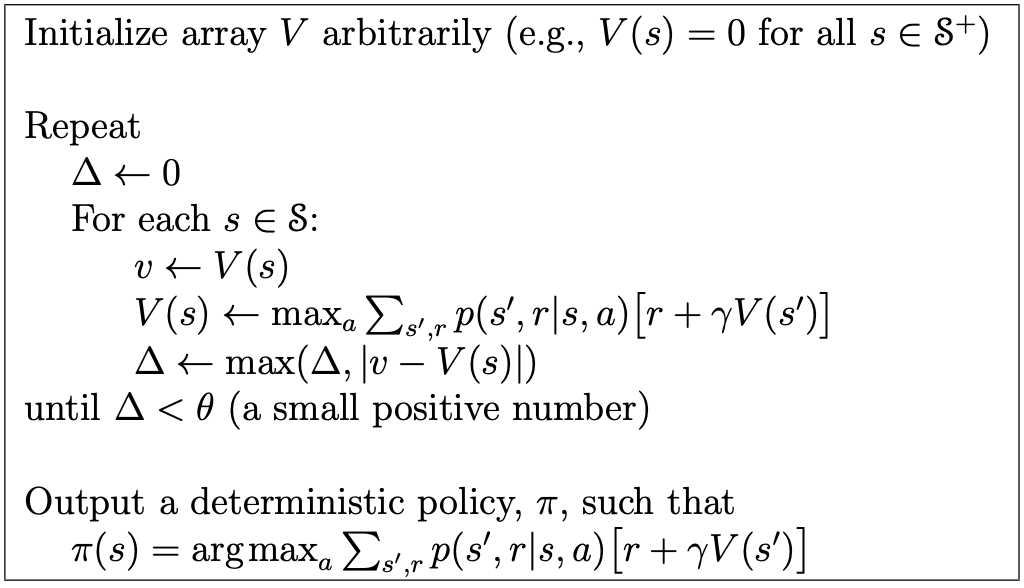
아무튼 위와 같이 정책 평가와 정책 향상의 반복 주기는 다양하게 설정될 수 있는데요, 세부 사항과 관계없이 이 두 과정이 서로 상호작용하는 일반적인 방법을 일반화된 정책 반복(GPI, Generalized Policy Iteration)이라고 부릅니다.
예시 2) 자동차 렌탈
이 문제의 주인공 잭은 렌트카 사업을 하는데요, 총 두 곳의 지점을 운영합니다. 차를 빌려주면 10달러의 보상을 받습니다. 해당 지점에 빌려줄 차가 없으면 보상을 받지 못합니다. 잭은 밤사이 두 지점의 차량을 한 대당 2달러의 비용을 들여 교환할 수 있습니다.(하루에 교환할 수 있는 최대 자동차의 개수는 5대입니다.) 한 지점에서 대여되고 반납되는 자동차의 개수는 푸아송 분포를 따릅니다. 대여되는 자동차 개수에 대한 $\lambda$값은 첫 번째와 두 번째 지점에서 각각 3, 4대이고, 회수되는 자동차의 개수는 각각 3, 2대입니다. 각 지점은 최대 20대까지만 자동차를 보유할 수 있습니다. 할인율을 $\gamma = 0.9$로 할 때, 정책 반복을 통해 최적 정책을 구해보겠습니다.
아래는 정책 반복을 통해 최적 정책을 구해주는 파이썬 코드입니다.
import numpy as np
from scipy.stats import poisson
# Problem parameters
max_cars = 20 # Maximum cars at each location
max_move_cars = 5 # Maximum cars to move overnight
rental_reward = 10 # Reward per car rented
move_cost = 2 # Cost per car moved
gamma = 0.9 # Discount factor
theta = 1e-4 # Threshold for convergence
# Poisson distribution parameters
request_lambda = [3, 4] # Rental requests at first and second location
return_lambda = [3, 2] # Returns at first and second location
# Precompute Poisson probabilities up to a reasonable limit
poisson_upper_bound = 11 # Upper limit for Poisson distribution
poisson_cache = dict()
def poisson_prob(n, lam):
key = (n, lam)
if key not in poisson_cache:
poisson_cache[key] = poisson.pmf(n, lam)
return poisson_cache[key]
# Initialize state-value function and policy
value = np.zeros((max_cars + 1, max_cars + 1))
policy = np.zeros_like(value, dtype=int) # Initial policy: do nothing
# Possible actions: transfer up to max_move_cars cars
actions = np.arange(-max_move_cars, max_move_cars + 1)
# Policy Evaluation
def policy_evaluation(policy, value):
iteration = 0
while True:
delta = 0
new_value = np.copy(value)
for i in range(max_cars + 1):
for j in range(max_cars + 1):
state = [i, j]
action = policy[i, j]
action = max(-j, min(i, action)) # Respect the constraints
# Immediate cost for moving cars
move_cost_total = abs(action) * move_cost
# Number of cars at each location after moving cars
num_cars_loc1 = min(i - action, max_cars)
num_cars_loc2 = min(j + action, max_cars)
# Expected returns
expected_return = -move_cost_total
# Iterate over possible rental requests at both locations
for rental_request_loc1 in range(poisson_upper_bound):
for rental_request_loc2 in range(poisson_upper_bound):
prob_rental_loc1 = poisson_prob(rental_request_loc1, request_lambda[0])
prob_rental_loc2 = poisson_prob(rental_request_loc2, request_lambda[1])
prob_rental = prob_rental_loc1 * prob_rental_loc2
# Actual rentals are limited by the number of cars available
rentals_loc1 = min(num_cars_loc1, rental_request_loc1)
rentals_loc2 = min(num_cars_loc2, rental_request_loc2)
# Rewards from rentals
reward = (rentals_loc1 + rentals_loc2) * rental_reward
# Cars remaining after rentals
cars_loc1 = num_cars_loc1 - rentals_loc1
cars_loc2 = num_cars_loc2 - rentals_loc2
# Iterate over possible returns at both locations
for returns_loc1 in range(poisson_upper_bound):
for returns_loc2 in range(poisson_upper_bound):
prob_return_loc1 = poisson_prob(returns_loc1, return_lambda[0])
prob_return_loc2 = poisson_prob(returns_loc2, return_lambda[1])
prob_return = prob_return_loc1 * prob_return_loc2
# Total probability
prob = prob_rental * prob_return
# Cars after returns
cars_loc1_ = min(cars_loc1 + returns_loc1, max_cars)
cars_loc2_ = min(cars_loc2 + returns_loc2, max_cars)
# Update expected return
expected_return += prob * (reward + gamma * value[cars_loc1_, cars_loc2_])
# Update the value function
new_value[i, j] = expected_return
delta = max(delta, abs(new_value[i, j] - value[i, j]))
value = new_value
iteration += 1
print(f'Policy Evaluation Iteration: {iteration}, Delta: {delta}')
if delta < theta:
break
return value
# Run policy evaluation
value = policy_evaluation(policy, value)
print("Final state-value function:")
print(value)
비동기 동적 프로그래밍
포스팅 앞쪽에서 언급했다시피, 사실 동적 프로그래밍을 통해 정책 평가를 하는 과정에서 반드시 일괄적인 방식으로 갱신할 필요는 없습니다. 오히려 상태가 굉장히 많은 게임인 경우 이런 방식의 업데이트는 현실적이지 않습니다. 비동기(Asynchronous) 동적 프로그래밍 알고리즘은 상태 집합에 대해 체계적인 일괄 계산을 수행하지 않는 개별적인(in-place) 반복 동적 프로그래밍 알고리즘입니다.
이 알고리즘에서는 상태의 가치가 갱신하는 순서가 무엇이든 다른 상태의 가치를 이용할 수 있는 상황이라면 갱신합니다. 비동기 동적 프로그래밍 알고리즘 역시 수렴성이 보장되는데요, $\gamma$가 $[0, 1)$일 때, 그리고 모든 상태가 무한 번 발생한다는 조건이 만족될 때 수렴성이 보장됩니다. 이런 방식의 알고리즘을 실시간 학습에 훨씬 유리합니다. 왜냐하면 에이전트가 실제로 MDP를 경함하면서 동시에 반복적 동적 프로그래밍 알고리즘을 수행할 수 있기 때문입니다. 실제로는 상태가 굉장히 많은 문제가 대부분이기 때문에, 이런 방식을 통한 학습이 실용적입니다.
댓글남기기