SPLIT: SE(3)-diffusion via Local Geometiry-based Score Prediction for 3D Scene-to-Pose-Set Matching Problems

이 포스팅은 ‘SPLIT: SE(3)-diffusion via Local Geometiry-based Score Prediction for 3D Scene-to-Pose-Set Matching Problems‘에 대한 내용을 담고 있습니다.

논문 주소: https://arxiv.org/pdf/2411.10049

SPLIT: SE(3)-diffusion via Local Geometiry-based Score Prediction for 3D Scene-to-Pose-Set Matching Problems

특정 태스크를 수행할 때, 말단부의 포즈를 추론하는 일은 항상 중요하면서도 잘 해결되지 않는 문제입니다. 가장 전통적인 방법에서는 특정 태스크를 수행하기 위한 모든 세부적인 알고리즘을 설정하고, 이 알고리즘들의 조합으로 태스크를 해결했습니다. 당연히 잘 동작하지 않았고요, 여러 다양한 태스크들에 일반적으로 사용될 수 없다는 문제점이 있습니다.

요즘 많이 사용되는 학습 기반 방법론으로 접근해도 적절한 포즈를 추론하는 일은 쉽게 해결되지 않습니다. 학습 기반 방식에서는 먼저 물체를 이미지에서 찾고, 찾은 물체에서 들기 쉬워보이는 부분들인 Keypoints를 검출합니다. 그리고 이 Keypoints에 적절한 포즈를 추론하는데요, 이 Keypoints가 제대로 찾아지지 않으면 그 다음 단계인 포즈 검출도 이상하게 되기 때문에 Keypoints를 잘 찾는게 굉장히 중요합니다. 그런데 문제는 이게 잘 안됩니다. 때문에 최근에는 Keypoints를 찾지 않고, 바로 포즈를 추론하는 접근법이 더 선호됩니다.

이 논문에서는 다양한 태스크에 모두 적용될 수 있도록 SPLIT(Score Prediction with Local Geometry Information for Rigid Transformation)이라는 새로운 모델을 제안합니다. 이 SPLIT에서는 Score-based Generative Model을 사용해, 랜덤한 노이즈로부터 점점 태스크 성공 확률이 높은 포즈를 검출해 나갑니다. 구체적으로 이 모델이 어떻게 구성돼 있는지 아래에서 살펴봅니다.

Introduction

전통적인 방법들은 다양한 태스크를 범용적으로 수행하는데 큰 어려움이 있습니다. 왜냐하면 개별적인 알고리즘들을 조합하는 방식으로 태스크를 해결했기 때문입니다. 일반적으로 잘 동작하게 만들기 위해서는 이전과는 다른 접근이 필요합니다.

이 논문에서는 3D scene-to-pose-set matching 이라는 새로운 문제를 정의합니다. 이 문제 정의에서는 기하학적인 특징은 물체의 전역적인 형태가 아니라, 국소적인 형태에 의해 결정된다고 가정하고 이를 Spatial Locality 라고 부릅니다. 예를 들어, 우리가 컵을 들어올리는 태스크를 수행한다고 할 때, 로봇이 컵을 잡을 특정한 부분의 모양만 알면 되지, 컵 전체의 모양이 크게 중요하지는 않습니다. 그리고 이런 접근 방식, Spatial Locality만을 보고 포즈를 결정하는 방식은 사전 지식을 필요로 하지 않는, 좀 더 유연한 프레임워크를 제공합니다.

Preliminaries

SPLIT 모델에서 사용되는 배경 지식을 먼저 살펴봅니다.

Score-based Generative Models

이 논문에서는 성공 확률이 높은 포즈를 추론하기 위해 SGM(Score-based Generative Model)을 사용합니다. SGM도 랜덤 노이즈를 시작으로 점차 성공 확률이 높은 포즈를 찾아가는 방식으로 반복적인 샘플링이 수행하는 일종의 확산 모델입니다.

\[\mathcal{L}_{\mathrm{DSM}} = \frac{1}{L} \sum_{k=0}^{L} \mathbb{E}_{x, \tilde{x}} \Bigl[ \bigl\| s_{\theta}(\tilde{x}) - \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x} \mid x) \bigr\|_2^2 \Bigr]\] \[q_{\sigma}(\tilde{x} \mid x) = \mathcal{N}(\tilde x ; x, \sigma^2I)\] \[x_{k-1} = x_k + \frac{\alpha_k}{2}s_{\theta}\bigl(x_k, \sigma_k\bigr) + \sqrt{\alpha_k}\,\epsilon, \quad \epsilon \sim \mathcal{N}(0, I). \quad \text{(Langevin Dynamics)}\]

손실함수에서 알 수 있는 것은, 이 모델에서 학습하는 것은 ‘노이즈가 어떤 방향으로 추가되었는가?’ 입니다. 정확하게는 원레 데이터로 복원하도록 하는 반대방향을 학습합니다. 기울기에 대해 제대로 학습이 됐다면, 랭주뱅 동역학(Langegin Dynamics)을 통해 업데이트를 수행합니다.

• https://yang-song.net/blog/2021/score/

위 도식은 랭주뱅 동역학이 일어나는 과정을 직관적으로 보여줍니다. 시간이 지남에 따라 모이는 점들이 물체를 잡을 성공 확률이 높은 지점이 됩니다. 풀리지 않는 의문은 물체를 잡을 성공 확률이 높은 지점으로 이동하게 하는 기울기를 어떻게 구하는가 입니다. 말단부의 포즈는 4 by 4의 동차행렬로 표현되는데, 이 동차행렬의 공간에서 성공 확률이 높은 포즈로의 이동 방향, 기울기를 형식적으로 나타낼 수 있어야 합니다.

SE(3) Lie Group

로보틱스에서 물체의 자세는 4 by 4의 동차행렬로 표현될 수 있습니다. 이 동차행렬은 수학적으로 모든 부분에서 미분 가능한 manifold로 SE(3)이라고도 표현됩니다. 특정 자세 H는 이 manifold 상의 공간을 돌아다닐 텐데요, 특정 자세 H에서 SE(3)에 대한 접공간(Tangent Space)을 아래와 같이 표현합니다.

\[T_HSE(3) \in \mathbb R^6\]

그리고 특히 이동을 하지 않는, 단위 행렬인 동차 행렬 $\varepsilon$에서의 접공간을 아래와 같이 표현합니다.

\[\mathfrak {se}(3):= T_\varepsilon SE(3) \in \mathbb R^6\]

단위 행렬의 접공간과 동차행렬 공간 사이의 mapping을 아래와 같이 정의할 수 있고, 이 논문에서는 이를 Global Parameterization 이라고 합니다.

\[\text{Exp}: \mathbb R^6 \rightarrow SE(3)\] \[\text{Log}: SE(3)\rightarrow \mathbb R^6\]

비슷하게 Local Parmeterization을 정의할 수 있습니다. Global Parameterization이 단위 행렬에서의 접공간 mapping한 거라면, Local Parameterization은 동차행렬 H의 접공간에 mapping 시킵니다. 그리고 동차행렬 공간에서 H와 단위 행렬 사이의 변환을 할 수 있기 때문에, Local Parameterization은 아래와 같이 Global Parameterization을 사용해 표현될 수 있습니다.

\[{^H}\text{Exp}(h') := H\text{Exp}(h')\] \[{^H}\text{Log}(H') := \text{Log}(H^{-1}H')\] \[where \quad h' = {^H}\text{Log}(H')\]

동차행렬 공간에서의 가우시안 분포를 어떻게 정의를 해야합니다. 왜냐하면 동차행렬로 주어진 한 점에 계속해서 가우시안 노이즈를 더해나갈 것이기 때문이죠. 그런데 위와 같이 동차행렬 공간과 6차원 실수공간 사이의 관계를 정의하고 나면, 동차행렬 공간에서의 가우시안 분포를 정의할 수 있습니다.

\[q\bigl(H \mid \overline{H}, \Sigma\bigr) \;\propto\; \exp\!\Bigl( -0.5 \,\bigl\|{^\overline{H} }\,\mathrm{Log}(H)\bigr\|_{\Sigma^{-1}}^2 \Bigr).\] \[q_\sigma(H \mid \bar H) \quad \text{where} \quad \Sigma = \sigma I\]

주된 아이디어는 동차행렬 공간에서 바로 가우시안 분포를 정의하는게 아니라, ‘동차행렬을 실수 공간으로 옮긴 뒤, 실수공간에서 가우시안 분포를 적용시켜 다시 동차행렬 공간으로 옮긴다’ 입니다.

\[{^H}\nabla f(H') = \frac{ {^H}D f(H)}{DH} \big|_{H=H'} = \frac{ \partial f(h)}{\partial h} \big|_{h=h'}\] \[h' = {^H} \mathrm{Log}(H').\]

그리고 위와 같이 동차행렬 공간의 특정 포즈가 입력으로 들어가는 함수의 기울기도 구할 수 있습니다.

Method

위의 Preliminaries에서 다룬 내용들을 바탕으로 SPLIT 모델을 제안합니다.

3D Scene-to-pose-set matching: Towards a Generalizable Pose Detection Formulation(문제 정의)

먼저 3D Scene-to-pose-set matching 이라는 새로운 문제를 정의합니다. 이 문제에는 중요한 가정 두 가지가 있는데, 아래와 같습니다.

• 목표 포즈는 장면의 특정 부분, 국부 기하 정보와만 관계가 있다(=Local Geometric Context).

• 동일한 국부 기하 정보는 동일한 포즈를 유도한다.

\[\mathcal F_\phi(H, X) = {^H}z\]

위에서 H는 특정 자세, 그리고 X는 전체 장면을 의미합니다. 그런데 문제 가정에 따르면 전체 장면의 정보는 필요하지 않습니다. 따라서 위의 함수를 사용해 H 주변의 국부 기하 정보로 변환합니다.

\[p(\text{succ} \mid H, X) = p(\text{succ} \mid {^H}z)\]

그리고, 특정 장면과 자세에서 잡기를 성공할 확률은, 오직 이 국부 기하 정보만을 바탕으로 구할 수 있습니다.

SPLIT: Sample-frame Score Prediction based on the Local Geometry

이제 이 3D Scene-to-pose-set matching문제를 어떻게 SE(3)-확산 모델로 해결할 수 있는지 설명합니다. 우리의 목적은 포즈를 찾아내는 건데요, 아무 포즈를 찾아내는게 아니라 특정 장면에서 성공할 수 있는 포즈를 찾아내는게 우리의 목적입니다.

\[H \sim p(H \mid \text{succ}, X)\]

말하자면, 위의 분포를 찾아내고, 이 분포에서 H를 뽑아내야 합니다. 문제는 바로 위의 포즈 분포를 바로 알 수 없다는 점입니다. 그렇기 때문에 처음에 아무런 점들이나 흩뿌려 놓고, 포즈 분포의 기울기인 $s(H, X)$ 라는 스코어 함수를 따라 조금씩 이동시키는 확산 모델 방법론을 사용합니다. 그런데, 포즈 분포를 알지 못하기 때문에 포즈 분포의 기울기인 스코어 함수는 학습을 통해 구합니다.

\[s(H, X) = \nabla \log p(H \mid \text{succ}, X)\] \[= \nabla \log \frac{p(\text{succ} \mid H, X)p(H \mid X)}{p(\text{succ} \mid X)}\] \[= \nabla \log p(\text{succ} \mid H, X)\] \[= \nabla \log p(\text{succ} \mid {^H}z)\]

그리고 성공할 수 있는 포즈 확률의 기울기 대신 해당 조건부 확률의 우도의 기울기로 대신 구할 수 있습니다. 그리고 문제의 정의에 따라 조건부의 H, X 를 Local Geometric Context로 대체합니다. 아무튼 스코어 함수를 구하기 위해서는 동차 행렬의 분포에 대한 기울기를 구해야 합니다.

\[\log p(H | \text{succ}, X) := f(H)\] \[{^\varepsilon }\nabla f(H) = \frac{\partial f(h)}{\partial h} = \frac{\partial f(Log(H))}{\partial h}\] \[{^H }\nabla f(H) = \frac{\partial s(h)}{\partial h} = \frac{\partial f({^H } Log(H))}{\partial h}\]

그런데 스코어 함수를 구할 때, global parameterization을 사용하면 스코어 함수는 현재의 위치인 H에 따라 값이 결정됩니다. 반면에, local parameterization을 사용하면 스코어 함수를 구할 때, 현재 위치가 스코어 예측에 사용되지 않습니다. 따라서 이 모델에서는 현재 위치의 local parameterization을 사용합니다. 이런 아이디어를 바탕으로 아래의 스코어 함수 예측이 수행됩니다.

\[\mathcal F_\phi(H, X) = {^H}z\] \[s_\theta({^H}z) \simeq {^H}\nabla \log p(H \mid \text{succ}, X)\]

위와 같이 local parameterization에 대해 예측을 하도록 해두면 예측이 훨씬 쉬워지고, 모든 포즈에 대해 동일하게 대칭되게 학습할 수 있습니다.

Network Architecture for SPLIT

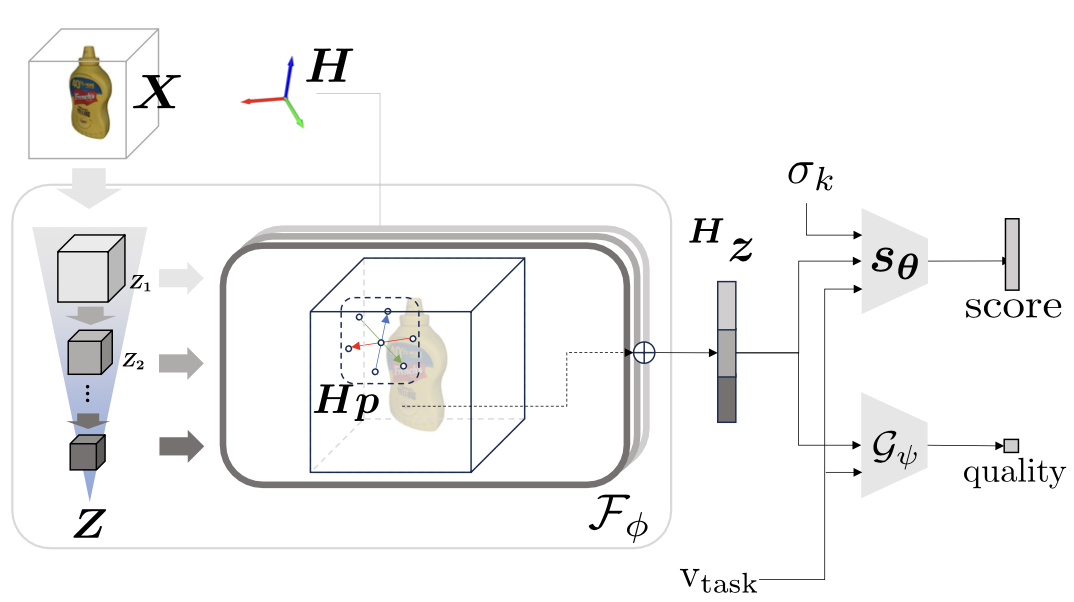
X는 Occupancy Grid로 얻어지는데, 깊이 이미지를 일단 point cloud로 바꾼 다음, 미리 정해둔 그리드 맵에 따라 작성됩니다. 장면 X로부터 local geometric context를 가져오기 위해 IF-Nets를 사용합니다. IF-Nets에서는 먼저 3D 복셀 데이터를 다중 CNN 다운 스케일 레이어를 통과시켜 다양한 해상도의 feature grid를 추출합니다. 다양하게 추출된 feature grid 에서 현재 포즈 근처에 해당하는 7개 지점의 픽셀의 값을 가져옵니다. 포즈는 다양하게 이동하고 기울어질 수 있기 때문에 당연히 feature grid와 정확하게 맞지 않을 가능성이 높은데요, 이 문제는 3차원 선형 보간을 통해 간단하게 해결됩니다. 각 feature gird에서 특징을 뽑아 이 모든 값들을 concat시킨게 ${^H}z$ 가 됩니다. 정리하면 아래와 같습니다.

\[p = [(0, 0, 0), (0, 0, d), (0, 0, -d), \space ..., (-d, 0, 0)]\] \[X: (64 \times 64 \times 64 \times \text{(feature dimension)})\] \[\underbrace {\begin{bmatrix} Z_1 \\ Z_2 \\ Z_3 \\ \vdots \\ Z_n \end{bmatrix} }_Z = \begin{bmatrix} \text{CNN}_1(X) \\ \text{CNN}_2(Z_1)\\ \text{CNN}_3(Z_2)\\ \vdots \\ \text{CNN}_{n}(Z_{n-1})\\ \end{bmatrix}\] \[{^H}z = (Z_1(Hp), Z_2(Hp), \space ..., Z_n(Hp)) \quad (n \times 7 \times \text{(num of CNN kernels)})\]

이렇게 얻은 local feature vector를 2개의 8층의 MLPs($ s_\theta$, $\mathcal G_\psi$)에 넣어 각각 스코어 예측과 샘플 자체 평가를 수행합니다. 스코어 네트워크는 스코어 점수가 필요하니까 넣어주는 것이고, 샘플 자체 평가는 이 샘플이 실제 유효 포즈에 가까운지 아니면 유효하지 않은 포즈이거나 노이즈에 가까운지 분류합니다. 이 분류를 바탕으로 낮은 평가를 받은 샘플을 버리거나, 우선순위에서 배제할 수 있습니다.

그리고 다양한 태스크에 대해 일반적으로 수행하기 위해, 태스크에 대한 정보를 제약으로 넣어줍니다. 제약으로 넣어주기 위해 두 MLP 네트워크의 사이사이에 FiLM구조의 Affine transformation 연산을 추가합니다. 이를 통해 모델은 다양한 태스크 제약에 따라 적절히 예측을 수행할 수 있습니다.

Sample-frame SE(3)-diffusion

이제 지역 좌표계에서 어떻게 역방향 diffusion이 수행되는지 알아봅니다.

\[v \sim \mathcal N(0, \sigma_k^2I)\] \[\tilde H = H \text{Exp}(v)\]

먼저, 6차원 실수 공간에서 랜덤 노이즈를 샘플링하고, 원래 포즈를 기준으로 동차 행렬 좌표계로 mapping 합니다. 이렇게 하면 원래 포즈 H에 대해, SE(3) 상의 노이즈를 적용한 것과 동일합니다. 노이즈가 더해진 동차 행렬을 얻었으면 위에서 설명한 네트워크를 통해 스코어를 구해줍니다.

\[\mathcal{L}_{\mathrm{DSM}} = \frac{1}{L} \sum_{k=0}^{L} \mathbb{E}_{H, \,\tilde{H} } \biggl[ \bigl\| s_{\theta}\bigl({^\tilde{H} }{z}, \sigma_{k}\bigr) \;-\; {^\tilde{H} }\nabla \,\log q_{\sigma_k}\bigl(\tilde{H} \mid H\bigr) \bigr\|_{2}^{2} \biggr]\]

위의 DSM(Denoising Score Matching) 손실함수를 통해 학습을 수행합니다. $q_{\sigma_k}$는 가우시안 분포일 뿐이어서 자동 미분을 통해 기울기를 구할 수 있습니다.

\[H_{k-1} = H_k \text{Exp}(\frac{\alpha_k}{2}s_\theta({^H}z, \sigma_k) + \sqrt{a_k}\epsilon), \quad \epsilon \sim \mathcal N(0, I)\]

스코어 함수로 위의 랭주뱅 동역학을 반복수행해 적절한 포즈로 조금씩 이동시킵니다.

Implementation Details

실험에 사용되는 모든 데이터들은 시뮬레이션을 통해 생성됩니다. 하나의 실험 환경에는 다양한 물체가 있을 수 있고, 데이터는 각 물체를 단위로 생성됩니다. Grasp Detection 태스크의 경우 antpodal sampling을 사용해 후보 타켓 포즈를 생성하고, Object Discription의 경우에는 수동으로 후보 포즈를 생성합니다. 이렇게 만들어진 후보 타겟들이 다 유효하지 않기 때문에 추가적인 검증을 수행합니다.

• Collision Detection: 그리퍼가 지면과 충돌하는지 확인합니다.
• Approach Axis: 그리퍼가 접근하는 방향이 z축과 이루는 각도가 90도 미만이어야 합니다. 그러니까 아래에서 위로 잡는 후보는 선택하지 않습니다.
• Grasp Visibility: 그리퍼가 잡을 위치까지의 거리와 센서 데이터상에 측정된 위치가 비슷한지 확인합니다(0.005 미만). 만약 두 거리 사이에 차이가 크다면, 포즈 접근 방법이 물체 내부를 통과하는 방향이거나, 잡으려는 위치가 센서상으로 관측되지 않는 영역임을 의미합니다.

위의 검증을 통과하지 못한 데이터들은 그냥 버리는게 아니라, 샘플 자체 평가 네트워크를 학습시키기 위해 사용됩니다.

입력 데이터로는 단일 가상 깊이 카메라로 얻은 point cloud map에서 가장 잘 대표될 수 있는 2000개의 점들로 downsampling 합니다. 0.005의 가우시안 노이즈가 추가되고, 이후 가로, 세로, 높이가 64(총 모서리의 길이는 0.3m)인 occupancy grid로 전환됩니다. 200개의 훈련 물체를 여러 스케일로 사용해, 총 30,000개의 훈련 장면을 생성해 사용합니다.

\[\mathcal{L}_{DSM} + 0.1\mathcal{L}_{focal}\]

총 5개의 CNN 레이어가 사용되었고, 입력, 출력, 첫 번째, 두 번째, 세 번째 히든 그리드가 사용됩니다. point kernel의 길이는 그리퍼의 크기에 맞춰 8cm로 설정되었습니다. 네트워크를 업데이트할 때 DSM 손실만 사용하게 되면 샘플 자체 평가 네트워크가 학습되지 않습니다. 따라서 이 네트워크를 학습시키기 위해 Focal 손실을 전체 손실에 작게 더해 업데이트합니다.

Experiment

크게 두 가지 실험이 수행되었습니다. 한 실험에서는 복잡한 환경에서 그립 포즈 생성 능력을 평가합니다. 다른 실험에서는 SPLIT 모델이 정말 다양한 태스크를 동시에 잘 수행할 수 있는지 평가합니다. 아래에서 차례대로 살펴봅니다.

Scene-based Grasp Generation Evaluation

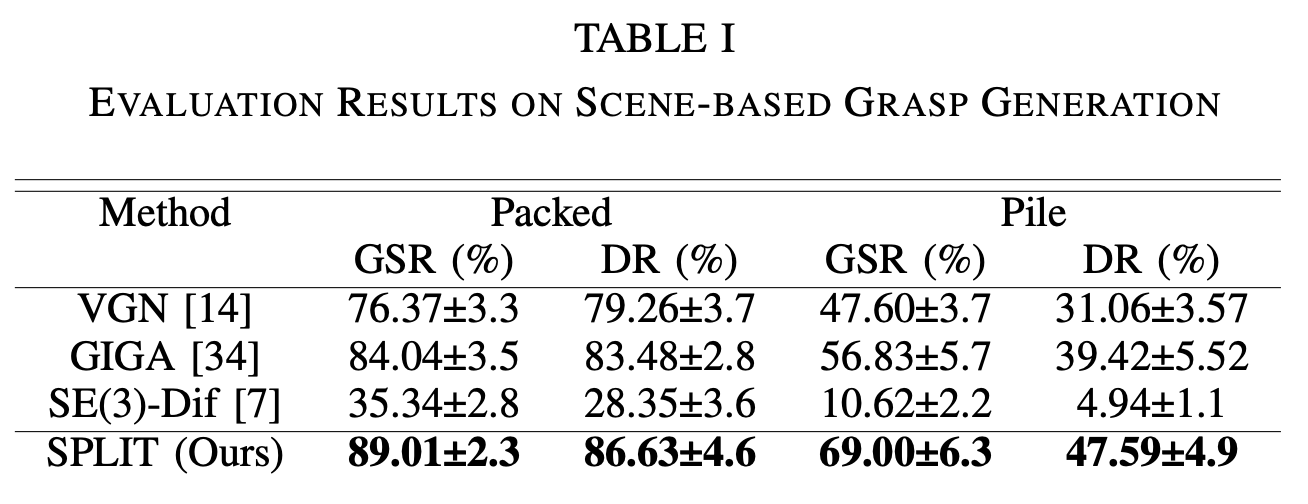
물체의 배치는 Packed 타입과 Piled 타입으로 구분됩니다. 에피소드는 아래의 조건이 만족될 때 종료됩니다.

• 모든 물체가 제거됨
• 더 이상 실행 가능한 그립 후보가 남지 않음
• 연속된 두 번의 그립 시도의 실패

위 테이블에서 GSR은 성공 횟수를 시도 횟수로 나눈 값을 의미하고, DR은 성공한 그립 횟수를 물체의 개수로 나눈 값을 의미합니다. 두 상황에서 SPLIT과 다른 모델을 함께 비교했을 때, 모든 경우에서 기존 방법들보다 높은 GSR과 DR 점수를 보여줍니다.

Multi-purpose Pose Generation for Mug Reorientation and Hanging Manipulation

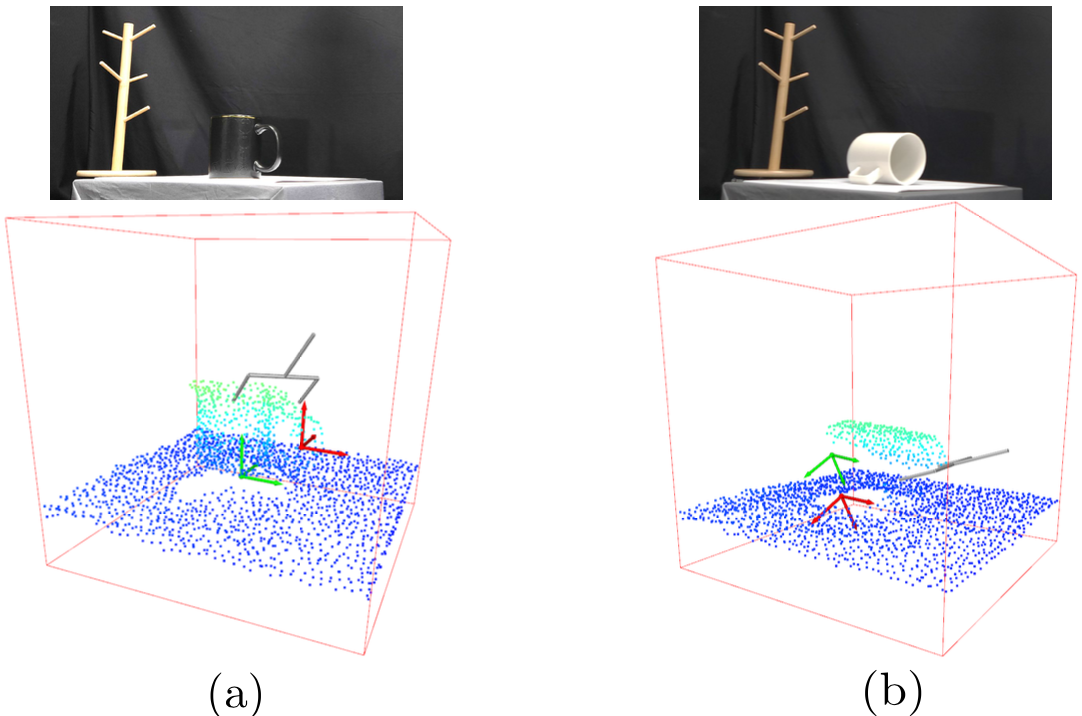
SPLIT 모델을 통해 다양한 태스크(그립, 핸들, 재배치)를 동시에 수행할 수 있는지 확인합니다. 구체적으로는 머그잔을 대상으로 재배치, 걸기 작업을 잘 수행하는지 실험합니다.

이 실험에서 목표하는 포즈는 아래와 같습니다.

• Graspable Pose: 잡을 수 있는 포즈
• Handle Pose: 손잡이를 잡기 위한 포즈
• Upright Placement Pose: 머그잔 재배치를 하기 위해 잡아야 하는 포즈

그런데 어떤 경우에서는 바로 걸기 작업을 수행하지 못할 수 있는데, 이 경우에는 머그잔을 바로세우고 다시 시도하게 됩니다. 머그잔이 완전히 뒤집힌 경우에는 잡을 수 있는 곳이 없기 때문에 제외합니다. 데이터를 수집할 때 모호성을 줄이기 위해 하나는 작업환경의 수직방향으로, 다른 하나는 45도 돌아간 상태에서 촬영합니다. ShapeNet에 있는 머그잔 물체로 학습을 수행하는데, 25개는 학습할 때 사용하고, 나머지 5개로는 실험에 사용합니다. 재배치와 걸기를 40회씩 수행시키고 개별 태스크에 대해 따로 성공률을 측정합니다.

전체 작업은 Ground Truth의 성공률이 77.5%인데, SPLIT의 작업 성공률은 70%로 90.3%의 상대 성공률을 보여줍니다. 재배치 태스크만을 따로 평가했을 때에는 92.5%의 높은 성공률은 보여줍니다.

Conclusion

SPLIT에서 제안하는 로컬 기하 정보를 활용한 포즈 추론 방식은, 기존의 전역 기준 좌표계 정보에 기반한 예측 방식에 비해 단일 태스크 추론 성능에서도, 일반화 성능 측면에서 훨씬 유리합니다. out-of-distribution 장면에서 SPLIT은 잘 동작하지 못하는 모습을 보이는데요, 이런 문제점은 더 큰 데이터셋으로 학습하거나, 도메인 랜덤화를 통해 해결할 수 있다고 주장합니다. 그리고 추가적인 피드백 시스템을 추가해 성공률을 더욱 높이는 것을 향후 연구 방향으로 제시합니다.