8 분 소요

이 포스팅은 ‘A Reachability Tree-Based Algorithm for Robot Task and Motion Planning‘에 대한 내용을 담고 있습니다.

논문 주소: https://arxiv.org/pdf/2303.03825

A Reachability Tree-Based Algorithm for Robot Task and Motion Planning

로봇이 계획부터 실제 수행까지 모든 조작 과정을 자율적으로 수행하게 만들기 위해 다양한 선행 연구들이 있어왔습니다. 로봇이 조작 과정 전체를 자율적으로 수행하기 위해서는 TP(Task Planning)과 MP(Motion Planning)을 수행할 수 있어야 합니다. 이 두 가지 계획을 모두 해결해야 하는 문제를 TAMP문제라고 합니다.Task Planning이란 태스크 수준에서의 계획 수립을 의미하고, Motion Planning은 그 각각의 개별 태스크를 수행하기 위한 구체적인 제어 계획(관절을 어떻게 움직여야 하는지)을 의미합니다. TP는 추상적인 수준에서 수립되기 때문에 실제 기하학적인 관계를 고려하기 어렵습니다. 주방에서 요리를 하는 예시를 들어보면, TP 단계에서 wash 이후 cook 라는 계획을 수립할 수 있습니다. 그런데 만약 세척을 수행해야는 싱크대와 조리를 수행해야 하는 스토브 사이에 이동을 어렵게 하는 장애물이 있는 경우에는 MP가 불가능할 수 있습니다. 대신에 중간에 거쳐갈 수 있는 도마가 있다면, wash을 하고 move to dish한 다음에 cook을 수행하는 경우에만 MP이 가능한 경우가 있을 수 있다는 거죠. 애당초 불가능한 태스크 계획에 대해 가능한 MP를 찾기 위해 많은 컴퓨팅 자원을 쓴 후에서야 불가능하다는 사실을 깨닫고, 다시 TP를 수행을 반복하는 과정은 불필요한 연산을 너무 많이 포함한다는 점에서 개선해야할 필요가 있습니다.

이러한 문제점을 해결하기 위해서 RRT(Rapid Exploring Reachability Tree)와 비슷한 방법을 사용하면서도, TP까지 수행할 수 있도록 하는 계층적 전략을 취하는 새로운 계획 모델을 제시합니다.

옮겨야 하는 물체가 존재하는 문제에서는 전형적인 MP로 해결하기가 어렵습니다. 이런 문제들을 해결하기 위해 모드(mode)라는 개념이 사용됩니다. 모드란 로봇이 충돌 없이 움직일 수 있는 자유 공간을 의미합니다. 물체를 옮길 때마다 로봇팔의 모드는 조금씩 변화하게 되는데요, 모드들 사이의 이동으로 계획을 수립하는 문제를 MMMP(Multi-Modal Motion Planning)이라고 합니다. 가장 잘 알려진 접근 방법은 RRT-like MMMP으로, 새로운 모드로의 이동을 트리의 간선으로 삼아 문제를 해결합니다. TAMP도 마찬가지로 조작 계획 문제를 다루는데, 여기서는 Symbolic Planner를 사용해 이산화된 상태 공간을 탐색합니다. TAMP의 경우 추상적인 상태와 행동에 대해 계획을 수립할 수 있다는 장점이 있습니다. 이 논문에서는 위의 모든 아이디어를 종합해 조작 계획 문제를 해결합니다.

Manipulation Planning Problem

TAMP 문제를 해결하기 위해 MP, MMMP, TP 방법론들을 모두 모아 다 같이 사용합니다. 각각의 아이디어들이 어떻게 사용되는지 아래에서 자세하게 살펴봅니다.

Problem Definition

\[(x_I, \mathcal{X}_G) \quad x_I \in \mathcal X(\text{initial state}) \quad \mathcal X_G: \text{set of goal states}\]

조작 계획 문제는 위와 같이 튜플로 정의할 수 있습니다. 하나로 결정된 시작 상태와, 목표 상태의 집합을 두 원소로 가지는 튜플로 정의됩니다. 이 문제에서 얻어야 하는 건, 어떻게 목표 상태 집합으로 이동할 수 있는지, 그 행동 나열을 찾아내는 것입니다. 목표 상태 집합은 특정 변수에 대한 수식으로 명세될 수 있습니다. 예를 들어 어떤 블록을 특정 위치에 이동시켜야 하는 태스크라면, 해당 블록이 x축으로 어떤 범위, y축으로 어떤 범위 안에 들어감을 표현하는 수식으로 목표가 표현될 수 있습니다.

Notation

다음으로 문제에서 사용하는 세부적인 표기법들에 대해서 살펴보겠습니다.

\[o :\text{object}\in \mathcal O \quad m :\text{movable object}\quad r:\text{robot}\] \[\mathcal M \subset \mathcal O \quad r \in \mathcal O\]

TP에서 object 집합은 movable object와 robot을 다 포함합니다.

\[\alpha_m = (m, p, {^m}T_P): \text{attachment}\] \[\text{where} \quad m \in \mathcal M, \space p \in \mathcal O, \space {^m}T_p \in SE(3)\]

위의 튜플을 attachment라고 합니다. attachment는 물체 사이의 접촉 관계를 표현하는데, 위의 표현은 m이 p 위에 붙어있음을 의미합니다. 그리고 가장 마지막 원소는 두 물체 사이의 변환 행렬이 됩니다. 그러니까 attachment는 두 물체 사이의 추상적인 관계(누가 누구한테 붙어있음)와 구체적인 위치 관계(변환 행렬)까지의 모든 정보를 포함합니다.

\[\sigma:\text{mode} = \{\alpha_m \mid m \in \mathcal M\} \in \Sigma :\text{infinite set of modes}\]

mode는 위와 같이 정의됩니다. 움직일 수 있는 모든 물체의 attachments를 원소로 하는 집합이 mode입니다. mode가 결정되면 로봇이 충돌 없이 움직일 수 있는 공간도 따라서 결정되는데 이를 $\mathcal C^\sigma_{free}$라고 표현합니다.

\[\tilde \alpha_m = (\text{attatched}\space\space\text{?m}\space\space\text{?p})\] \[\tilde \sigma = \{\tilde \alpha_m \mid m \in \mathcal M\}\] \[s = (\psi, \tilde \sigma)\]

attachment에서 포함하는 변환 행렬은 두 물체 사이의 관계를 정말 구체적으로 정확하게 결정하는데, TP를 수행할 때에는 이렇게까지 구체적인 정보를 결정하지 않습니다. TP는 object_1을 집음, object_1을 stove로 이동, … 이런 식의 굉장히 추상적인 수준에서 수행하고 구체적으로 어디에 놓을 지는 MP에서 결정합니다. 때문에 위와 같이 변환행렬을 제외한, 단순히 m이 p위에 붙어있다는 정보만을 포함하는 abstract attachment를 사용합니다. 그리고 모든 물체의 abstract attachment에 더해, non-geometric state까지를 원소로 갖는 튜플을 abstract state라고 합니다. non-geometric state란 기하적인 정보가 아닌 정보, 예를 들어 washed(object_1) = True와 같은 정보들을 의미합니다.

\[s' = T(s, a)\] \[a_g: \text{geometric action} \in \mathcal A \quad a_n: \text{Non-geometric action} \in \mathcal A\]

위의 abstract state 사이의 이동을 abstract action이라고 합니다. 그리고 이 abstract action을 특징에 따라 두 종류로 나누는데, 기하학적인 변화를 일으키는 행동을 geometric action(pick, place)이라고 하고, 기하학적인 변화를 일으키지 않는 행동을 Non-geometric action(wash, cook)이라고 합니다.

\[x \in \mathcal X = \Psi \times \Sigma \times \mathcal C\]

비기하학적인 논리 정보, 모드 공간, 그리고 로봇이 움직일 수 있는 공간의 Cartesian 곱으로 Hybrid state space가 정의되고, 이 공간 속에 존재하는 원소를 Hybrid state라고 부릅니다. 이 상태 표현은 시스템의 정확한 표현이 되긴 하지만, TP에서 필요한 abstract한 요소가 명시적으로 드러나지 않습니다. 우리는 지금 TAMP문제를 푸는게 목적이고, TP에서 추상적으로 계획을 수립해야 합니다. 따라서 조금 중복적인 표현이긴 하지만, Hybrid state를 아래와 같이 표현합니다.

\[x = (s, \sigma, q)\]

Hybrid state의 원소 중 Abstract state는 TP를 할 때 사용되고, MP를 할 때에는 시스템의 정확한 표현을 하기 위한 mode까지 함께 사용합니다. State transition은 위와 같이 정의된 Hybrid state들 사이의 이동으로 정의되는데, 어떤 원소가 바뀌어있는지에 따라 세 가지로 분류합니다.

  • Configuration transition: 관절각만 바뀐 경우
  • Mode transition: mode만 바뀐 경우. 예를 들어 싱크대에 담긴 물체를 로봇 팔로 집은 경우, 관절의 각도와 비기하적인 상태는 변화하지 않지만, 물체의 입장에서 싱크대 붙어있었다가 로봇 팔에 붙어있는 상태로 mode만 변하게 됩니다.
  • Non-geometric state transition: 비기하적인 상태만 변화한 경우

Our Planning Algorithm

이제 위에서 소개한 개념들을 가지고, 알고리즘이 어떻게 구성되는지 알아봅니다.

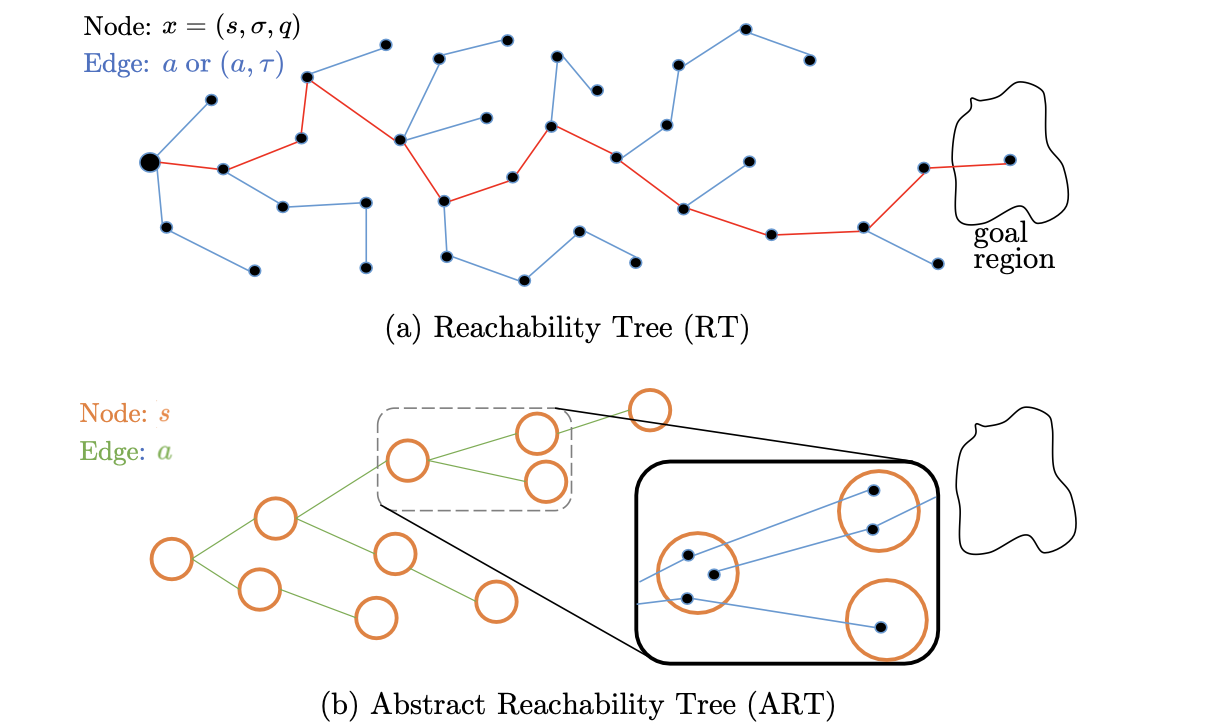
image-20250224221125496

일단 알고리즘의 목표를 명확히 하고 가야하는데, 우리의 목표는 목표 상태 집합에 속하는 상태로 이동하기 위한 경로를 찾아내는 것입니다. 그러니까 우리는 위의 그림에서는 RT를 계속 확장시켜 goal region에 속하는 state로 갈 수 있는 간선들의 집합을 찾아내야 합니다. 그런데 이걸 RT에서 무작정 바로 찾아내기는 어렵기 때문에 TP에서 추상적인 수준으로 계획을 수립합니다. 그리고 이 계획을 수립 하기 위해 위 그림의 하단에 위치한 ART(Abstract Reachability Tree)를 사용합니다.

ART는 추상적인 상태를 노드로 삼습니다. 그 추상적인 상태에 속하는 여러 RT상의 노드들이 있는데, ART에서 먼저 대략적인 계획을 수립하고 거기에 속하는 구체적인 RT 노드들을 결정하는 방식으로 알고리즘이 수행됩니다. 이런 일련의 과정들이 TAMP에서의 TP, MP와 대응되는데요, 구체적으로 이 논문에서는 TP layer, SS layer, MP layer라고 각 단계를 이름 짓고, 계층적으로 알고리즘을 수행합니다.

TP layer에서는 ART에서만 샘플링을 통해 행동 시퀀스를 뽑아냅니다. 샘플링 방법으로는 randomized tree search(MCTS 사용)으로 탐색을 한 다음, 탐색한 마지막 부분부터 symbolic planner를 사용해 목표까지의 Abstract 행동 시퀀스를 완성합니다. 다음으로 SS layer에서 TP layer의 출력으로 얻은 Abstract plan을 바탕으로 빠르게 attachment들을 먼저 샘플링해, 계획을 실행 가능성을 빠르게 판단합니다. 만약 실행이 불가능하다고 판단되면 TP layer로 다시 넘어가고, 실행이 가능하다고 판단되면 MP layer로 넘어가 RT에서 샘플링을 수행합니다.

Task Planning Layer

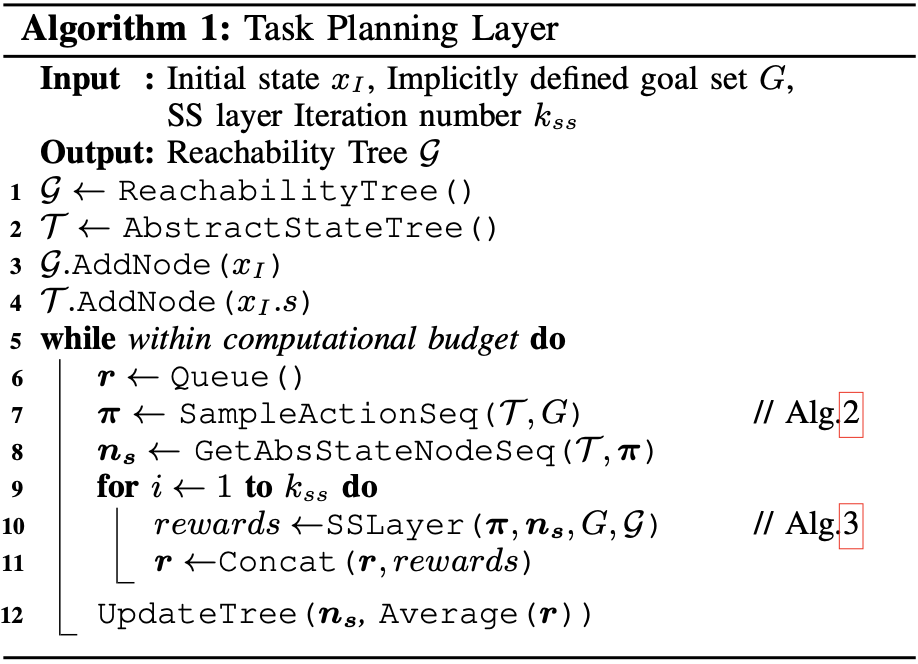
image-20250225093357804

위는 TP layer의 알고리즘 유사 코드입니다. 먼저 SampleActionSeq에서 MCTS와 Symbolic Planner를 통해 Goal까지 이동할 수 있는 ART 상의 경로를 빠르게 생성합니다. 그리고 그렇게 만들어진 Abstract plan에 대해 $k_{ss}$번 평가를 수행하면서 보상을 수집합니다. 그리고 그 보상들을 바탕으로 MCTS 를 업데이트해 다음에는 더 좋은 Abstract plan을 찾을 수 있도록 합니다.

  • SampleActionSeq

    image-20250225094557724

    ART에서 MCTS와 Planner를 사용해 경로를 찾아내는 알고리즘입니다.

Subgoal Sampling Layer

image-20250225095025979

SS layer에서는 TT layer에서 만들어낸 ART 경로를 가지고 RT에서 경로를 만들어 보면서 보상들을 수집합니다. 먼저, ART 경로를 받아 SampleBatchAttachments에서 abstract attachment가 아닌 attachment를 생성합니다.

  • SampleBatchAttachments

    image-20250225100044289

    attachment를 생성하는 알고리즘은 위와 같은데, abastract action을 역순으로 돌면서 만약 해당 행동이 goal에 직접적인 영향을 주는 행동이라면 G의 조건을 만족하도록 변환 행렬을 생성하고, 그렇지 않은 경우에는 일반적인 샘플링으로 변환 행렬을 생성해 attachment를 완성합니다.

MakeGoalCandidate는 생성된 attachment를 통해 마지막 Hybrid state를 만듭니다. 이 마지막 Hybrid state에 collision이 존재하면, collision이 없는 Hybrid State를 찾기 위해 다시 새로운 attachment를 생성하는 과정을 $k_{goal}$ 횟수만큼 수행합니다. 이 횟수동안 collision이 없는 경우를 찾지 못하면 아무런 보상을 받지 못한 채로 알고리즘이 종료되고, 만약 collision이 없는 경우를 찾았다면, 반복문을 즉시 탈출해 RT를 탐색하는 단계로 넘어갑니다.

일단은 가장 처음 행동에 해당하는 상태부터 탐색을 시작합니다. ART의 첫 스텝 상태와 대응하는 RT와의 포인터는 주어진 상태로 시작합니다(시작 상태는 명확하게 주어지기 때문). 현재 상태의 행동이 non-geometric action이라면, non-geometric transition만 해주면 되는데 그 과정에서 motion planning을 할 필요는 없으므로 바로 다음 Hybrid state를 찾아줄 수 있습니다. 반면에 Geometric action인 경우, 각도에 해당하는 q가 변하게 되는데 이 값은 충돌을 일으키지 않도록 샘플링됩니다. 아무튼 다음 Hybrid state를 찾았다면, 두 state 사이의 motion planning을 수행합니다. motion planning에 성공한 경우 찾은 다음 Hybrid state의 포인터를 추가해 트리를 확장합니다. 만약 성공하지 못했다면, 해당 행동의 스텝수에 비례하는 양 만큼의 보상을 저장합니다.

그러니까 RT 상에서 상태노드들은 계속 순차적으로 확장되는데요, 가장 마지막 상태에서의 확장이 성공적으로 수행되었다면, 목표 상태로 도달할 수 있는 완전한 경로를 찾아낸 것이 됩니다.

Empirical Evaluation

실험은 TAMP 벤치마크 문제로 사용되는 3가지 상황에서 수행되었습니다.

  • Kitchen m domain

    image-20250225115100037

    m개의 식품 블록과 3개의 배치 가능한 장소(sink, stove, dish)로 구성됩니다. 음식 블록은 cooked 이전에 washed 되어야 하고, 이를 위한 non-geometric actions인 cook과 wash가 있습니다. 위 그림에서 볼 수 있듯, 장소의 크기가 굉장히 좁기 때문에 블록을 밀집해 배치시켜야 합니다.

  • Non-monotic m domain

    image-20250225115211434

    서로 다른 색의 블록들과 발판, 그리고 키가 큰 블록이 각 블록 앞에 위치합니다. 키가 큰 블록이 색상 블록을 집는 것을 방해하기 때문에, 키가 큰 블록들을 제거하는 것이 전체 태스크 수행 과정 중에 중요한 과제가 됩니다

  • The blocktower m domain

    image-20250225115445071

    m개의 블록과 배치 가능한 발판들이 있습니다. 처음에 양 쪽에 블록들이 무작위로 쌓여있는 상태로 시작합니다. 이 태스크의 목표는 가운데 발판에 특정 순서로 블록들을 쌓는 것 입니다. 이를 위해서 stack과 unstack이라는 두 개의 abstract action이 사용됩니다.

비교 대상으로는 현재 널리 사용되는 TAMP 솔버인 PDDLStream을 사용합니다. 그리고 SS에서 attachment로 빠르게 feasibility를 체크하는 부분과 MCTS에서 보상 신호를 활용하는 두 가지 기능이 정말 도움이 되는지 확인하기 위해, 이들을 제거했을 때의 성능을 같이 제시합니다.

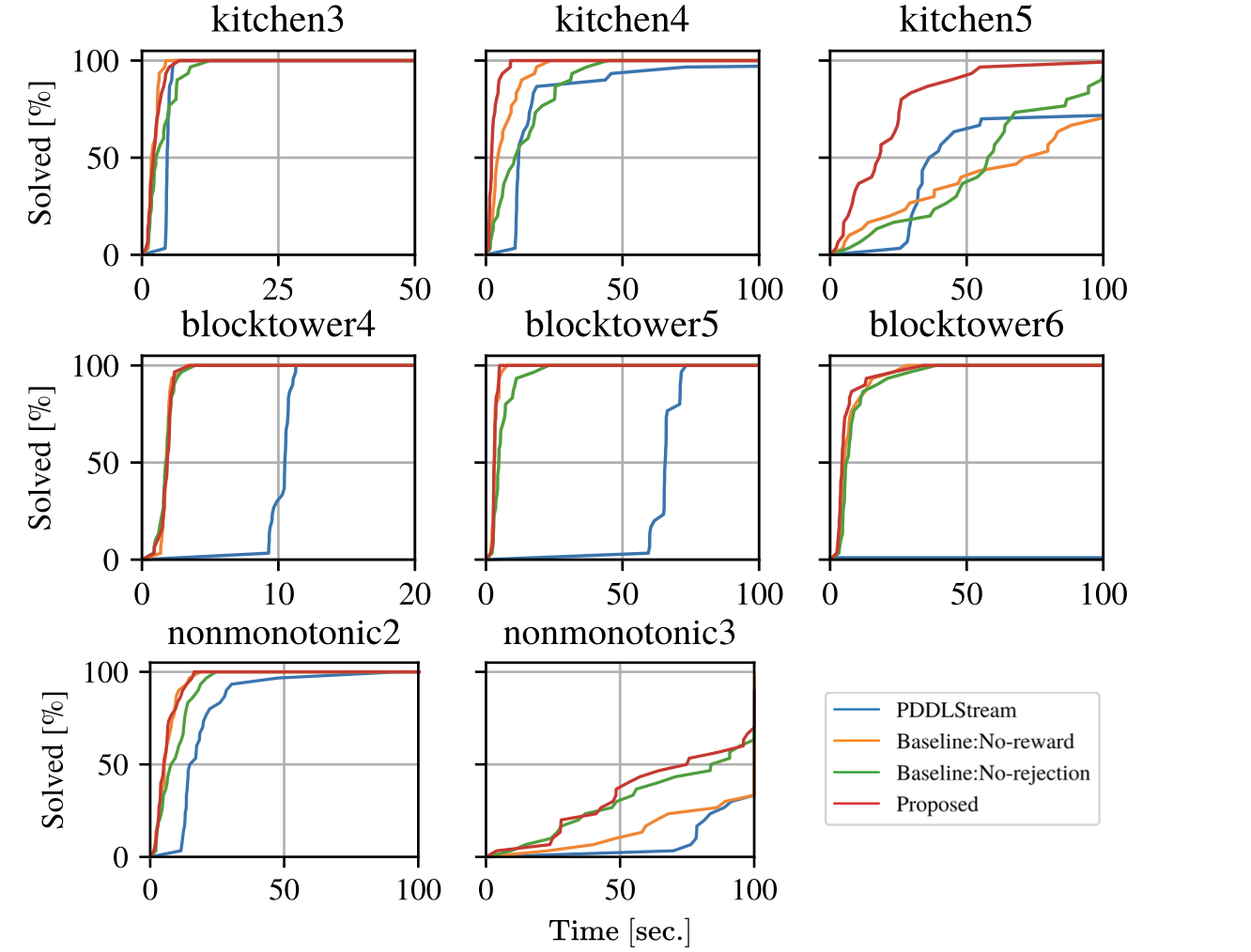
image-20250225115857719

kitchen 환경에서 숫자 높아질수록 더 복잡한 환경인데, 가장 복잡한 환경에서는 제안한 모델의 성능이 가장 높게 나타납니다. 환경이 복잡할수록 TP의 중요도가 높아지기 때문인 것으로 보입니다. 단순한 환경의 경우 보상을 사용하지 않는 경우가 더 좋은 성능을 보이기도 했는데요, 이는 간단한 환경이면 무작위로 TP를 만든다고 해도 feasible할 확률이 높기 때문인 것으로 생각됩니다.

non-monotonic 환경에서는 PPDLStream과 비교했을 때 훨씬 더 빠르게 수렴하는 결과를 확인할 수 있습니다. 그리고 이 환경에서는 두 기능을 제거했을 때에 큰 차이가 나타나지 않았습니다.

blocktower 환경에서는 각 기능을 제거했을 때에도 PPDLStream보다 더 우수한 성능을 보여줍니다. 제안된 방법에서는 TP와 MP를 분리하고, TP에서는 추상적인 수준에서 계획을 수립하기 때문에 블록이 많은 경우에 있어서도 훨씬 더 안정적으로 학습할 수 있습니다.

Conclusion

이 논문은 MMMP 아이디어를 사용한 새로운 RRT 기반 TAMP 솔버를 제안합니다. 이 알고리즘에서는 목표 후보를 사전에 생성해 샘플링 거부를 하는 기능을 추가함으로써 탐색을 보다 효율적으로 수행할 수 있습니다.

댓글남기기

참고

Isaac Lab 강화학습

16 분 소요

이 포스팅은 ‘Isaac Lab‘에 대한 내용을 담고 있습니다.