Learning-based Initialization of Trajactory Optimization for Path-following Problems of Redundant Manipulators

이 포스팅은 ‘Learning-based Initialization of Trajactory Optimization for Path-following Problems of Redundant Manipulators‘에 대한 내용을 담고 있습니다.

논문 주소: https://ieeexplore.ieee.org/document/10161426

Learning-based Initialization of Trajactory Optimization for Path-following Problems of Redundant Manipulators

이 논문에서는 로봇 매니퓰레이터의 말단부를 제어하는 Path-Following 문제를 다룹니다. 말단부가 특정 경로를 따라가게 하기 위해서는 그에 맞는 관절 궤적이 필요한데, 이 때 아무런 관절 궤적을 선택하는 것이 아니라 로봇의 관절 한계를 넘어서지 않는지, 특이점을 지나는 경로인지, 주변에 존재하는 물체와 충돌하는지 등등 고려해야할 대상이 많습니다. 그리고 그 중에서도 가장 적절한 관절 궤적을 찾아내는 것은 꽤 까다로운 일입니다.

가장 전통적으로는 differential IK를 사용해 국소 해를 찾는 방법이 있습니다. 이 방법은 너무 근시안적인 측면이 있고, 또, 특이점 주변에서 잘 동작하지 않는다는 문제점이 있었습니다. 다른 방법으로는 전역 탐색을 통해 최적해를 찾는 방법도 있는데, 이 방법은 너무 시간이 많이 걸린다는 단점이 있습니다. 최근에는 TO(Trajectory Optimization) 방법론이 가장 잘 사용되는데, 이 방법에서는 경로를 추종하도록 하는 목적함수를 설정하고, 최적화를 통해 초기 경로에서 점점 요구되는 경로에 맞아지도록 조금씩 업데이트됩니다. 근데 당연히 관절 궤적을 찾는 문제는 non-convex하기 때문에 초기 경로에 따라 다른 수렴 값을 가지게 됩니다. 그렇기 때문에 TO는 초기 관절 궤적이 굉장히 중요합니다.

관절 궤적 상에서 선형으로 초기 궤적을 설정하는 방법도 있고, 역기구학 해를 greedy하게 선택해 초기 궤적을 설정하는 방법도 있습니다. 이 논문에서는 강화학습을 기반으로 하는 RT-ITG를 통해 초기 궤적을 만들어내 이전의 방법론들보다 비교했을 때 훨씬 더 좋은 성능을 보여줍니다.

Problem Definition and Motivation

\[X = [x_0, x_1, x_2, ..., x_{N-1}] \in \mathcal X\] \[\xi = [q_0, q_1, ..., q_{N-1}] \in \Xi\]

말단부의 궤적과, 관절 궤적을 위와 같이 표현할 수 있습니다. 관절 변수의 차원은 사용하는 로봇의 자유도로 설정됩니다. 이 논문에서는 7자유도 Fetch 로봇을 사용해서 7을 설정됩니다.

\[\mathcal U[\xi] =\mathcal U_{\text{pose}}[\xi] + \lambda_1\,\mathcal U_{\text{obs}}[\xi] + \lambda_2\, \mathcal U_{\text{smooth}}[\xi]\]

TO의 목적 함수는 위와 같이, 말단부의 포즈가 요구되는 궤적과 일치하는지, 주변 환경과 충돌하는지, 그리고 마지막으로 로봇의 행동이 부드러운지에 대한 평가치를 모두 합산합니다.

RL-based Initial Trajectory Generator

RL-ITG는 초기 경로를 강화학습 에이전트의 일련의 행동들을 통해 생성합니다. 문제를 어떻게 정의되고 목적함수는 또 어떻게 설정되는지 살펴봅니다.

Formulation of an MDP and an RL objective function

\[\mathcal M_X = \langle \mathcal S, \mathcal A, \mathcal R_\mathcal I, \mathcal T, \mathcal Q_0, \gamma \rangle_{X \sim \mathcal X}\] \[\mathcal R_\mathcal I : = \text{time varying reward function}\] \[\mathcal I = \{ i \in \mathbb N | 0 \leq i \lt N\}: \text{time steps}\]

MDP 문제 정의는 위와 같이 설정됩니다. 가장 처음에 시작하는 포즈는, 역기구학 해 중에서 샘플링을 통해 결정합니다.

\[\text{maximize}_\pi \; \mathbb{E}_{X \sim P(X)} \left[ \mathbb{E}_{(s_i,a_i) \sim \rho_\pi,\; q_0 \sim Q_0} \left[ \sum_{i=0}^{N-1} \gamma^i \cdot R_i(s_i, a_i) \right] \right]\]

목적함수는 다른 강화학습 문제와 동일한 형식으로 설정됩니다.

\[s_i = (q_i, p_i^\text{link}, p_i^\text{target}, z_{env})\] \[p_i^\text{link} \in \mathbb R^{(d + 1, 9)}\]

상태는 위와 같이 현재 관절 각도, 링크별 위치 및 방위, 현재 말단부 위치와 이 다음 K개 목표 말단 위치 사이의 상대적 거리, 마지막으로 3차원 occupancy grid map과 같은 인지 정보의 임베딩 벡터로 구성됩니다.

\[a_i = \Delta q_i \in \mathbb R^d\] \[q_{i+1} = q_i + \Delta q_i\]

action은 관절 공간의 벡터로 얻게되고, 이 값을 현재 관절각도에 더해 다음 상태로 이동하게 됩니다.

Reward Function

이어서 보상함수가 어떻게 설정되는지 살펴봅니다.

\[e^\text{pos}_{ i} = \| x^\text{pos}_{ i} - \hat{x}^\text{pos}_{ i}(q_i) \|_2\] \[e^\text{pos}_{ i} = 2 \cdot \cos^{-1}\Bigl( \Bigl| \langle x^\text{quat}_{ i},\, \hat{x}^\text{quat}_{ i}(q_i) \rangle \Bigr| \Bigr)\] \[\langle \cdot \rangle: \text{inner product}\]

먼저 말단부의 위치와 방위에 대해 각각 거리 오차를 구합니다.

\[f(e, w) = w_0 \cdot \exp(-w_1 \cdot e) - w_2 \cdot e^2,\quad f(e,w) \in \mathbb{R}\] \[R_{\text{task}, i} = f(e^\text{pos}_{ i}, w^\text{pos}) + f(e^\text{rot}_{ i}, w^\text{rot}) \cdot \mathbf{1}_{\sqrt{e^\text{pos}_{ i}} \leq 5\,\text{cm}}\]

위치 방위에 대한 오차를 그냥 합으로 사용하기 보다는, 각각에 대해 가중치를 부여하는 정규화 함수를 시켜 얻은 결과값의 합을 사용합니다. 그런데 방위에 대한 오차는 처음부터 바로 사용하지 않고, 일단 거리 오차를 먼저 줄이게 하기 위해서 거리 오차가 5cm 이하로 줄어든 경우에만 방위 오차를 사용하도록 합니다.

\[e_{\text{im}, i} = \Bigl\| \Bigl( I - J(q_i)^\dagger J(q_i) \Bigr) \Bigl( \xi_{\text{demo}}[i] - q_i \Bigr) \Bigr\|_2\] \[R_{\text{im}, i} = f(e^\text{im}_{ i}, w^\text{im})\]

다음으로 에이전트가 전문가 TO 방법론의 Null-space상의 행동을 모사하도록 하기 위해서 SDF를 기반으로 한 전문가 TO 방법론으로 얻은 데모 관절 궤적 경로와의 거리 보상에 반영합니다. 그런데 두 관절 궤적의 차이를 그대로 반영하면 강화학습 에이전트가 전문가 TO 방법론의 데모 경로를 그대로 따르게 되는데, 이렇게 학습시키면, 에이전트가 전문가 TO 방법론이 만들어내는 데모 경로를 완전히 따라 만들게 될 뿐, 그보다 더 좋은 경로를 생성하지 못합니다. 여기에서 학습시키고자 하는 것은 제약 조건 내에서 부드럽고 일관된 Null-space 모션이므로, 단위행렬에 자코비안과 자코비안의 무어-펜로즈 역행렬을 행렬곱한 값을 빼 얻은 행렬을 곱해 Null-space에 투영합니다. 이렇게 얻은 거리를 마찬가지로 정규화 함수를 통과시켜 얻는 출력 값을 보상으로 사용합니다.

\[R_{\text{cstr}, i} = R_{C, i} + R_{J, i} + R_{S, i} + R_{E, i}\] \[R_{C, i} = -10 \cdot \mathbf{1}_{\text{collision}}\] \[R_{J, i} = -1 \cdot \mathbf{1}_{q_i < q_{\min} \text{ or } q_i > q_{\max}}\] \[R_{S, i} = -0.1 \cdot \mathbf{1}_{\det\bigl(J(q_i)J(q_i)^T\bigr) < 0.005}\] \[R_{E, i} = -3 \cdot \mathbf{1}_{\sqrt{e_{\text{pos}, i}} > 20\,\text{cm}}\]

마지막으로 충돌, 관절 한계, 특이점 등의 물리적 제약 조건에 대한 보상을 위와 같이 설정합니다. 충돌 시 -10의 벌점, 관절 한계를 넘어갈 시 -1의 벌점, 행렬값이 0.005 미만으로 내려가 특이점 발생 확률이 높아지면 -0.1의 벌점, 그리고 목표 위치에서 20cm 이상 멀어지면 -3의 벌점을 부과하고 에피소드를 조기 종료시킵니다.

\[R_i = R_{\text{task}, i} + R_{\text{im}, i} + R_{\text{cstr}, i}\]

위의 모든 보상들을 모두 더해 얻은 최종 보상으로 에이전트를 학습시킵니다.

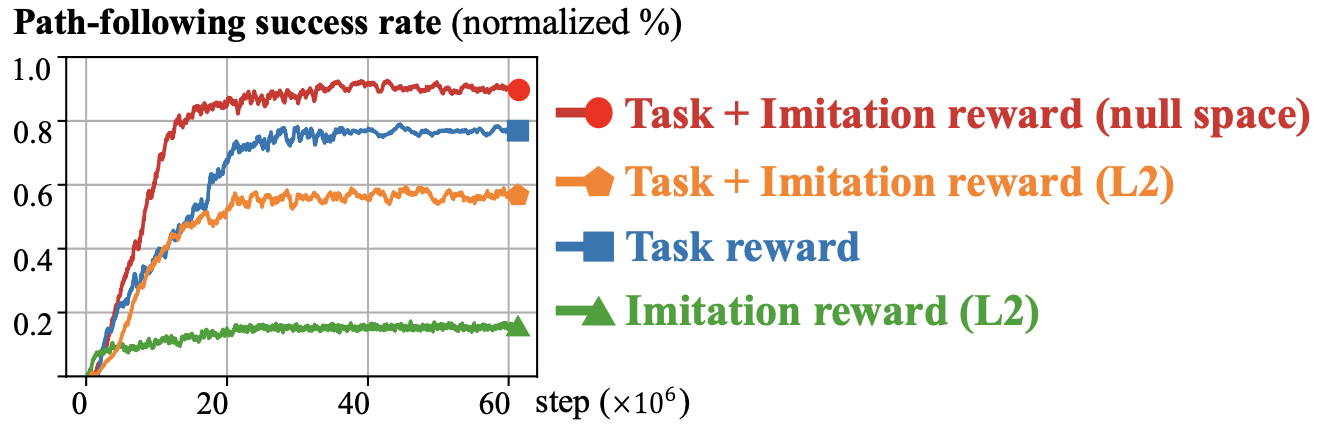
위 그래프는 보상들을 어떻게 조합하는지에 따른 일종의 Ablation study 인데, 논문에서 제안한 조합으로 보상을 정의했을 때 가장 높은 성능을 보여줬습니다.

Generation of Training Environments and Examples

에이전트가 다양한 상황들에서 적용될 수 있도록 하기 위해 다양한 path-following 문제를 만들어 사용합니다. x축으로 [0.2, 1.2], y축으로 [-0.7, 0.7], 그리고 z축으로 [0.0, 1.2]의 범위에서 충돌을 일으키지 않는 5,000개의 지점을 샘플링합니다. 그 5,000개의 지점들 중 5개에서 8개 지점을 랜덤으로 샘플링하고, B-스플라인과 spherical linear interpolation을 사용해 점들 사이의 위치와 방위를 보간해 총 5,000개의 경로를 수집합니다. 동일한 방법으로 장애물이 있는 환경에서 경로를 수집합니다. 테이블 위에 장애물을 무작위로 배치해 500개의 scene을 생성합니다. 그리고 각 scene에서 20개의 경로를 생성해 총 10,000개의 경로를 생성합니다. 따라서 총 15,000개의 경로를 가지게 되고, 시작 지점의 자세에 대한 역기구학 해 중 2개를 무작위로 샘플링하기 때문에 결론적으로 30,000개의 문제가 생성됩니다. 그리고 각 문제에 대해 TORM이라는 expert TO method를 사용해 데모 궤적을 준비해둡니다.

Training Details

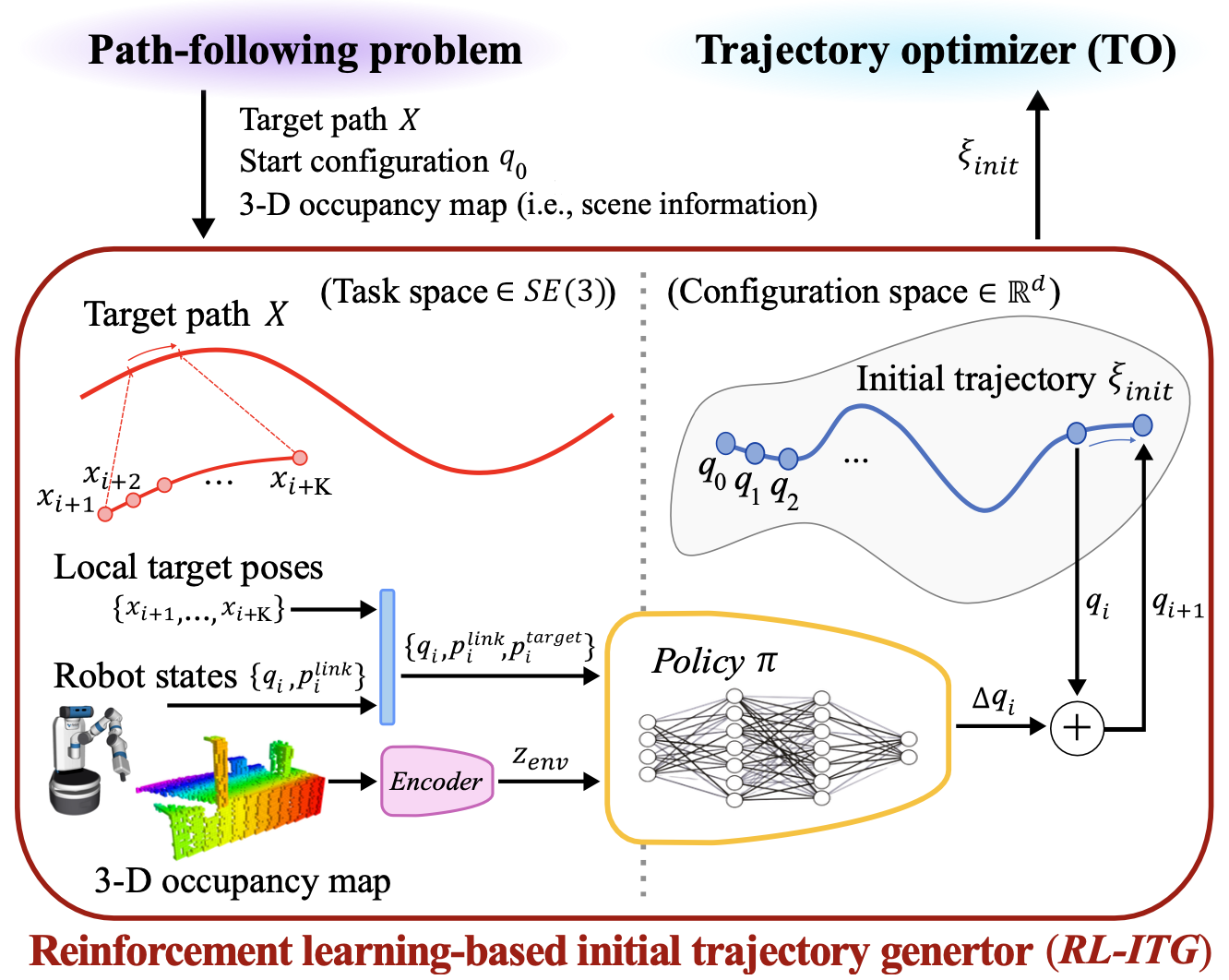
정책 학습에는 SAC(Soft Actor Critic)이 사용됩니다. 그리고 정책 네트워크와 Double Q-Network는 모두 1,024개의 뉴런 구성된 3장의 fully-connected 레이어로 구성됩니다.

\[\pi_\theta(a|s) \sim 0.26 \cdot \tanh(N(\mu_\theta(s), \Sigma_\theta(s)))\]

정책은 위와 같이 가우시안 분포로 모델링되고, tanget hyperbolic 함수에 0.26을 곱해 출력을 제한합니다. 이렇게 출력을 제한해서 궤적이 부드럽고 자연스럽게 이어지도록 만들어줍니다. 총 30,000,000번의 시뮬레이션 스텝을 통해 정책 학습이 수행되며, Intel i9-9900K, RTX 2080 TI 에서 144시간 동안 학습되었습니다.

RGB-D 카메라로 얻은 3차원 occupancy map은 VAE(Variational AutoEncoder)를 통해 32차원 벡터로 압축되어 사용됩니다.

Experiments

비교 베이스라인으로 단순 선형 보간법과 greedy 방법, 그리고 전문가 데모를 동일하게 모방하도록 학습시킨 BC-ITG를 사용합니다. TO 알고리즘으로는 TORM과 TrajOpt를 사용해 논문의 초기화 방식이 각 알고리즘에 어느정도의 효과를 주는지 평가합니다.

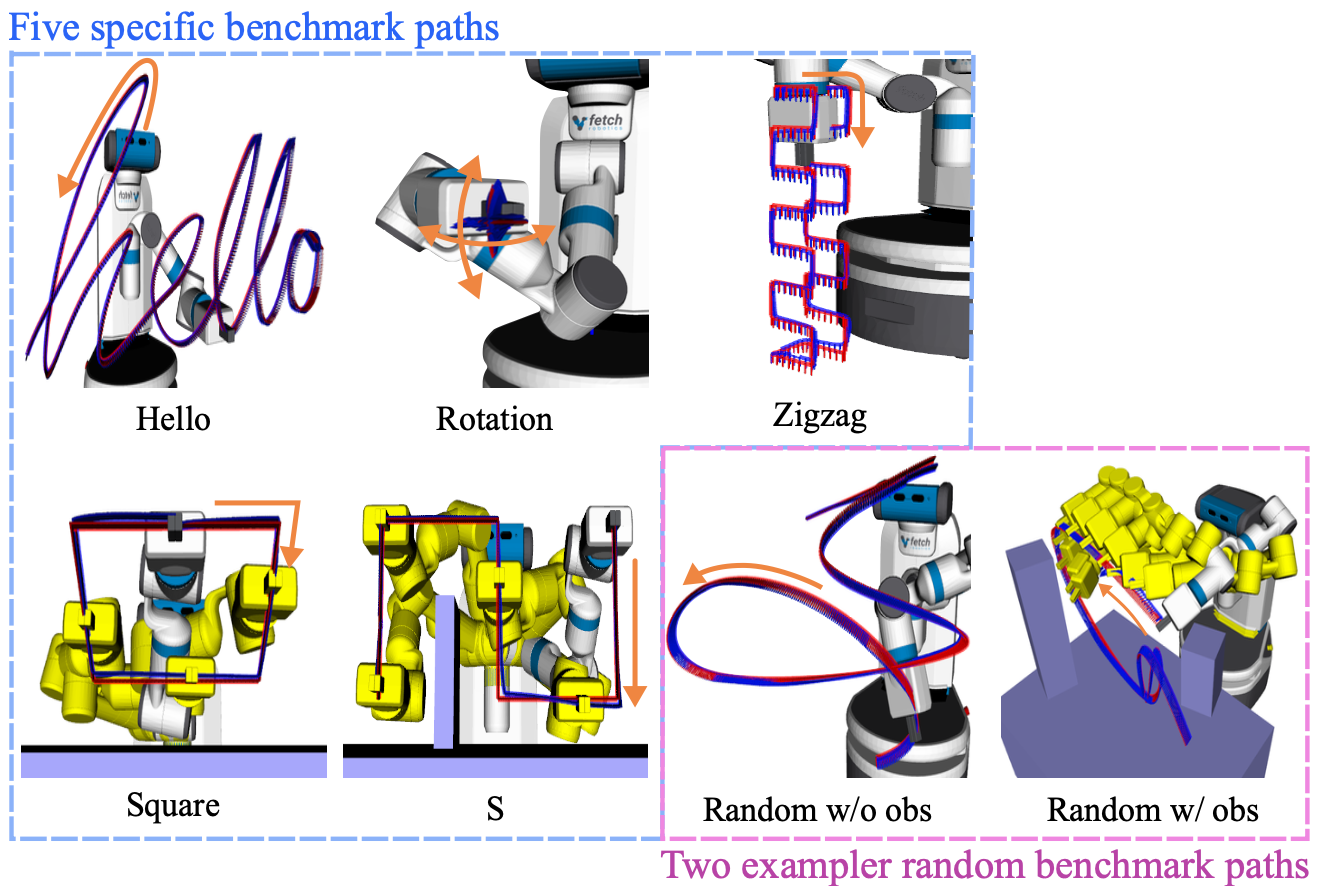
테스트 벤치마크로 위의 5가지 ‘Specific’ 경로를 사용합니다. ‘Rotation’의 경우 고정된 위치에서 방위가 움직입니다. 이를 제외한 나머지 네 경로들에서는 방위가 고정되고, 위치를 움직입니다.

추가로 ‘Random’ 벤치마크라는 것을 만들어 평가에 사용하는데요, 경로 생성 절차는 훈련 데이터셋을 만들 때와 동일합니다. 외부 장애물이 없는 100개의 경로와 장애물이 있는 1,000개의 경로를 수집합니다.

각 경로에 대해 ‘Specific’의 경우 100개의 초기 관절값을 샘플링하고 ‘Random’은 5개의 초기 관절값을 샘플링합니다. ‘Specific’에서 500개, ‘Random’에서 5,500개를 얻게 되므로 총 6,000개의 초기 경로를 획득하게 됩니다.

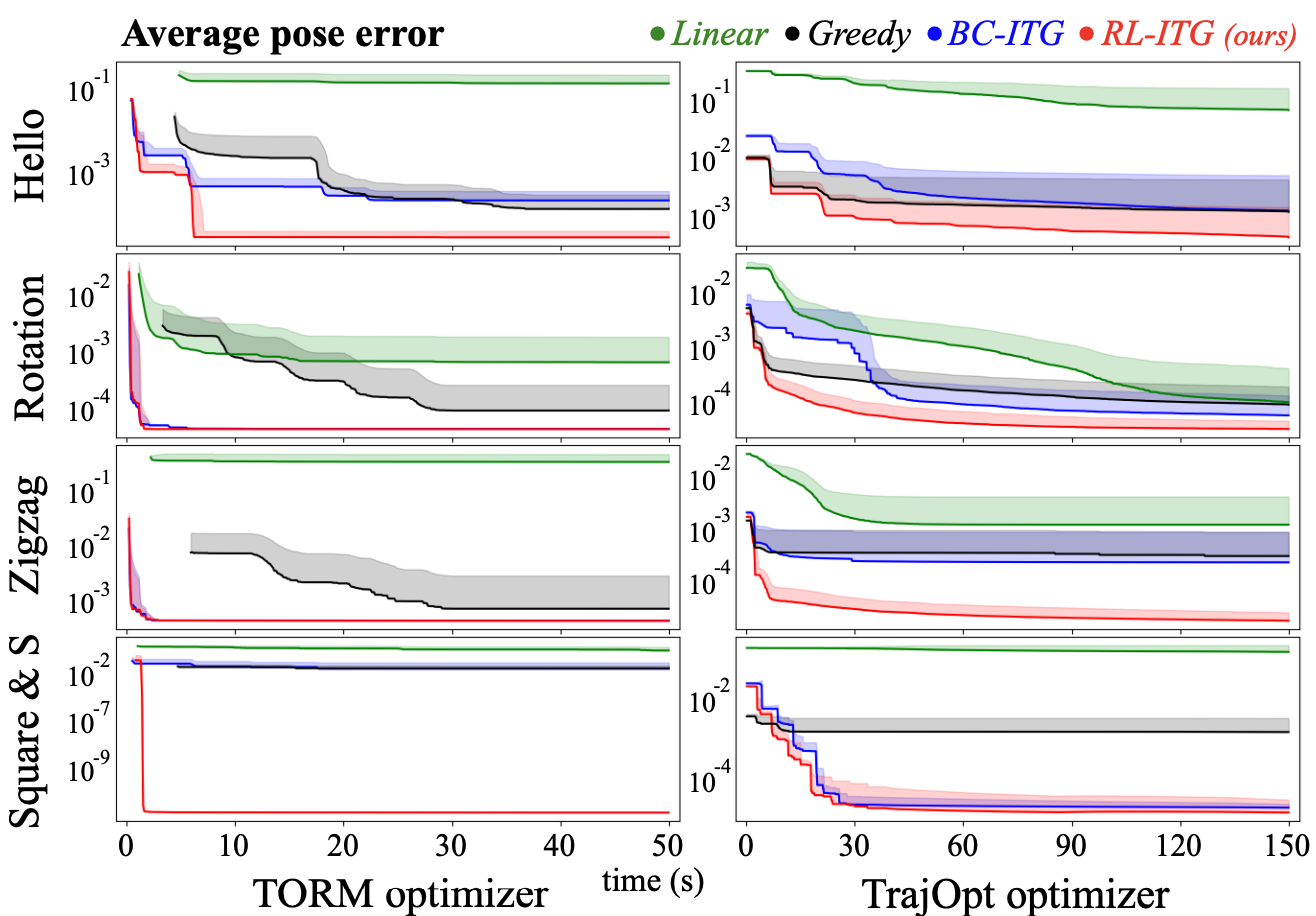
위는 Specific 벤치마크에서 베이스라인과 두 가지 TO 방법론이 성능에 미치는 영향을 평가한 실험 결과입니다. 모든 경우에서 RT-ITG가 가장 낮은 오차 수준에 도달함을 확인할 수 있었고, 수렴 속도도 평균적으로 가장 빠르게 나타납니다.

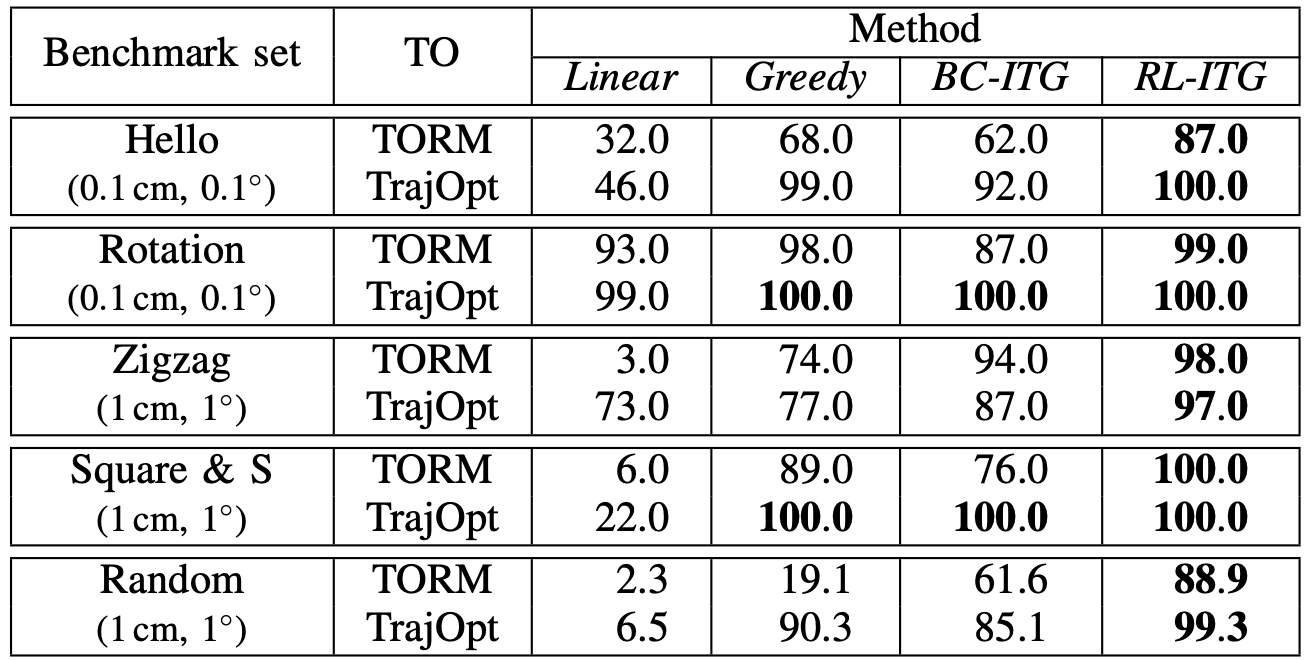
최종적인 성공률에서도 RL-ITG가 가장 높은 점수를 보여줍니다. 특히 Random 벤치마크에서 Linear와 Greedy 방법과 비교했을 때 큰 성능 차이를 보여줍니다.

위는 각 방법론으로 생성한 초기 궤적으로 도달하는 최종 비용함수값, 제약 위반 비율, 그리고 초기 궤적이 생성되는 시간을 보여줍니다. RT-ITG로 생성한 경로가 위 세가지에서 부문에서, 모든 경로에 있어서 좋은 결과를 보여줍니다.

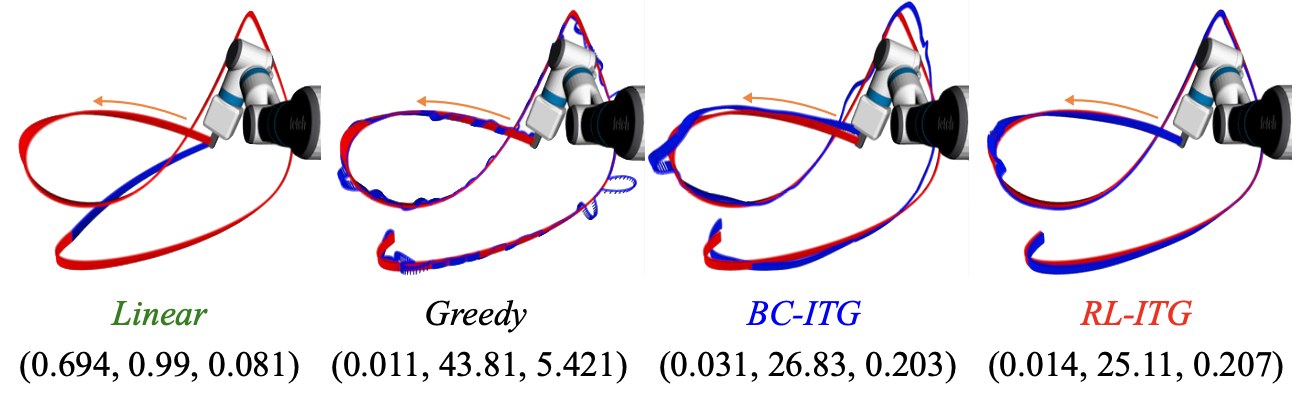
초기 궤적을 보면 RL-ITG로 만든 궤적이 다른 방법론으로 만든 궤적과 비교했을 때 부드럽다는 것을 확실하게 관찰할 수 있습니다.

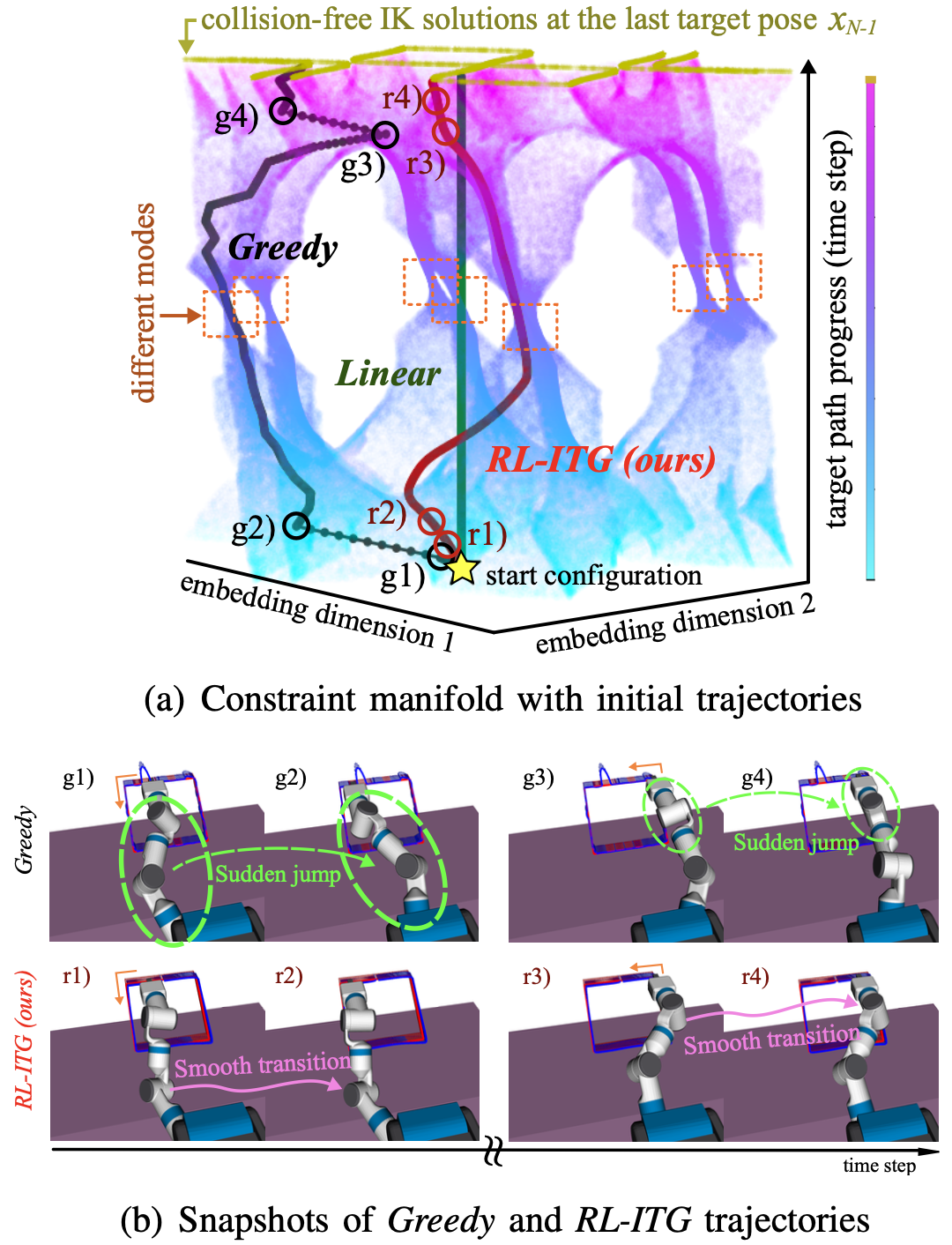
위는 Greedy 방식과 RL-ITG의 방식으로 만들어진 두 궤적의 전체적인 스냅샷을 보여줍니다. Greedy한 방식으로 생성된 경로는 특정 구간에서 급격하게 포즈가 바뀌는 구간이 있는 반면, RL-ITG 방식으로 만들어진 경로에서는 일관되게 부드러운 경로로 이어지는 것을 확인할 수 있습니다.

Conclusion

RL-ITG는 TO에서 더 나은 초기값을 찾는 방법론으로 실험을 통해 기존 베이스라인 방법론들과 비교했을 때 훨씬 더 나은 성능을 보여줍니다. 향후 연구 방향으로 더 다양한 scene에서 적용될 수 있게 하고, receding horizon control scheme과 결합해 동적인 환경, 그리고 time-varing 목표 경로에 대해서도 사용할 수 있도록 하는 발전시키는 방향을 제시합니다.