Online Multi-Contact Feedback Model Predictive Control for Interactivate Robotic Tasks

이 포스팅은 ‘Online Multi-Contact Feedback Model Predictive Control for Interactivate Robotic Tasks‘에 대한 내용을 담고 있습니다.

논문 주소: https://arxiv.org/pdf/2403.08302

Online Multi-Contact Feedback Model Predictive Control for Interactivate Robotic Tasks

과거와 달리 인간과 로봇이 동일한 작업 공간을 공유하는 경우가 있고, 그렇게 설계된 로봇들도 많이 나오고 있습니다. 인간과 작업공간을 공유하는 경우, 당연하게도 돌발요소가 더 많이 존재합니다. 예를 들어 사람이 지나가다가 로봇 팔을 툭, 쳐서 외력을 전달하게 되면, 전체적인 계획이 틀어져서 기존에 수립했던 계획을 성공적으로 완수할 수 없게 됩니다. 때문에 작업환경에서 돌발적으로 발생할 수 있는 여러 물리적인 상호작용을 포착하는 능력은 태스크를 수행할 때에 반드시 필요합니다. 예를 들어 테이블 연마를 하는 작업에서는 테이블에 힘을 줌과 동시에 위치를 움직여야 합니다. 이렇게 두 가지 작업을 동시에 수행하도록 하는 것은 꽤나 까다로운 작업인데, 이런 종류의 태스크를 Hybrid Motion-Force Control이라고 합니다.

요즘에는 컴퓨팅 속도가 크게 발전해 최적화를 활용한 문제 해결 방법이 많이 사용됩니다. MPC(Model Predictive Control)가 그 대표적인 방법입니다. MPC를 사용하기 위해서는 로봇과 환경의 접촉 모델에 대한 명시적인 설정이 필요합니다. 외력이 어떤 식으로 팔에 작용하는 지가 정확하게 알고, 또 그 힘을 이겨내는 방향으로 로봇의 관절 토크를 조절하기 위해서는 모델이 완전하게 명세되어야 합니다. 기존의 방법론들에서는 단일 접촉에 대해서, 그것도 end effector에서 발생한 접촉에 대해서만 다룰 수 있습니다. 당연히 현실에서는 여러 군데에서 접촉이 동시에 발생할 수도 있고 end effector가 아닌 다른 부분에서도 접촉이 발생할 수 있는데, 이런 상황들은 기존 방법론으로 해결할 수 없습니다.

이 논문에서는 MCP-EP(Multi-Contact Particle Fileter with Exploratiobn Particle)이라는 기존 알고리즘을 사용해 다중 접촉과 접촉 힘을 추정합니다. 많은 방법론에서 전신 동역학(Full-Body Dynamics)을 사용하지 않고 일부 단순화 가정을 사용해 정확성을 일부 포기하는데, MCP-EP에서는 DDP와효율적인 구현을 통해 전신 동역학을 사용하면서도 실시간 처리가 가능합니다.

System and Contact Modeling

로봇의 상태에 대한 시스템 모델은 아래와 같이 정의됩니다.

\[\dot x(t) = f(x(t), u(t), \lambda(t)) \quad x(0) = \tilde x\] \[\lambda(t) = \{\lambda_1(t), \lambda_2(t), ...,\lambda_k(t) \} \in \mathbb R^{3 \times k}\] \[\lambda_i(t) = g(x(t); \theta_i), \quad \theta_i = h(\tilde r_{c, i}, \tilde\lambda_i), \quad \forall i = \{ 1, 2, ..., k\}\]

시스템 모델($\dot x(t)$)의 입력으로 현재 로봇의 상태(관절 각도, 각속도)와 제어 입력(조인트 토크), 그리고 하나 이상의 접촉으로 전달되는 외력 집합을 받습니다. 외력은 Spring Contact Model으로 표현됩니다. Spring Contact Model은 입력으로 현재 로봇의 상태와 접촉 피드백을 받습니다. 접촉 피드백은 추정되는 접촉 위치와 힘을 바탕으로 계산됩니다.

그런데 이 접촉 모델에서는 계산할 때에는 현재의 제어 입력이 필요하지 않습니다. 만약 제어 입력이 접촉 모델을 계산할 때 필요하다면, 제어 입력의 변화가 접촉력을 변화시키고 접촉력의 변화가 다시 제어 입력의 값을 변화시키는 순환 관계로 인해 최적화를 풀 때 훨씬 더 복잡한 문제가 됩니다. 여기에서는 제어 입력이 접촉 모델에 영향을 주지 않기 때문에 보다 안정적으로 최적화를 수행할 수 있습니다.

Contact-Involved Robot Dynamics

\[M(q)\ddot q + C(q, \dot q) \dot q + g(q) = \tau_c + \tau_{ext}\] \[M: \text{inertia matrix}\] \[C: \text{Coriolis/centrifugal matrix}\] \[g: \text{gravity}\]

접촉이 포함된 로봇의 기본 동역학은 위와 같이 표현됩니다. 각가속도에 관성 행렬을 곱한 값에, 각속도에 코리올리/원심력 행렬을 곱한 값, 그리고 마지막으로 현재 로봇의 각도에 따라 받게되는 중력의 힘의 합이 로봇의 관절에 가해지는 토크와, 외력에 의해 발생하게 되는 토크의 합과 동일합니다. 그리고 이 ‘외력에 의해 발생하는 토크‘는 아래의 식을 통해 구할 수 있습니다.

\[\tau_{ext} = \sum_{i=1}^k J_i^T(q, r_{c, i})\lambda_i\] \[J_i(q, r_{c, i}) \in \mathbb R ^{3 \times n} \quad \text{(positional Jacobian)}\]

위치 자코비안(Positional Jacobian)은 접촉 위치변화에 따른 로봇 관절의 변화 방향을 의미합니다. 예를 들어 우리가 문 손잡이를 당길 때, 손잡이가 우리에게 가하는 힘의 방향이 달라짐에 따라, 우리가 각 팔의 관절에 가해야하는 힘의 방향도 계속 달라지게 되는데, 이를 표현하는게 위치 자코비안입니다. 위의 외력과 모든 관절 토크 사이의 관계식을 통해 전체 동역학 시스템을 표현할 수 있습니다.

Multi-Contact Feedback

로봇이 실제로 외부 환경에 의한 외력이 전달될 때, 구체적으로 실시간 정보가 제어 시스템에 어떻게 전달되는지, 그 과정을 자세하게 살펴봅니다.

\[\theta_i = h(\tilde r_{c, i}, \tilde\lambda_i)\] \[\tilde r_{c, i}:\quad i^{\text{th}}\text{ contact position}\] \[\tilde \lambda_{i} :\quad i^{\text{th}}\text{ contact force}\]

일단 먼저, 다중 접촉 피드백을 하기 위해서는 현재 접촉하고 있는 위치와 방향을 먼저 알아야 합니다. 이걸 알아내는 것도 쉽지 않은 문제인데요, 여기에서는 이전에 연구에서 소개한 MCP-EP 알고리즘을 통해 추정된 위치와 힘을 사용합니다. 이 입력들을 사용해서 Spring Contact Model의 입력에 필요한 파라미터를 계산합니다.

Spring Contact Model

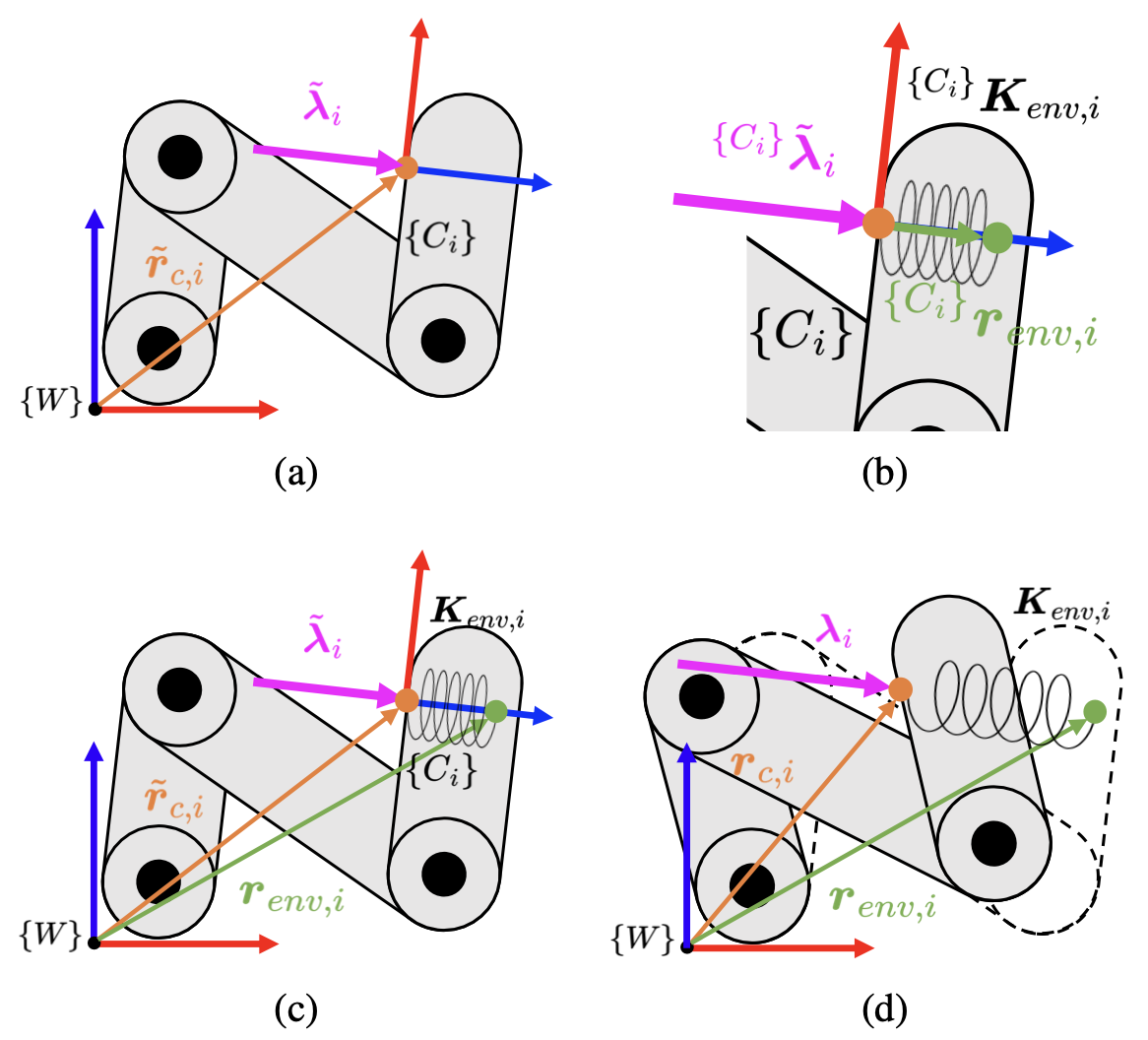
Spring Contact Model은 아래와 같이 정의됩니다.

\[\lambda_i = K_{env, i} \Delta r_i\] \[K_{env, i} \in \mathbb R^{3 \times 3}\] \[\Delta r_i = r_{env, i} - r_{c, i} \in \mathbb R^3, \quad r_{env, i} \text{ is } i^{th} \text{environment location}\]

i번째 접촉 지점에서 발생하는 힘의 크기는 i번째 접촉에 대한 환경 강성 행렬(모든 축방향으로 정의됨)에 환경 지점과 로봇 접촉점 사이의 변위의 곱으로 표현됩니다.

\[\theta_i = \{ K_{env, i}, r_{env, i} \}\]

스프링 모델에 필요한 파라미터 집합은 위와 같습니다. 그러니까 정리하면, 미래에 로봇이 이 지점에 대해 얼마나 위치 변화가 생기는지 알고 있으면, 스프링 모델을 통해 힘을 알 수 있게 됩니다. 접촉 프레임 C의 원점은, 처음에 MCP-EP 알고리즘으로 추정한 접촉 위치($r_{c, i}$)로 설정됩니다. 그리고 힘의 방향은 항상 프레임의 z축으로 설정됩니다. 프레임의 원점($r_{c, i}$)과 스프링 접촉 모델의 탄성 평형점($r_{env, i}$)은 거의 대부분의 경우에 다른 지점입니다.

\[{^{ \{C_i\} }}K_{env, i} = \text{diag}(0, 0, k_{env, i})\]

위와 같이 C의 접촉 강성 행렬은 z축에 해당하는 원소만 0이 아닌 실수 값으로 설정됩니다.

\[{^{ \{C_i\} }} r_{env, i} = {^{ \{C_i\} }} K_{env, i} ^{-1} {^{ \{C_i\} }} \tilde \lambda_i\]

스프링 모델의 탄성 평형 지점은 위의 수식을 통해 구해집니다. MCP-EP 알고리즘으로 추정한 힘의 크기에 환경 강성 행렬을 역으로 취해, C 프레임상의 탄성 평형 지점을 구할 수 있습니다. 여기에서 얻어진 환경 강성 행렬과 스프링 탄성 평형 지점들은 다 C 프레임상의 위치들이기 때문에, 전역 좌표계로 바꿔줘야 합니다.

\[K_{env, i} = R_i {^{ \{C_i\} }}K_{env, i}R_i^T\] \[r_{env, i} = \tilde r_{c, i} + R_i{^{ \{C_i\} }}r_{env, i}\]

전역 환경 강성 행렬을 구할 때 앞 뒤로 회전 행렬을 곱해줍니다. 입력 벡터를 먼저 C 좌표계로 변환하고, 그 좌표계에서 환경 강성 행렬과 곱해진 결과물이 다시 전역 좌표계로 돌아와주는 과정을 밟기 때문에 위와 같이 앞 뒤로 곱해진 형태가 나타납니다.

Contact Feedback Model Predictive Control

이제 위에서 설명한 바탕 지식들을 기반으로, 접촉 상황을 대처하는 모델 제어가 어떻게 수행되는지 설명합니다.

Optimal Control Problem

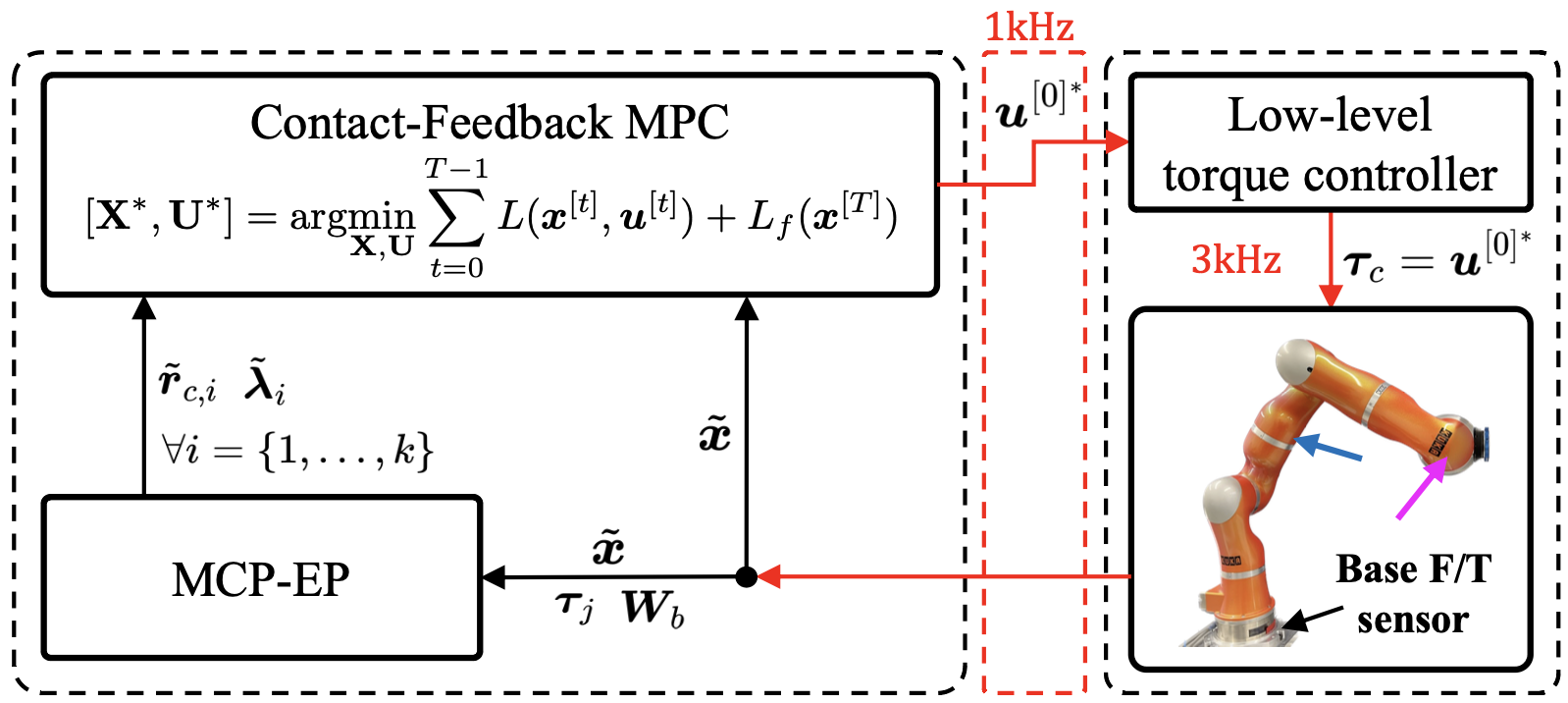
Contact Feedback Model Predictive Control은 아래의 OCP 문제를 해결하는 것으로 표현됩니다.

\[[X^*, U^*] = \underset{X,U}{\text{argmin}} \; \sum_{t=0}^{T-1} L\bigl(x[t],\,u[t]\bigr) + L_f\bigl(x^{[T]}\bigr)\] \[\text{Subject to...}\] \[x^{[t+1]} = F(x^{[t]}, u^{[t]}, \lambda), \quad x^{[0]} = \tilde x\] \[\lambda_i^{[t]} = g(x^{[t]}; \theta_i)\] \[\theta_i = h(\tilde r_{c, i}; \tilde \lambda_i) \quad \forall i = \{1, 2, ..., k\}\] \[x^{[t]} = \in \mathcal{X} \quad \forall t = \{1, 2, ..., T\}\] \[u^{[t]} \in \mathcal{U} \quad \forall t = \{1, 2, ..., T-1\}\]

위의 OCP를 iteratively하게 풀어가면서 계속 새로운 스텝을 밟아나갑니다. 그러니까 0번째 시간 스텝에서 1부터 T까지의 모든 시간 스텝을 계획하기는 하지만, 실제로 1번째 시간 스텝에서 얻은 정보를 토대로 다시 최적화를 수행하는 과정을 반복합니다.

Numercial Solution of OCP

위에서 제시된 최적화 문제를 빠르게 풀기 위해서 DDP(Differential Dynamic Programming) 알고리즘을 사용합니다. 그 중에서도 입력에 직접적인 제약을 설정할 수 있는 Box-FDDP를 사용합니다. 그런데, Box-FDDP에서는 제어 입력에 대한 제약 설정만 제공하고, 관절 상태에 대한 제약은 제공하지 않습니다. 그래서 관절 상태에 대한 Hard Constraints를 설정하기 어려운데요, 이를 해결하기 위해서 상태에 설정하고자 하는 범위를 초과할 경우, 강한 손실 함수 규제를 부여합니다. 이를 통해 관절 각도, 속도를 연산 수행 동안 제한할 수 있습니다.

DDP도 미분 값을 사용해서 최적화를 수행합니다. 자동 미분이나 유한차분법을 사용하면 시간이 오래 걸려 로봇 도메인에서 요구하는 Real-Time Control을 하기 어렵습니다. 따라서 해석적인 방법을 사용하는데, 로봇 정기구학에 대한 해석적 편미분 방정식은 다른 연구에서 이미 구해져 있습니다. 이 논문에서 해석적 방법을 사용하기 위해 추가로 필요한 부분은 스프링 모델의 해석학적 편미분 방정식이고, 그 식은 아래와 같습니다.

\[\frac{\partial\lambda_i}{\partial q} = -K_{env, i}J_i(q, r_{c, i}), \quad \frac{\partial\lambda_i}{\partial \dot q} = \frac{\partial\lambda_i}{\partial u} = 0\]

Cost Function Design

마지막으로 손실 함수가 어떻게 설계되는지 살펴봅니다.

\[l(x,u) = l_m(x) + l_c(\lambda_i) + c_u \|u - u_0\|^2\] \[l_f(x) = l_m(x) + l_c(\lambda_i)\]

손실함수는 크게 Running Cost와 Terminal Cost로 분류됩니다. Running Cost는 매 시간 스텝마다 토크를 과도하게 쓰거나, 불필요한 이동을 포함하는지를 확인합니다. 그리고 Terminal Cost에서는 가장 마지막 최종 상태가 우리가 원하는 목표와 가까운지를 확인합니다. 그리고 각 손실은 Motion Control과 Contact Forct Control의 조합으로 이루어집니다.

Motion Control

\[l_m(x) = c_v \|\dot{q}\|^2 + c_p \|p_{ee}(q) - p_{des}\|^2 + c_r \|R_{ee}(q) \ominus R_{des}\|^2\]

Motion Control 손실은 관절 속도의 크기, end-effector의 위치 오차와 방향 오차의 합으로 정의됩니다.

Contact Force Control

\[l_{c,\text{reg}}(\lambda_i,\gamma_{\text{set}}) = \begin{cases} c_\lambda \|A_d (\lambda_i - \lambda_{i,\text{des}})\|^2, & \text{if } \gamma_i \in \gamma_{\text{set}}, \\ 0, & \text{otherwise}. \end{cases}\]

Contract Force Control은 링크마다 접촉력의 크기를 제어하기 위해 사용됩니다. $A_d$는 힘의 방향을 나타내는 행렬입니다.

\[l_{c,\text{bar}}(\lambda_i,\gamma_{\text{set}}) = \begin{cases} c_\lambda \left(\|\lambda_i\| - \lambda_{i,\text{max}}\right)^2, & \text{if } \|\lambda_i\| > b\,\lambda_{i,\text{max}} \text{ and } \gamma_i \in \gamma_{\text{set}}, \\ 0, & \text{otherwise}. \end{cases}\]

예상치 못한 접촉을 다루기 위해 허용되는 힘의 크기 자체를 제한합니다. 위와 같이 허용치를 벗어나는 경우에 한해, 그 양 만큼을 손실함수에 추가합니다.

Experiments

실험으로 DLR-KUKA LWR IV+ 토크 제어 로봇을 사용합니다. 7 자유도를 가지기 때문에 상태 변수의 차원은 관절각과 관절속도를 쌍으로 포함하므로 14차원, 제어 입력은 각 관잘마다 한 개 이기 때문에 7차원입니다. 베이스에 센서를 부착해 MCP-EP 알고리즘을 사용합니다.

With and Without Contact Feedback

위와 같이 장애물이 세워져 있을 때, 로봇이 어떻게 작업을 수행하는지 살펴봅니다. 로봇의 end-effector는 점점 desired 위치로 이동하면서 철 막대기에 의한 힘을 받게 되는데, 로봇이 계획을 수행하면서 받게되는 접촉력은 아래와 같습니다.

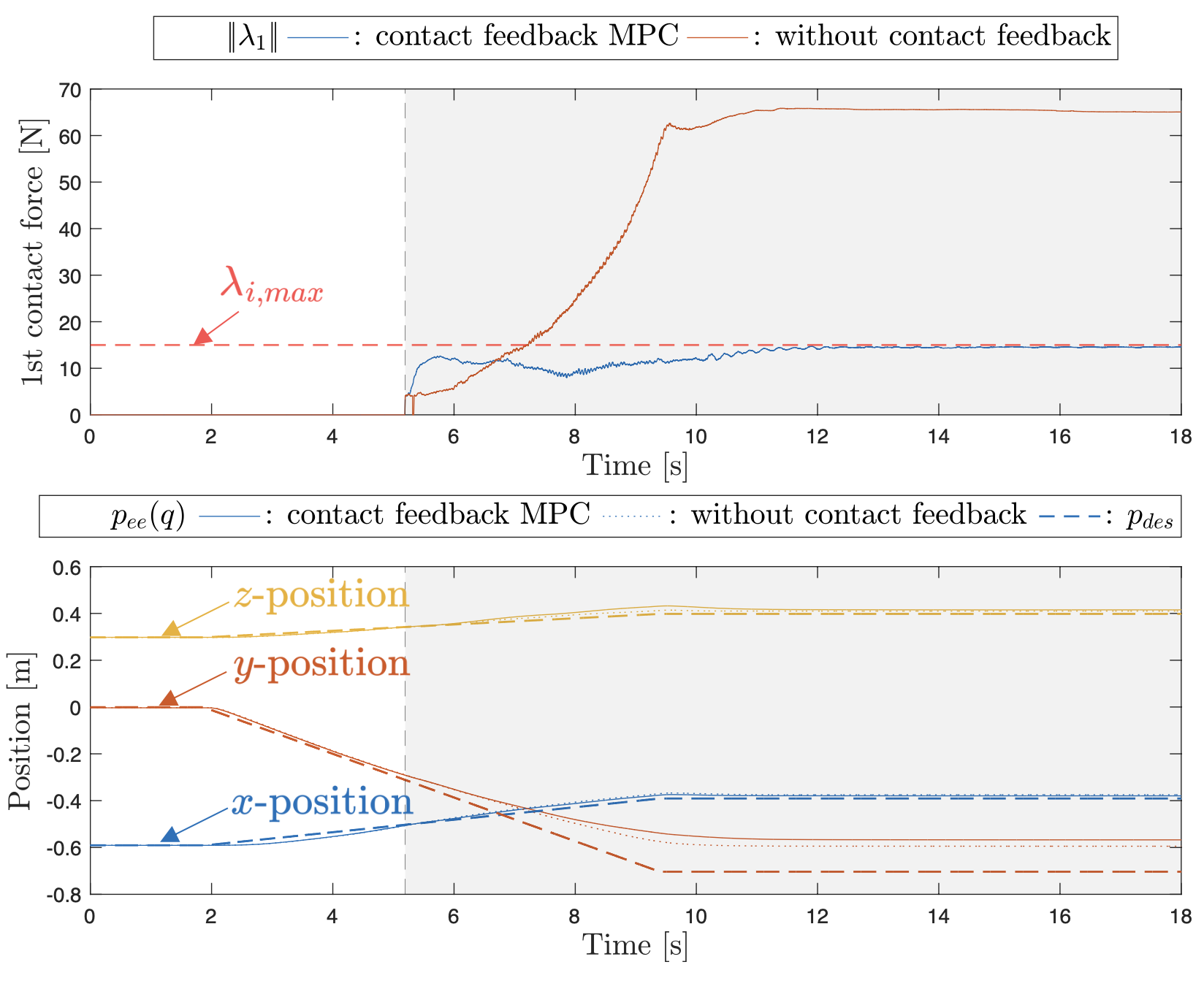
접촉 피드백을 사용하지 않는 경우에는 접촉력이 계속 꾸준히 증가하여 65.87N까지 이르게 되는 반면, 접촉 피드백을 사용하는 경우 미리 설정해 둔 15N 이상으로 접촉력이 증가하지 않는 것을 위의 첫 번째 그래프에서 확인할 수 있습니다. 반면, desired 위치와의 오차는 크게 차이가 나지 않는 것으로 보입니다.

Hybrid Motion-Force Control under Multi-Control

다음으로 Hybrid Motion-Force Control을 할 때에도 접촉에 잘 대응하는지 확인합니다. 말단 이펙터는 yz 평면에 원형을 그림과 동시에 x축 방향으로 20N의 힘을 유지하는 태스크를 수행합니다. 로봇 팔이 태스크를 수행하는 도중 실험자가 세 번째 링크에 접촉 힘을 10초가량 가합니다. 이후 접촉 힘을 해제하고 나서 정적인 힘을 주는 태스크로 전환되고 해당 상태에서의 오차를 측정합니다.

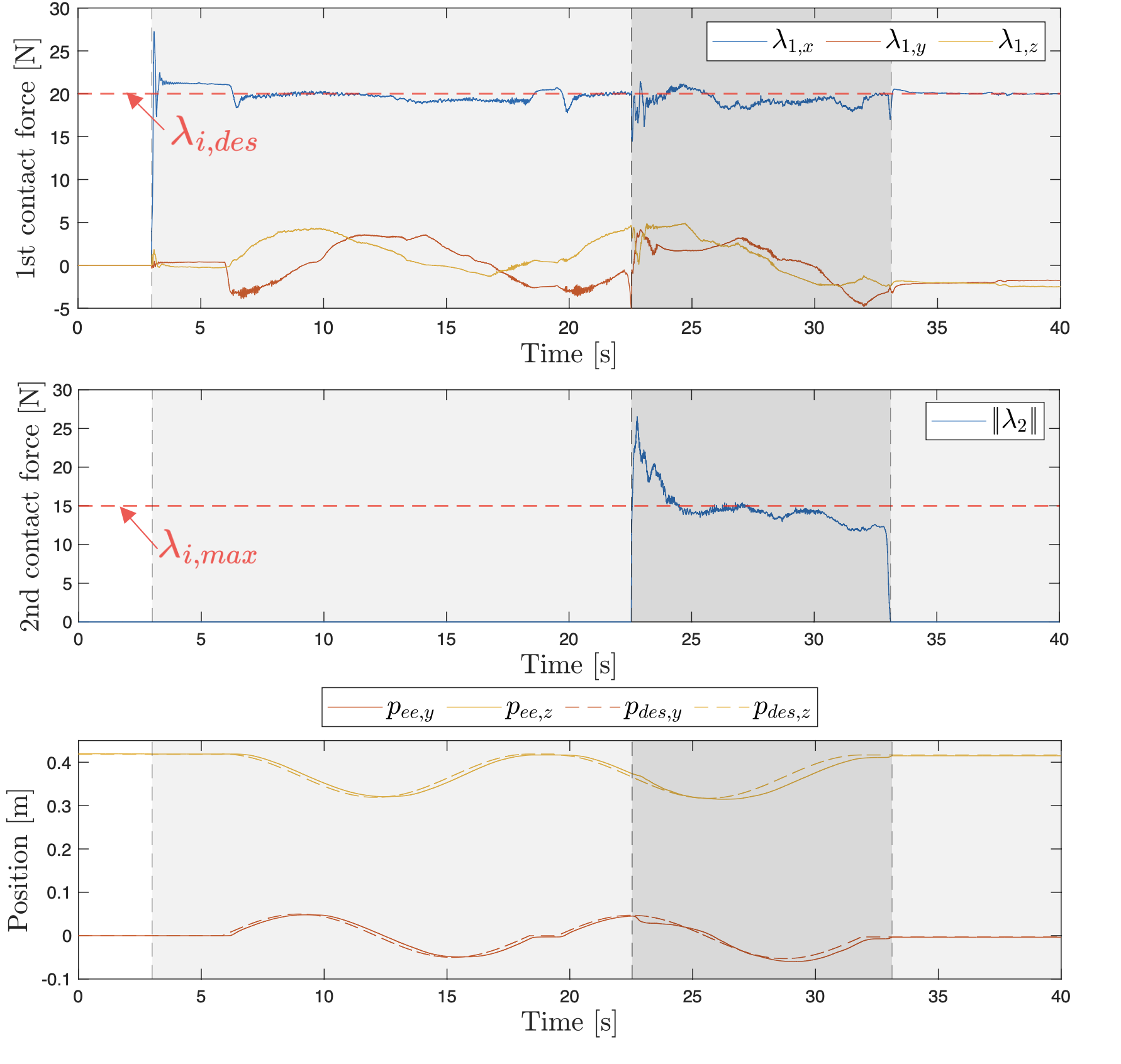
인간의 접촉 힘 없이 벽면에 대해서만 20N의 제약이 있을 때, RMSE로 위치 오차는 0.86cm, 힘 오차는 0.58N으로 나타납니다. 이어서 인간 실험자의 세 번째 링크에 대한 접촉 힘에 대해 15N 이하의 접촉 힘 제약이 추가되었을 때, RMSE로 위치 오차는 1.14cm. 힘 오차는 0.89N으로 소폭 상승합니다. 마지막으로 고정된 자세에서 접촉힘 제어를 수행할 때에는 RMSE로 위치오차는 0.2cm, 힘 오차는 0.1N으로 나타납니다.

추가 실험

논문에 소개되지 않은 실험으로, 고정된 상태에서 물체를 로봇 팔 위에 올렸을 때, 위치 오차가 어떻게 발생하는지 확인하는 실험과, 그렇게 올려둔 상태에서 제어를 할 때, 위치 오차가 오차가 어떻게 발생하는지 확인하는 추가 실험이 있습니다.

Conclusion

스프링 접촉 모델과 MCP-EP를 활용해 Contact-Feedback MPD를 제안해, 다중 접촉 상황에서도 7 자유도 로봇 팔이 실시간으로 이를 처리할 수 있음을 실험적으로 입증한 점에서 의의가 있습니다. 향후 연구로 긴 예측 지평을 사용할 때 매우 큰 접촉력이 발생할 수 있는 가능성, 그리고 접촉이 사라졌을 때의 대처, 마지막으로 환경 강성을 온라인으로 결정해야하는 방법의 필요성 등의 문제를 개선하는 방향을 제시합니다.