LINGO-Space: Language-Conditioned Incremental Grounding for Space
이 포스팅은 ‘Lingo-Space: Language-Conditioned Incremental Grounding for Space‘에 대한 내용을 담고 있습니다.
논문 주소: https://arxiv.org/pdf/2402.01183
Lingo-Space: Language-Conditioned Incremental Grounding for Space
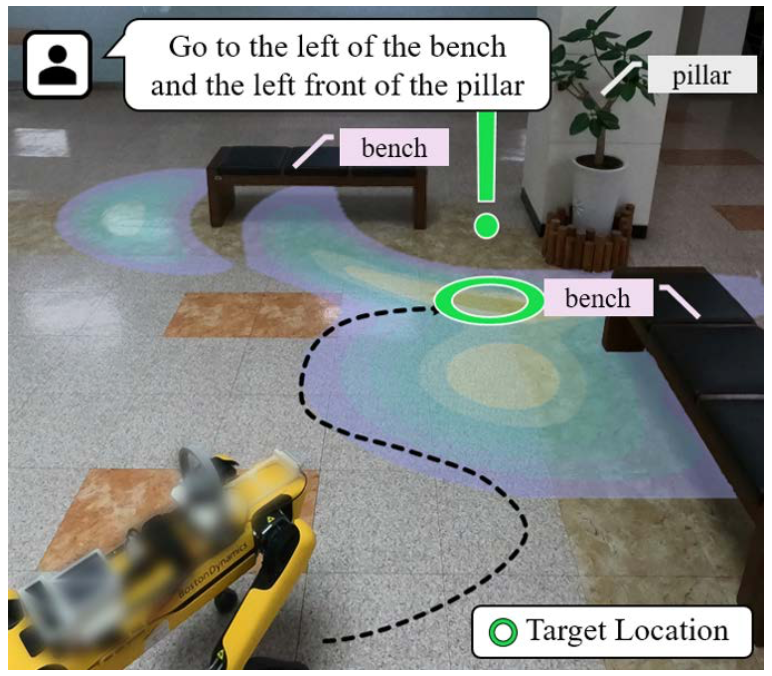
자연어로 로봇에게 지시를 전달하는 방법에 대한 많은 연구가 있어왔습니다. 이전 연구들은 특정 객체, 행동, 또는 사건을 어떻게 식별시킬 수 있는지를 집중해서 다루었습니다. 그러나, 실제 물리 환경에서 로봇에게 인간의 지시를 수행하도록 맡기기에는 여전히 어려움이 많습니다.
지시어에 포함된 spatial reference를 찾아내 문제를 해결하는 것을 Space Grounding이라고 부릅니다. 그동안의 전통적인 grounding과 달리 Space grounding은 인간의 지시어가 가지는 내재적 모호성을 다루어야 하기 때문에 훨씬 더 복잡합니다. 게다가 대부분의 지시문은 지시의 연속으로 구성되는데, 이전 연구에서는 명확한 구분 없이 한 번에 지시문 전체를 인코딩한다는 문제가 있었습니다.
LINGO-Space에서는 위의 문제점들을 해결하기 위해 Incremental grounding을 사용합니다.
Problem Formulation
\[x^* = \text{argmax}_x P(x \mid \Lambda, \mathcal O)\] \[= \text{argmax}_{x} \int \int _{\theta,\Upsilon_{sg}} P(x \mid \theta) \, P(\theta \mid \Lambda, \Upsilon_{sg}) \, P(\Upsilon_{sg} \mid \mathcal O)\] \[x^* \in \mathbb R^2\] \[\Lambda: \text{natural language insturction}\] \[\mathcal O = \{o_1, o_2, ..., o_N\}: \text{object set in the environment}\] \[\theta: \text{probability distribution parameter}\] \[\Upsilon_{sg}: \text{scene graph}\]문제에서 찾아야 하는 것은 주어진 환경에서 지시 문장을 가장 잘 표현하는 위치입니다. 위치에 대해 추정하는 분포가 있다면, 그 분포 중 가장 확률이 높은 위치가 모델의 추정 정답이 됩니다. object set만을 보고 바로 분포를 추정하기 어렵기 때문에, object set에서 먼저 물체 사이의 관계를 표현하는 scene graph를 생성합니다. 그런 다음, scene graph와 지시문을 바탕으로 목표 위치의 분포를 추정하고, 그 분포 상에서 가장 확률 값이 높은 지점이 모델의 추정 정답입니다.
\[\underbrace{P(x \mid \theta_M)}_{\text{Location Selector} } = \prod_{i=1}^{M} \underbrace {[P(\theta_i \mid \theta_{i-1}, \Lambda^{(i)}, \Upsilon^*_{sg})}_{\text{Spatial-distribution estimator}} \underbrace{ P(\Lambda^{(i)} \mid \Lambda, \Upsilon^*_{sg})}_{\text{Sematic parser}} ]\]위는 지시 문장 하나에 여러 공간 표현이 나타날 때를 처리하기 위해 변형한 목적 함수입니다. 만약에, 지시어가 ‘상자의 오른쪽에 둔 다음, 그 상태에서 벤치에 좀 더 가까워지게 옮기세요’ 였다면, ‘상자의 오른쪽’ 을 표현하는 분포를 구하고, 해당 분포를 바탕으로 ‘벤치에 좀 더 가까워지게’ 를 표현하는 분포를 이어서 예측하는 방식으로 최종적인 분포를 구할 수 있습니다.
Methodology: LINGO-Space
우리에게 주어지는 것은 object set과 지시문 뿐입니다. 이 정보들로부터 지시문에 포함된 공간 표현들을 분리해 낼 수 있어야 하고, 관측된 object set으로부터 scene graph를 뽑아내야 합니다. 그리고 마지막으로, 이 정보들을 토대로 Spatial-Distribution을 추정해내고, 이 추정된 분포를 통해 지시문을 수행하기 위한 최종 위치를 결정하게 됩니다.
A Scene-Graph Generator
\[\Upsilon_{sg} = (\mathcal V, \mathcal E)\] \[f^u = \{f^u_{\text{coord}}, f^u_\text{box}, f^u_\text{viz}\}\] \[f^u_{\text{coord}} \in \mathbb R^2\] \[f^u_\text{box} \in \mathbb R^4\] \[f^u_\text{viz} \in \mathbb R ^{D_{\text{viz}}}\]노드는 특징으로 총 세 개의 원소를 가집니다. 하나는 2차원 평면 상의 xy 좌표(2차원), 그리고 그 물체가 존재하는 bounding box(각 축별로 최대, 최소 범위를 정해야 하므로 4차원), 마지막으로 crop된 이미지를 CLIP 이미지 인코더로 얻게되는 visual feature를 원소로 갖습니다.
\[e_{uv} \in \mathcal E\] \[f^{uv}_\text{edge} \in \mathbb R ^{D_{\text{txt}}}\]그래프의 엣지는 물체(노드) 사이의 공간적 관계를 나타냅니다. 물체의 위치와 박스 정보를 토대로 두 물체 사이의 관계를 결정합니다. 예를 들어, 두 물체의 거리가 특정 거리 이하가 되면 ‘near‘라는 술어로 두 노드를 연결하는 엣지를 표현합니다. 그렇게 술어가 결정되면 술어 상태로 두는게 아니라, CLIP 텍스트 인코더를 통해 벡터 표현으로 변환합니다.
A Semantic Parser
다음으로 복합 지시문에 포함된 공간 참조 표현을 LLM(Chat-GPT)를 통해서 분리합니다. 복합 지시문에는 주요 동작과 대상에 대한 정보가 있고, 그 외에 추가적인 공간적 관계가 포함됩니다. 논문에서는 이 두 종류의 정보를 적절한 프롬프트 엔지니어링을 통해 LLM이 semantic parser 역할을 수행할 수 있도록 합니다.
input
put the cyan bowl above the chocolate and left of the silver spoon.
output
{
"action": "move",
"source": "cyan bowl",
"target": [
("chocolate", "above"),
("silver spoon", "left")
]
}
위에서 문장에서 action에 해당되는 단어는 put인데, output에는 move라고 되어 있죠. 이거는 action을 로봇이 수행할 수 있는 skill set 중에 가장 비슷한 skill로 대체해서 그렇습니다. 그 아래에 target에 포함된 순서쌍 들도 그대로 두는 것이 아니라, CLIP 텍스트 인코더를 사용해 feature vector 형태로 바꿔놓습니다.
A Spatial-Distribution Estimator
이제 각 공간 참조 표현에 따른 분포를 어떻게 좁혀나가는지 살펴봅니다.
Spatial Distribution
\[(d, \phi) \sim (\mathcal N(\mu_d, \sigma_d^2), \mathcal M(\mu_\phi, \kappa_\phi))\] \[P\left(x \mid r^{(i)}, \Upsilon_{sg}\right) = \sum_{j=1}^N \, w_j \cdot P\left(d; \mu_{d_j}, \sigma^2_{d_j}\right) \cdot P\left(\phi; \mu_{\phi_j}, \kappa_{\phi_j}\right)\] \[\theta = [(w_1, \mu_{d_1}, \sigma^2_{d_1}, \mu_{\phi_1}, \kappa_{\phi_1} ), ..., (w_N, \mu_{d_N}, \sigma^2_{d_N}, \mu_{\phi_N}, \kappa_{\phi_N} )]\]각 물체 주변의 분포는 위와 같이 가우시안 분포와 폰 미제스 분포를 통해 표현될 수 있습니다. 폰 미제스 분포에서는 위치와 밀집도를 통해 분포가 표현됩니다. 공간 참조 표현은 모호성을 가지기 때문에, 한 참조 표현에 대해 다양한 물체 주변의 분포를 동시에 다루어야 합니다. 예를 들어서, ‘상자 오른쪽’ 이라는 참조 표현이 있으면, scene graph에 존재하는 모든 ‘상자’ 노드에 대해 오른쪽에 해당하는 위치의 확률 값이 높은 분포로 표현되어야 합니다. 따라서 각 노드마다 가중치를 두고, 각 노드를 대상으로 정의된 분포들의 가중 합으로 정의되는 혼합 분포로 표현됩니다.
Pre-processing
\[X_0^{(i, j)} = \text{concat}(\bar{\mathrm f}^j_\text {coord}, \bar{\mathrm f}^j_\text {viz}, \bar{\mathrm f}^{(i)}_\text {ref}, \bar{\mathrm f}^{(i)}_\text {pred}, \bar{\mathrm f}^{(i-1)}_\text {state})\] \[\bar{\mathrm f}^j_\text {coord} = \gamma(\mathrm f^j_\text{coord}) \in \mathbb R^{2(2K + 1)} \quad \gamma: \text{positional encoding}\] \[\bar{\mathrm f}^j_\text {viz} = \mathrm M_\text{viz} \mathrm f^j_\text{viz} \quad \mathrm M_\text{viz} \in \mathbb R^{D_H \times D_\text{viz}}\] \[\bar{\mathrm f}^{(i)}_\text {ref} = \mathrm M_\text{ref} \mathrm f^{(i)}_\text{ref} \quad \mathrm M_\text{ref} \in \mathbb R^{D_H \times D_\text{CLIP}}\] \[\bar{\mathrm f}^{(i)}_\text {pred} = \mathrm M_\text{pred} \mathrm f^{(i)}_\text{pred} \quad \mathrm M_\text{pred} \in \mathbb R^{D_H \times D_\text{CLIP}}\]i번째 참조 표현에 대해서 j번째 물체에 대한 입력은 위와 같이 결정됩니다. 물체의 좌표를 positional encoding해 얻은 벡터, 물체의 시각 정보에 대한 벡터, i번째 참조 표현에 대한 참조 대상과 위치에 대한 벡터들, 마지막으로 바로 이전 모델의 output과 관련된 벡터를 모두 concat해 입력으로 넣어줍니다. 첫 참조 표현이어서 모델의 이전 output이 없는 경우에는 0벡터를 넣어줍니다.
Estimation Network
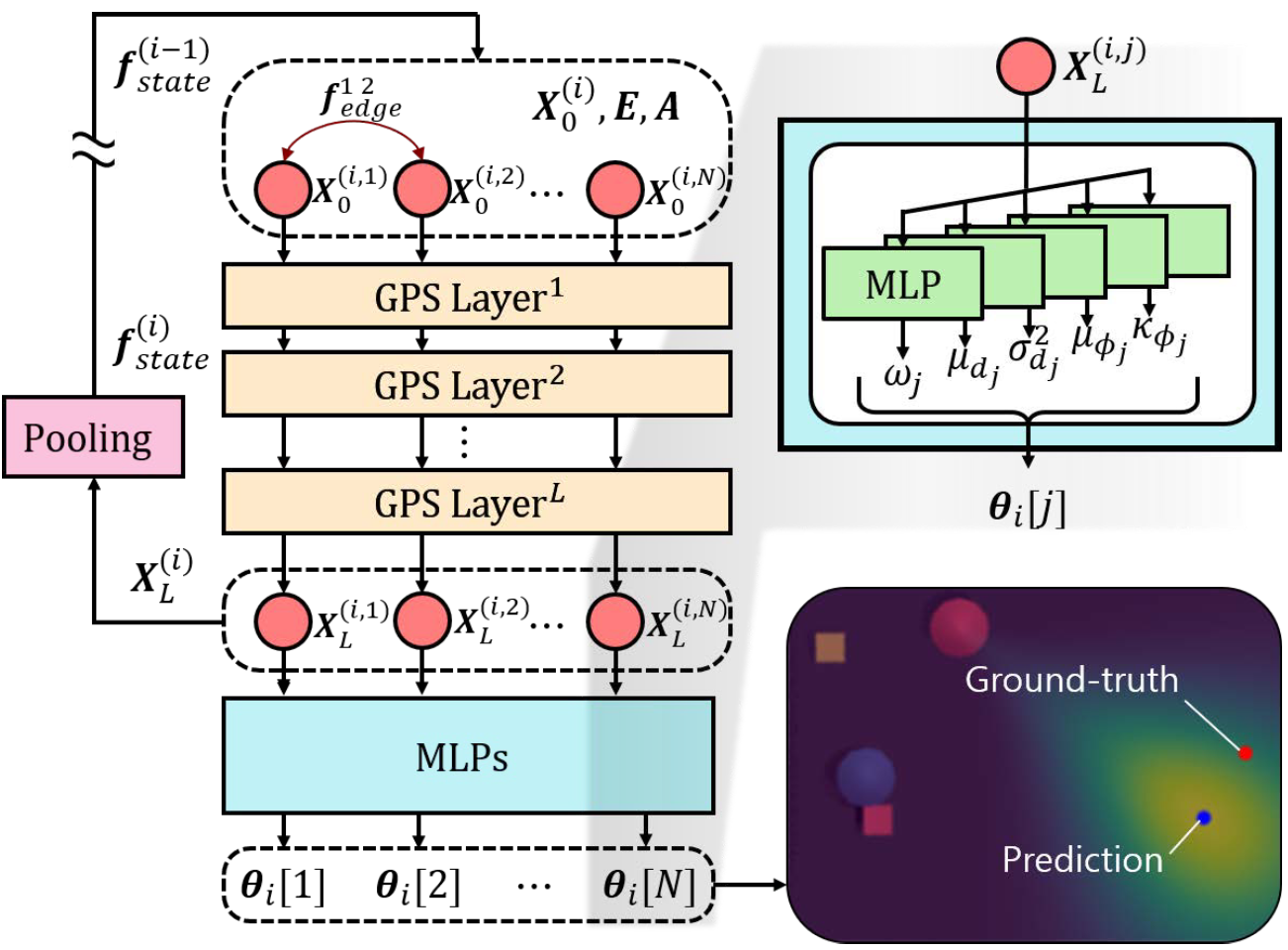
전처리된 각 노드별 특징들, 엣지들의 특징들, 그리고 마지막으로 그래프의 인접 행렬을 GPS의 입력으로 넣어줍니다. GPS 레이어 L개를 통과하개 된 후의 각 노드별로 특징 벡터들을 가지고 적절히 구성된 2층 MLP를 통과시켜 분포를 정의하는 5개 파라미터를 구합니다. 예를 들어, 음수일 수 없는 파라미터에 대해서는 마지막에 softplus 활성화 함수를 취해 양수가 되도록 하고, $\kappa_\phi$는 역수를 예측하게 해, 모델이 좀 더 안정적으로 학습할 수 있도록 합니다. 나머지 파라미터들도 적절한 구조를 채택해 범위가 잘 대응될 수 있도록 합니다.
위의 과정을 모든 참조 표현에 대해 반복하고, 마지막으로 얻은 파라미터를 이용해 최종 분포를 얻습니다.
Objective Function
\[\mathcal L = \lambda \mathcal L_1 + (1-\lambda)\mathcal L_2\] \[\mathcal L_1 = -\log\!\Biggl( \sum_{j=1}^{N} w^{\text{des}}_j \cdot P\bigl(x^{\text{des}}; \mu_{d_j},\, \sigma_{d_j}^2,\, \mu_{\phi_j},\, \kappa_{\phi_j}\bigr) \Biggr)\] \[\mathcal L_2 = -\frac{1}{N} \sum_{j=1}^{N} w^{\text{des}}_j \cdot \log\!\bigl(w_j\bigr)\]손실 함수는 공간 분포의 negative log-likelihood와 각 노드의 가중치에 대한 cross entropy의 가중합으로 정의됩니다. 이를 통해 혼합 분포가 해당 지점에 높은 확률을 부여하도록 하고, 중요한 노드에 큰 가중치를 할당하도록 만듭니다.
Experiment Setup
실험으로 총 두 가지를 실험합니다. 단일 참조 표현에 대해서 성능 향상이 얼마나 있는지, 그리고 다중 참조 표현을 포함하는 복합 지시문일 때 성능이 얼마나 향상되는지 각각 측정합니다. 그리고 이어서 실제 환경에서도 제안된 방법론이 잘 통하는지 확인합니다.
Grounding with a Referring Expression
단일 참조 표현이 있는 지시문에서 테이블 위의 객체 배치를 추론하는 상황에서 성능을 측정합니다. PyBullet 시뮬레이터를 사용하고, 네 가지 벤치마크에서 총 세 가지 베이스라인 기법과 비교합니다.
- CLIPort’s benchmark: 물체를 참조되는 객체 내부에 집어넣는 과제
- ParaGon’s benchmark: 동일한 객체가 여러 개 존재하는 상황에서 물체를 올바르게 위치시키는 과제
- SREM’s benchmark:
- LINGO-Space’s benchmark: ‘close-seen-color’, ‘close-unseen-color’, ‘far-seen-color’, ‘far-unseen-color’ 라는 네 가지 테스크를 SREM’s benchmark에 추가로 포함시킴
Grounding with Multiple Referring Expressions
여러 참조 표현이 포함된 복합 지시문을 잘 처리하는지 확인합니다. 기존의 벤치마크는 복합 지시문 상황과 조금 거리가 있기 때문에 composite 이라는 새로운 태스크를 만들어 사용합니다. CLIPort 처럼 테이블 위의 시나리오를 가정하고, 총 10개의 방향을 나타내는 지시어가 사용됩니다. 훈련을 할 때는 한 개에서 세 개의 참조 표현이 사용될 수 있고, 테스트를 할 때에는 6개까지 참조 표현이 포함됩니다. 모든 관계를 만족하는 위치는 한 개만 존재하도록 만들었고, 동일한 물체가 존재하거나 방향을 나타내는 지시어가 반복되어 사용되는 경우는 포함하지 않습니다. 추가로 SREM에 다중 참조 표현 지시문에 대한 태스크가 있는데, 이것도 함께 평가합니다.
Evaluation
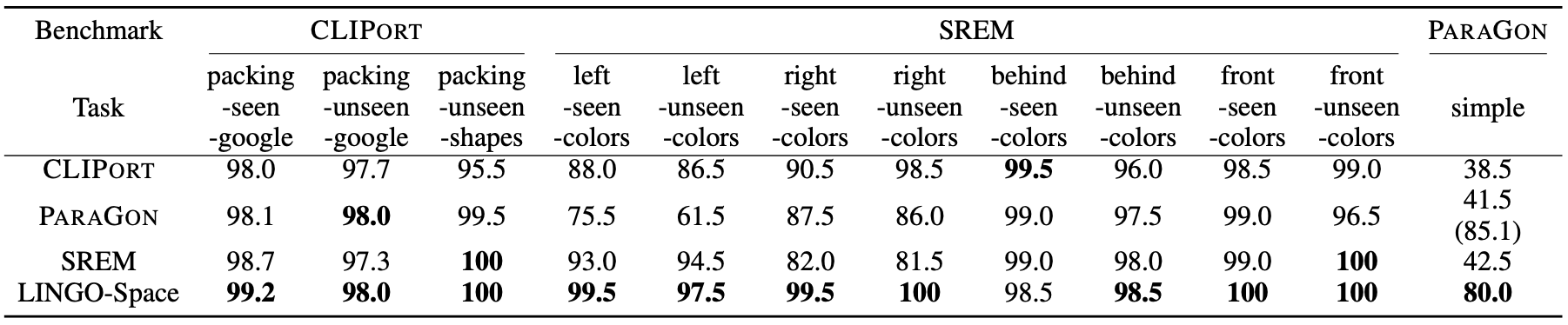
단일 참조 표현에서 총 12개의 벤치마크로 평가를 수행했는데, 11개의 경우에서 LINGO-Space가 가장 높은 점수를 보여줍니다. 또한 미학습 물체에 대해서 높은 성능을 보여줍니다. ‘behind-seen-colors’ 태스크에서 성능이 조금 깎여서 나오는데, LINGO-Space 모델이 물체의 부피를 처리하지 못해 겹치는 상황이 발생해 실패가 발생합니다. SREM이 ‘simple’ 태스크에 있어서 성능이 꽤 낮은데, 사전에 정의된 지시어 구조에 의존적인 특징 때문인 것으로 보입니다.
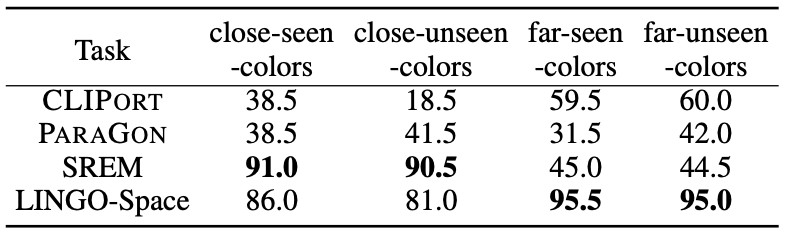
위에서 거리와 관련된 술어가 추가된 상황에서도 LINGO-Space는 꽤 준수한 성능을 보여줍니다. 특히 ‘far’ 이라는 술어에 대해 성능이 높은 것을 보아, 확률 분포 표현이 다양한 거리 개념을 표현하는데 능하다는 점을 보여줍니다.
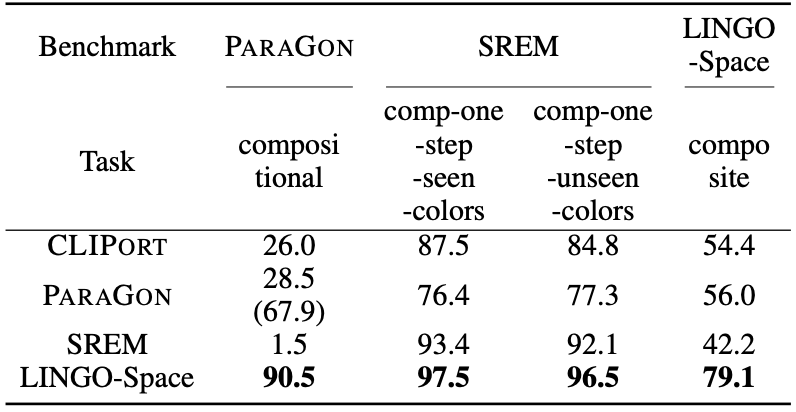
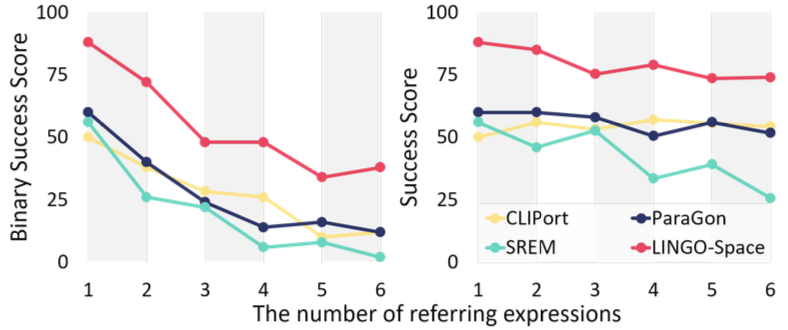
위는 복합 지시문에 대한 평가인데, 모든 상황에 대해 LINGO-Space가 가장 높은 성능을 보여줍니다. 추가로 실제 세계에서 Spot 로봇에 알고리즘을 적용해 보았는데, 라이다로 scene graph를 만들고 ‘move to the front of the red box and close to the tree’라는 지시문을 전달했는데, 성공적으로 목표 분포를 만들고 최적 위치에 잘 도달하는 것을 확인할 수 있었습니다.
Conclusion
LINGO-Space는 여러 참조 표현을 포함하는 복합 지시문을 수행하기 위해, GPS로 polar 분포를 예측하고 이를 혼합해 최종적인 확률 분포를 예측하는 방법으로, 단일 참조 표현에 대해서도 좋은 성능을 보여줍니다. 특히 여러 참조 표현이 포함된 복합 지시문에서 다른 베이스라인과 비교했을 때 큰 성능 차이를 보여주고, 실제 4족 Spot 로봇에서 사용될 수 있음을 보인 점이 인상깊습니다.
댓글남기기