Learning-based Adaptive Control of Quadruped Robots for Active Stabilization on Moving Platforms

이 포스팅은 ‘Learning-based Adaptive Control of Quadruped Robots

for Active Stabilization on Moving Platforms‘에 대한 내용을 담고 있습니다.

논문 주소: https://sgvr.kaist.ac.kr/~msyoon/papers/IROS24/IROS_2024_MS_vCM.pdf

Learning-based Adaptive Control of Quadruped Robots for Active Stabilization on Moving Platforms

4족보행 로봇에게 있어서 중심 잡기는 항상 중요한 과제입니다. 때문에 다양한 지형 환경에서 중심을 잡을 수 있도록 많은 연구가 있어왔습니다. 4족보행 로봇이 점차 다양한 곳에 적용됨에 따라, 지하철, 버스와 같이 움직이는 플랫폼 위에서 중심을 잡 잡을 수 있는 능력이 중요해지고 있습니다. 수직 운동이나 피치 변화에 대응할 수 있도록 한 이전 연구가 있었지만, 알려지지 않은 3차원 공간상의 모든 회전변환(6자유도 motion)에서 중심을 잡을 수 있도록 하는 문제는 이 논문에서 최초로 다룹니다. 이 논문에서는 이 문제를 해결하기 위해 강화학습 기반의 알고리즘인 LAS-MP(Learning-based Active Stablization mothod on Moving Platforms)를 제안합니다.

LAS-MP

LAS-MP가 어떻게 6자유도의 광범위한 모션에도 불구하고 플랫폼 위에서 중심을 잡을 수 있게 하는지 아래에서 설명합니다.

Challenges & Motivation

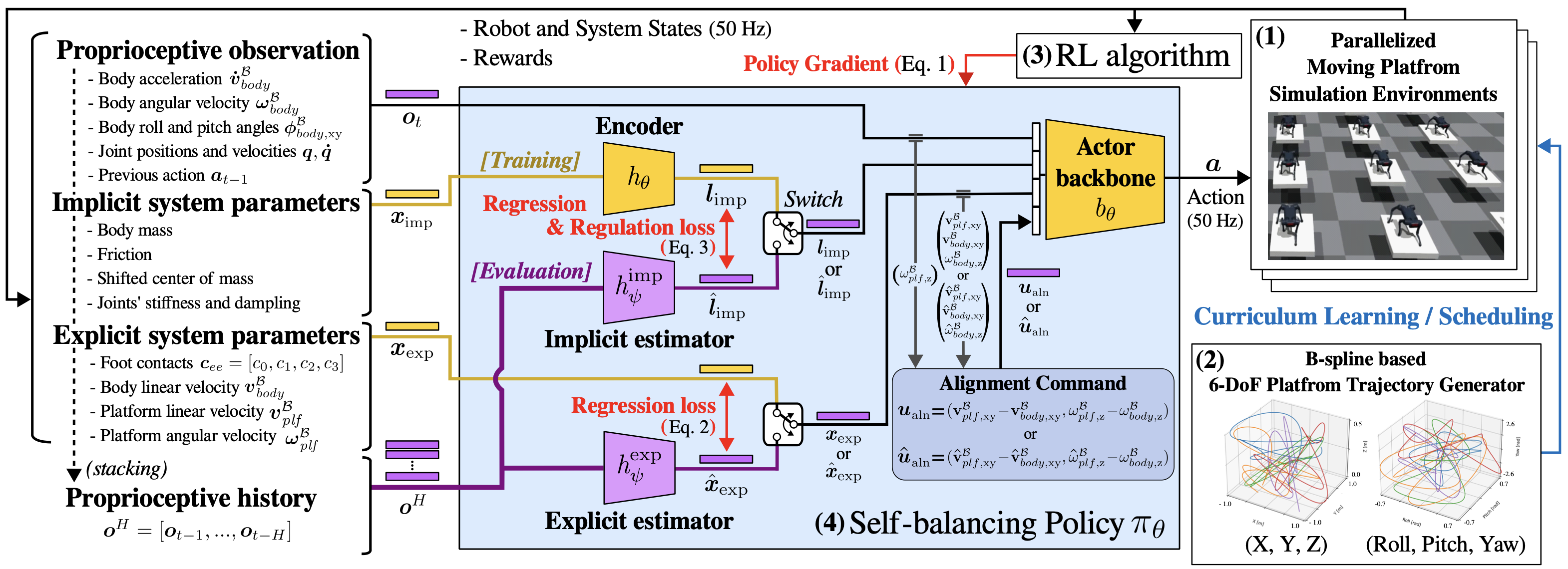
6자유도의 플랫폼 모션은 굉장히 다양한 종류의 힘을 발생시킵니다. 수평방향의 모션은 관성력을 발생시키고, 급격한 회전 모션은 원심력을 발생시킵니다. 갑자기 위로 치솟는 모션은 수직항력을 더하게 되고, 그 반대의 경우에는 지면과의 수직항력과 마찰력을 상실시키게 할 수 있습니다. 플랫폼의 움직임을 미리 알 수만 있다면 이런 힘들에 대해 대처할 수 있겠지만 실제 환경에서는 플랫폼의 움직임이 알려지지 않는 경우가 많고, 이 경우 반응이 지연되어 균형을 재빨리 회복하기 어렵습니다. 위의 문제점들을 해결하기 위해서 이 논문에서는 강화학습을 사용해 플랫폼의 모션과 로봇의 상태를 예측합니다. 그렇게 예측한 정보를 바탕으로 보다 빠르게 플랫폼의 변화에 대해 대처할 수 있도록 해줍니다. 위 그림에서 알고리즘의 전체적인 동작과정을 살펴볼 수 있습니다.

Variable Notation

\[p^{\mathcal{W}}_{\langle \cdot \rangle,[\cdot]} \in \mathbb{R}^3 \text{ : position}\] \[\mathcal W \text{ : world coordinate}, \quad \mathcal P \text{ : platform coordinate}, \quad \mathcal B \text{ : body coordinate}\] \[\langle\cdot\rangle \text{ : body, plf, }ee_i\] \[[\cdot]\text{ : specific elements in a variable}\]

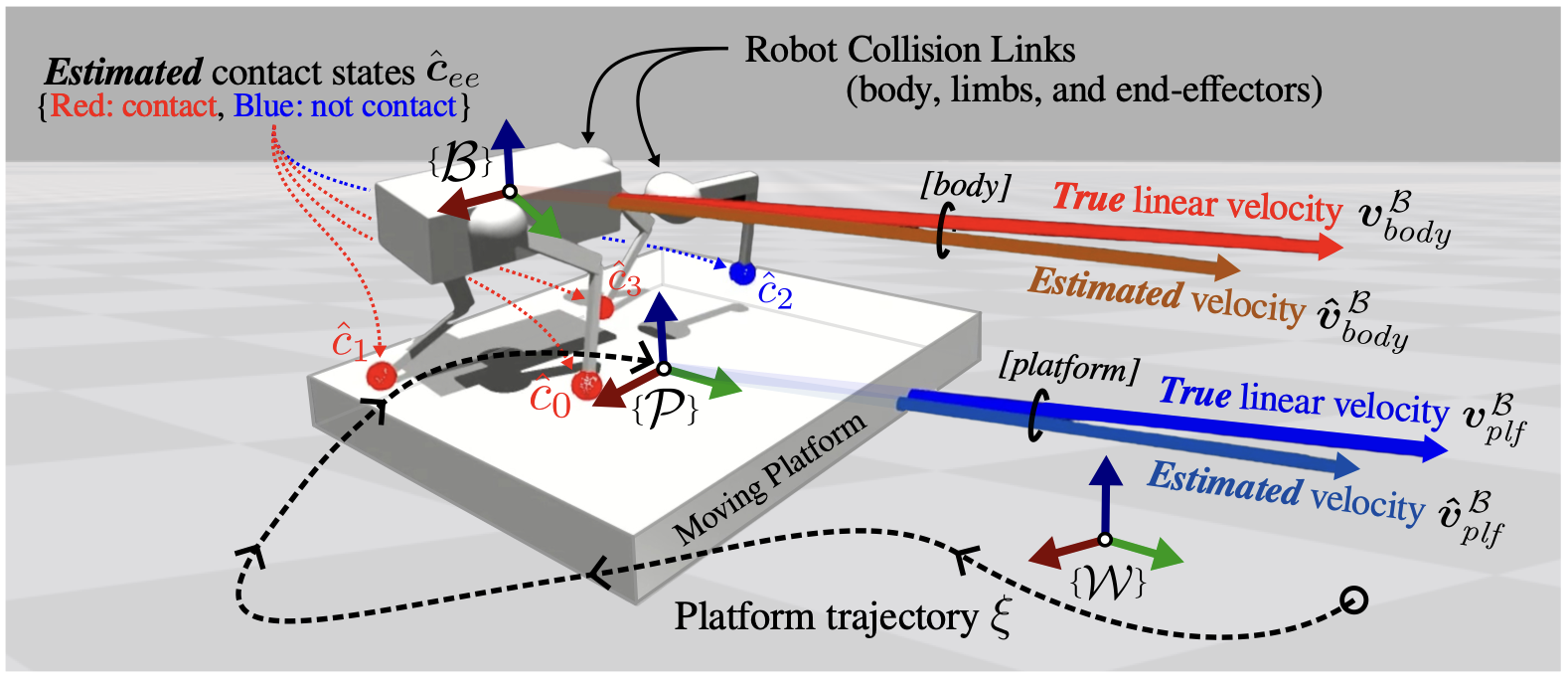
사용되는 좌표계의 종류는 로봇 좌표계, 플랫폼 좌표계, 그리고 월드 좌표계가 있으며, 변수의 윗첨자로 이를 표시해 나타냅니다. 그리고 아랫첨자로는 대상이 무엇인지, 그 대상을 표현하는 변수가 많다면 그 중에 무슨 변수인지를 나타내는데 사용합니다. 실제값이 아닌 추정값인 경우에는 $\hat\cdot$ 표시로 이를 명시합니다. 아래는 그 외의 기본적인 표기법들입니다.

\[v, \dot v \in \mathbb R^3\text{ : velocity, acceleration}\] \[\phi, \omega \in \mathbb R^3 \text{ : Euler angle, angular velocity}\] \[q, \dot q, \ddot q \in \mathbb R^{12}\text{ : joint position, joint velocity, joint acceleration}\] \[c_{ee} = [c_o, c_1, c_2, c_3] \in \mathbb B^4 \text{ : contact states(0 or 1)}\] \[f_{ee} \in [f_o, f_1, f_2, f_3] \in \mathbb R^{4 \times 3} \text{ : contact forces}\] \[\xi \text{ : 6-DoF platform trajectory}\]

Problem Formulation of RL

\[(\mathcal S, \mathcal O, \mathcal A, \mathcal F, \mathcal R, \mathcal Q_0, \gamma)\]

이 논문에서는 중심잡기 문제를 POMDP로 정의하는데, 이는 플랫폼의 움직임에 대한 정보가 주어지지 않기 때문입니다. 문제 정의는 위와 같이 7개의 원소를 가지는 튜플로 구성되고 각 원소는 아래와 같습니다.

\[\mathcal S \text{ : state space}\] \[\mathcal O \subset \mathcal S \text{ : observation space}\] \[\mathcal A \text{ : action space}\] \[\mathcal F: \mathcal S \times \mathcal A \rightarrow \mathcal S \text{ : transition space}\] \[\mathcal R : \mathcal S \times \mathcal A \rightarrow \mathbb R \text{ : reward function}\] \[s_o \sim \mathcal Q_0 \text{ : initial state}\] \[\gamma \in [0, 1) \text{ : discount factor}\]

각 에피소드에서 로봇은 플랫폼의 중심에 위치하고, yaw 각도가 -180도부터 180도 사이에서 랜덤으로 설정돼 시작합니다.

\[J(\pi_\theta) \;=\; \mathbb{E}_{\xi_{\mathrm{train}} \sim \Xi_{\mathrm{train}}} \Biggl[ \mathbb{E}_{(s,a) \sim \rho_{\pi_\theta}, \; s_{0} \sim Q_{0}} \Bigl[ \sum_{t=0}^{T} \gamma^{t} \, \mathcal R(s_{t}, a_{t}) \Bigr] \Biggr].\] \[\Xi_{\text{train}}: \text{ : training set of platform}\] \[\rho_{\pi_\theta} \text{ : state-action visitaion probability}\]

목적함수는 위와 같이 여느 강화학습 문제들과 동일한 형식을 가집니다. 이어서 위 각 원소들이 구체적으로 어떻게 정의되고 사용되는지 알아봅니다.

Learning Self-Balancing Policy

강화학습 에이전트는 플랫폼의 모션 정보를 토대로 액션을 선택하도록 설정됩니다. 그런데 실제 상황에서는 플랫폼의 모션 정보와 같은 특권 정보(previleged information)를 알지 못하는 상태로 행동을 선택해야 할 수 있도록 만들어줘야 합니다. 이를 해결하는 가장 기본적인 접근 방법으로 특권 정보를 활용해 Teacher Policy를 학습시키고, 이 Teacher Policy를 모사하도록 하는 Student Policy를 학습시키는 Two-Stage Teacher-Student 방법이 있습니다. 그리고 다른 방법으로 이 논문에서도 사용하는 ROA(Regularized Online Adaptation) 방식이 있습니다. ROA는 특권 정보를 사용해 정책을 학습시키면서도, 특권 정보를 예측하는 추정기를 동시에 학습시켜, 두 단계로 구성되는 Techer-Student 방식과 달리 한 번에 학습시킬 수 있습니다.

Self-balancing Policy

\[b_\theta : \mathcal O \times \mathcal X_\text{exp} \times \mathcal L_\text{imp} \times se(2) \rightarrow \mathcal A \text{ : actor backbone}\] \[h_\theta : \mathcal X_\text{imp} \rightarrow \mathcal L_\text{imp} \text{ : encoder}\]

먼저 로봇의 중심 잡기와 관련된 정책은 입력들을 갖고 행동을 출력하는 actor backbone과 관측정보들을 적절한 latent vector로 바꿔주는 encoder로 구성됩니다. 행동은 관절 변위로, 기존 nominal에 더해져 최종적인 각도가 결정됩니다.

\[o: [\dot v^\mathcal B_{body}, \omega^\mathcal B_{body}, \phi^\mathcal B_{body, xy}, q, \dot q, a_{t-1}]\in \mathcal O\] \[x_\text{exp} = [c_{ee}, v^\mathcal B_{body}, v^\mathcal B_{plf}, \omega^\mathcal B_{plf}] \in \mathcal X_{exp}\] \[x_\text{imp} = [\text{body mass, shifted center of mass, contact friction, stiffness and damping of joint}]\] \[u_\text{aln} = [v^\mathcal B_{plf, xy}, -v^\mathcal B_{body. xy}, \omega^\mathcal B_{plf, z}, -\omega^\mathcal B_{body, z}]\]

backbone의 입력 요소들은 위와 같습니다. observation은 proprioceptive sensor data와 이전의 행동으로 구성되는, 실제 환경에서 우리가 확실하게 알 수 있는 특징들로 구성됩니다. explicit system parameter는 플랫폼과 로봇, 접촉에 관련된 특권 정보들로 구성됩니다. 이 정보를 통해 플랫폼의 움직임에 대응할 수 있게 됩니다. implicit system parameter는 질량과 질량 중심, 마찰력, 관절 강성과 같은 정적인 특권 정보들로 구성됩니다. 이 정보들을 그대로 사용하지 않고 encoder에 통과시켜 얻게되는 latent vector를 사용합니다. 그리고 마지막으로, 플랫폼과 로봇을 정렬시키기 위한 alignment command가 들어갑니다.

System State Estimators

실제 환경에서는 가상 환경과 달리 특권 정보를 사용할 수 없기 때문에 실시간에서 이 정보들을 observation history를 통해 예측해 나갑니다.

\[o^H = [o_{t-1}, ..., o_{t-H}] \in \mathcal O^H\] \[h^{exp}_\psi : \mathcal O^H \rightarrow \mathcal X_{exp}\] \[h^{imp}_\psi : \mathcal O^H \rightarrow \mathcal L_{imp}\] \[\hat u_\text{aln} = [\hat v^\mathcal B_{plf, xy}, -\hat v^\mathcal B_{body. xy}, \hat \omega^\mathcal B_{plf, z}, -\omega^\mathcal B_{body, z}]\]

explicit system parameter는 원래 값을 추정하는데, implicit system parameter의 경우에는 원래 값을 추정하는게 아니라 encoder를 통과한 이후의 latent vector를 예측 대상으로 합니다. 아무튼 explicit system paramter를 예측하게 되면 alignment command의 세 요소를 얻을 수 있게 되고, 남은 몸체 회전 각속도의 경우 IMU 센서를 통해 구할 수 있으므로, 모든 요소를 알게 됩니다.

\[L_{\mathrm{MSE}}^{\mathrm{exp}} = \bigl\|\hat{x}^{\mathrm{exp}} - x^{\mathrm{exp}}\bigr\|_2^2\] \[L_{\mathrm{MSE}}^{\mathrm{imp}} = \bigl\|\hat{\ell}^{\mathrm{imp}} - \mathrm{sg}\bigl[\ell^{\mathrm{imp}}\bigr]\bigr\|_2^2 \;+\; \lambda \,\bigl\|\mathrm{sg}\bigl[\hat{\ell}^{\mathrm{imp}}\bigr] - \ell^{\mathrm{imp}}\bigr\|_2^2\]

각각의 추정기는 위의 손실함수로 학습됩니다.

Reward function

위는 강화학습 모델에게 사용되는 보상들의 종류입니다.

• 0번 태스크 보상: 로봇의 몸체가 플랫폼에 부딪힌 경우 음수 보상을 부여해 안정적으로 서있도록 하는 역할
• 1번 태스크 보상: 플랫폼 좌표계 상에서 로봇 몸체가 중심과 가까운 만큼 보상을 부여해 최대한 중심에 머무르도록 하는 역할
• 2번 태스크 보상: 로봇과 플랫폼의 모션이 동일한 만큼 보상을 부여해 플랫폼과 동일하게 운동하게 하는 역할
• 3번 태스크 보상: 몸체의 기울기를 줄이는 역할

• 4번 태스크 보상: 로봇이 플랫폼 좌표계 상에서 일정한 높이를 유지하도록 해, 바닥에 딱 붙어 버티는 전략을 선택하지 못하도록 함

• 0, 1번 규제 보상: 관절 토크의 변화량과 그 자체의 크기, 속도, 가속도, 그리고 행동 변화가 급격하지 않도록 하는 역할
• 2번 규제 보상: 힘 소비를 줄이는 역할
• 3번 규제 보상: 로봇 발이 플랫폼으로 부터 받는 접촉력이 너무 크지 않도록 제한하는 역할
• 4, 5번 규제 보상: 로봇이 플랫폼에서 발을 자주 떼지 않도록 제한하는 역할
• 6번 규제 보상: 발이 미끄러지지 않도록 제한하는 역할

Training Environments

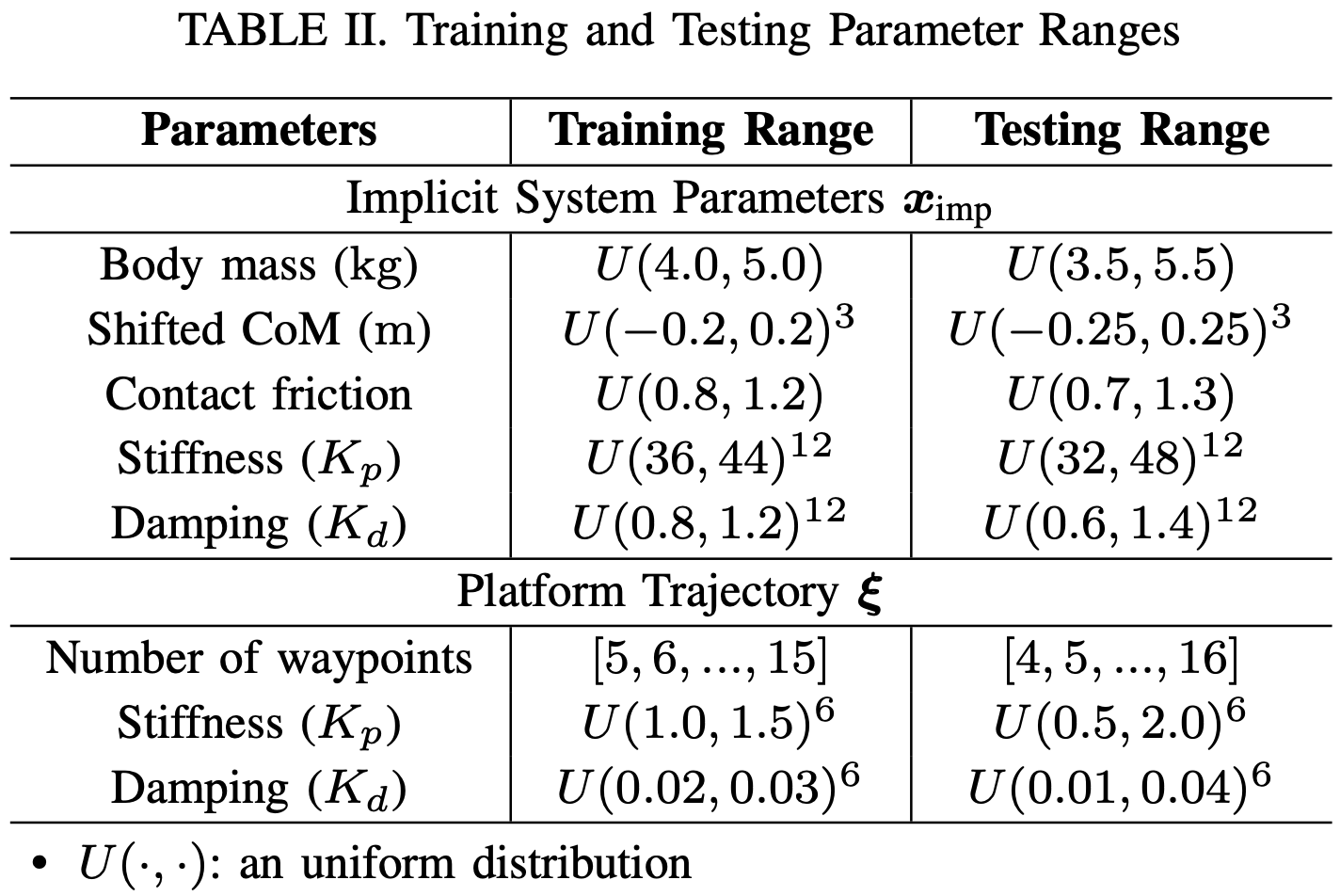
먼저 implicit system parameters는 위와 같은 범위에서 랜덤으로 결정됩니다. 로봇이 따라가야할 경로는 B 스플라인 기법을 통해서 생성됩니다. 위와 같이 점의 개수와 PD 제어의 계수를 다양한 값으로 설정해 플랫폼의 움직이 보다 다양하게 수집될 수 있도록 해줍니다.

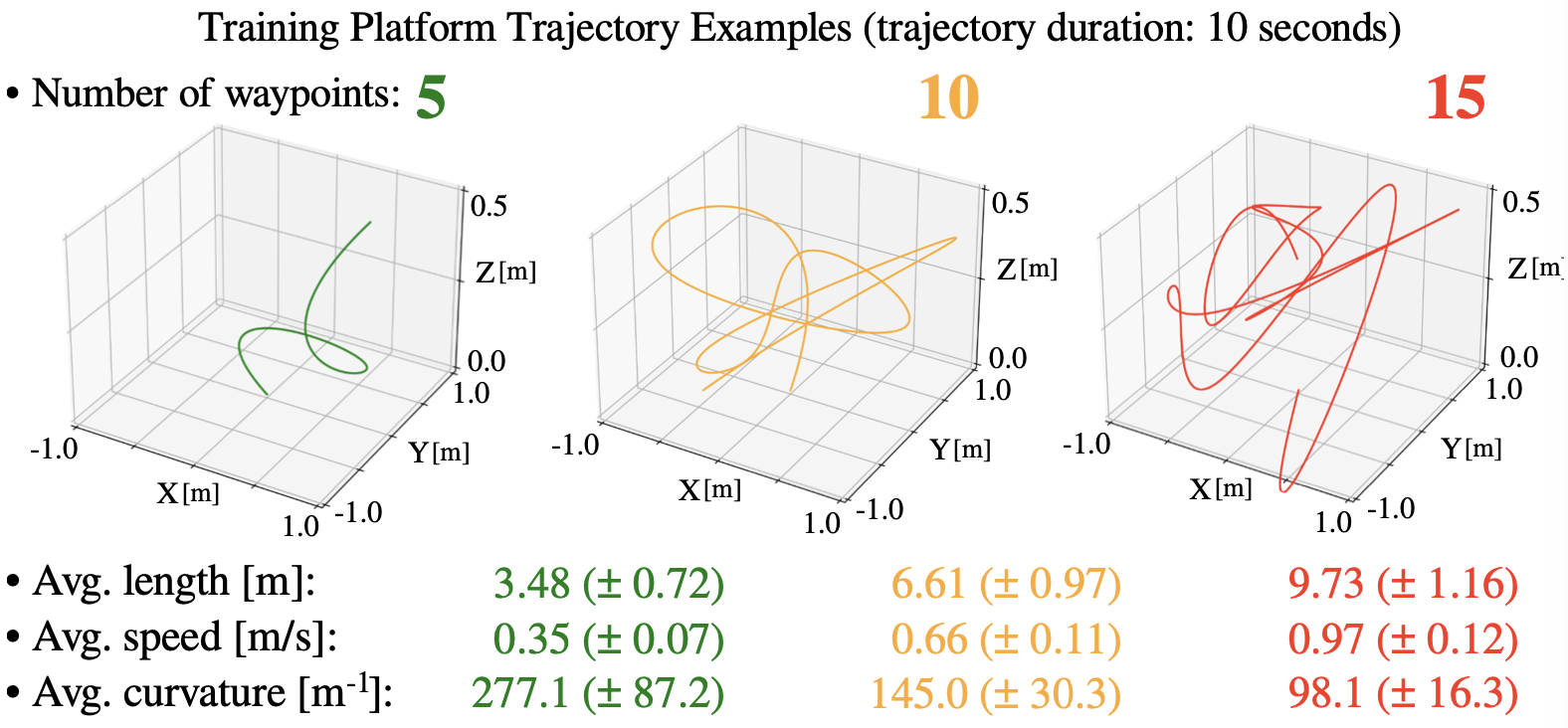
에피소드의 총 길이는 10초이며, 점의 개수가 많을 수록 난이도가 상승하게됩니다. 먼저 점의 개수가 작은 문제를 처음에 학습하고, 이후에 점점 난이도를 올려나갑니다.

강화학습 알고리즘으로는 ROA를 사용하는 PPO를 선택했으며, Actor backbone은 4층 MLP, Encoder는 2층 MLP로 설정되었습니다. explicit, implicit 추정기로는 2층의 1차원 CNN과 1층의 MLP가 선택되었습니다. 강화학습 에이전트는 backbone의 행동 출력을 그대로 사용하는 것이 아니라 가우시안 분포의 평균으로 사용되고, 분포의 표준편차로 학습 가능한 12차원 벡터를 설정해서 에이전트가 다양한 경우에 대해 탐색을 수행할 수 있도록 해줍니다. 보상함수에 사용되는 계수들은 경험적으로 가장 좋았던 값으로 선택되었습니다.

Isaac Gym 환경에서 8,192개의 병렬 환경을 만들어 학습합니다. Unitree의 A1 모델이 채택되었으며 플랫폼의 크기는 가로세로 2m에 두께는 20cm입니다. 총 4000번의 iteration을 수행했고 각 iteration은 0.24초의 분량으로 끊어서 학습됩니다. 학습 사양은 i9-9900K CPU와 RTX 4090 GPU 입니다.

Experimental Results

LAS-MP의 성능을 확인하기 위해 기존의 baseline 방법론들과 비교를 수행합니다. 그리고 평가를 할 때에, 학습할 때 사용한 범위보다 넓은 범위에서 플랫폼 움직임을 생성해 일반화 능력을 평가할 수 있도록 합니다. 그리고 LAS-MP에서 사용한 explicit estimators와 alignment commands 부분을 제거해 해당 기능들이 정말로 모델 성능에 긍정적인 영향을 미치는지 확인합니다.

Evaluation of Balancing Performance

학습시 보다 더 넓은 범위에서 10,000개 플랫폼 경로를 생성하고 이를 바탕으로 평가합니다. 그리고 총 1,024개의 4족보행 로봇들을 만들고, 각각 로봇의 intrinsic properties는 다르게 설정해 다양한 환경에서 강건하게 대응할 수 있는지 평가합니다.

위는 로봇이 대응해야 하는 플랫폼의 움직임 예시인데, 벤치마크 데이터셋은 평균 길이 7.12 m에 평균 속도 0.69 m/s, 그리고 평균 곡률은 132.6 m$^{-1}$로 구성됩니다.

다양한 베이스라인 방법론들과 비교했을 때, LAS-MP가 대부분의 경우에서 가장 좋은 성능을 보여줍니다. 전력은 Stand Still이 가장 적게 사용하기는 하지만, 충돌 확률이 LAS-MP와 비교했을 때 크게 차이납니다.

Ablation Study

정렬 명령, explicit extimator 등등의 기능들을 네 가지 조합으로 제거했을 때의 성능을 측정해 봤는데, 모든 경우에서 제거하기 이전 보다 훨씬 낮은 성능을 보여줍니다.

Analysis of State Estimators

위는 추정기와 실제 값 차이의 오차입니다. 평균적으로 매우 작은 오차 내에서 적절한 예측이 수행됨을 확인할 수 있습니다.

Conclusion

LAS-MP는 6자유도 플랫폼 움직임에 대응할 수 있는 최초의 방법론이라는 점에서 의의가 있습니다. 그러나 즉각적인 정렬 명령에 따라 정렬하기 때문에 꾸준히 발생하는 오류를 바로잡기 어렵다는 문제가 있습니다. 이를 해결하기 위해 플랫폼의 중심점을 추가로 localize해 전역적으로 발생하는 오류를 해결하는 것을 향후 연구 방향으로 제시하고 있습니다.