HumanMimic: Learning Natural Locomotion and Transitions for Humanoid Robot via Wasserstein Adversarial Imitation

이 포스팅은 ‘HumanMimic: Learning Natural Locomotion and Transitions for Humanoid Robot via Wasserstein Adversarial Imitation‘에 대한 내용을 담고 있습니다.

논문 주소: https://arxiv.org/abs/2309.14225

HumanMimic: Learning Natural Locomotion and Transitions for Humanoid Robot via Wasserstein Adversarial Imitation

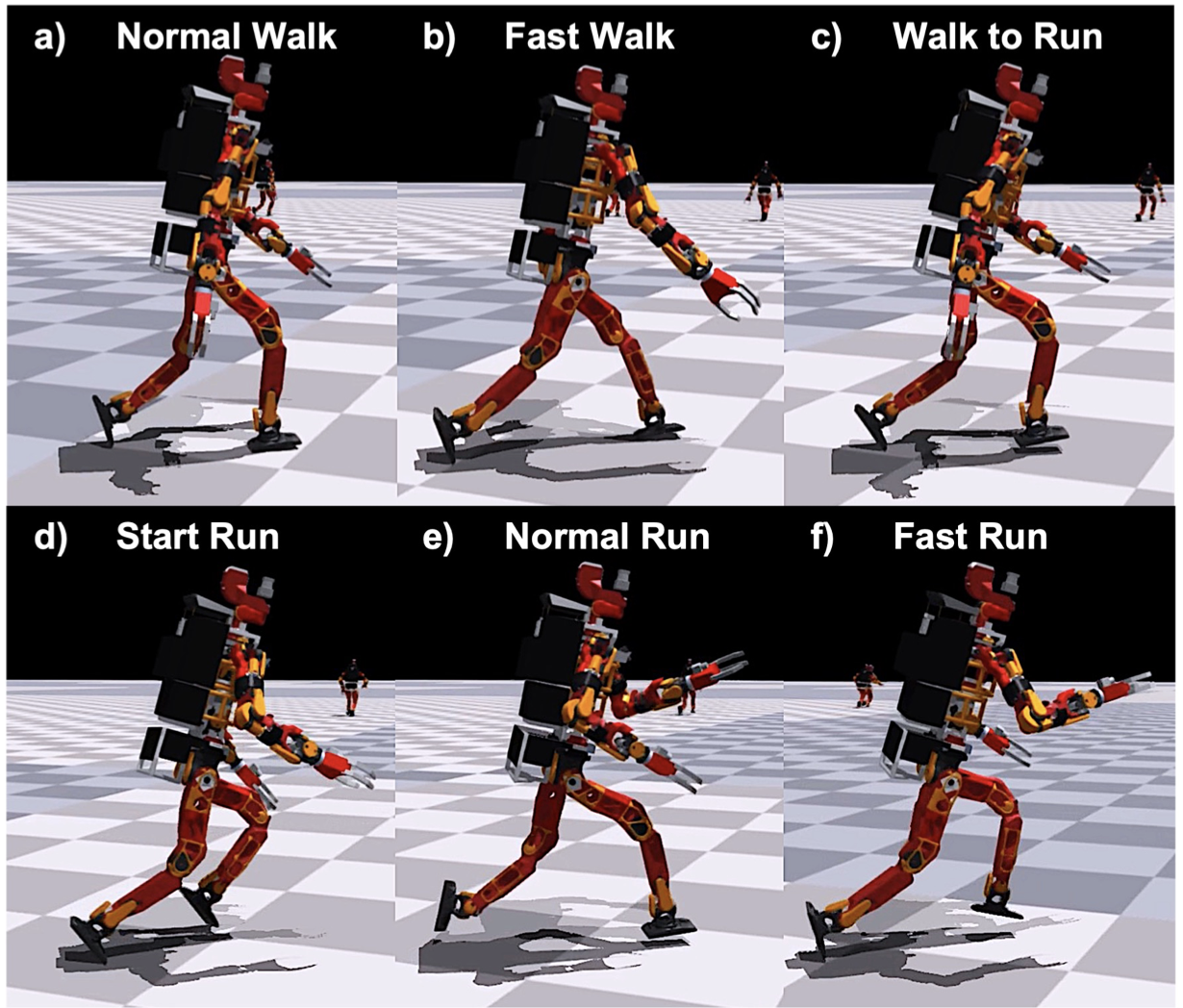
사람은 굉장히 다양한 이동 행동을 수행하고, 속도 변화, 외부 방해에도 적절히 대응하면서 걸음걸이 패턴을 전환할 수 있는 능력이 있습니다. 사람이 보여주는 이러한 자연스러운 걸음걸이 패턴을 로봇에 구현하는 것은 휴머노이드 로봇의 본질적인 복잡성으로 인해 굉장히 어려운 문제입니다. 단순한 모델이나 최적 제어를 통해 이를 구현해보려는 시도가 있었지만, 애초에 액추에이터가 부족한데 그마저도 복잡해서 자연스러운 움직임을 보여주지는 못했습니다. 그 대안으로 심층 강화학습을 통해 모델링 과정을 반자동화해 해결하려는 방향이 최근에 많이 시도되고 있고 꽤나 성공적으로 보여집니다. 그럼에도 복잡한 휴머노이드 로봇에서는 바람직하지 못한 전신 행동, 팔 스윙, 부자연스러운 걸음걸이 등등이 나타납니다. 이런 문제점을 해결하기 위해 휴리스틱을 설정하거나 정교한 보상 설계를 통해 자연스러운 걸음걸이를 학습하도록하는 시도들이 있었지만, 사람의 자연스러운 걸음걸이 패턴을 표현하는 것 부터가 어려운 일입니다.

위의 문제점들을 해결하기 위해 특별한 보상 함수를 설계하지 않고, 인간 시연자의 걸음걸이 데이터를 제공해서 이를 따라하도록 학습시키는 방법론이 사용됩니다. 구체적으로는 판별기(Discriminator)를 생성해서 현재 로봇의 행동과 인간 시연자의 걸음걸이와 비교 구분시키고, 이를 보상으로 제공하는 AMP(Adversarial Motion Prior) 방법론이 있습니다. 그런데 AMP에서 사용하는 판별기는 BCE Loss 혹은 LS Loss로 학습되는데요, 고차원 공간에서 확률 분포가 겹치지 않는 경우에는 위 손실함수를 사용했을 때 학습이 제대로 수행되지 못하고 붕괴되는 경우가 더러 발생합니다. 특히 현재 논문에서 다루는 휴머노이드 로봇은 굉장히 많은 관절으로 구성되어 있기 때문에, 더더욱 확률 분포가 겹치지 않는 경우가 많습니다. 이 문제를 해결하기 위해서 논문에서는 Wasserstein Distance를 도입해 두 분포 사이의 거리를 보다 적절하게 측정할 수 있도록 해줍니다.

Motion Retargeting

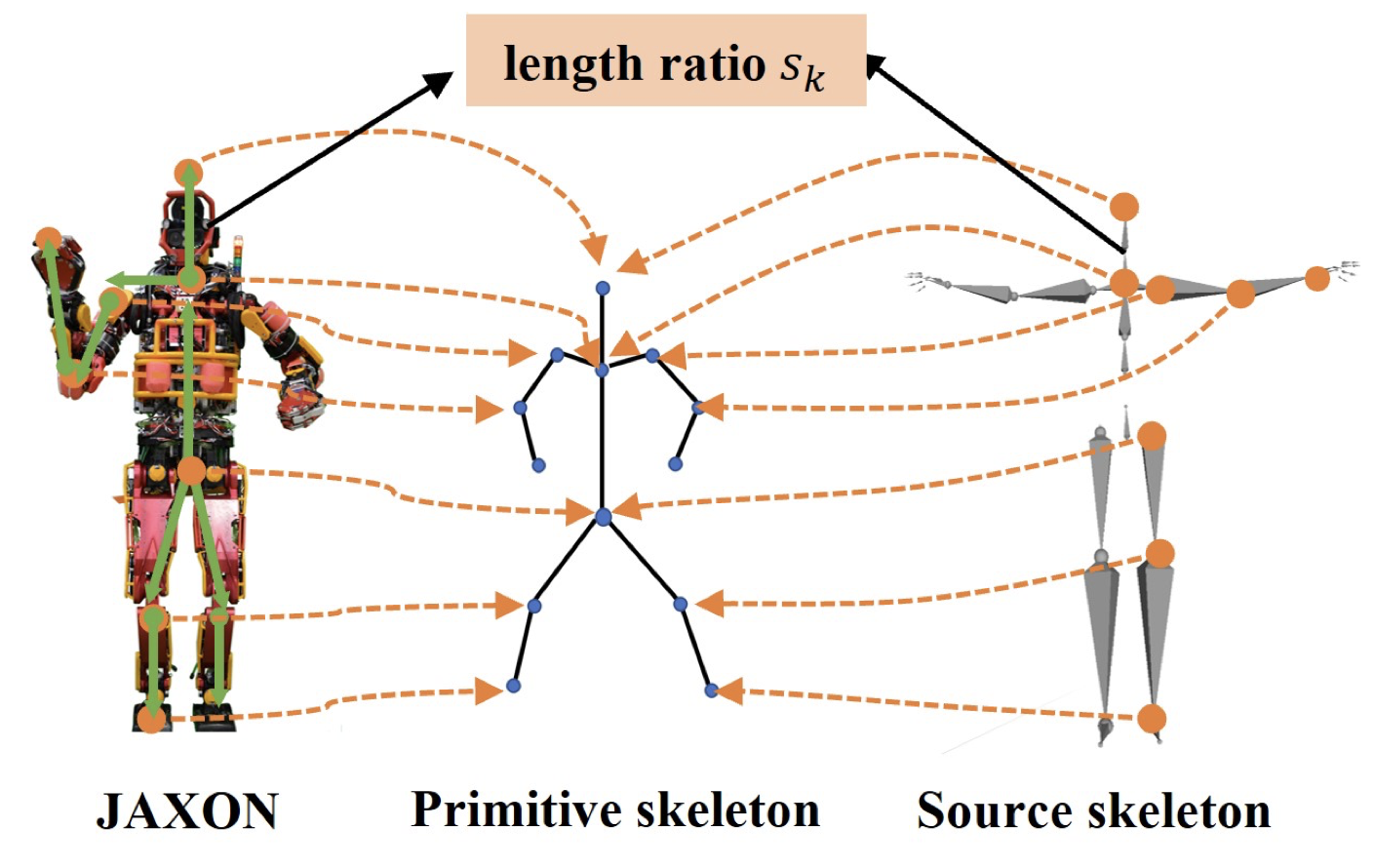
모델 안에 선언된 판별기는 인간의 걸음걸이 데이터와 이 논문에서 사용한 JAXON 로봇의 걸음걸이를 비교해서, 인간의 걸음걸이인지, 로봇의 걸음걸이인지를 분류합니다. 그런데 일단 비교를 하려면 동일한 형태로 데이터로 맞춰줘야 합니다. 따라서 인간 걸음걸이 데이터와 JAXON의 형태를 Primitive Skeleton으로 추상화시킨 다음 두 데이터를 동일한 형태로 정렬시켜줍니다.

\[L' = \{l'_{ij}\}\] \[M'_s = \{m'_t \mid t \in \{1, ..., T\} \}\] \[m'_t = ({^w}P'_r, {^w}R'_r, {^0}R'_1,..., {^{j-1} }R'_j)\]

MoCap 데이터는 링크들의 길이, 시간에 따른 움직임을 나타내는 변환 행렬으로 구성되어 있습니다. 루트 조인트 기준으로 해서 계층적으로 퍼져나가면서 구할 수 있도록 주어지는데, 위의 정보들을 사용해서 모든 키 조인트들의 월드 좌표계에 대한 동차 변환 행렬을 구할 수 있습니다.

\[S = \{s_k \mid k \in \{1, ..., n\}\}\] \[\overrightarrow r'_k = {^w}P'_k - {^w}P'_{k-1}\] \[\overrightarrow r_k = s_k \cdot \overrightarrow r'_k\]

MoCap 데이터의 링크 길이들과 JAXON 로봇의 링크 길이 비율 차이를 보완해주면, MoCap 데이터의 움직임을 JAXON의 형태에 맞춰줄 수 있게 됩니다.

\[C_1 = \sum_k\left\| {^r} P_k - p_k(\theta) \right\|^2 \quad \text{: position goal for key joints}\] \[C_2 = \sum_e\left\| {^r} P_e - p_e(\theta) \right\|^2 \quad \text{: pose goal for end-effectors}\] \[C_3 = \left\| \theta_t - \theta_{t-1} \right\|^2 \quad \text{: minimal displacement goal}\] \[C = \text{argmin}_\theta \sum_i \kappa_i C_i(\theta)\]

로봇의 움직임과 MoCap 데이터의 움직임을 비교할 때, 각 관절의 좌표와 방위를 보고 판별하지 않고 로봇의 관절값을 보고 바로 구분을 시킬 것이기 때문에 역기구학을 통해 로봇의 관절값을 찾아줍니다. 이때 기하학적으로 역기구학을 계산하지 않고 위의 세 가지 목적함수를 사용해 기울기 기반의 최적화 방법을 사용해 구합니다.

\[\theta_{\text{min}} \leq \theta_t \leq \theta_{\text{max}}\] \[\dot \theta_{\text{min}} \leq \frac{\theta_t - \theta_{t-1}}{\Delta t} \leq\dot \theta_{\text{max}}\]

이때 위의 제약사항들을 고려해 관절 위치와 관절 속도의 한계를 고려합니다.

Wasserstein Adversarial Imitation

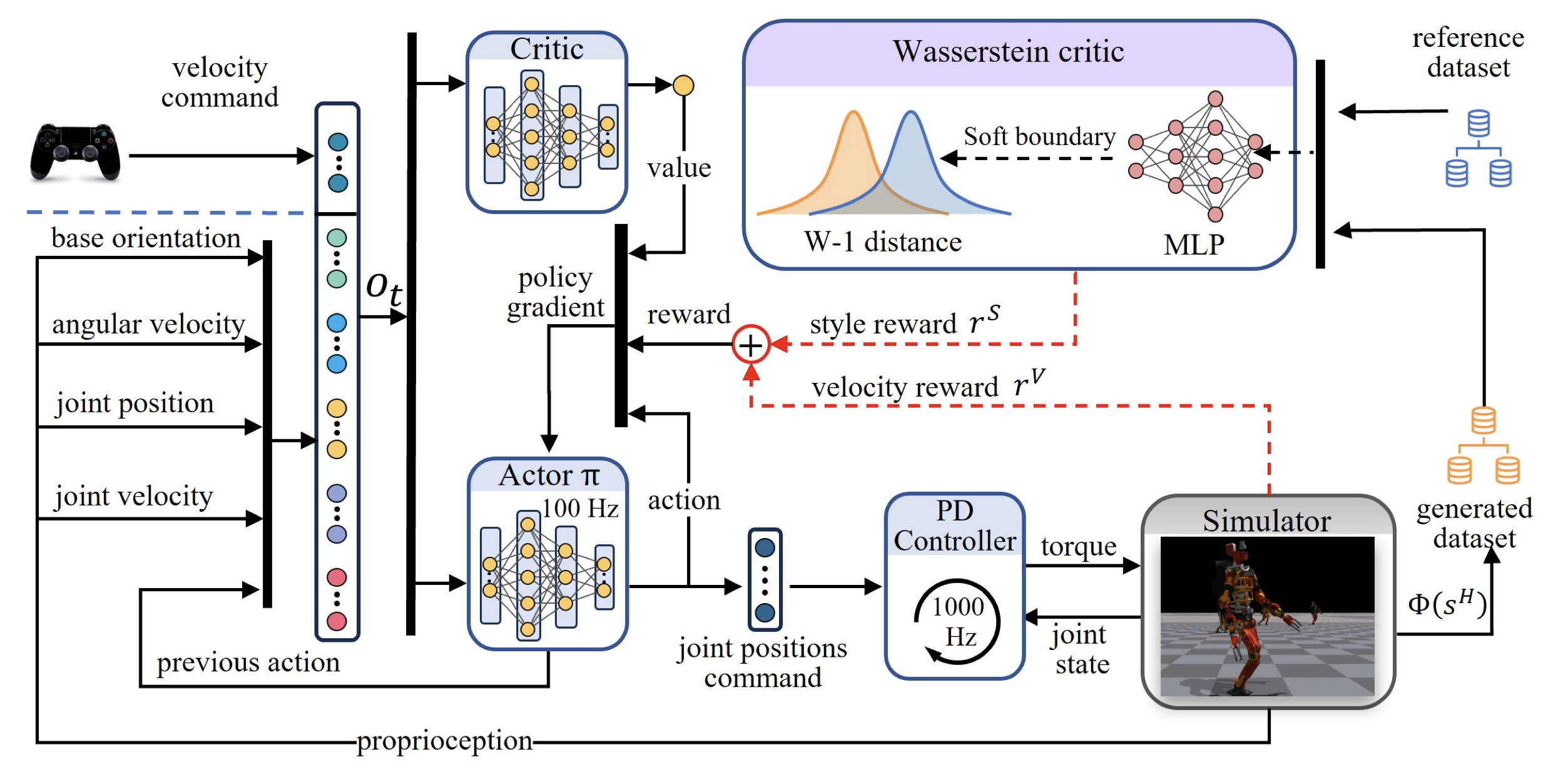
위는 Wasserstein Adversarial Imitation Learning Framework의 전체 도식입니다. 액터 크리틱 네트워크와 Wasserstein critic, 그리고 직접적인 제어는 PD 컨트롤러로 수행됩니다.

Velocity-Conditioned Reinforcement Learning

강화학습 에이전트는 로봇이 지정한 속도에 따라 자연스럽게 움직이고 있는가에 대해 보상 신호를 획득합니다.

\[r_t = \mu_1r^V + \mu_2r^S\] \[r^V = \beta_1 \exp(-\frac{||v^*_{xy} - v_{xy}||^2}{\lambda_l|v^*_{xy}|}) + \beta_2 \exp(-\frac{||w^*_{z} - w_{z}||^2}{\lambda_h|w^*_{z}|})\] \[r^S \text{: Style Reward}\]

지정한 속도에 따라 로봇이 잘 움직이고 있는가는 로봇의 CoM의 속도를 기준으로 측정합니다. CoM의 선속도와 각속도를 정규화한 값에 가중치를 가해 고려 비율을 결정합니다. 그리고 로봇이 자연스럽게 움직이고 있는가는 Style Reward라고 Wasserstein Distance를 통해 구하게 되는데, 이 내용은 아래에서 자세하게 살펴봅니다.

Wasserstein Critic

기존의 GAIL에서는 판별기를 학습시킬 때 BCE Loss를 사용합니다. BCE Loss를 사용한다는 것은 Jensen-Shannon Divergence를 최소화 하는 것과 비슷한데요, 문제는 두 분포가 겹치지 않을 때 기울기 소실이나 불안정한 학습, 그리고 모델 붕괴가 나타난다는 점에 있습니다. 예를 들어, 두 분포가 상당히 멀리 떨어져 있는 경우 판별기는 굉장히 빠르게 두 분포를 구별할 수 있도록 학습됩니다. 그런데 판별기가 의미있는 기울기를 제공하기 위해서는 조금이라도 원래 분포와 가까운 생성 데이터에 대해 이게 좀 더 낫다고 판별기가 판단해주어야 하는데, 너무 이르게 판별기가 학습되면 실제 데이터와 더 가깝게 만들어진 생성 데이터에 대해 유의미한 차이를 반환하지 않기 때문에 기울기 소실 문제가 발생합니다.

\[\Gamma_\mathcal F(\mathcal P,\mathcal Q) := \sup_{f \in \mathcal F} \left| \int_\mathcal M f d\mathcal P - \int_\mathcal M f d\mathcal Q \right|\] \[\mathcal F = \{f : ||f||_L \leq 1\}\]

이러한 문제점을 해결하기 위해서 저자들은 IPM(Integral Probabilistic Metric)을 사용합니다. IPM은 위의 수식으로 두 확률 분포의 차이를 측정하는 메트릭인데, 직관적으로는 두 확률분포의 기댓값의 차이를 가장 크게 만들어주는 함수를 선택했을 때의 그 차이 값을 의미합니다. 이때 사용하는 함수의 Lipschitz 상수(함수의 최대 기울기)가 1보다 작은 경우 IPM은 Wasserstein-1 Distance와 쌍대 표현이 됩니다.

\[\arg\min_\theta - \mathbb{E}_{x \sim P_r}[D_\theta(x)] + \mathbb{E}_{\tilde{x} \sim P_g}[D_\theta(\tilde{x})] + \lambda \mathbb{E}_{\hat{x} \sim P_{\hat{x}}}[(\|\nabla_{\hat{x}}D_\theta(\hat{x})\|_2 - 1)^2]\] \[D_\theta(x) \quad\text{: Wasserstein critic}\] \[\hat x = \alpha x + (1 - \alpha)\tilde x \quad \text{: interpolated samples}\]

위의 Wasserstein-1 Distance를 기댓값의 형태로 적으면 위와 같은 수식이 됩니다. 가장 마지막에 기울기 규제 항이 새롭게 늘어가게 되는데, 이 부분은 Critic이 Lipschitz-1 조건을 만족하도록 제약하는 역할을 해줍니다. 그러니까 우리가 사용하는 신경망이 Lipschitz를 만족하기 어렵기 때문에 규제항을 통해 기울기 노름이 1로 가까워지도록 유도하는 것입니다.

\[\arg \min_\theta - \mathbb{E}_{x \sim P_r}[\tanh(\eta D_\theta(x))] + \mathbb{E}_{\tilde{x} \sim P_g}[\tanh(\eta D_\theta(\tilde{x}))] + \lambda \mathbb{E}_{\hat{x} \sim P_{\hat{x}}}[(\max\{0, \|\nabla_{\hat{x}}D_\theta(\hat{x})\|_2 - 1\})^2]\] \[r^S = e^{D_\theta(\tilde x)}\]

Wasserstein critic으로 신경망을 사용하는데, 신경망은 출력 값의 범위가 제한되지 않기 때문에 초기 불안정한 학습의 결과 극단적인 음수 값으로 수렴해버리는 경우가 더러 발생합니다. 이를 방지하기 위해 Wasserstein critic의 출력값에 $\eta$를 곱하고 Hyperbolic Tangent를 씌워 출력을 -1부터 1 사이의 값으로 제한합니다. 그리고 Wasserstein critic의 기울기 노름이 1 이하일 때에는 패널티를 부과하지 않음으로써 더 안정적인 학습이 이루어지도록 합니다. 그렇게 학습된 Wasserstein critic로 위의 Style reward를 위와 같이 디자인해 사용합니다.

Experiment

실험 로봇으로는 휴머노이드 로봇 JAXON을 사용합니다. Isaac Gym 환경을 사용하고, NVIDIA 3090Ti를 통해 총 30시간동안 학습됩니다. Actor와 Critic, 그리고 Wasserstein Critic은 모두 동일한 MLP 구조를 사용합니다. Actor-Critic은 총 102차원의 벡터를 입력으로 받고, Wasserstein Critic은 78차원의 벡터를 입력으로 받습니다. 구체적인 관측 벡터 구성은 논문에서 확인할 수 있습니다.

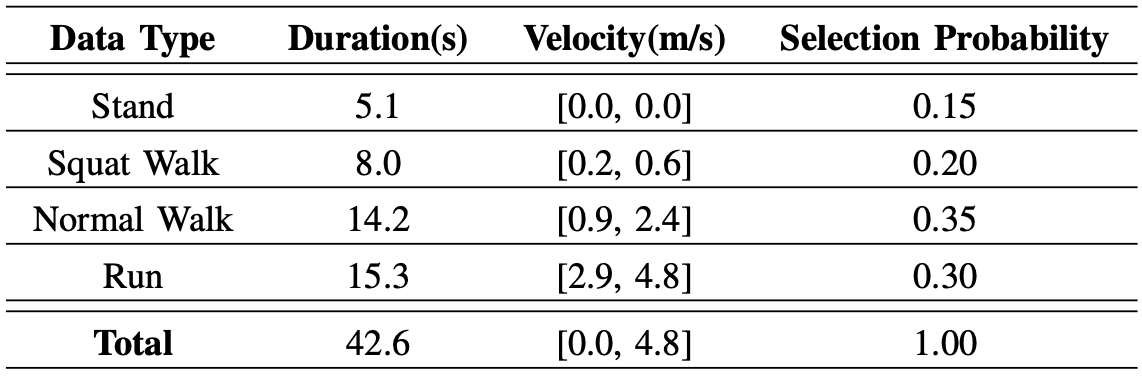
모션 데이터로는 CMU-MoCap과 SFU-MoCap 데이터가 사용되었으며, 그 외에 가만히 서있는 모션은 직접 디자인되었고 스쿼트 자세로 걸어가는 모션은 기존 로봇 컨트롤러를 사용해 기록되었습니다.

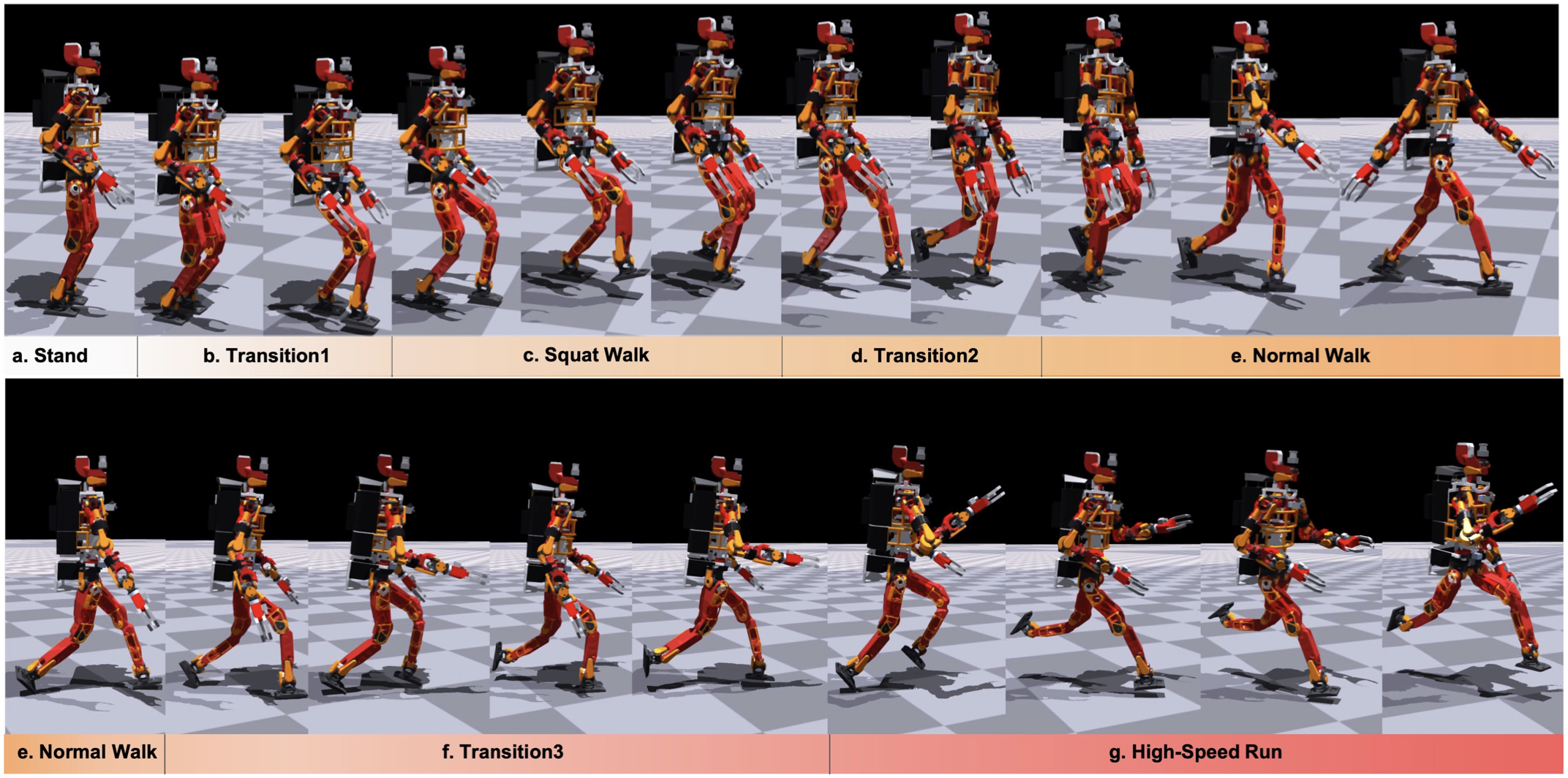
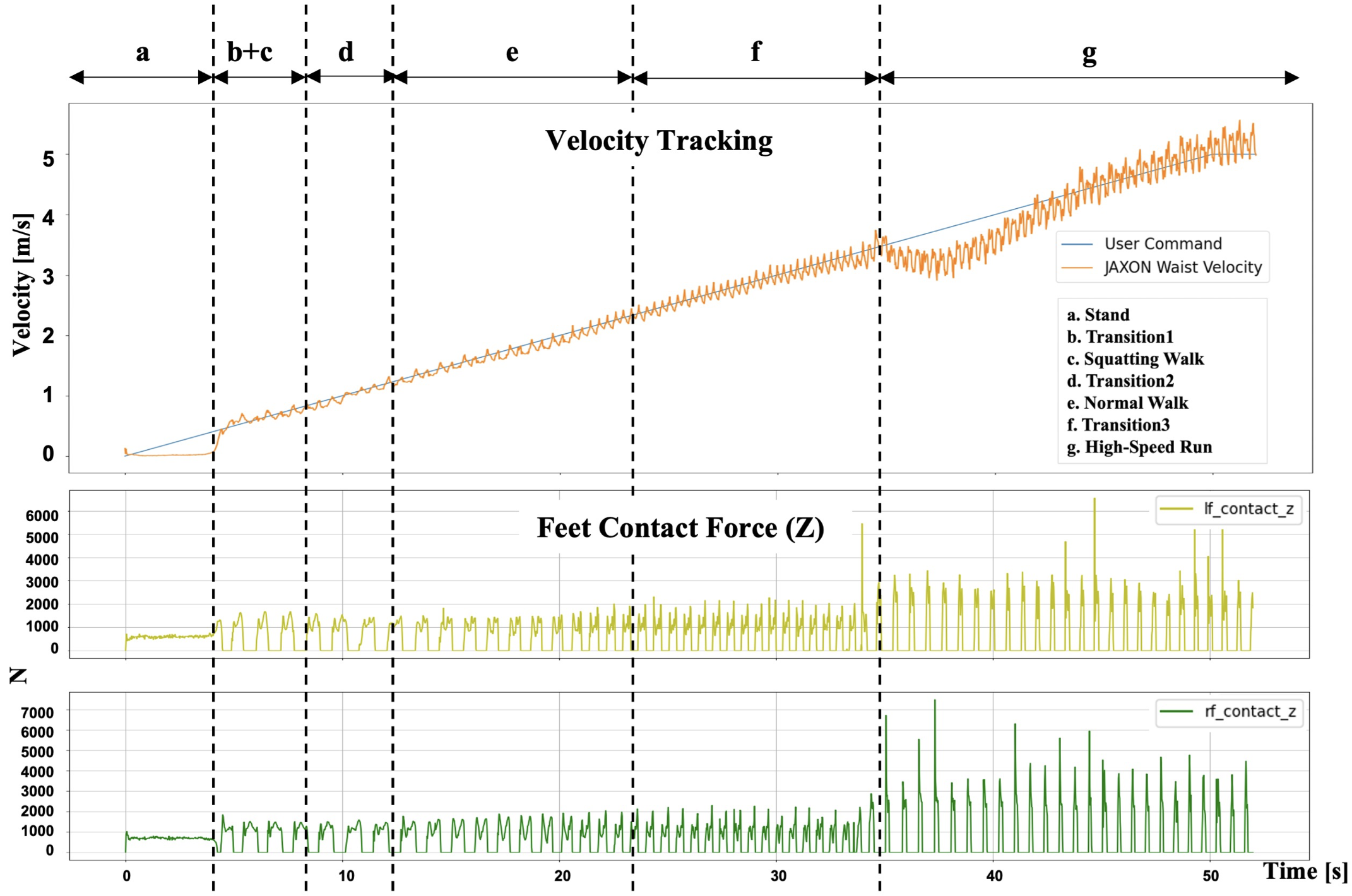
먼저 서 있는 상태에서 달리기까지 자연스럽게 전환할 수 있는 능력을 테스트합니다. 요구하는 속도를 높임에 따라 로봇이 성공적으로 동작을 전환하는 것을 확인할 수 있습니다. 참조 데이터셋에 전환 동작이 포함되어있지 않음에도 불구하고 자연스럽게 동작을 전환합니다. 속도가 점차 높아짐에 따라 양발이 모두 바닥에서 떨어지는 air phase도 확인할 수 있습니다.

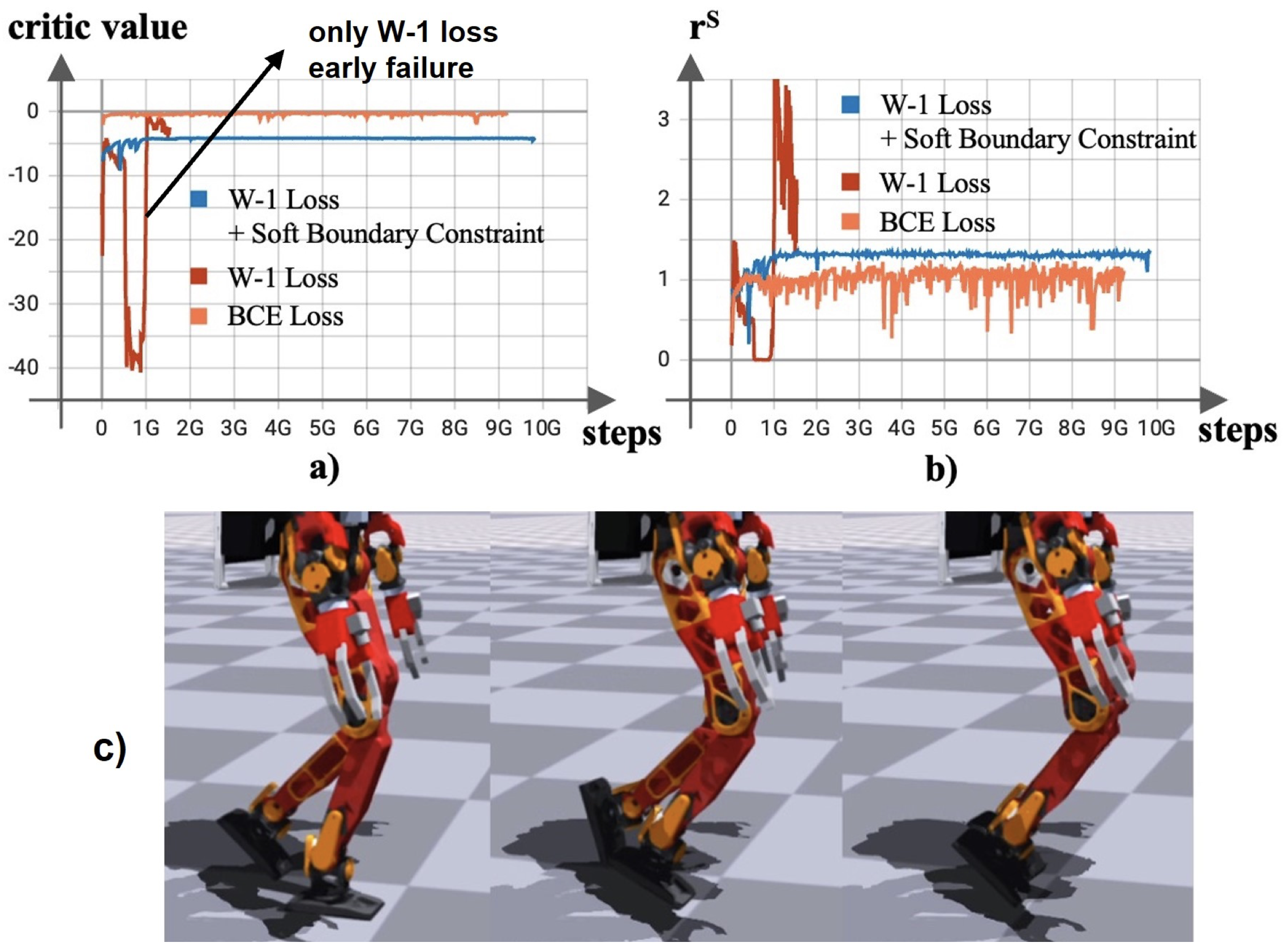
다음으로 Wasserstein Loss를 효과를 검증하기 위해, 기존의 BCE Loss를 사용한 경우, 그리고 Wasserstein을 사용하기는 하지만 Soft Boundary Constraint를 사용하지 않는 경우의 성능이 어떻게 차이나는지 살펴봅니다. BCE를 사용한 경우 판별자의 출력이 0과 1 사이의 값으로 결정됩니다. 그러나 논문에서 제시한 방법과 비교했을 때, 변동성이 상대적으로 더 크고 스타일 보상에도 불안정한 변화가 발생합니다. Soft Boundart가 없는 Wasserstein의 경우 판별자의 출력이 매우 넓은 범위에서 요동쳐 학습이 실패하게 됩니다. 논문에서 제시한 방법을 사용할 때, 가장 안정적으로 Critic value가 수렴하는 것을 확인할 수 있고, 그에 따른 스타일 보상 역시 안정적으로 유지되는 것을 확인할 수 있습니다.

마지막으로 Isaac Gym에서 학습한 모델이 다른 시뮬레이션 환경에서도 잘 동작하는지 확인합니다. 논문에서는 Choreonoid라고 Hrpsys라는 실시간 제어 소프트웨어와 통합되어있고, high-fidelity 환경으로 현실 세계와의 차이가 적은 시뮬레이터입니다. 이 환경에서 Push-recovery와 Blind Stair-Climbing 태스크에 대해 테스트했는데, 두 가지 태스크에서 모두 성공적으로 수행함을 확인했습니다.

Conclusion

HumanMimic에서는 Wasserstein adversarial imitation learning에 Soft Boundary 제약을 더해 학습 안정성을 높임으로써 다양한 인간 시연 데이터를 효과적으로 학습시킵니다. 이를 통해 학습 데이터로 제공되지 않은 걸음걸이 모드를 전환할 수 있었고 그 외의 다른 태스크들에서도 성공적으로 해결할 수 있음을 실험을 통해 보여줍니다. 향후 연구로 실제 로봇에 적용해 좀 더 다목적적이고 자연스러우면서도 동적인 휴머노이드 보행을 구현하는 방향을 제시합니다.