Graph-based 3D Collision-distance Extimation Network with Probabilistic Graph Rewiring

이 포스팅은 ‘Graph-based 3D Collision-distance Extimation Network with Probabilistic Graph Rewiring‘에 대한 내용을 담고 있습니다.

논문 주소: https://arxiv.org/pdf/2310.04044

Graph-based 3D Collision-distance Extimation Network with Probabilistic Graph Rewiring

로봇에게 충돌을 감지할 수 있는 능력은 사고 방지를 위해 매우 중요합니다. 이 논문에서는 두 물체 사이의 최소거리를 추정해 충돌을 방지하는 방법론을 소개합니다. 두 물체 사이의 최소거리를 추정하는 가장 전통적인 iterative한 방법으로는 GJK(Gilbert-Johnson-Keerthi)가 있습니다. Convex한 두 물체 사이의 거리를 추정할 때 매우 유용한 도구이긴 하지만, 복잡한 기하학적 물체 사이의 거리를 추정할 때 적용하기 어렵다는 문제점이 있습니다. 다른 방법으로 Data-driven distance estimation 방법론이 있습니다. 이 방법론에서는 다양한 학습 및 최적화 방법론들을 사용해 두 물체 사이의 거리를 추정하는데, 가장 전형적으로는 point cloud를 사용합니다. 그런데 단순히 점을 기반으로 표면을 표현하면 convex하지 않은 물체에 대해서 부정확한 거리를 추정할 수 있고, 새로운 환경에 대한 일반화 능력도 떨어진다는 단점이 있습니다. 또 다른 방법으로 SDFs(Signed Distance Fields)를 사용하는 접근이 있지만, 역시 일반화 능력이 떨어지고 학습할 때 비용이 굉장히 높다는 단점이 있습니다.

이러한 기존의 방법론들의 문제점들을 해결하기 위해, 이 논문의 저자는 이전에 GNN 기반의 해결책(GDN)을 제시했습니다. 두 물체마다 각각 표면을 따라 그래프를 만들고 이를 사용해 두 물체 사이의 거리를 어텐션 매커니즘을 통해 추정했는데요, 그래프를 사용해 물체의 거리를 추정하는 방법 자체가 계산량을 많이 필요로 해서, 2D 이상으로는 적용하기 어렵다는 문제점이 있었습니다.

이 문제를 해결하기 위해서 기존의 방법론을 보완한 GDN-R(Rewiring)을 제안합니다. 두 그래프를 입력으로 받은 다음 여러 MPNN(Message-Passing Neural Network)를 통과시킨 뒤, 가장 높은 연결성을 갖는 노드들을 선정하는 Rewiring 단계를 거칩니다. 마지막으로 Gumble noise로 무작위성을 추가해 다양한 물체에 대한 일반화 능력을 갖출 수 있게 합니다.

Background

1-hop message passing을 하는 GNN에 대해 간단하게 설명합니다.

\[G = (\mathcal V, \mathcal E), \quad v_j \in \mathcal V, \quad e_{ij} \in \mathcal E\] \[x_i \in \mathbb R^{d_v}, \quad x_{ij} \in \mathbb R^{d_e}\]

먼저 그래프는 위와 같이 노드와 간선으로 구성됩니다. 그리고 각각의 노드와 간선에는 특징 벡터들이 부여되어 있습니다. MPNN의 각 레이어들을 거쳐가면서 노드들은 주변에 연결되어 있는 간선과 노드의 정보를 점점 통합해 쌓아나가게 됩니다.

\[m_{ij} = \phi(x_i^{(l)}, x_j^{(l)}, x_{ij}^{(l)})\]

먼저, 자신의 노드, 그리고 바로 연결된 다른 노드와 그 사이의 간선이 가지는 세 벡터들을 입력으로 받아 MLP를 통과시켜 얻은 새로운 특징 벡터를 Massage라고 정의합니다. 위 식은 노드 쌍 사이에서 메시지를 만들어내는 과정을 표현한 것인데, 그래프에 존재하는 모든 연결에 대해 위 과정을 수행해, 자신의 이웃 수 만큼의 메시지를 생성하게 됩니다.

\[\Box_{j: e_{ij} \in E} \phi\bigl(x_i^{(l)}, x_j^{(l)}, x_{ij}^{(l)}\bigr)\]

각 이웃으로부터 하나씩 얻은 메시지를 그냥 다 더하거나, 그 중에 가장 큰 값을 취하는 등의 연산을 통해 메시지를 통합합니다.

\[x_i^{(l+1)} = \gamma\bigl(x_i^{(l)}, M_i\bigr) = \gamma\left(x_i^{(l)}, \Box_{j: e_{ij} \in E} \phi\bigl(x_i^{(l)}, x_j^{(l)}, x_{ij}^{(l)}\bigr)\right)\]

그렇게 통합해 얻게 된 최종적인 메시지를 다시 원래 노드의 특징 벡터와 함께 또 다른 MLP에 통과시킵니다. 그리고 그 결과물이 노드의 특징 벡터로 업데이트됩니다.

Method: GDN-R

이제 GDN-R이 어떻게 동작하는지 아래에서 자세하게 살펴봅니다.

Initial Graph Construction

\[G^{o_1} = \bigl(\mathcal V^{o_1}, \mathcal E^{o_1}\bigr), \quad G^{o_2} = \bigl(\mathcal V^{o_2}, \mathcal E^{o_2}\bigr)\]

충돌할 가능성이 있는 두 물체별로 그래프를 생성합니다.

\[{x}_i^{(0)} = \bigl(p_i,\, {^{o_2} } p_i,\, c_{o_1}\bigr) \quad \text{where}\quad v_i \in V_{o_1}\] \[{x}_j^{(0)} = \bigl(p_j,\, {^{o_1} } p_j,\, c_{o_2}\bigr) \quad \text{where}\quad v_j \in V_{o_1}\]

노드는 특징으로 총 세 가지 원소를 가집니다.

• 3차원 전역 좌표
• 상대 물체의 중심 좌표계 기준의 3차원 좌표
• 물체의 클래스 정보 (0 또는 1)

\[x_{ij}^{(0)} = x_{i}^{(0)} - x_{j}^{(0)}\]

노드의 특징을 바탕으로, 정의된 간선의 특징을 두 노드 간의 차로 설정합니다. 노드 정보의 차를 통해 상대적 위치 관계, 거리, 클래스 정보를 간선이 가질 수 있도록 합니다.

이렇게 하고 나면 각각의 물체 그래프의 모든 노드와 간선에 대해 특징 벡터가 결정됩니다. 그런데 두 물체 그래프 사이에는 아직 어떤 연결도 없어서 두 그래프가 서로 정보를 주고 받을 수 없습니다. 따라서 두 그래프 사이를 연결해주는 새로운 그래프를 만들어줍니다.

\[G_{IE} = (\mathcal V_{IE}, \mathcal E_{IE})\]

위에 새롭게 정의한 그래프는, 동일한 노드 개수만큼씩 각 물체 그래프에서 선정됩니다. 선정되는 방식은 랜덤으로 할 수도 있고, 아니면 충돌할 가능성이 높은 노드들에 대한 정보를 사용해 선정할 수도 있습니다. 아무튼 그렇게 뽑은 노드들이 있는 그래프에 간선을 정의하는데요, 여기에서 오직 다른 물체에 속하는 노드 사이에서만 간선이 생성됩니다. 간선 특징의 초기화는 마찬가지로 노드 특징의 차로 수행됩니다.

\[G = G_{o_1} \cup G_{o_2} \cup G_{IE}\]

그리고 위 세 개의 그래프를 모두 합쳐서 사용하게 됩니다

​

\[{x}_i^{(l+1)} = \sum_{j \in \mathcal{N}_G(i)} h_\theta^{(l)}\Bigl( {x}_i^{(l)},\, {x}_j^{(l)},\, {x}_{ij}^{(l)} \Bigr) \tag{3}\]

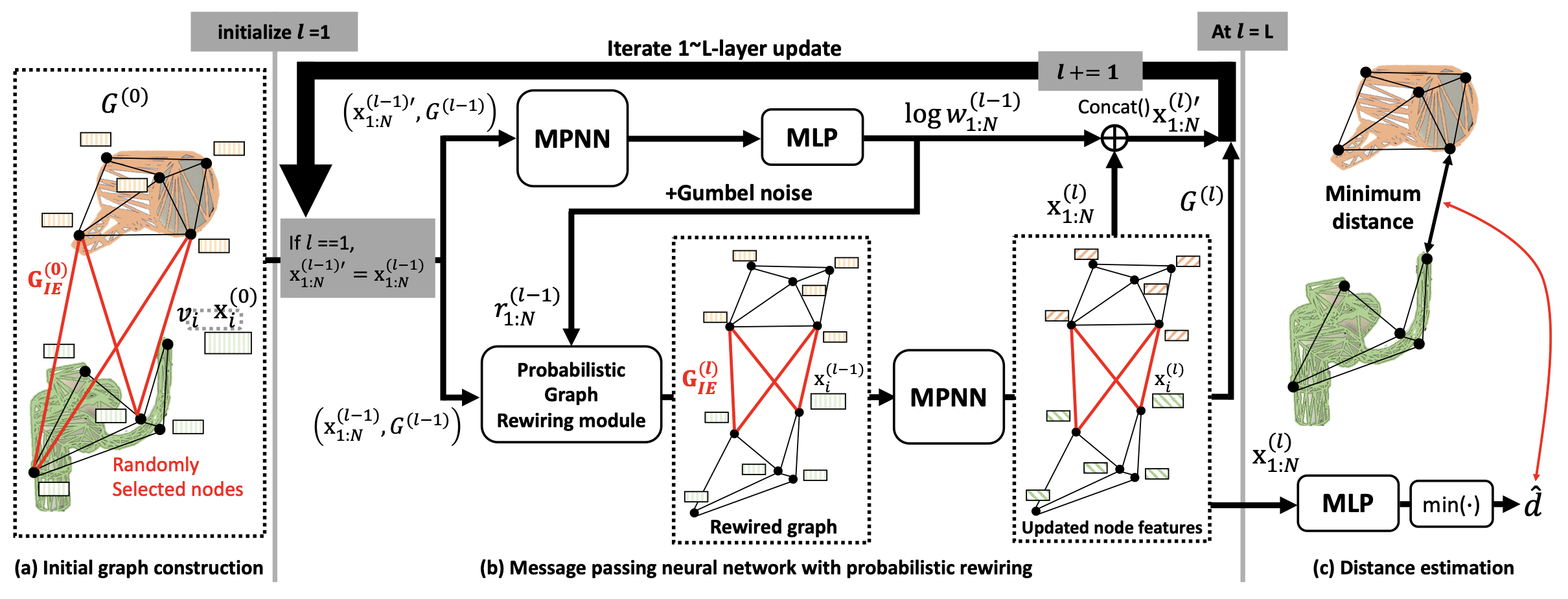
위 식에서 볼 수 있듯이 현재 노드와 연결된 모든 이웃 노드의 특징, 간선의 특징을 입력으로 받아 MLP를 통과시켜 메시지를 구하고, 그 모든 메시지를 더한 값을 다음 레이어의 노드 특징 벡터로 정합니다(기존 GNN에서는 메시지와 노드 특징 벡터를 다시 MLP에 통과시키는데, 이 논문에서는 그 부분이 빠짐). 여기에서 사용되는 MLP는 2개의 은닉층을 가지는 (16, 16) NN입니다. 따라서 MPNN의 레이어를 통과하는 순간부터 노드의 특징 벡터 길이는 16차원으로 바뀝니다.

Rewiring

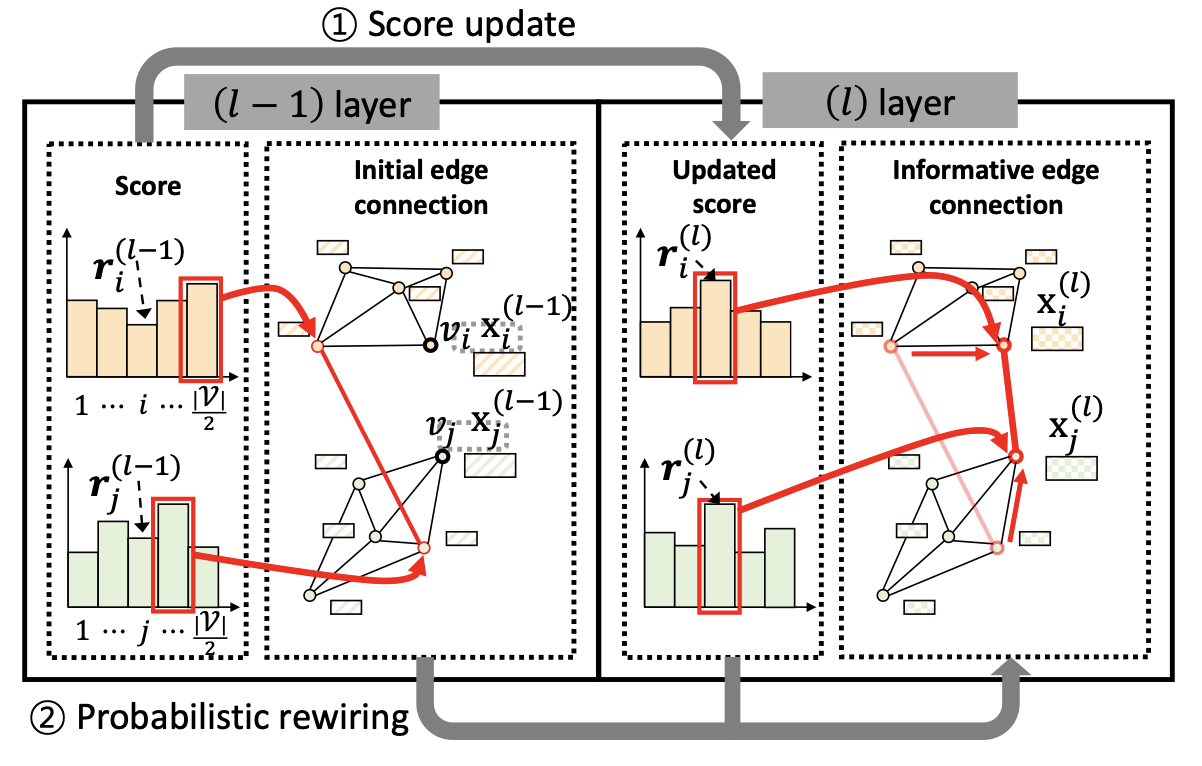
Rewiring은 각 레이어를 통과할 때마다 두 물체의 그래프를 연결하는 그래프인, $G_{IE}$를 수정하는 작업을 의미합니다. 이 작업을 수행하기 위해 각 노드가 얼마나 중요한지를 측정할 수 있어야 합니다. 이를 위해 단층 MPNN을 사용하는데, 첫 번째 레이어에서 Rewiring을 하는 방법과, 그 이후 두 번째 레이어에서부터 Rewiring을 하는 방법이 조금 다릅니다.

Initialization

\[[x_1^{(l)'}, ...,x_{|\mathcal V|}^{(l)'}]=\text{MPNN}(G^{(1)}, h_\theta) \quad \text{where } \quad h_\theta \text{ is (4, 4) MLP}\] \[\log w_i^{(l)} = M^T_Rx_i^{(l)'}\]

가장 처음 레이어에 대해서는 초기화된 그래프를 또 다른 단층 MPNN 네트워크(MLP로 (4, 4)를 사용하는)를 통과시켜 4차원짜리 노드 벡터를 얻습니다. 그리고 이 노드 벡터를 학습이 가능한 4차원 projection matrix와 곱해 하나의 스칼라 값으로 사영시킵니다. 그리고 이 값이 노드의 중요함을 나타내는 척도로 사용됩니다.

Update

\[[x_i^{(l)'}, \log w_i^{(l-1)}] \in \mathbb R^{17}\]

두 번째 레이어부터는 이전 레이어에서 얻은 $\log w_i^{(l-1)}$ 값을 적극 활용해, 이 값을 노드 특징 벡터와 함께 concat해 단층 MPNN을 통과시킵니다. 이 후로는 동일하게 4차원 projection matrix를 통해 스칼라 값으로 사영시키고 이 값을 이용해 그래프를 결정합니다.

\[r_i^{(l)} = \log w_i^{(l)} - \log(-\log u_i)\] \[u_i \sim Gumbel(0, 1)\]

단층 MPNN을 통해 얻은 중요도를 바로 사용하는 것이 아니라, 그 값에 Gumbel 노이즈를 추가시킵니다. 이렇게 노이즈를 추가시켜줌으로써 모델이 좀 더 다양한 노드의 연결에 대해 학습할 수 있게 됩니다. 노이즈가 추가된 스코어를 기반으로 Interconnection node를 선정하는데, 스코어가 높은 노드를 결정론적으로 선택할 경우 미분이 불가능하다는 단점이 존재합니다. 따라서 미분이 가능할 수 있도록 top-k relaxation method를 사용합니다. 이 방법론에서는 $\tau$를 통해 랜덤성을 결정할 수 있는데요, 실제 실험에서는 점차적으로 낮추거나 특정 값으로 고정해놓고 사용합니다.

Training and test of distance estimation

위의 과정을 통해 최종적으로 16차원짜리 노드 특징 벡터들이 남게 됩니다. 이 노드를 16차원짜리 projection matrix를 사용해 스칼라 값으로 사영시킵니다. 그리고 이 값이 거리를 나타내게 됩니다. 따라서 각 노드별로 거리가 나오게 되고, 그 중에서 가장 작은 값이 최소거리이므로, 아래와 같이 최종 추정 값을 말할 수 있습니다.

\[\min[d_1, ..., d_{|\mathcal V|}] = \min M^T_{out}[x_1^{(L)}, ..., x_{|\mathcal V|}^{(L)}]\]

이 값을 사용해 단순히 MSE Loss를 사용할 수도 있고, rewiring 과정 중에 수집한 중요도 점수를 사용할 수도 있습니다.

\[L_{\text{WIRE}} = \sum_{l=1}^{L}\sum_{i=1}^{|\mathcal V|}|d_{true} - d_i|\cdot r_i^{(l)}\]

MSE는 거리 오차를 줄여주는 역할을 하고, WIRE는 최적의 연걸을 했는지를 평가하기 때문에, 실제 실험에서는 두 손실함수를 번갈아 교체하면서 학습합니다.

Experiment Setup

모델을 평가하기 위해 OmniHang 벤치마크를 사용합니다. 총 5개의 카테고리(모자, 헤드폰, 가방, 가위, 머그컵)에 대해 10개씩, 총 50개의 물체가 사용되고, 이 물체를 걸어야 하는 U자형 고리가 총 3개로 총 150쌍의 상황이 존재합니다.

데이터 수집을 할 때, 처음에 mesh로 주어진 데이터에 대해 quadratic-error-metric을 사용해 다운샘플링된 그래프의 형태로 단순화 시킵니다. 물체-고리 configuration을 샘플링할 때 아래의 두 가지 전략을 사용합니다.

• Random Pose Sampling: 0.1cm의 간격으로 10cm 범위 내의 Cartesian Sapce 안에서 한 위치당 4개씩, 총 300,000개의 랜덤 포즈 데이터를 생성합니다.
• Sequential Sampling along Randomized Trajectories: RRT알고리즘을 사용해 10개의 이동 궤적을 만든 뒤, 해당 궤적에서 최소 거리가 0.02가 되는 포즈들을 샘플링합니다. 여기서 말하는 거리는 위치 거리와 쿼터니언 거리를 6대 4 비율로 합쳐서 사용합니다.

위와 같이 수집한 데이터를 1부터 10까지 임의의 배율로 스케일링해 다양한 스케일의 객체를 고려할 수 있게 했고, 거리가 0.2cm 미만이거나 5cm를 넘는 범위의 샘플들은 제거합니다. 총 41,412개의 샘플들이 최종적으로 남게되고, 아래의 두 가지 벤치마크 데이터셋으로 분류해 사용합니다.

• Seen categories: 알려진 물체 카테고리에 대해서 잘 동작하는지 확인합니다. 물체의 카테고리에 신경쓰지 않고 7:3 비율로 훈련 데이터와 테스트 데이터 집합을 나눠 사용합니다. 26,590개의 샘플들이 이 벤치마크 데이터셋에 속합니다.
• Unseen categories: 알려지지 않은 물체 카테고리에 대해서도 잘 임무를 수행하는지 확인합니다. 모자, 헤드폰, 가방만을 훈련할 때 사용하고, 테스트할 때에는 남은 카테고리에 대해서 수행합니다. 14,822개의 샘플들이 이 벤치마크 데이터셋에 속합니다.

다음으로 이 방법론이 TO(Trajectory Optimization)을 잘할 수 있는지 확인하기 위해 추가 실험을 수행합니다. 최적화를 수행하기 위해 제약 비용함수와 목적 비용함수가 사용됩니다.

\[constraint\_cost = w_c\sum_t \min(d_{safety} - \hat d_t, 0)\]

비용함수는 위와 같이 정의되는데, GDN-R이 예측한 거리가 안전거리로 설정해둔 거리보다 가까운지를 확인합니다. 그리고 남은 목적 비용함수는 생성된 궤적의 이어지는 포인트들의 거리의 모든 합으로 설정됩니다. 경로 위의 이어지는 포인트들의 거리를 목표 비용함수로 사용하면 불필요하게 돌아간다거나, 급하게 변하는 등의 경로로 설정하지 않게 할 수 있습니다.

Evaluation

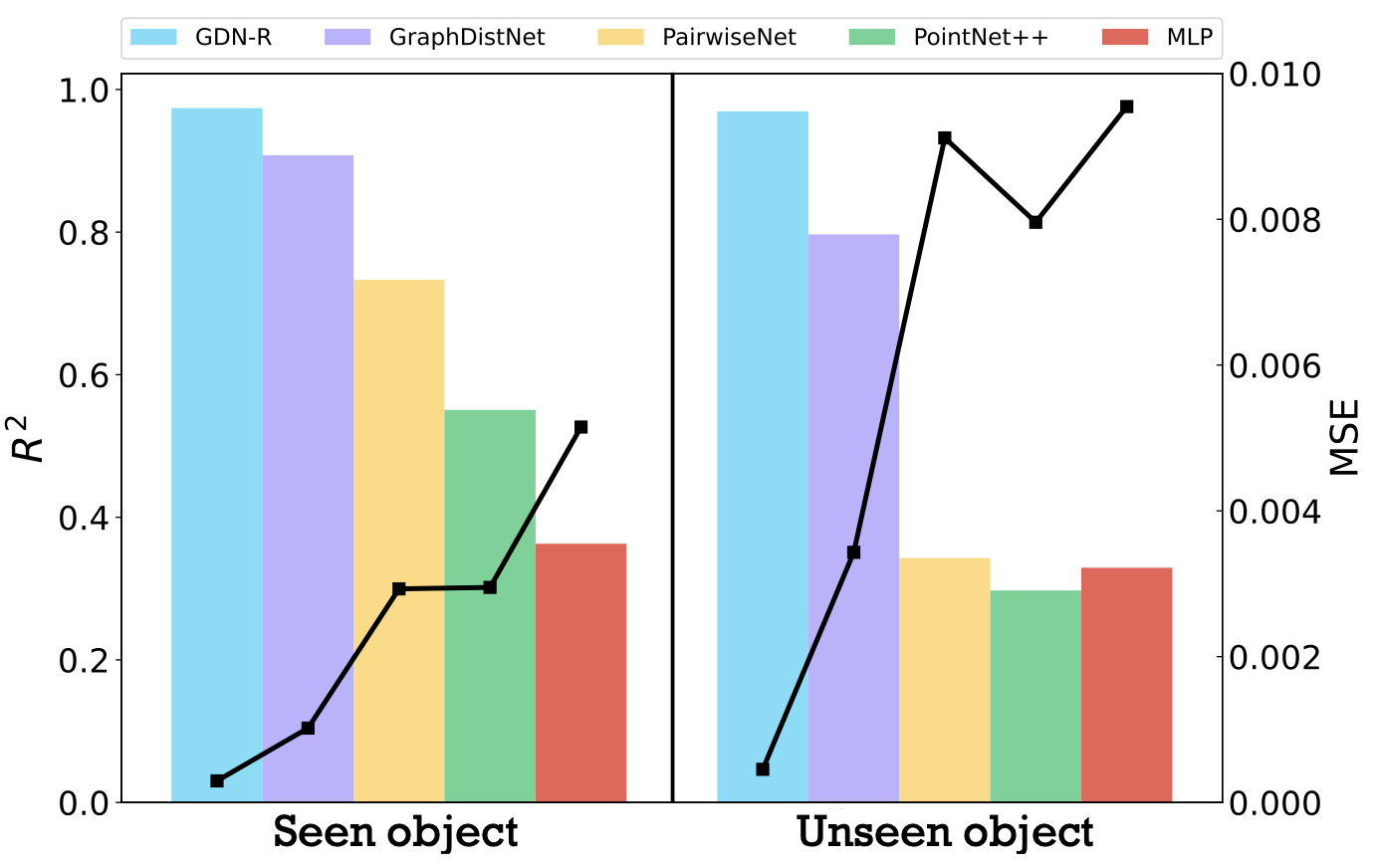
먼저 Seen category와 Unseen category의 비교에서, 이 논문에서 제안한 GDN-R의 성능이 모든 경우에서 가장 높은 성능을 보여줍니다. 이어서 이전에 소개한 GraphDistNet이 두 번째 높은 성능을 보여주는데, 이를 통해 GNN을 이용한 접근 방법이 최소 거리를 추정할 때 유리한 방법임을 확인할 수 있습니다.

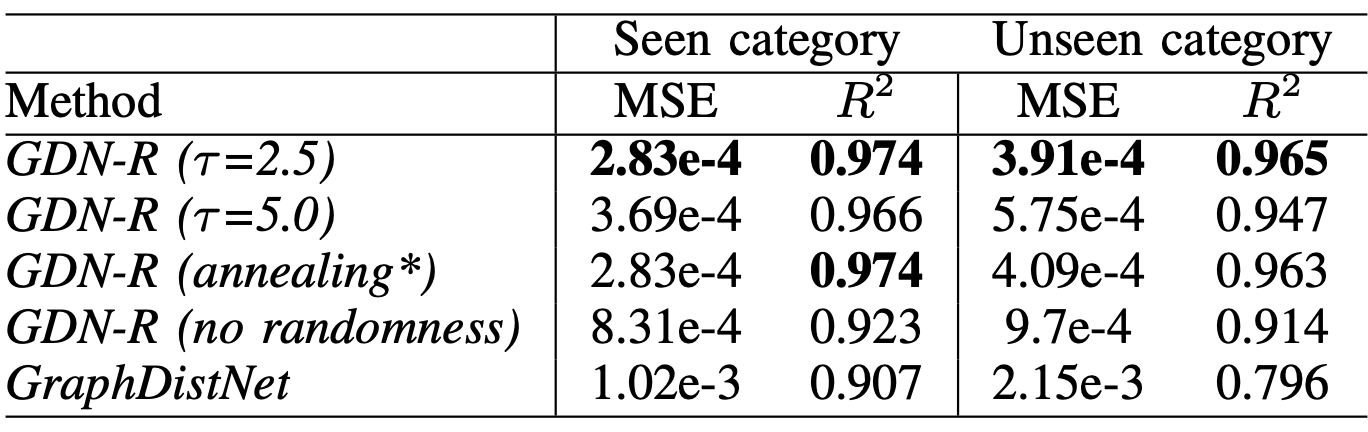
이어서 Rewiring 단계에서 추가되는 랜덤성을 주는 방법을 다양하게 비교해봤을 때, 2.5의 Temperature를 고정시켜 사용했을 때의 성능이 가장 좋게 나타납니다. Temperature를 통해 랜덤성을 부여했을 때, exploration 효과로 인해 더 좋은 성능을 보이는 것으로 생각됩니다. 다만, 너무 큰 Temperature를 설정했을 때 성능이 하락하는 것으로 보아, 적절한 조절이 필요해 보입니다.

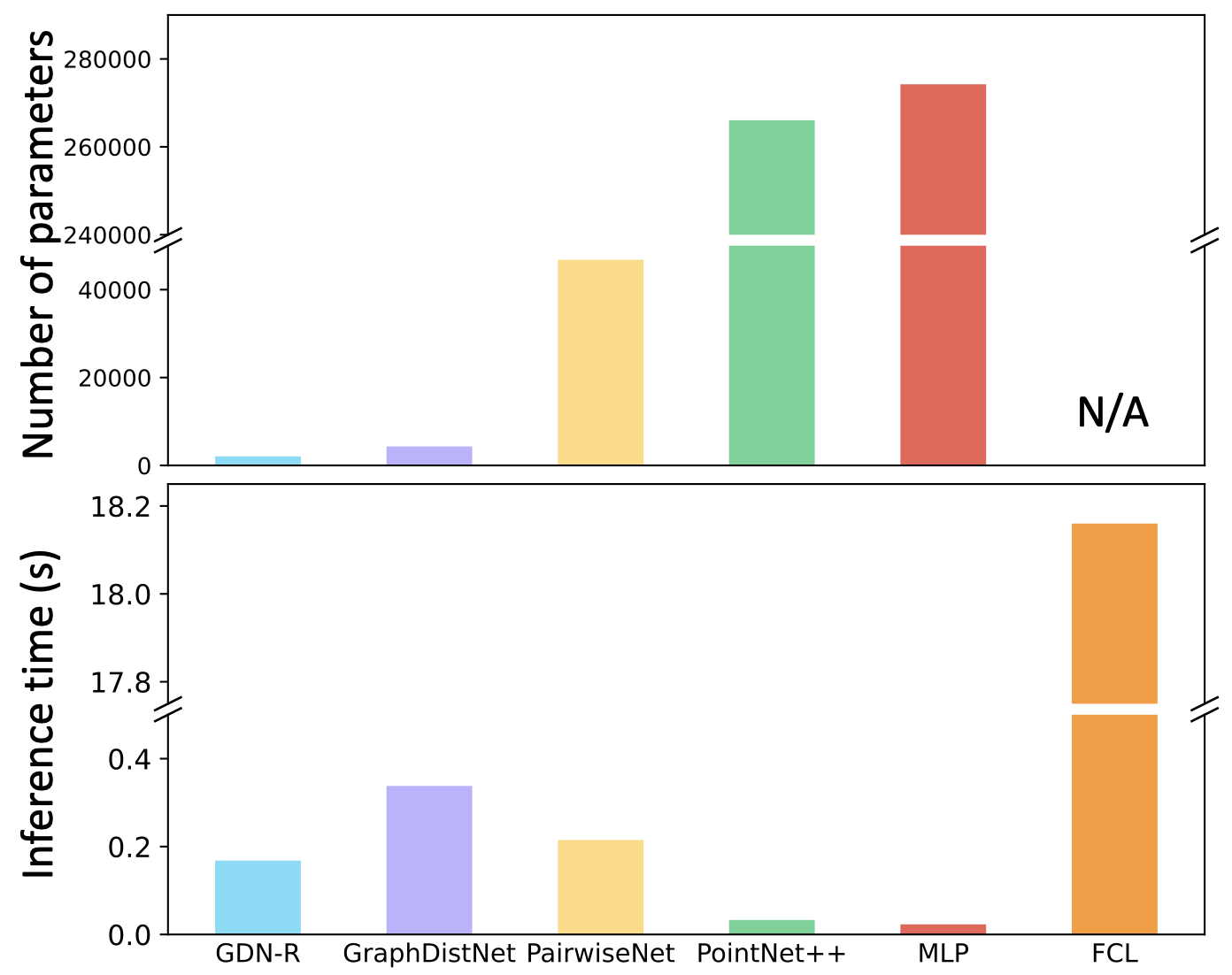
파라미터의 개수는 다른 방법론들과 비교했을 때 월등히 적게 사용하지만, 추론 시간에서는 이전에 제안한 GDN보다는 절반만큼 추론시간이 줄긴 했지만, PointNet++와 MLP랑 비교했을 때 훨씬 더 많은 시간을 사용합니다.

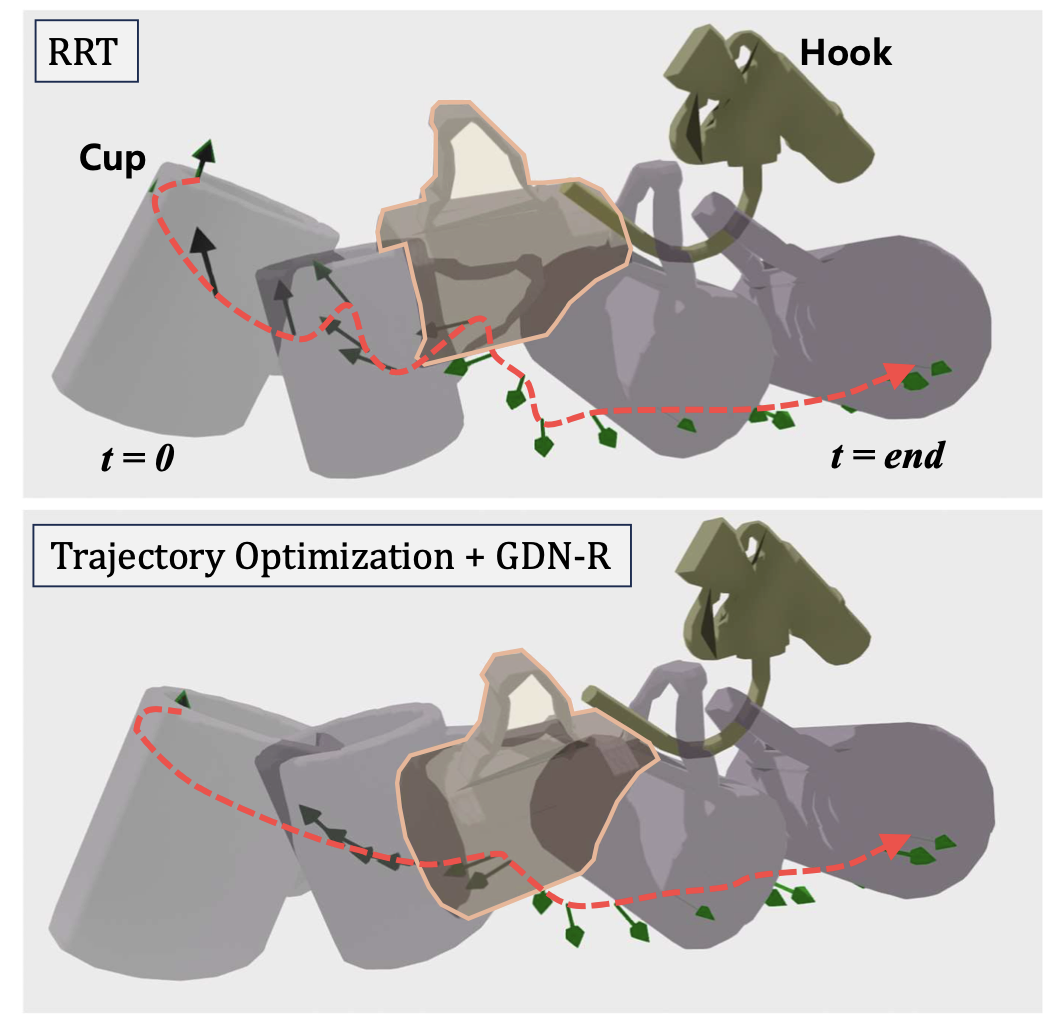
마지막으로 RRT로 생성한 궤적을 GDN-R을 사용했을 때, 최적화가 잘 되는지 평가하는데, 기존에 비뚤빼뚤했던 RRT 경로에서 매끄러우면서도 실행 가능한 경로를 얻을 수 있음을 보여줍니다.

Conclusion

미분 가능한 Gumbel Top-k 절차를 통해 이전에 제안했던 모델보다 사이즈를 줄이면서도 3차원의 물체까지 다룰 수 있도록 확장시킨 점이 인상깊은 점입니다. 추론시간이 조금 오래 걸리기는 하지만, 다른 기존 방법론들과 비교했을 때, 훨씬 더 좋은 성능을 보여줍니다.