Deterministic Policy Gradient Algorithms(DPG)

이 포스팅은 ‘Deterministic Policy Gradient Algorithms(DPG)‘에 대한 내용을 담고 있습니다.

논문 주소 및 자료 출처: https://proceedings.mlr.press/v32/silver14.pdf, http://proceedings.mlr.press/v32/silver14-supp.pdf, https://proceedings.neurips.cc/paper_files/paper/1999/file/464d828b85b0bed98e80ade0a5c43b0f-Paper.pdf, https://arxiv.org/pdf/1205.4839

Deterministic Policy Gradient Algorithms(DPG)

Deterministic Policy Gradient(DPG, 결정론적 정책 경사 알고리즘)는 강화학습 이론에서 다루는 정말 중요한 알고리즘 중 하나입니다. 결정론적 정책 경사 알고리즘 이전에는 확률론적 정채 경사 알고리즘들(예: REINFORCE)만이 존재했는데, 알고리즘의 구조상 연속적인 행동 공간을 가지는 환경에서 사용하기가 거의 불가능합니다.

\[\begin{bmatrix} a_1\\ a_2\\ a_3\\ \vdots \\ a_\infty \end{bmatrix} = \begin{bmatrix} \pi(a_1|s_t)\\ \pi(a_2|s_t)\\ \pi(a_3|s_t)\\ \vdots \\ \pi(a_\infty|s_t) \end{bmatrix}\]

확률론적 정책 경사 알고리즘에서는 각 행동별로 선택이 될 확률이 계산됩니다. 연속적인 행동 공간에서는 무한히 많은 행동이 존재하고, 이 모든 행동들에 대해 정책 확률을 부여하는 일은 매우 어렵습니다. 사실 연속적인 공간이 아니라, 다양한 액추에이터를 가지는 경우에서조차 알고리즘이 잘 동작하지 못합니다. 예를 들어 6축 로봇팔을 제어한다고 할 때, 각 모터의 범위를 0도부터 90도, 그리고 1도씩 discrete하게 행동공간을 정의해도 가능한 행동의 가짓 수가 무려 531,441,000,000개나 존재합니다. 때문에 이렇게 넓은 행동 공간을 가지는 경우에는 각 행동마다 선택할 확률을 부여하는 것이 아니라, 상태가 주어졌을 때, 다음 행동을 결정론적으로 선택하는 정책이 훨씬 더 유용합니다.

\[\mu_\theta(s) = a\]

생각해보면, 위와 같이 결정론적으로 정책 함수를 디자인하는게 떠올리기 어려운, 아주 새로운 아이디어는 아닌 것처럼 느껴집니다. 그렇다면 도대체 왜 2014년이 되어서야 제안이 되었고, 강화학습의 연속적인 행동 환경 문제에 있어서 이렇게까지 중요한 논문으로 다뤄지는걸까요?

확률론적 정책 경사 알고리즘만이 있었을 당시에 사람들은 모델이 없는 결정론적 정책 경사 알고리즘은 존재하지 않는다고 생각했습니다. 그 이유는 확률론적 정책 경사 알고리즘에서 사용되는 정책 경사 정리(Policy Gradient Theorem)(Sutton. 1999)을 결정론적 정책을 사용하는 경우에는 사용할 수 없다는 점에 있습니다. 이 논문에서는 새로운 접근 방법을 통해 정책 경사 정리가 결정론적 정책 경사 알고리즘에서도 존재함을 보입니다.

Introduction

먼저 당시 사람들이 왜 모델이 없는 결정론적 정책 경사 알고리즘에서는 정책 경사 정리가 존재하지 않는다고 생각했는지 설명하겠습니다. 아래는 정책 경사 정리의 증명입니다(Sutton. 1999).

Policy Gradient Theorem

에이전트에게 가이드가 되는 목표함수를 설정하는 방법에는 크게 두 가지가 있습니다. 하나는 모든 상태에서 받을 보상들에 대한 평균으로 설정하는 것이고, 다른 하나는 특정 상태에서 받을 보상으로 설정하는 방법입니다. Sutton의 정책 경사 정리에서는 두 가지 경우에서 모두 동일한 형태의 목표 기울기가 나타남을 보입니다.

\[\rho(\pi) = \lim_{n\rightarrow\infty}\frac{1}{n}E[r_1 + r_2 + \cdots + r_n|\pi] = \sum_sd^\pi(s)\sum_a\pi(s, a)R_s^a\] \[Q^\pi(s, a) = \sum_{t=1}^\infty E[r_t - \rho(\pi) | s_0 = s, a_0 = a, \pi]\]

위는 모든 상태에서 받을 보상에 대한 평균의 공식과 이 경우 사용되는 상태-가치 함수 식입니다. 이어서 위의 목표함수에 대한 기울기를 유도합니다.

\[V^\pi(s) = \sum_a\pi(s, a)Q^\pi(s, a)\]

양 변을 파라미터로 미분합니다.

\[\frac{\partial V^\pi(s)}{\partial \theta} = \frac{\partial }{\partial \theta}\sum_a\pi(s, a)Q^\pi(s, a)\] \[= \sum_a[\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \pi(s, a)\frac{\partial }{\partial \theta}Q^\pi(s, a)] \text{ (product rule)}\] \[= \sum_a[\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \pi(s, a)\frac{\partial }{\partial \theta}[R_s^a + \sum_{s'}P_{ss'}^aV^\pi(s')- \rho(\pi)]] \text{ (expand Q function)}\] \[= \sum_a[\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \pi(s, a)[ - \frac{\partial }{\partial \theta}\rho(\pi) + \sum_{s'}P_{ss'}^a\frac{\partial }{\partial \theta}V^\pi(s')]]\] \[= \sum_a[\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \pi(s, a)[\sum_{s'}P_{ss'}^a\frac{\partial }{\partial \theta}V^\pi(s')]]- \sum_a\pi(s, a)\frac{\partial }{\partial \theta}\rho(\pi)\] \[= \sum_a[\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \pi(s, a)[\sum_{s'}P_{ss'}^a\frac{\partial }{\partial \theta}V^\pi(s')]]- \frac{\partial }{\partial \theta}\rho(\pi)\]

정리한 꼴을 다시 정리합니다.

\[\frac{\partial V^\pi(s)}{\partial \theta} = \sum_a[\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \pi(s, a)[\sum_{s'}P_{ss'}^a\frac{\partial }{\partial \theta}V^\pi(s')]]- \frac{\partial }{\partial \theta}\rho(\pi)\] \[\frac{\partial }{\partial \theta}\rho(\pi) = \sum_a[\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \pi(s, a)[\sum_{s'}P_{ss'}^a\frac{\partial }{\partial \theta}V^\pi(s')]]- \frac{\partial V^\pi(s)}{\partial \theta}\] \[\sum_sd^\pi(s)\frac{\partial }{\partial \theta}\rho(\pi) = \sum_sd^\pi(s)[\sum_a[\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \pi(s, a)[\sum_{s'}P_{ss'}^a\frac{\partial }{\partial \theta}V^\pi(s')]]- \frac{\partial V^\pi(s)}{\partial \theta}]\]

전개하면…

\[\sum_sd^\pi(s)\frac{\partial }{\partial \theta}\rho(\pi) = \sum_sd^\pi(s)\sum_a\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) + \sum_sd^\pi(s)\sum_a\pi(s, a)\sum_{s'}P_{ss'}^a\frac{\partial }{\partial \theta}V^\pi(s')\] \[- \sum_sd^\pi(s)\frac{\partial V^\pi(s)}{\partial \theta}\] \[\sum_sd^\pi(s)\frac{\partial }{\partial \theta}\rho(\pi) = \sum_sd^\pi(s)\sum_a\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a) +\sum_{s'}d^\pi(s')\frac{\partial }{\partial \theta}V^\pi(s')\] \[- \sum_sd^\pi(s)\frac{\partial V^\pi(s)}{\partial \theta}\]

동일한 항을 제거하면…

\[\frac{\partial\rho }{\partial \theta} = \sum_sd^\pi(s)\sum_a\frac{\partial \pi(s, a)}{\partial \theta}Q^\pi(s, a)\]

마지막 식이 정책 경사 정리의 최종적인 꼴이 됩니다. 원문의 부록에서 두 번째 목표함수 설정에서도 동일한 꼴로 구해짐을 유도하는 과정을 확인할 수 있습니다.

결정론적 정책에서의 Policy Gradient Theorem

원문에서 위와 같이 전개를 할 때, 파라미터화된 정책을 파라미터에 대해 미분할 수 있음을 가정합니다. 그런데, 결정론적 정책(Deterministic Policy)의 경우 정책에 대한 미분을 구하는게 불가능합니다. 정책 분포는 확률 밀도 함수이기 때문에, 일반적으로 결정론적 정책과 같이 discrete한 정책을 나타내기 어렵지만, 디렉 델타 함수를 사용한다면 표현이 불가능하지는 않습니다.

\[\pi(a|s) = \delta(a - \mu_\theta(s))\]

그런데 위와 같은 임펄스 함수는 애당초 미분이 불가능하기 때문에 Sutton의 정책 경사 정리를 사용할 수 없습니다. 다시 돌아가서 목표함수의 꼴을 다른 형태로 살펴보겠습니다.

\[J(\tau) = E_{\sim\pi}[r(\tau)]\] \[J(\tau) = \int \pi(\tau) \cdot r(\tau)d\tau\] \[\nabla_\theta J(\tau) = \int \nabla_\theta\pi(\tau) \cdot r(\tau)d\tau\]

위 식의 값을 구하기 위해서는 정책을 파라미터로 미분한 값을 구해야 합니다(확률론적 정책 경사 알고리즘에서는 로그 트릭을 사용해 꼴을 변경하지만, 결정론적 정책의 경우 로그 정책의 치역이 정의되지 않기 때문에 사용할 수 없습니다).

\[\nabla_\theta\pi(\tau) = \nabla_\theta(p(s_0^\tau) \times \prod_{t=1}^{T}p(S_{t+1}|S_t, \mu(S_t)))\] \[= \nabla_\theta p(s_0^\tau) \times \prod_{t=1}^{T}p(S_{t+1}|S_t, \mu(S_t)) + p(s_0^\tau) \times \prod_{t=1}^{T}\nabla_\theta p(S_{t+1}|S_t, \mu(S_t))\] \[\nabla_\theta p(S_{t+1}|S_t, \mu(S_t)) = \nabla_\mu p(S_{t+1}|S_t, \mu) \times \nabla_\theta \mu(S_t)\]

정리하면, 상태 전이 확률의 행동에 대한 미분값을 알고있어야 목표함수에 대한 기울기를 구할 수 있는데, 환경에 대한 모델이 있을 때에만 이 값을 구할 수 있습니다. 이러한 이유로 모델이 없는 경우의 결정론적 경사 하강 알고리즘(Model-Free Deterministic Policy Gradient)는 존재하지 않는다고 생각되었습니다.

Deterministic Policy Gradient Theorem

아래는 논문의 Supplementary Material에서 보인 결정론적 정책 경사 정리의 유도 과정입니다.

\[\nabla_\theta V^{\mu_\theta}(s) = \nabla_\theta Q^{\mu_\theta}(s, \mu_\theta(s))\] \[= \nabla_\theta(r(s, \mu_\theta(s)) + \int_S\gamma p(s'|s, \mu_\theta(s))V^{\mu_\theta}(s')ds')\] \[= \nabla_\theta \mu_\theta(s) \nabla_ar(s, a)|_{a=\mu_\theta(s)} + \nabla_\theta\int_S\gamma p(s'|s, \mu_\theta(s))V^{\mu_\theta}(s')ds' \text{ (chain rule)}\] \[= \nabla_\theta \mu_\theta(s) \nabla_ar(s, a)|_{a=\mu_\theta(s)} + \int_S\gamma( \nabla_\theta p(s'|s, \mu_\theta(s))V^{\mu_\theta}(s') + p(s'|s, \mu_\theta(s))\space \nabla_\theta V^{\mu_\theta}(s'))ds' \text{ (product rule)}\] \[= \nabla_\theta \mu_\theta(s) \nabla_ar(s, a)|_{a=\mu_\theta(s)} + \int_S\gamma ( \nabla_\theta \mu_\theta(s) \nabla_ap(s'|s, a)|_{a = \mu_\theta(s)} V^{\mu_\theta}(s') + p(s'|s, \mu_\theta(s))\nabla_\theta V^{\mu_\theta}(s') )ds' \text{ (chain rule)}\]

위의 식에서 동일한 인수를 가지고 있는 항끼리 묶으면…

\[= \nabla_\theta \mu_\theta(s)\nabla_a(r(s, a) + \int_S \gamma p(s'| s, a)V^{\mu_\theta}(s')ds')|_{a=\mu_\theta(s)} + \int_S \gamma p(s'|s, \mu_\theta(s))\nabla_\theta V^{\mu_\theta}(s')ds'\] \[= \nabla_\theta \mu_\theta(s)\nabla_aQ^{\mu_\theta}(s, a)|_{a=\mu_\theta(s)} + \int_S \gamma p(s'|s, \mu_\theta(s))\nabla_\theta V^{\mu_\theta}(s')ds' \text{ (simplify to Q)}\] \[= \nabla_\theta \mu_\theta(s)\nabla_aQ^{\mu_\theta}(s, a)|_{a=\mu_\theta(s)} + \int_S \gamma p(s \rightarrow s', 1, \mu_\theta)\nabla_\theta V^{\mu_\theta}(s')ds'\]

정리하면…

\[\nabla_\theta V^{\mu_\theta}(s)= \nabla_\theta \mu_\theta(s)\nabla_aQ^{\mu_\theta}(s, a)|_{a=\mu_\theta(s)} + \int_S \gamma p(s \rightarrow s', 1, \mu_\theta)\nabla_\theta V^{\mu_\theta}(s')ds'\]

위와 같이 상태 함수를 상태 함수를 사용해 표현되는 점화식을 얻을 수 있습니다. 점화식을 사용해 식을 무한히 전개해나면, 아래와 같이 간단한 꼴로 정리됩니다.

\[\nabla_\theta V^{\mu_\theta}(s)= \int_S\sum_{t=0}^\infty \gamma^tp(s\rightarrow s', t, \mu_\theta)\nabla_\theta\mu_\theta(s') \nabla_aQ^{\mu_\theta}(s', a)|_{a=\mu_\theta(s')}ds'\]

위 식을 목적함수에 대입합니다.

\[\nabla_\theta J(\mu_\theta) = \nabla_\theta\int_Sp_1(s)V^{\mu_\theta}(s)ds\] \[= \int_Sp_1(s)\nabla_\theta V^{\mu_\theta}(s)ds\] \[=\int_S\int_S\sum_{t=0}^\infty \gamma^tp_1(s)p(s\rightarrow s', t, \mu_\theta)\nabla_\theta\mu_\theta(s') \nabla_aQ^{\mu_\theta}(s', a)|_{a=\mu_\theta(s')}ds'ds\] \[= \int_S \rho^{\mu_\theta}(s) \nabla_\theta\mu_\theta(s)\nabla_aQ^{\mu_\theta}(s, a)|_{a=\mu_\theta(s)}ds\] \[= E_{s\sim\rho^\mu}[\nabla_\theta\mu_\theta(s)\nabla_aQ^\mu(s, a)|_{a=\mu_\theta(s)}]\]

위와 같이 결정론적 정책 경사 정리를 유도할 수 있습니다. 기존의 정책 경사 정리와 비교할 때 꽤나 다른 전개 방향으로 정리를 얻어내긴 했지만, 기존의 정책 경사 정리와도 긴밀한 연관성을 찾을 수 있습니다. 결정론적 정책 경사는 확률론적 정책 경사의 특별한 경우로 해석될 수 있습니다. 확률론적 정책에 임의로 분산과 관련된 파라미터를 추가하고, 이 파라미터를 0으로 보내는 극한을 사용할 때, 결정론적 정책에서의 목적함수 기울기와 확률론적 정책에서의 목적함수 기울기가 동일함을 증명할 수 있습니다. 보다 자세한 증명은 논문의 supplementary material에서 확인할 수 있습니다.

Deterministic Actor Critic Algorithm

이제 위에서 얻은 결정론적 정책 경사 정리를 사용해 결정론적 정책 경사 알고리즘을 제안합니다. 기본적으로 Actor-Critic 구조를 사용하고, On-Policy인 경우를 먼저 살펴본 다음, Off-Policy인 경우를 살펴봅니다.

On-Policy Deterministic Actor Critic

정책이 결정론적인 경우에 On-Policy 방식을 사용하면 탐험을 적절하게 수행하지 못할 가능성이 높습니다. 환경에 노이즈가 많은 경우라면 잘 수행할 수도 있지만, 대부분의 경우에는 성공적이지 못할 가능성이 높습니다. 어찌됐건 On-Policy가 가장 직관적이면서도 기본적인 형태이기 때문에 이 경우에 어떻게 알고리즘이 나타나는지 살펴봅니다.

\[\delta_t = r_t + Q^w(s_{t+1}, a_{t+1}) - Q^w(s_t, a_t)\] \[w_{t+1} = w_t + \alpha_w\delta_t\nabla_wQ^w(s_t, a_t)\] \[\theta_{t+1} = \theta_t + \alpha_\theta \nabla_\theta\mu_\theta(s_t) \nabla_aQ^w(s_t, a_t)|_{a=\mu_\theta(s)}\]

순서대로 TD-Error, Critic Update, Actor Update를 수행합니다. Actor Update는 결정론적 경사 하강 정리에 따라서 수행됨을 확인할 수 있습니다. Critic Update의 경우 손실함수 값을 낮추기 위한 방향으로 이동합니다. 위는 MSE Loss를 사용한 경우의 업데이트 식입니다.

\[L(w) = \frac{1}{2}\delta_t^2\] \[\nabla_wL(w) = \delta_t\nabla_w\delta_t = \delta_t\nabla_wQ^w(s_t, a_t)\]

Off-Policy Deterministic Actor Critic

먼저 Off-Policy 확률론적 정책 경사(Off-PAC) 알고리즘을 먼저 알아보고, 이어서 Off-Policy 결정론적 정책 경사(OPDAC) 알고리즘을 살펴봅니다.

Off-PAC

\[J_\beta(\mu_\theta) = \int_S\rho^\beta(s)V^\pi(s)ds\] \[= \int_S\int_A\rho^\beta(s)\pi_\theta(a|s)Q^\pi(s, a)dads\]

어떤 경우가 되었든, 위와 같이 상태-행동 가치 함수의 꼴로 바꿔주어야 합니다. 왜냐하면 알고리즘 상에서 파라미터화된 상태-행동 가치 함수를 사용하기 때문입니다. 확률론적 정책 경사 알고리즘의 경우 위와 같이 행동에 대한 적분이 필연적으로 따라오게 됩니다.

\[\nabla_\theta J_\beta(\pi_\beta) = \int_S \int_A (\rho^\beta(s) \nabla_\theta\pi_\theta(a|s)Q^\pi(s, a) + \rho^\beta(s) \pi_\theta(a|s)\nabla_\theta Q^\pi(s, a))da ds\] \[\nabla_\theta J_\beta(\pi_\beta) \approx \int_S \int_A \rho^\beta(s) \nabla_\theta\pi_\theta(a|s)Q^\pi(s, a)da ds\]

위에서 Off-Policy 목적함수 경사가 근사값으로 표현되어 있는 것을 확인할 수 있습니다. 파라미터는 확률론적 정책 함수 뿐만 아니라 상태-행동 가치 함수에게도 영향력을 주는데요, 상태-행동 가치 함수에 대한 파라미터의 변화량을 측정하는 것이 너무 어려운 일이기 때문에, 엄밀하게는 곱미분의 형태로 두 개의 항이 존재해야하지만 계산의 편의를 위해 위의 근삿값을 목적함수의 기울기로 사용합니다(Degris et al.2012).

\[\nabla_\theta J_\beta(\pi_\beta) \approx E_{\sim \beta}[\frac{\pi_\theta(a|s)}{\beta_\theta(a|s)}\nabla_\theta \log \pi_\theta(a|s) Q^\theta(s, a)]\]

샘플링으로 값을 추정할 수 있게 식의 꼴을 위와 같이 정리합니다. 식의 구성 요소 중 중요도 비율을 확인할 수 있는데, 이를 통해 다른 분포로 부터 추출한 샘플이 가지는 편향을 없앨 수 있습니다. 중요도 샘플링은 다른 분포로부터 얻은 샘플을 사용할 수 있게 해준다는 큰 장점을 가지지만, 중요도 비율로 인해 매우 큰 분산을 가진다는 분명한 단점이 존재합니다.

OPDAC

\[J_\beta(\mu_\theta) = \int_S\rho^\beta(s)V^\mu(s)ds\] \[= \int_S\rho^\beta(s)Q^\mu(s, \mu_\theta(s))ds\]

양 변을 파라미터에 대해 미분합니다.

\[\nabla_\theta J_\beta(\mu_\theta) \approx \int_S \rho^\beta(s) \nabla_\theta\mu_\theta(s)Q^\mu(s, a)ds + \text{omitted}\]

Off-PAC에서와 동일하게 상태-행동 가치함수에 대한 기울기는 편의를 위해 다루지 않습니다. 식에서 확인할 수 있는 것은 행동에 대한 적분이 포함되지 않는다는 점입니다. 결정론적 정책에서는 행동이 곧바로 결정되기 때문에 행동에 대한 적분이 필요하지 않습니다.

\[\nabla_\theta J_\beta(\mu_\theta) \approx \int_S \rho^\beta(s)\nabla_\theta\mu_\theta(a|s)Q^\mu(s, a)ds\]

만약 디렉-델타 함수로 표현한다면, 위와 같은 모습이 될 것입니다. 그러나 디렉-델타 함수 특성상 행동에 대한 적분이 바로 붕괴되기 때문에 우리가 행동에 대한 적분을 마주할 일이 없게 됩니다.

\[= E_{s \sim \rho^\beta}[\nabla_\theta\mu_\theta(s)\nabla_aQ^\mu(s, a)|_{a=\mu_\theta(s)}]\]

정적 상태 분포를 사용해 기댓값의 꼴로 표현하면 위와 같습니다. 위 식의 좋은 점은 다른 정책을 가져다가 사용할 때, 중요도 비율이 곱해지지 않는다는 사실입니다. 따라서 다른 정책을 사용하면서도 낮은 분산으로 학습을 이어갈 수 있습니다.

\[\delta_t = r_t + \gamma Q^w(s_{t+1}, \mu_\theta(s_{t+1})) - Q^w(s_t, a_t)\] \[w_{t+1} = w_t + \alpha_w \delta_w \nabla_w Q^w(s_t, a_t)\] \[\theta_{t+1} = \theta_t + \alpha_\theta\nabla_\theta\mu_\theta(s_t) \nabla_aQ^w(s_t, a_t)|_{a=\mu_\theta(s)}\]

위의 OPDAC 업데이트 수식으로 Actor를 학습하고, MSE를 사용할 때의 Critic 업데이트 알고리즘입니다.

Compatible Function Approximation

근사 함수를 사용하면 항상 알고리즘의 수렴성이 보장되지 않는다는 문제가 있습니다. DPG 역시 기본적인 가치 함수를 사용할 때, 수렴성이 보장되지만, 비선형성이 포함된 가치 근사 함수를 사용할 때에는 수렴성을 보장하지 않습니다. 단, 아주 기초적인 근사 함수에서는 수렴성이 보장되는데, 그 조건은 아래와 같습니다.

\[\nabla_aQ^w(s, a)|_{a=\mu_\theta(s)} = \nabla_\theta\mu_\theta(s)^T w\] \[MSE(\theta, w) = E[\epsilon(s; \theta, w)^T\epsilon(s;\theta, w)]\] \[\text{where } \space \epsilon(s; \theta, w) = \nabla_aQ^w(s, a)|_{a=\mu_\theta(s)} - \nabla_aQ^\mu(s, a)|_{a=\mu_\theta(s)}\]

정리하면, 상태-행동 가치 함수가 오직 선형 근사의 꼴이면서, 손실함수로 MSE Loss를 사용할 때에만 수렴성이 보장됩니다. 위의 조건을 만족하는 근사 함수를 사용하는 알고리즘을 COPDAC(Compatible OPDAC)이라고 명명합니다.수렴성이 보장된다는 특성은 정말 좋지만, 최근에 사용되는 근사 함수의 꼴을 떠올려보면, 이런 꼴을 가지는 근사 함수가 사용될 것 같지는 않는 것 같습니다.

• 수렴성 보장 증명은 본 논문의 4.3장에서 확인할 수 있습니다.

Experiment

논문에서는 DPG를 사용한 총 세 가지 실험을 제시합니다.

• Continuous Bandit
• Continuous Reinforcement Learning
• Octopus Arm

Continuous Bandit

Continuous Bandit은 연속적인 행동 공간에서 레버를 당길 수 있도록 행동 공간이 정의된 문제입니다. 그러니까 레버를 당길 때 그냥 끝까지 당기거나 말거나, 두 가지 선택지가 아니라, 그 사이 어딘가로 당겼을 때 가장 보상이 높을 수 있도록 설정될 수 있습니다. 다양한 조건으로 실험이 수행되었는데, 행동의 차원이 10, 25, 50일 때 성능이 어떻게 변화되는지 측정합니다(밴딩 머신의 개수로 비유될 수 있음; 단, 밴딩 머신을 선택해서 당기는게 아니라 모든 밴딩 머신을 각각 당기는데 각 밴딩 머신을 독립적으로 원하는 만큼 당김). 모든 차원의 행동은 4일 때 가장 최적이도록 설정됩니다.

\[-r(a) = (a-a^*)^TC(a-a^*)\] \[a^* = \begin{bmatrix}4 & 4 & 4 & \cdots & 4\end{bmatrix}\]

비교 대상은 SAC-B(Stochastic Actor-Critic in the Bandit Task) 알고리즘입니다. SAC-B의 경우에는 이산적인 행동 공간에 확률을 부여하는 것이 아니라, 가우시안 행동 정책을 가지도록 설계되었습니다.

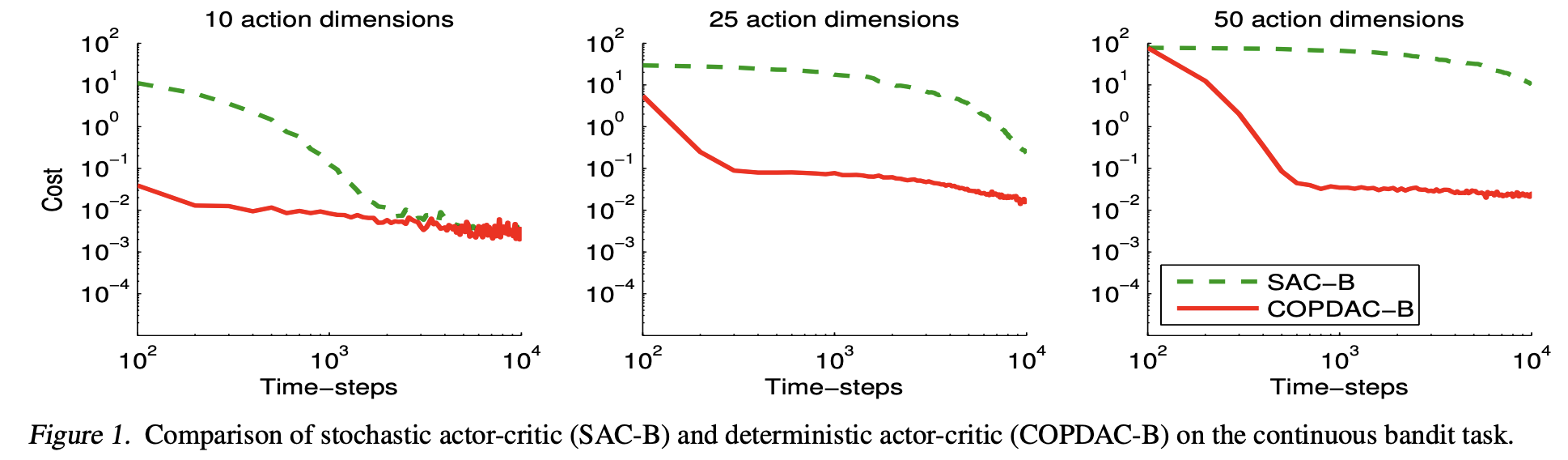
위의 실험 결과에서는 COPDAC-B에서 항상 더 좋은 성능을 보이는 것으로 나타납니다. 특히 행동 차원이 커질 때, SAC-B의 수렴 속도가 크게 감소하는 반면, COPDAC-B에서는 상대적으로 훨씬 준수한 수렴 속도를 유지하는 것을 확인할 수 있습니다.

Continuous Reinforcement Learning

강화학습 실험에 자주 등장하는 세 가지 환경(Mountain Car, Pendulum, 2D Puddle World)에서 각 알고리즘의 성능을 측정합니다. 이 실험에서는 SAC에 더해 OffPAC 알고리즘의 성능을 함께 제시합니다.

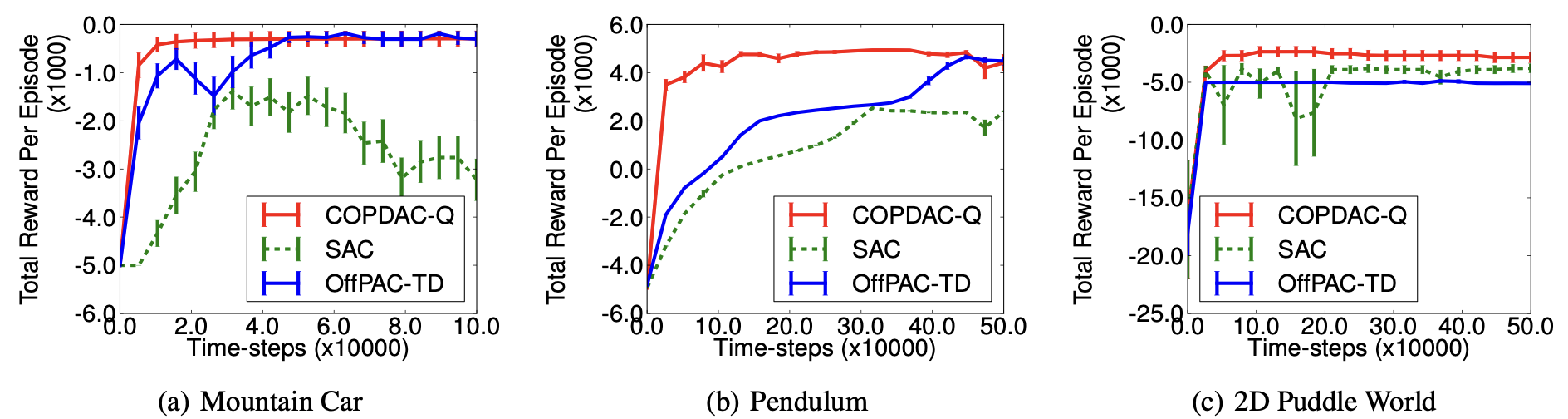
SAC의 경우 성능 붕괴가 일어나는 모습이 있는 한편, OffPAC과 COPDAC은 비교적 안정적인 성능을 보여줍니다. 그렇지만 COPDAC에서 특히 더 좋은 성능을 확인할 수 있고, 수렴 속도도 OffPAC과 비교할 때 훨씬 더 빠른 것으로 나타납니다.

Octopus Arm

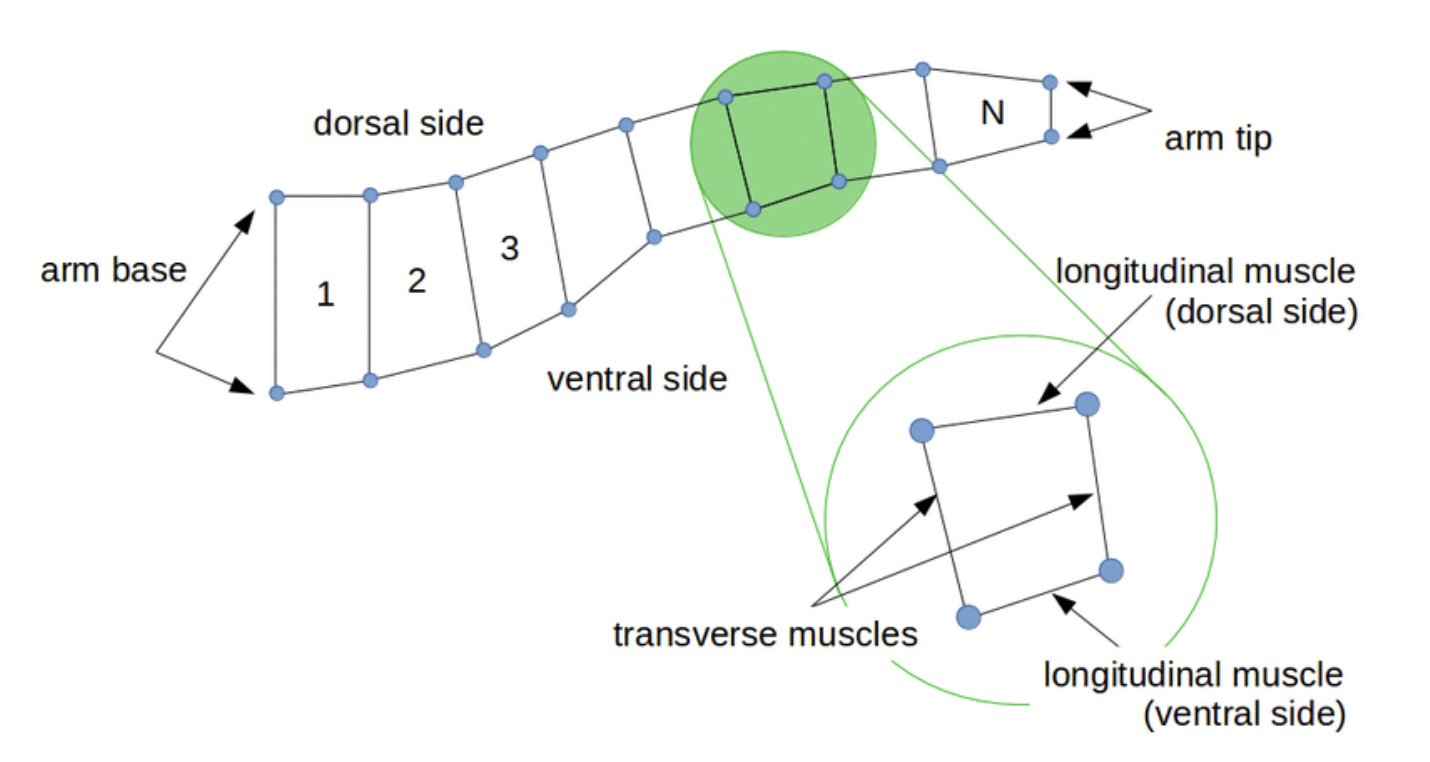
Octopus Arm은 목표를 쳤을 때 보상을 받도록 디자인된 시뮬레이션 태스크입니다. 한 번에 목표로 도달하는게 아니라, 여러 행동 시퀀스를 통해 목표에 도달하기 때문에, ‘몇 번의 행동을 거쳐 목표에 닿았는가’가 에피소드 당 받은 보상과 함께 알고리즘의 평가 척도로 사용됩니다.

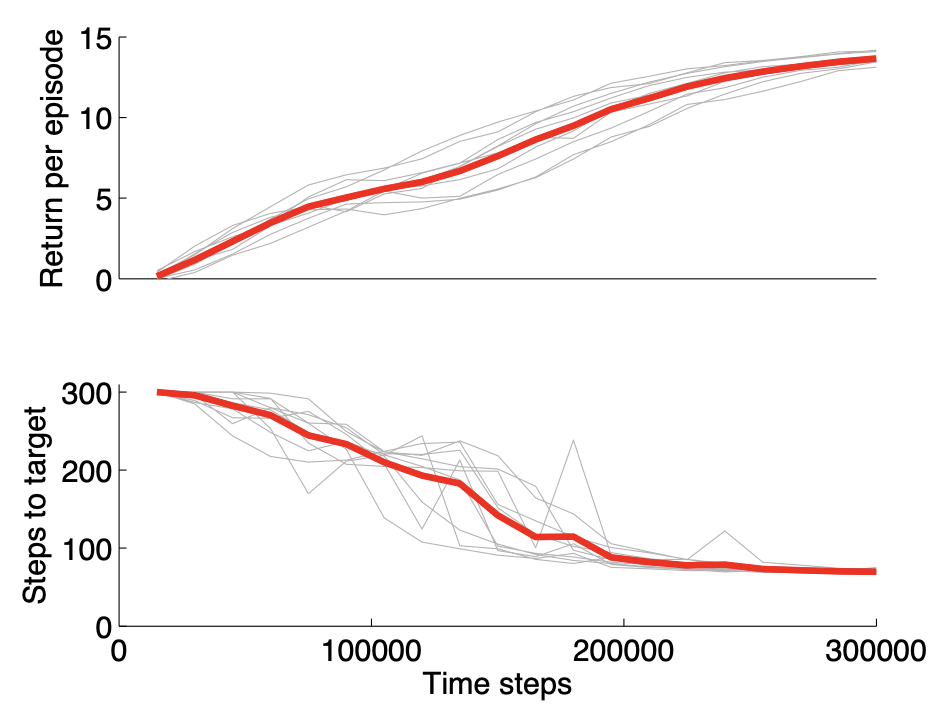
COPDAC 알고리즘을 사용했을 때 위와 같이 복잡한 연속 행동 공간 문제에서 안정적으로 수렴할 수 있음을 확인할 수 있습니다.

Conclusion

본 논문에서는 결정론적 정책 경사 알고리즘의 프레임워크를 제시합니다. 확률론적 방식과 달리 행동 공간에 적분을 필요로하지 않아 Off-Policy 환경에서 효율적으로 학습할 수 있습니다. 그리고 다양한 실험 환경에서 기존 알고리즘들에 비해 훨씬 더 높은 성능을 보여주고, Octopus Arm과 같이 매우 복잡한 강화학습 문제도 해결할 수 있음을 확인할 수 있습니다.