CDM: Contact Diffusion Model for Multi-Contact Point Localization

이 포스팅은 ‘CDM: Contact Diffusion Model for Multi-Contact Point Localization‘에 대한 내용을 담고 있습니다.

논문 주소: https://arxiv.org/pdf/2502.06109

CDM: Contact Diffusion Model for Multi-Contact Point Localization

최근 많이 사용되는 협동로봇들은 사람들과 동일한 작업 공간에서 일을 수행하기 때문에, 항상 충돌의 위험을 가지고 있습니다. 때문에 로봇이 환경과의 예상치 못한 충돌을 일으킨다면 그 충돌을 감지할 수 있어야 하고, 로봇의 어느 부분에 충돌이 발생했는지도 빠르게 감지할 수 있어야 합니다. 이런 필요로 인해 로봇의 충돌 위치를 감지하는 Contact Localization에 대한 몇 가지 연구들이 있었고, 단일 충돌 상황에 대해 어느정도 정확한 충돌 지점 예측이 가능하긴 했지만, 여러 지점에서 동시에 충돌(Multi-Contact Localization)하는 경우의 예측 성능은 많이 낮았습니다. 이 논문에서는 Diffusion Model을 사용하는 CDM이라는 새로운 모델로 높은 Mult-Contact Localization 성능을 보여줍니다.

Introduction

로봇의 충돌을 감지하는 방법론으로는 크게 두 가지가 있습니다. 하나는 학습 기반 방법론이고, 다른 하나는 모델 기반 접근 방법론입니다. 학습 기반 방법론에서는 문제를 접촉/ 비접촉 카테고리로 분류합니다. 이전 연구들에서는 모델의 접촉 부위를 자세하게 찾아낸다기 보단 다소 간소화해서(base를 0, end-effector를 1로 설정) 접촉 부위를 예측합니다. 모델 기반 접근 방법론에서는 대개 Particle Filter를 사용합니다. Particle을 랜덤으로 흩뿌린 다음, 로봇의 관절 토크 센서가 말하는 값을 가장 잘 설명하는 위치로 점점 수렴하는 방향으로 충돌 지점을 탐색합니다.

예측 값과 실제 값 사이의 오차는 QP(Quadratic Programming)으로 정의되는데요, 충돌 지점 감지 문제에는 항상 특이점(Singularity)가 존재합니다. 여기서 말하는 특이점이란, 동일한 토크를 발생시키는 충돌 위치가 2개 이상 존재함을 의미합니다. 즉, QP error가 낮은 지점이 여러개 존재할 수 있는데, Particle Filter를 사용하는 경우에 가능한 여러 해답들 중 하나로 수렴하게 됩니다. 이런 문제를 해결하기 위해 여러 초기 지점을 설정해 다양한 해답 지점을 찾으려는 시도가 있었지만, 이 접근법은 단일 충돌 지점 감지 문제에서만 제한적으로 사용됩니다.

다중 충돌 감지 문제에서는 특이점 문제가 더 많이 발생합니다. Particle Filter를 사용할 때 다중 충돌 감지 문제를 다루기 위해 과거의 관측 정보를 사용하는 방법이 있습니다. 만약 이중 충돌이 연속적으로 발생한다면, 단일 충돌 감지를 연속으로 두 번 해결하는 문제로 환원시킬 수 있습니다. 실제 연구 사례에서는 초기 Particle Set으로 예측을 하다가 일정 임계치 이상으로 오류가 발생하면 추가적인 새로운 Particle Set을 초기화하는 방법론이 있었습니다. 하지만 적절한 임계치가 얼마인지 조절하는 것은 꽤나 어려운 일입니다.

이 논문에서는 충돌 Singularity 문제를 없애는 것이 아니라 특이점 발생 가능성을 남겨두는 한편, 충돌 지점을 보다 정확하게 예측하기 위한 새로운 방법론을 소개합니다. 특이점이 있다는 것은 확률론적 관점으로는 충돌 지점 분포가 Multi-Modal(볼록한 모양이 여러 개)이라는 건데요, 이 Multi-Modal 분포를 잘 예측하는 것이 이 논문의 목표가 됩니다.

Preliminaries

CDM 모델을 이해하기 위한 사전 지식을 먼저 소개합니다.

Contact Induced Sensor Measurements

\[\mathcal{W}_{ext} = \begin{bmatrix}\tau_{ext} \\ \mathcal{F}_{ext}\end{bmatrix} = \sum_{i=1}^{n_c} \underbrace{ \begin{bmatrix} J_i^T(q, r_i) \\ I_{3 \times 3} \\ skew(r_i) \\ \end{bmatrix}}_{A_i(q, r_i)} F_i\]

위 식은 로봇이 받는 힘과 각 관절 힘, 토크 및 베이스에 걸리는 힘, 토크 사이의 관계입니다. 위 식에서의 $\mathcal{W}_{ext}$는 모멘텀 기반의 DOB(Disturbance Observer, 외란 관측기)나 EDOB(Extended DOB)를 통해 그 예측값을 얻을 수 있습니다.

여기서 $\tau_{ext}$는 각 관절에 걸리는 토크를, $\mathcal{F_{ext}}$ 는 로봇의 베이스에 걸리는 힘과 토크를 의미합니다. 로봇에 부착된 센서를 통해 토크를 측정할 수 있는데요, 이 값을 바로 사용하는 것이 아니라 DOB를 사용해 Disturbance(외란)이 제거된 값($\hat{\mathcal{W}}_{ext}$)을 추정합니다.

Optimization-based Contact Point Localization

\[\mathrm{QP}(\hat{\mathcal{W}}_{ext} \mid r) = \min_{F} \left\lVert \hat{\mathcal{W}}_{ext} - \sum_{i=1}^{n_c} A_i(q, r_i) F_i \right\rVert^2 \quad \text{subject to} \quad F_i \in \mathcal{F}_c(r_i), \,\forall i \in \{1, \dots, n_c\}\]

위는 2차 계획법의 목적함수와 제약식입니다. 위 식에서 우리는 오차를 최소화 하는 $F_i$를 찾아야 합니다. 이때 구해지는 힘 벡터는 Friction Cone 내부에 존재해야 합니다.

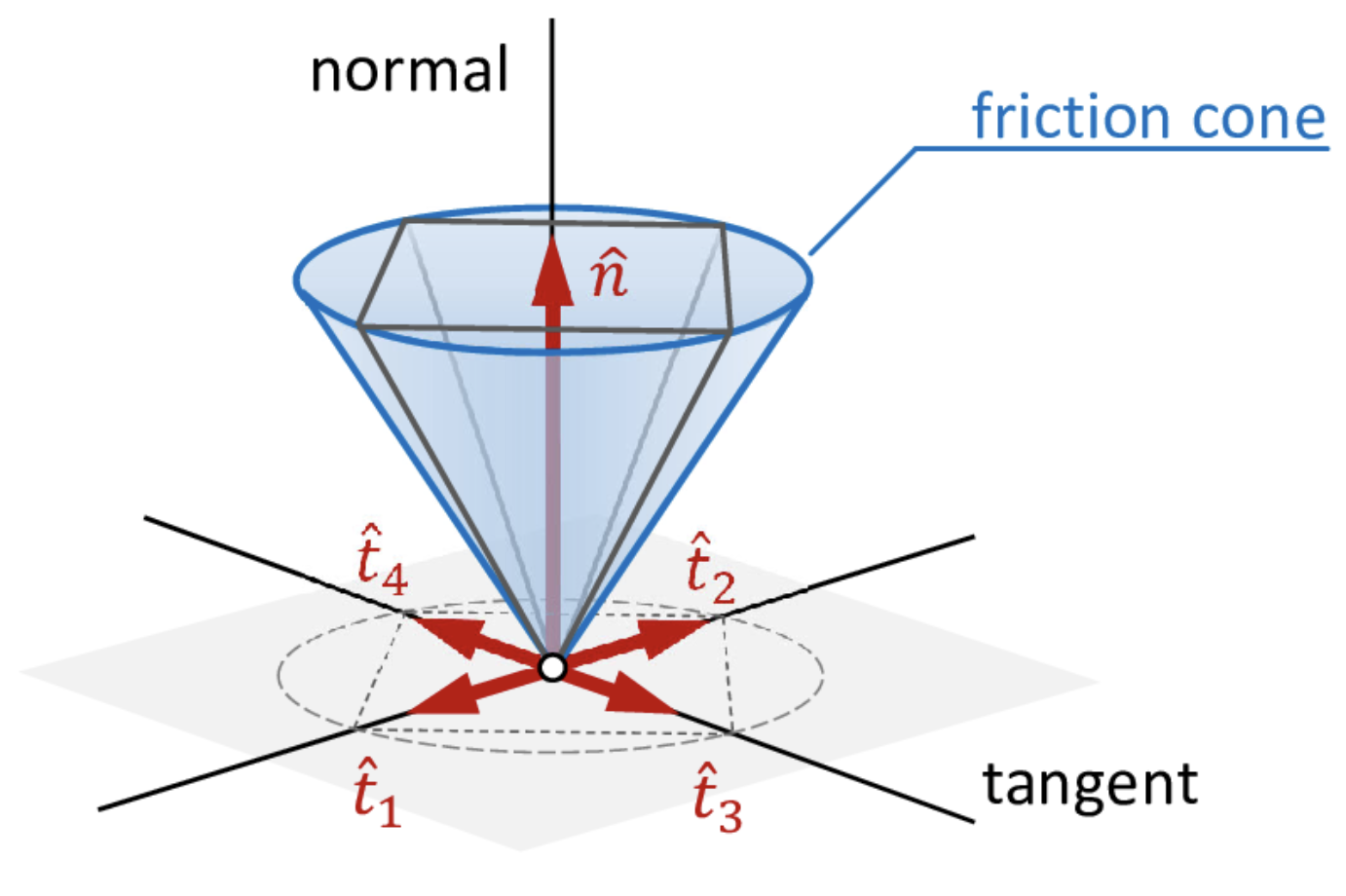
• Contact and friction simulation for computer graphics - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/A-friction-cone-approximated-by-normal-directionidirection-directioni-i-and-four_fig6_353790043 [accessed 18 Feb 2025]

Friction Cone이란 물체에 고정된 상태에서 힘을 가할 수 있는 공간을 의미합니다.

DDPM(Denosing Diffusion Probabilistic Models)

확산(Diffusion) 모델은 랜덤한 노이즈로부터 조금씩 여러 번 변형시켜 관심있는 대상의 분포가 되도록 바꾸는 확률적 생성 모델입니다. 확산 모델은 먼저 관심있는 대상 분포에 노이즈를 점차적으로 추가시켜 완전히 노이즈로만 가득차도록 바꿉니다. 그리고 이 변형을 역방향으로 학습해 완전한 노이즈로부터 관심있는 대상 분포로의 변형을 이끌어냅니다.

\[q\bigl(x[k] \mid x[k-1]\bigr) = \mathcal{N}\Bigl( x[k];\, \sqrt{1 - \beta_k} \, x^{[k-1]},\, \beta_k I \Bigr)\] \[q\bigl(x[k] \mid x[0]\bigr) = \mathcal{N}\Bigl( x[k];\, \sqrt{\overline{\alpha}_k}\, x^{[0]},\, \bigl(1 - \overline{\alpha}_k\bigr)\, I \Bigr)\] \[\text{where} \quad \alpha_k = 1 - \beta_k, \quad \overline{\alpha}_k = \prod_{i=1}^k \alpha_i\]

위는 관심 분포 대상에 노이즈를 추가해나가는 정방향 과정을 나타내는 수식입니다. 원본 데이터에 노이즈가 씌워나가는 과정은 반드시 Iterative하게 수행할 필요가 없습니다. 노이즈 스케줄링 정보를 알고 있다면, 한 번에 특정 스텝의 노이즈가 낀 이미지를 만들어 낼 수 있는데, 그게 위의 두 번째 수식의 갖는 의미입니다.

\[p_\theta\bigl(x^{[k-1]} \mid x^{[k]},\, k\bigr) = \mathcal{N}\Bigl( x^{[k-1]};\, \mu_\theta\bigl(x^{[k]}, k\bigr),\, \tilde{\beta}_k \, I \Bigr)\] \[\text{where} \quad \tilde\beta_k = \beta_k(1-\bar{\alpha}_{k-1})/(1-\bar{\alpha}_{k})\] \[\mu_\theta\bigl(x^{[k]},\,k\bigr) = \frac{1}{\sqrt{\alpha_k}} \bigl( x^{[k]} - \frac{1 - \alpha_k}{\sqrt{1 - \overline{\alpha}_k}} \, \epsilon_\theta\bigl(x^{[k]},\, k\bigr) \bigr).\]

인공 신경망을 학습시켜 노이즈 제거 네트워크인 $\epsilon_\theta\bigl(x^{[k]},\, k\bigr)$를 적절하게 추정하고, 완전한 노이즈로부터 관심 분포 대상으로 이동시키는 역방향 과정을 수행합니다. 역방향 과정에서 한 단계, 한 단계 이동 노이즈가 사라진 분포(마찬가지로 가우시안 분포)에서 계속 새로운 샘플을 추출합니다. ‘역방향 과정에서 노이즈가 사라져가는 분포로 이동을 하는데, 이 가우시안 분포의 평균과 분산이 어떻게 되는가?’가 확산 모델의 파라미터가 찾아야 하는 값이 됩니다. 그런데, 해당 가우시안 분포의 평균과 분산을 바로 예측하는 하는 것보다 단계별로 추가된 노이즈를 먼저 예측하는 것이 학습에 훨씬 유리합니다. 따라서 아래와 같이 손실함수를 정의합니다.

\[L_\theta = \mathbb{E}_{k,\, x^{[0]},\, \epsilon} \Bigl\lVert \epsilon - \epsilon_\theta\bigl(x^{[k]},\, k\bigr) \Bigr\rVert^2\]

CDM(Contact Diffusion Model)

CDM에서는 Diffusion Model을 사용해 처음에 랜덤으로 뿌려진 점들로부터, 가장 가능성이 높은 충돌 지점으로 천천히 수렴해 나갑니다. 아래에서 구체적으로 살펴봅니다.

Problem Statements

CDM에서 예측하고자 하는 대상은 힘이 가해진 위치입니다.

\[r_t = \{r_{t, i}\}_{i=1}^{n_c} \in \mathbb{R}^{n_c \times 3}\] \[p(r_t|O_{1:t}, \mathcal{S})\]

이 논문에서는 총 2개의 충돌 지점이 있는 경우까지를 다루기 때문에 $r_t$는 1 by 3 또는 2 by 3 행렬이 됩니다. 모델은 충돌 위치에 대한 분포를 처음부터 현재까지의 관측 데이터와 로봇 표면에 대한 정보를 기반으로 추정합니다.

그런데, 로봇이 수집하는 모든 데이터를 기반으로 예측을 수행하는 것은 메모리 상으로나, 추론 시간상으로나 어려움이 많습니다. 따라서 특정한 시간 길이($T$)만큼의 관측 데이터들만을 기반으로 충돌 위치를 추정합니다. 그리고 다중 충돌 감지의 경우 순차적으로 충돌이 발생할 수 있는데요, 이 경우에는 처음 충돌한 위치를 모델에게 넣어주어 다중 충돌 감지를 더 잘할 수 있도록 해줍니다. 이를 모두 적용한 수식을 아래에서 확인할 수 있습니다.

\[p\bigl(r_{t} \mid O_{t-T:t}, r_{T_s}, \mathcal{S}\bigr)\]

Dataset of CDM

\[\mathcal{D} = \{\xi_i\}_{i=1}^{N_d}\]

위와 같이 데이터를 에피소드의 집합으로 표현할 수 있는데, 에피소드는 충돌 지점, 그리고 연속 관측 데이터들로 구성됩니다. 구체적으로 적으면 아래와 같습니다.

\[\xi = \bigl\{ X_{t}^{[0]},\, O_{t-T:t} \bigr\}, \quad\text{where}\quad X_t \in \mathbb{R}^{n_p \times 3}.\]

[0] 표시는 노이즈가 적용되기 이전의 원본 위치임을 의미합니다. $X_t$의 크기는 해당되는 타임 스텝에서 접촉하고 있는 지점의 개수에 상관없이 동일하게 $n_p$ by 3 으로 고정합니다. 왜냐하면 $n_c$는 타임 스텝에 따라, 태스크의 종류에 따라 개수가 변하게 되는데, 이렇게 통일되지 않은 크기로 다루는 것이 어렵기 때문입니다.

\[O = \{ \hat{\mathcal{W}}_{ext}, q, \underbrace{T_l}_{(p_l, q_l)} \}\]

데이터의 관측 데이터는 위와 같이 구성됩니다. 센서 측정을 통해 구한 $\hat{\mathcal{W}}_{ext}$, 각 관절의 각도를 의미하는 $q$, 그리고 링크의 위치($p_l$)와 자세($q_l$)를 포함하는 $T_l$로 구성됩니다.

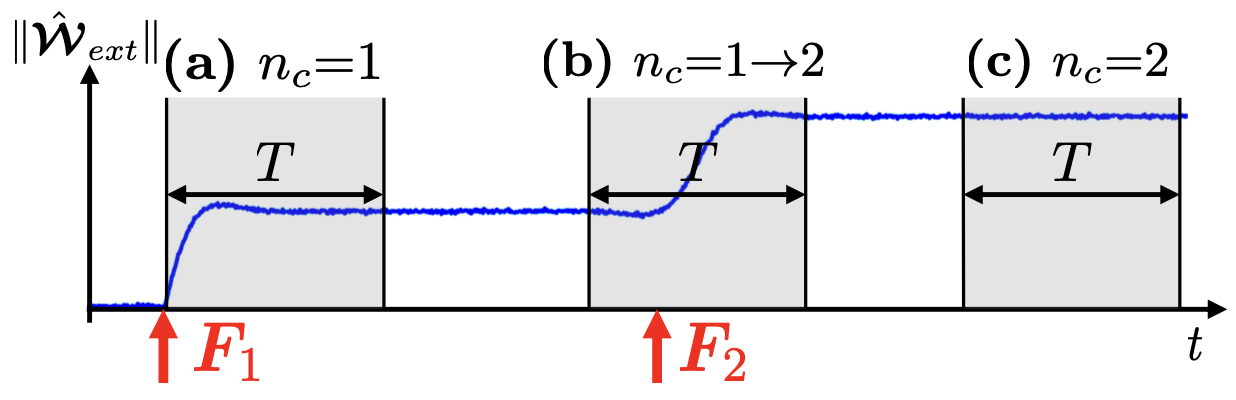
예를 들어, 위와 같이 총 2번의 접촉이 발생하는 경우 관측 데이터로 단일 접촉, 전이 이중 접촉, 이중 접촉이라는 세 가지 타입이 모두 수집됩니다.

Architecture

\[\hat{X}_t \sim p_{\theta}\bigl(X_t \mid O_{t-T:t},\, X_{T_s},\, S\bigr)\]

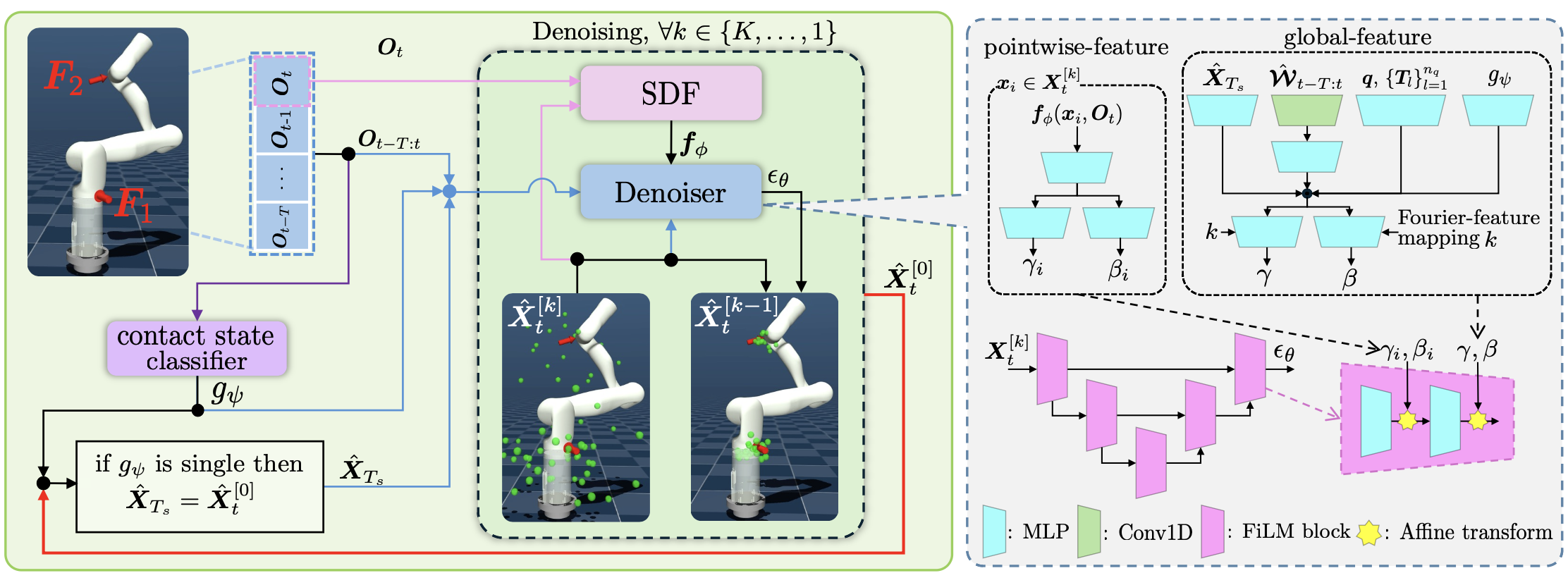
CDM의 목표는 위와 같이 파라미터로 추정되는 분포에서 샘플을 생성해 내는 것으로 정의됩니다.

Training

이제 실제로 위의 수식이 어떻게 적용되는지 구체적으로 살펴봅니다. 위 수식에서 골치아픈 부분은 사전 지식으로 들어가는 $X_T$, 이전 접촉 위치입니다. 이전에 접촉했던 위치를 모델에 제공하면 그 다음에 접촉한 두 번째 접촉 위치를 더 잘 추론할 수 있다는 아이디어인데, 문제는 태스크에 따라 이전 접촉 위치의 존재가 달라진다는 점에 있습니다.

예를 들어 단일 접촉 시나리오에서는 이전 접촉 위치가 존재하지 않지만, 이중 접촉 시나리오에서는 이전 접촉 위치가 존재합니다. 이중 접촉 시나리오에서는 이전 접촉 위치를 넣어주면 되는데, 단일 접촉 시나리오에서는 무엇을 넣어줘야 하는지 애매해집니다. 따라서 그 두 시나리오를 구분하지 않고 무조건 첫 번째 접촉 위치를 모델의 사전 지식으로 넣어줍니다. 그런데, 바로 넣어주는 것이 아니라 디퓨전 노이징이 가해진 첫 번째 접촉 위치를 넣어줍니다.

\[\hat X_{T_s} = r^{[k_h]}_{t, 1} \quad where \quad k_h \sim \mathcal{U}(1, K)\]

위와 같이 정보를 제공하면 노이즈가 없이 정보가 제공된 경우와 여러 번의 디퓨전 노이징 스텝으로 인해 랜덤 노이즈가 상당히 많이 가해진 경우, 모두에서 학습이 수행되기 때문에 여러 상황에서 모델이 일관되게 대응하도록 학습시킬 수 있습니다.

Inference

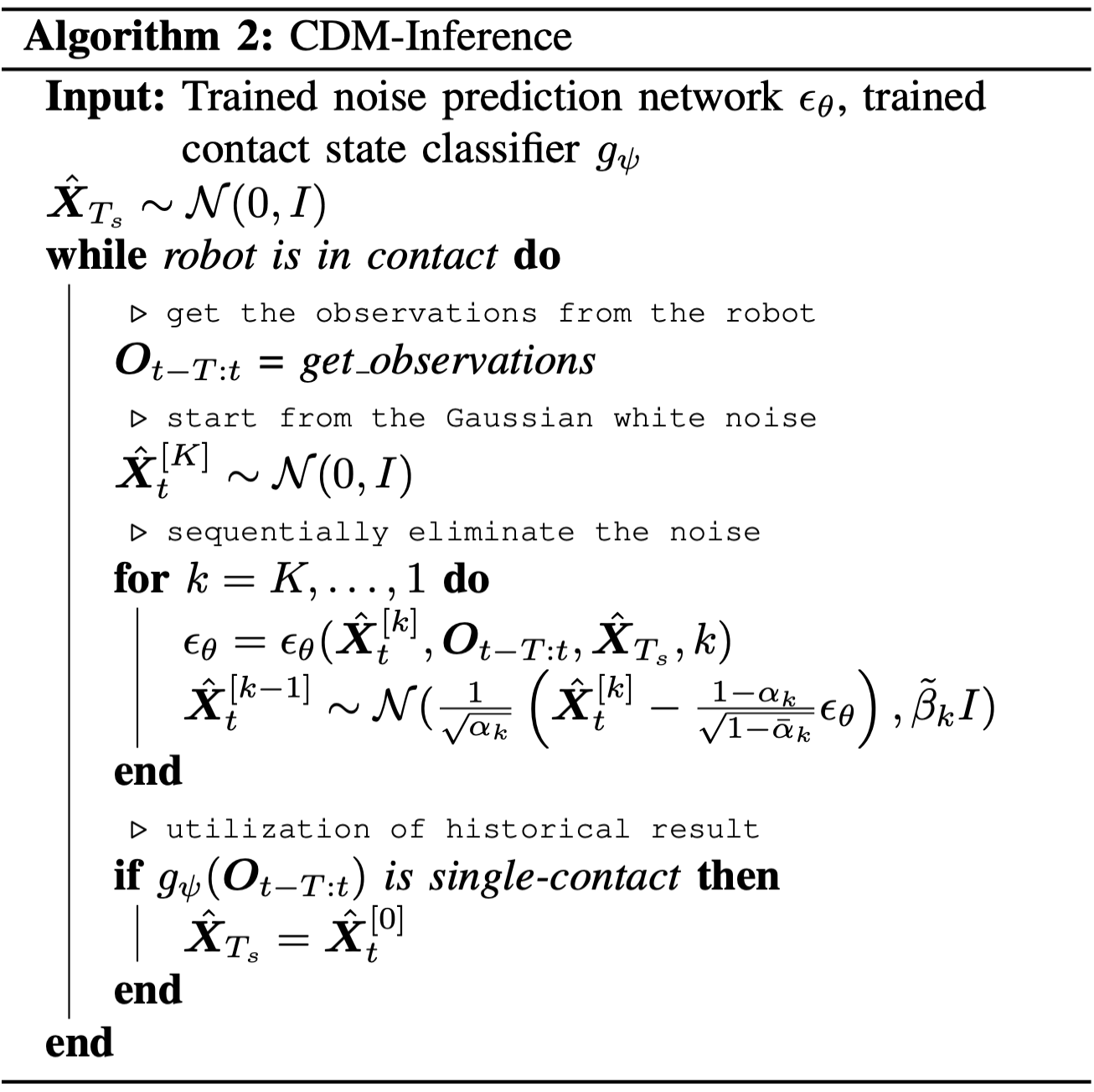
학습 단계에서는 첫 번째 접촉 위치가 주어지기 때문에 이전 접촉 위치를 넣어줄 수 있었는데, 추론 단계에서는 이전 접촉 위치를 알지 못하는 상태로 시작합니다. 따라서 해당 입력으로 랜덤 가우시안 노이즈를 넣어줍니다(학습 단계에서 노이즈가 많은 경우에 대해서도 학습하기 때문에 잘 동작할 수 있음). 그리고 확산 모델의 역방향 과정을 수행해 접촉 위치의 분포를 뽑아냅니다.

\[g_{\psi}(O_{t-T: t})\]

추론 단계에서 이중 접촉의 경우 이전에 추론한 위치를 사용해야 하는데요, 위의 신경망을 사용해 현재 관측 정보가 단일 접촉 상황이라고 판단되면, 이전 접촉 위치에 현재 추정된 접촉 위치를 업데이트합니다.

• 단일 접촉 시나리오: 단일 접촉 상태에서는 모델이 비교적 정확하게 위치를 추정합니다. 이 경우 추론된 접촉 위치의 신뢰성이 높기 때문에 추론 위치를 이전 접촉 위치로 업데이트 했을 때, 잘못된 정보가 들어갈 위험성이 낮습니다.
• 전이 이중 접촉 시나리오: 단일 접촉 상황에서 추정된 위치가 이전 접촉 위치로 업데이트된 상황에서 새로운 접촉이 발생하면, 이전에 추정한 첫 번째 위치를 바탕으로 두 번째 위치를 훨씬 더 수월하게 추정합니다.
• 이중 접촉 시나리오: 동시에 두 개의 접촉이 일어난 경우, 이전 접촉 위치를 어떤 위치로 정하는 것은 오히려 추정에 부정적인 영향을 미칠 수 있기 때문에, 어떤 값으로 갱신하지 않고 랜덤 노이즈를 그대로 사용합니다.

Surface Constraints Conditioning

접촉 위치 분포가 로봇의 링크 표면으로 잘 수렴하게 만들기 위해, 관련 정보를 모델에 추가로 넣어줍니다.

\[(d_l, g_l) = f_{\phi_l}(x_i, O_t) \in \mathbb{R^4}\]

점의 위치, 그리고 관측 정보를 입력으로 받아 특정 링크까지의 최단 거리와, 최단 지점으로의 벡터를 출력으로 하는 SDF 네트워크를 학습시킵니다. SDF 네트워크는 링크마다 선언되어, 링크 개수만큼의 순서쌍을 얻게 됩니다. 이 정보를 제약으로 넣어 분포가 로봇의 표면에 잘 수렴할 수 있도록 해줍니다.

Neural Network Model

Denoiser 모델은 여느 다른 확산 모델과 동일하게 U-Net 아키텍쳐를 사용하지만, 몇 가지 다른 점들이 존재합니다. 하나는 컨볼루션 층이 아닌 MLP 층을 사용한다는 점이고, 다른 하나는 로봇 표면으로의 수렴 제약과 더불어 전역적인 특징들을 만족하기 위한 제약을 FiLM 구조를 사용해 정보를 주입한다는 점입니다.

\[h_2 = W_1^Th_1\] \[h_3 = \gamma_ih_2 + \beta_i \quad \text{FiLM (SDF)}\] \[h_4 = W_2^Th_3\] \[h_5 = \gamma h_4 + \beta \quad \text{FiLM (Global Feature)}\]

FiLM은 일종의 Affine Transformation이라고 생각할 수 있습니다. 위에서 SDF 네트워크를 통해 얻은 거리 정보를 바탕으로 각 점마다 따로따로 FiLM을 수행하고, 다시 전역 특징들을 갖고 인공신경망의 결과로 얻은 값으로 모든 값에 대해 동일한 FiLM을 적용합니다. 두 번째 FiLM의 입력이 되는 전역 특징들은 Architecture 바로 아래의 도식에서 확인할 수 있습니다. (DOB로 얻은 $\hat{\mathcal{W}}_{ext}$을 사용하지 않고 현재의 관측치를 바로 사용합니다.)

Experiments

시뮬레이션 환경으로는 MuJoCo가 사용됩니다. 에피소드의 길이는 300ms로 0ms 지점에서 첫 번째 접촉이 발생하고, 절반인 150ms 지점에서 두 번째 접촉이 발생합니다. 그리고 현실 환경과 비슷하게 실험하기 위해 관절 토크 센서에 노이즈가 추가됩니다. 총 614,400개의 시뮬레이션 경로가 수집되었고, 90%는 학습에, 10%는 테스트에 사용됩니다.

CDM으로 생성된 샘플의 타당성 평가

각 상황 별로 얼마나 정확하게 위치를 추정했는지를 보여줍니다. 단일 접촉의 경우에 가장 낮은 오차를 보여주고, 전이 이중 접촉, 이중 접촉의 경우 전체적으로 오차가 증가하는 것을 확인할 수 있습니다.

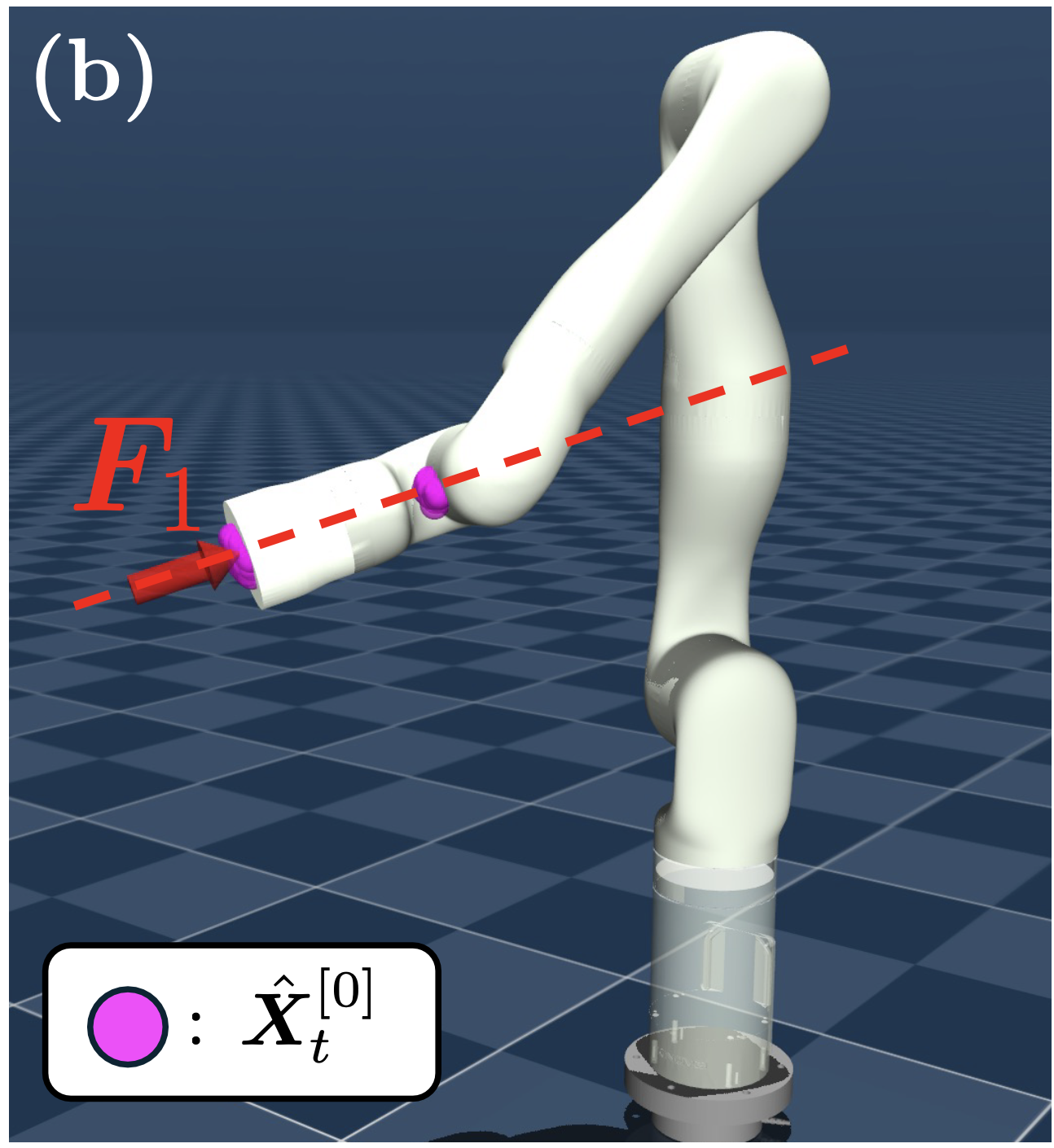
위의 그림은 단일 접촉 상황에서 접촉 위치가 두 개로 나타나는 경우입니다. 이처럼 단일 접촉 상황에서도 다중 모달성을 가질 수 있는 경우에 둘 모두를 동시에 생성할 수 있음을 확인할 수 있습니다.

SDF 제약에 대한 Ablation Study

표면 제약이 접촉 지점 추정에 미치는 영향에 대한 Ablation Study 결과는 아래와 같습니다.

• SDF를 포함했을 때의 로봇 표면과 추정 지점과의 평균 거리: 0.29cm
• SDF를 포함하지 않을 때의 로봇 표면과 추정 지점과의 평균 거리: 0.89cm

SDF 제약이 포함될 때 샘플들이 포봇 표면 근처로 잘 위치하게 강제할 수 있음을 확인할 수 있습니다.

Historical Diffusion Result Conditioning에 대한 Ablation Study

이전 접촉 지점에 대한 정보를 갱신해 다음 추론에 사용하는 것의 영향력을 측정합니다.

CDM-his는 하나의 에피소드의 다양한 부분을 넣어줘 이전 접촉 지점이 업데이트되게 만들고, CDM-null에서는 에피소드의 마지막 60ms만을 넣어줘 이전 접촉 지점을 사용하지 않습니다. Historical Diffusion Result Conditioning을 사용하지 않는 경우에는 기존의 PF 기반 알고리즘보다도 성능이 낮게 나타납니다.

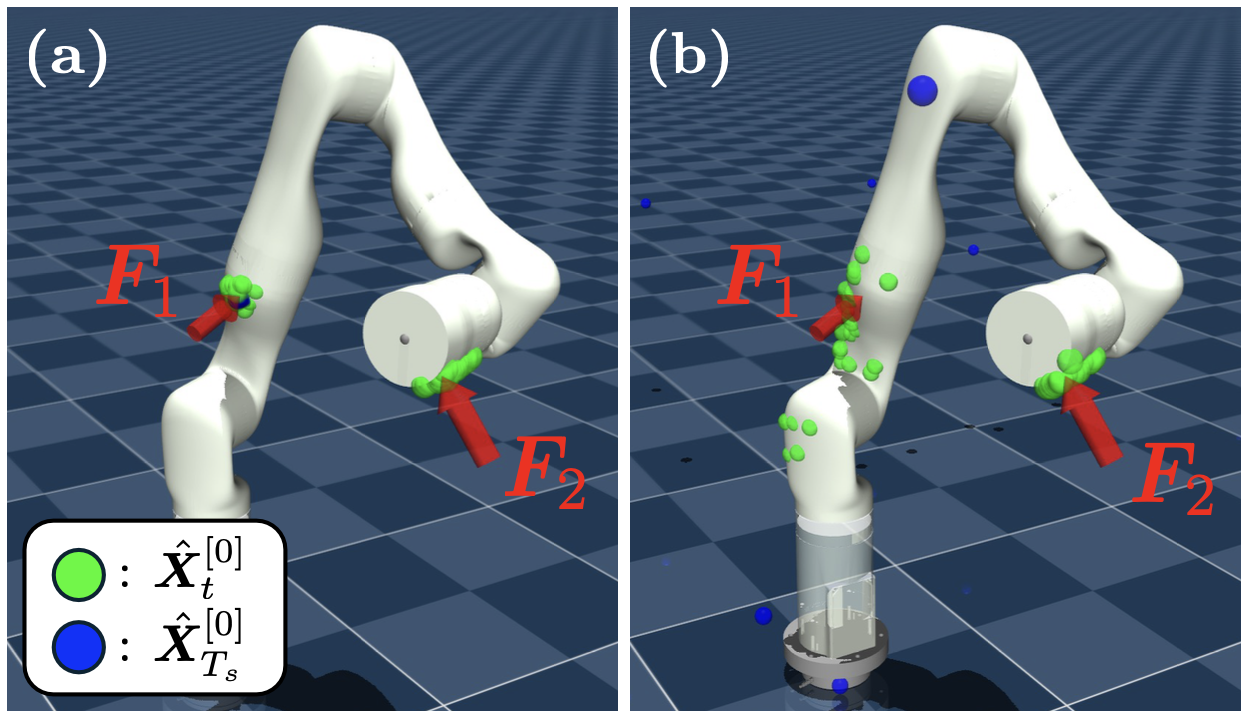
왼쪽은 Historical Diffusion Result Conditioning을 사용하는 경우이고, 오른쪽은 사용하지 않은 경우입니다. 사용한 경우과 비교했을 때 사용하지 않은 경우의 점의 분포가 상당히 퍼지게 나타나는 것을 확인할 수 있습니다.

Direct Sim-to-Real Transfer

시뮬레이션에서 학습한 모델의 실제 현실 환경에서의 성능을 측정합니다.

시뮬레이션에서의 성능과 비교했을 때 오차가 조금 더 늘기는 하지만, 현실 환경에서 수행된 이전 연구들과 비교했을 때 월등히 낮은 오차를 확인할 수 있습니다.

Conclusion

이 논문에서 소개된 CDM은 단일 접촉, 이중 접촉에서 모두 높은 성능을 보여줍니다. 생성 모델을 활용한 접촉 지점을 추정한 첫 번째 시도라는 점에 의의가 있습니다. 접촉 지점에 더해 접촉력을 함께 추정하는 것을 미래 연구 방향으로 제시합니다.