라플라스 변환(Laplace Transform)

이 포스팅은 ‘라플라스 변환‘에 대한 내용을 담고 있습니다.

자료 출처: https://www.youtube.com/playlist?list=PLbJ_QJGE4c4ioWGWpam2yVva7b3DzwlrE

라플라스 변환(Laplace Transform)

라플라스 변환은 공학에서 정말 많이 사용되는 도구 중 하나입니다. 라플라스 변환을 쓰는 가장 큰 이유는 미적분 방정식을 쉽게 풀 수 있다는 점에 있습니다. 그리고 주파수 응답을 시각적으로 쉽게 이해할 수 있도록 직관을 제공하는 장점도 있습니다.

\[\mathcal{L}[f(t)] = \int_0^\infty f(t)e^{-st} dt = F(s)\]

라플라스 변환은 위와 같이 정의됩니다. $t$에 대한 함수 뒤에 지수 함수를 곱한 다음, 0부터 무한대까지 적분하여 구합니다. 따라서 지수항의 계수인 $s$만 남게 되어 결과적으로는 $s$에 대한 함수가 됩니다. 다양한 함수들의 라플라스 변환을 어떻게 하는지, 이 라플라스 변환이 구체적으로 어떤 의미를 갖는지 이어서 살펴보겠습니다.

대표적인 라플라스 변환 공식

\[\mathcal{L}[C] = \frac{C}{s}\] \[\mathcal{L}[t^n] = \frac{n!}{s^{n+1}}\] \[\mathcal{L}[e^{at}] = \frac{1}{s-a}\] \[\mathcal{L}[\cos\omega t] = \frac{s}{s^2 + \omega^2}\] \[\mathcal{L}[\sin\omega t] = \frac{\omega}{s^2 + \omega^2}\]

위 4개 공식들은 대표적인 라플라스 변환 공식입니다. 가장 기본적인 형태의 라플라스 변환이기 때문에 많은 곳에서 자주 사용됩니다. 따라서 위의 변환 공식들은 반드시 알아두어야 합니다.

라플라스 변환의 선형성

라플라스 변환이 선형성을 가지는지 확인해보겠습니다.

\[\mathcal{L}[\alpha f(t) + \beta g(t)] = \alpha \mathcal{L}[f(t)] + \beta\mathcal{L}[g(t)]\]

선형성을 가진다는 것은 ‘위의 관계식이 성립하는가?’입니다. 라플라스 변환은 적분으로 정의되기 때문에 사실 선형성이 거의 보장되는데요, 실제로 그러한지 살펴보겠습니다.

\[\mathcal{L}[\alpha f(t) + \beta g(t)]\] \[\int_0^\infty (\alpha f(t) + \beta g(t))e^{-st} dt\] \[\int_0^\infty \alpha f(t)e^{-st} + \beta g(t)e^{-st} dt\] \[\int_0^\infty \alpha f(t)e^{-st}dt + \int_0^\infty\beta g(t)e^{-st} dt\] \[\int_0^\infty \alpha f(t)e^{-st}dt + \int_0^\infty\beta g(t)e^{-st} dt\] \[\alpha\int_0^\infty f(t)e^{-st}dt + \beta\int_0^\infty g(t)e^{-st} dt\] \[\alpha \mathcal{L}[f(t)] + \beta\mathcal{L}[g(t)]\]

위의 유도를 통해 라플라스 변환이 선형성을 가짐을 알 수 있습니다. 앞서 라플라스 변환이 미적분 방정식을 쉽게 풀 수 있게 해준다고 했는데, 바로 이 선형성이 미적분 방정식의 풀이에 큰 도움을 줍니다.

\[y'' + y' + y = \sin3t\]

예를 들어, 위의 함수가 있을 때 $y$가 어떤 형태일지 구하기가 정말 막막한데요, 양변에 라플라스 변환을 취하면 아래와 같습니다.

\[\mathcal{L}[y'' + y' + y] = \mathcal{L}[\sin3t]\] \[\mathcal{L}[y''] + \mathcal{L}[y'] + \mathcal{L}[y] = \mathcal{L}[\sin3t]\] \[\mathcal{L}[y''] + \mathcal{L}[y'] + \mathcal{L}[y] = \frac{3}{s^2 + 9}\]

위와 같이 정리하고 나니까 조금은 간단해진 모습입니다. 그런데 도함수의 라플라스 변환을 어떻게 해야하는 지가 문제입니다. 다행히도 도함수의 라플라스 변환은 간단하게 구할 수 있습니다.

도함수의 라플라스 변환

일계도함수의 라플라스 변환 공식 유도는 아래와 같습니다.

\[\mathcal{L}[f'] = \int_0^\infty f'(t)e^{-st}dt\] \[u' = f'(t)\] \[v = e^{-st}\]

부분적분을 통해 정리하면 아래와 같습니다.

\[\mathcal{L}[f'] = \int_0^\infty u'v \space dt\] \[\int_0^\infty u'v \space dt = [uv]^b_a - \int_a^buv'\] \[[uv]^b_a - \int_a^buv' = [f(t)e^{-st}]_a^b - \int_a^bf(t)\times(-s)(e^{-st})dt\] \[[f(t)e^{-st}]_a^b - \int_a^bf(t)\times(-s)e^{-st}dt = -f(0) + s\int_0^\infty f(t)(e^{-st})dt\] \[-f(0) + s\int_0^\infty f(t)(e^{-st})dt = s\mathcal{L}[f] - f(0)\]

따라서 일계도함수의 라플라스 변환은 아래와 같이 원시 함수의 라플라스 변환으로 표현됩니다.

\[\mathcal{L}[f'] = s\mathcal{L}[f] - f(0)\]

일계도함수의 라플라스 변환을 위와 같이 정리했는데, 더 확장해서 고계도함수의 라플라스 변환 공식은 아래와 같습니다(유도 과정은 일계도함수의 유도 과정을 연속해서 적용).

\[\mathcal{L}[{f^{(n)}}] = s^n\mathcal{L}[f] - s^{n-1}f(0) - s^{n-2}f'(0) - \ldots -f^{(n-1)}(0)\]

헤비사이드 부분분수 분해(Heaviside Method)

헤비사이드 부분분수 분해는 부분분수 분해를 할 때, 각 부분분수의 계수를 쉽게 구할 수 있게 해주는 일종의 도구입니다.

\[\frac{s^2 + s + 1}{(s-2)(s-1)(s^2 + 1)} = \frac{a}{s-2} + \frac{b}{s - 1} + \frac{cs + d}{s^2 + 1}\]

부분분수 분해는 위와 같이 통분된 형태를 각 인수를 분모로 하는 분수의 합, 차로 바꾸어 표현하는 것을 의미합니다. 왼쪽의 식을 오른쪽 식의 형태로 바꾸는 일은 생각보다 간단합니다. 이때 각 계수를 구할 때 헤비사이드 방법론을 사용합니다.

먼저 $a$를 구하기 위해 양 변에 $s-2$를 곱해줍니다.

\[\frac{s^2 + s + 1}{(s-1)(s^2 + 1)} = a + \frac{b(s-2)}{s - 1} + \frac{(cs + d)(s-2)}{s^2 + 1}\]

이제 위의 식에 $s=2$를 대입하면 $a$값을 쉽게 구할 수 있습니다.

\[\frac{7}{5} = a\]

$b$를 구하려면 다시 양 변에 $s-1$를 곱해주고 $s=1$을 넣어줍니다.

\[b = -\frac{3}{2}\]

$c$와 $d$를 구하는 것도 마찬가지로 양 변에 $s^2+1$를 곱해준 다음 $s = i$를 대입합니다.

\[c = \frac{1}{10}, \space\space\space\space\space\space\space\space\space\space d = -\frac{3}{10}\]

위와 같은 방식으로 부분분수의 계수를 구하는 방법을 헤비사이드 방법론이라고 합니다.

라플라스 변환을 통한 미분방정식 해결

\[y'' + y = \sin(2t)\] \[\text{initial condition: } y(0)=2, \space\space y'(0)=1\]

위의 예시 미분방정식을 라플라스 변환을 통해 풀어보겠습니다.

\[\mathcal{L}[y''] + \mathcal{L}[y] = \mathcal{L}[\sin 2t]\] \[s^2\mathcal{L}[y] - sy(0) - y'(0) + \mathcal{L}[y] = \mathcal{L}[\sin 2t]\] \[(s^2+1)\mathcal{L}[y] = 2s + 1 + \frac{2}{s^2+4}\] \[L[y] = \frac{2s + 1}{s^2 + 1} + \frac{2}{(s^2 + 1)(s^2 + 4)}\]

우변의 첫 번째 항의 두 분자를 나눠주고, 두 번째 항은 헤비사이드 부분분수 분해를 통해 나눠주면 아래와 같습니다.

\[L[y] = 2\frac{s}{s^2 + 1} + \frac{1}{s^2 + 1} + 2/3\frac{1}{s^2+1} - 2/3\frac{1}{s^2+4}\]

이어서 라플라스 역변환을 통해 원래 함수가 어떤 형태인지 구해봅니다.

\[L[y] = 2\frac{s}{s^2 + 1} + 5/3\frac{1}{s^2 + 1} - 1/3\frac{2}{s^2+4}\] \[y = 2\cos t + \frac{5}{3}\sin t - \frac{1}{3}\sin 2t\]

$s$ 이동정리(제1 이동정리)

라플라스 변환을 하면 $s$에 대한 함수로 바뀌게 됩니다. $s$ 이동정리란 라플라스 변환 이전의 식의 형태에 특정 지수 함수가 곱해지면 라플라스 변환 이후의 함수가 $s$축 상으로 특정 상수만큼이 이동한다는 관계에 대한 정리입니다.

\[\mathcal{L}[e^{at}f(t)] = F(s-a)\]

위의 수식이 바로 $s$ 이동정리입니다. 이게 왜 성립되는지는 아래에서 유도합니다.

\[\int_0^\infty(f(t)e^{at})e^{-st}dt\] \[\int_0^\infty f(t)e^{-(s-a)t}dt\] \[F(s-a)\]

너무 당연한 사실 같아도 보이는데, 라플라스 역변환을 통한 미분 방정식 풀이에 꽤나 큰 도움이 됩니다. 아래의 예시에서 $s$ 이동정리를 사용하는 방법을 살펴봅니다.

\[\mathcal{L}[y] = \frac{1}{s^2 - 6s + 10}\]

분자에 $1$이 있어서 $\sin$의 꼴로 정리될 것 같긴 한데, 명확하지는 않은 상태입니다. 이때 $s$ 이동정리를 사용합니다.

\[\frac{1}{s^2 - 6s + 10} = \frac{1}{(s-3)^2 + 1}\] \[\frac{1}{(s-3)^2 + 1} = F(s - 3)\] \[\mathcal{L}[e^{3t}\sin t] = F(s - 3)\] \[y = e^{3t}\sin t\]

단위계단함수로 구간별 함수 표현

간혹 구간별로 정의된 함수가 있습니다. 그런 함수들은 여러 함수 조각들을 이어붙이는 형태로 정의되는데요, 이런 식으로 표현된 함수는 라플라스 변환을 적용시키 조금 곤란합니다. 따라서 구간별로 정의된 함수를 하나의 함수로 표현하는 방법에 대해 알아봅니다.

\[u_c(t)\]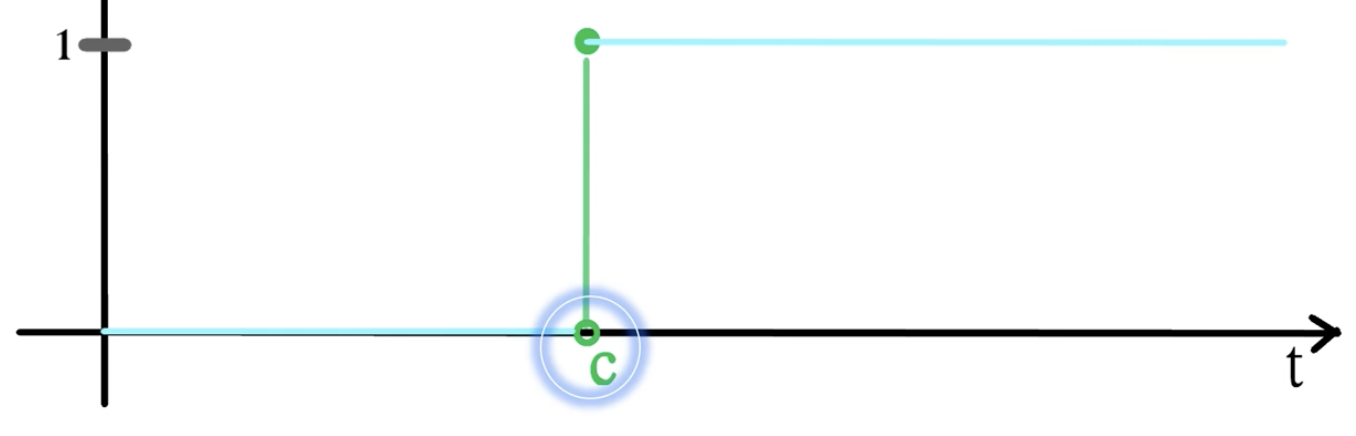

단위계단함수는 위와 같이 특정 상수 이상부터 함수 값이 0에서 1로 올라가는 형태를 가집니다. 이때 올라가는 크기가 1로 고정되기 때문에 ‘단위(Unit)’라는 말을 붙혀 표현합니다.

\[f(t) = \begin{cases} p(t) & \text{if } t \lt a \\ q(t) & \text{if } a \leq x \lt b \\ r(t) & \text{if } b \leq t \end{cases}\]

위의 함수는 단위계단함수를 통해 아래와 같이 정리됩니다.

\[f(t) = p(t)(1-u_a(t)) + q(t)(u_a(t) - u_b(t)) + r(t)\]

$t$ 이동정리(제2 이동정리)

갑자기 뜬근없이 왠 단위계단함수지? 싶은데, 이 단위계단함수가 라플라스 변환에서 유용한 $t$ 이동정리를 만들 때 사용됩니다.

\[\mathcal{L}[u_c(t)] = \int_0^\infty e^{-st}u_c(t)dt\] \[\int_0^\infty e^{-st}u_c(t)dt = \int_c^\infty e^{-st}dt\] \[\therefore \mathcal{L}[u_c(t)] = \frac{1}{s}e^{-cs}\]

단위계단함수의 라플라스 변환은 위와 같이 표현됩니다. 이어서 $t$ 이동정리에 대해 살펴봅니다.

\[\mathcal{L}[u_c(t)] = \frac{1}{s}e^{-cs}\] \[\mathcal{L}[f(t-c)u_c(t)] = \int_c^\infty f(t-c)e^{-st}dt\] \[\mathcal{L}[f(t-c)u_c(t)] = \int_0^\infty f(t)e^{-s(t+c)}dt\] \[\mathcal{L}[f(t-c)u_c(t)] = \int_0^\infty (f(t)e^{-st})(e^{-cs})dt\] \[\mathcal{L}[f(t-c)u_c(t)] = e^{-cs}\int_0^\infty (f(t)e^{-st})dt\] \[\mathcal{L}[f(t-c)u_c(t)] = e^{-sc}\mathcal{L}[f(t)]\]

위와 같이 기존 함수의 $t$축에 대한 이동과 라플라스 변환 이후의 식 사이의 관계를 표현할 수 있습니다. 이를 $t$ 이동정리라고 부릅니다.

주기함수 공식

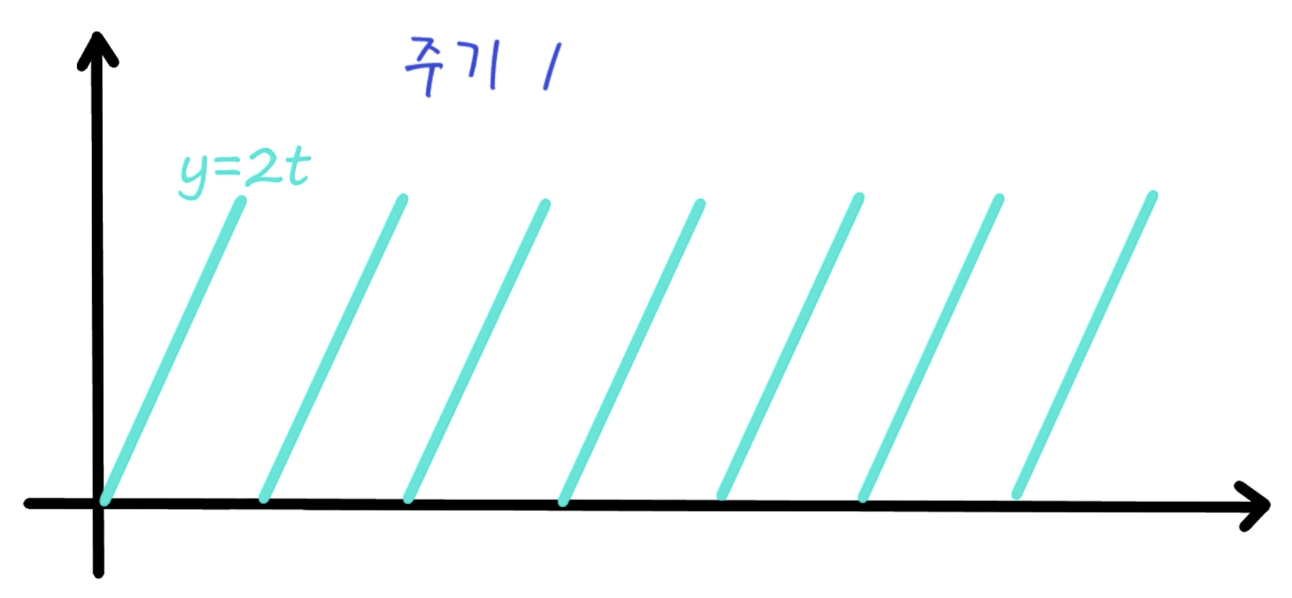
만약 위와 같은 주기함수가 있을 때 라플라스 변환 이후의 식은 어떤 형태일까요? 언뜻 생각하기에 $y=2t$의 라플라스 변환과 동일하지 않을까 싶지만 그렇지 않습니다. 아래에서 주기함수의 라플라스 변환이 어떻게 수행되는지 자세하게 살펴봅니다.

\[f(t + T) = f(t)\]

위는 주기함수의 공식입니다. 주기함수든 뭐든 라플라스 변환을 하기 위해서는 아래의 식을 계산해야 합니다.

\[\int_0^\infty e^{-st} f(t) dt\]

그런데 $f(t)$가 주기함수라면, 위 식과 주기만 적분한 식 사이에 관계식을 설정할 수 있겠다는 생각이 듭니다. 그 과정에서 주기함수의 특징을 이용해 식을 정리할 수 있을 것입니다. 그래서 단위계단함수를 사용해 아래와 같이 관계식을 얻을 수 있습니다.

\[\int_0^T e^{-st} f(t) dt = \int_0^\infty e^{-st} f(t)(1 - u_T(t)) dt\]

그런데 위 식의 우변을 다음과 같이 라플라스 변환 형태로 정리할 수 있습니다.

\[\int_0^\infty e^{-st} f(t)(1 - u_T(t)) dt = \mathcal{L}[f(t)(1 - u_T(t))]\] \[\mathcal{L}[f(t)(1 - u_T(t))] = \mathcal{L}[f(t)] - \mathcal{L}[f(t)u_T(t)]\]

위 식은 바로 전에 다룬 $t$ 이동정리에 의해 아래와 같이 변환됩니다.

\[\mathcal{L}[f(t)] - \mathcal{L}[f(t)u_T(t)] = \mathcal{L}[f(t)] - \mathcal{L}[f(t+T-T)u_T(t)]\] \[\mathcal{L}[f(t)] - \mathcal{L}[f(t)u_T(t)] = \mathcal{L}[f(t)] - e^{-Ts}\mathcal{L}[f(t+T)]\] \[\mathcal{L}[f(t)] - \mathcal{L}[f(t)u_T(t)] = (1-e^{-Ts})\mathcal{L}[f(t)]\] \[\int_0^T e^{-st}f(t)dt = (1-e^{-Ts})\mathcal{L}[f(t)]\]

따라서 주기함수에 대한 라플라스 변환 공식은 아래와 같이 정리됩니다.

\[\therefore \mathcal{L}[f(t)] = \frac{\int_0^T e^{-st}f(t)dt}{1-e^{-Ts}}\]

그러면 처음의 $y=2t$가 반복되는 주기함수는 아래와 같이 라플라스 변환을 할 수 있습니다.

\[\therefore \mathcal{L}[f(t)] = \frac{\int_0^1 e^{-st}2t \space dt}{1-e^{-s}} = -\frac{2e^{-s}}{s(1-e^{-s})} + \frac{2}{s^2}\]

라블라스 변환 합성곱 정리

신호처리나 인공지능 관련 과목을 들어봤다면 합성곱 연산에 대해 익숙할 텐데요, 합성곱 연산의 정확한 정의는 아래와 같습니다.

\[f(t) *g(t) = \int_0^tf(\tau)g(t-\tau)d\tau\]

라플라스 변환은 합성곱과 관련해 굉장히 신기한 성질이 있습니다. 그건 두 함수의 합성곱에 대한 라플라스 변환은 원시함수의 곱과 각각의 함수에 대한 라플라스 변환의 곱과 동일하다는 성질인데, 아래와 같이 정리할 수 있습니다.

\[\mathcal{L}[f(t)*g(t)] = F(s)G(s)\]

위의 성질을 어떻게 써먹을 수 있는지 간단한 예시와 함께 살펴봅니다.

\[\mathcal{L}^{-1}[\frac{s}{(s^2 + 1)^2}]\] \[\mathcal{L}^{-1}[\frac{1}{(s^2 + 1)} \times \frac{s}{(s^2 + 1)}]\]

이렇게 분해하고 나면 하나는 $\cos$의 라플라스 변환식이고 다른 하나는 $\sin$의 라플라스 변환식입니다. 따라서 아래와 같이 합성곱으로 표현할 수 있습니다.

\[\mathcal{L}^{-1}[\frac{2s}{(s^2 + 1)^2}] = \int_0^t \sin\tau \cos(t - \tau)d\tau\]

그리고 $\sin$과 $\cos$의 합성곱은 아래와 같이 간단하게 정리됩니다.

\[\int_0^t \sin\tau \cos(t - \tau)d\tau = \frac{t\sin t}{2}\]