CS231n: What is Needed to Build Deep Neural Networks 01

이 포스팅은 ‘CS231n의 Lecture 06‘에 대한 내용을 담고 있습니다.

자료 출처

• https://www.youtube.com/playlist?list=PL3FW7Lu3i5JvHM8ljYj-zLfQRF3EO8sYv
• https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture6.pdf

Deep Neural Networks

이전 포스팅에서는 Neural Networks가 무엇인지, 어떻게 여러 층을 쌓아 만들어지는지, 그리고 이미지 데이터를 효과적으로 처리하기 위한 CNN 구조까지 살펴보았습니다. 그런데 그렇게 배운 내용들만으로 이전 포스팅에서 만들었던 모델은 전혀 학습이 되질 않았습니다. 혹시 모델의 용량이 부족했을까요? 그렇지 않습니다. 동일한 5층짜리 이미지 분류기만으로도 충분히 75% 이상의 정확도를 낼 수 있습니다. 문제는 용량이 아니라 학습의 방향에 있습니다.

현재 모델 내부의 파라미터들을 아무런 제약 없이 학습시키고 있는데, 이렇게 그냥 아무런 제한 없이 학습을 시켜버리면 파라미터들이 이상한 값들로 수렴해버려 모델이 망가져버리게 됩니다.

따라서 모델이 더 안정적으로, 올바른 방향으로 학습될 수 있도록 여러 가지 가이드라인을 설치할 필요가 있습니다. 구체적으로 어떤 문제가 발생하는지, 또 그 친구들을 어떻게 해결할 수 있는지 하나하나 살펴봅시다.

Issue 01: Activation Function

\[\sigma (x) = \frac{1}{1+e^{-x}}\]

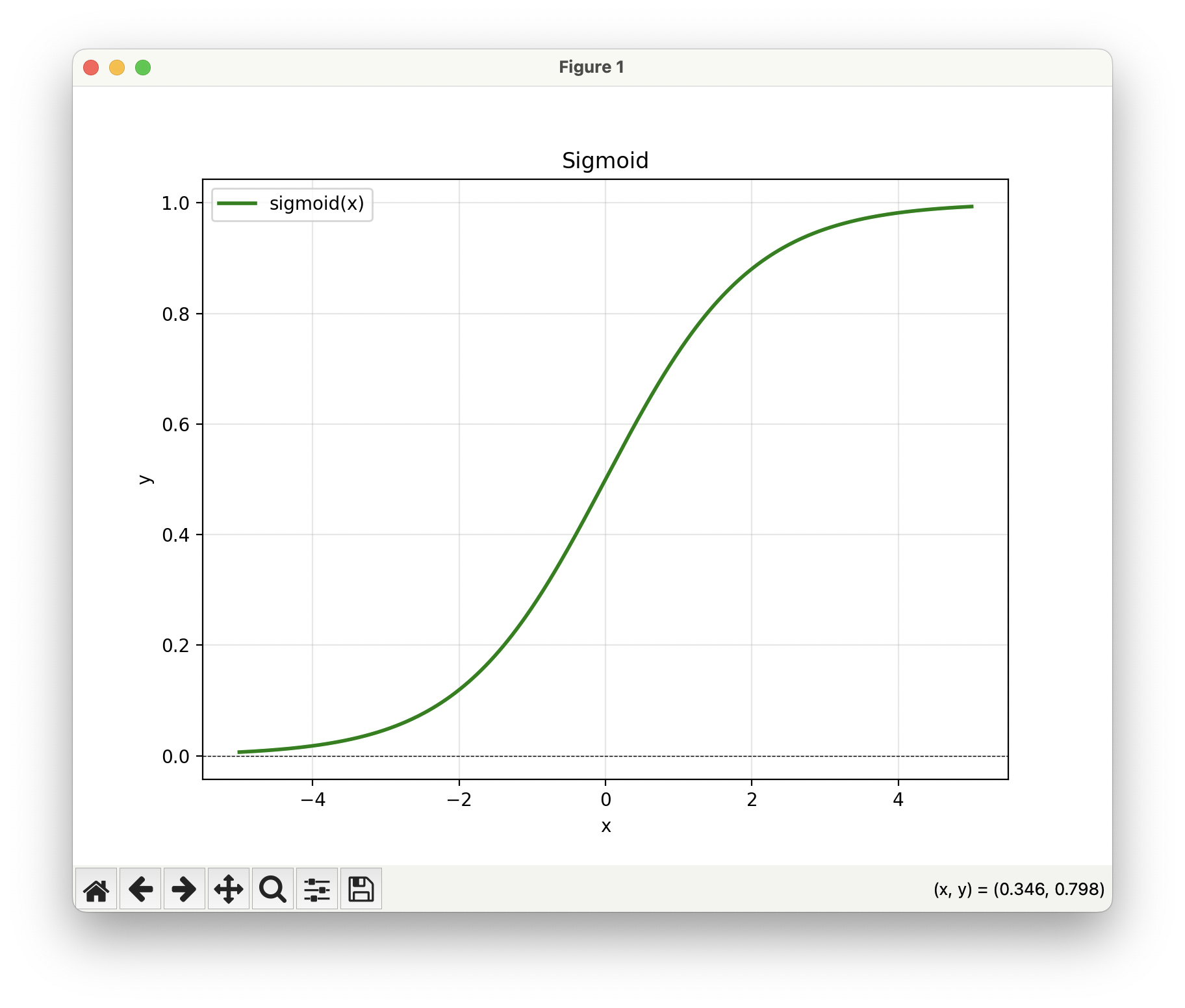
우리가 그동안 사용했던 Sigmiod 함수는 정말 인기가 많았습니다. 왜냐하면 이 함수의 모양이 뉴런을 표현할 때 좋은 해석을 제공했기 때문인데요, 보통 사람의 뉴런을 표현할 때 0 아니면 1로 이진 발화한다고 모델링하는 경우가 많거든요. 그러니까 뉴런이 자극을 받으면 그 다음 뉴런으로 자극을 전달하는 값이 있거나(1) 없거나(0) 둘 중 하나라고 모델링합니다. 그리고 또 결정론적으로 발화한다고 보지 않고 확률적으로(자극을 받은 경우에도 어떤 때에는 자극을 전달하지 않는 경우가 있을 수 있다는 거) 발화한다고 보기 때문에 0과 1 사이를 부드럽게 이어주는 이 함수를 뉴런이 발화할 확률이라고 사용하기 딱이었던 거죠. 그런데 그런 식의 해석의 용이성이 있다 뿐, 너무 많은 문제가 있습니다.

Gradient Vanishing(기울기 소실)

가장 첫번째로 모델이 깊어지면 깊어질수록 초반 레이어들에 전해지는 기울기가 급격하게 감소합니다. Sigmoid 함수의 가장 치명적인 문제점이기도 한데요, 3층짜리 인공 신경망 예시에서 그 구체적으로 살펴봅시다.

\[z^{[1]} = W^{[1]}x + b^{[1]}\] \[a^{[1]} = \sigma(z^{[1]})\] \[z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}\] \[a^{[2]} = \sigma(z^{[2]})\] \[z^{[3]} = W^{[3]}a^{[2]} + b^{[3]}\] \[\hat y = \sigma(z^{[3]})\] \[L = \text{MSE}(y, \hat y)\]

위 모델에서 첫 번째 층, 두 번째 층, 세 번째 층 파리미터에 대한 기울기를 구하기 위한 Chain Rule 식을 써보면 아래와 같습니다.

\[\frac{\partial L}{\partial W^{[3]}} = \frac{\partial L}{\partial \hat y} \cdot \underbrace{\frac{\partial \hat y}{\partial z^{[3]}}}_{\text{sigmoid}} \cdot \frac{\partial z^{[3]}}{\partial W^{[3]}}.\] \[\frac{\partial L}{\partial W^{[2]}} = \frac{\partial L}{\partial \hat y} \cdot \underbrace {\frac{\partial \hat y}{\partial z^{[3]}}} _{\text{sigmoid}} \cdot \frac{\partial z^{[3]}}{\partial a^{[2]}} \cdot \underbrace {\frac{\partial a^{[2]}}{\partial z^{[2]}}} _{\text{sigmoid}} \cdot \frac{\partial z^{[2]}}{\partial W^{[2]}}\] \[\frac{\partial L}{\partial W^{[1]}} = \frac{\partial L}{\partial \hat y} \cdot \underbrace {\frac{\partial \hat y}{\partial z^{[3]}}} _{\text{sigmoid}} \cdot \frac{\partial z^{[3]}}{\partial a^{[2]}} \cdot \underbrace {\frac{\partial a^{[2]}}{\partial z^{[2]}}} _{\text{sigmoid}} \cdot \frac{\partial z^{[2]}}{\partial a^{[1]}} \cdot \underbrace {\frac{\partial a^{[1]}}{\partial z^{[1]}}} _{\text{sigmoid}} \cdot \frac{\partial z^{[1]}}{\partial W^{[1]}}\]

초반 레이어로 가면 갈수록 이후 레이어들의 각 요소들에 대한 기울기가 계속 쌓여가는 것을 확인할 수 있죠. 바로 이 지점에서 문제가 발생합니다. 두 변수가 Sigmoid로 이어진 부분에 아래 중괄호로 표시를 해두었는데, 출력 지점을 기준으로 레이어를 거듭할수록 Sigmoid에 의한 기울기 요소가 1개씩 추가되죠. 문제는..

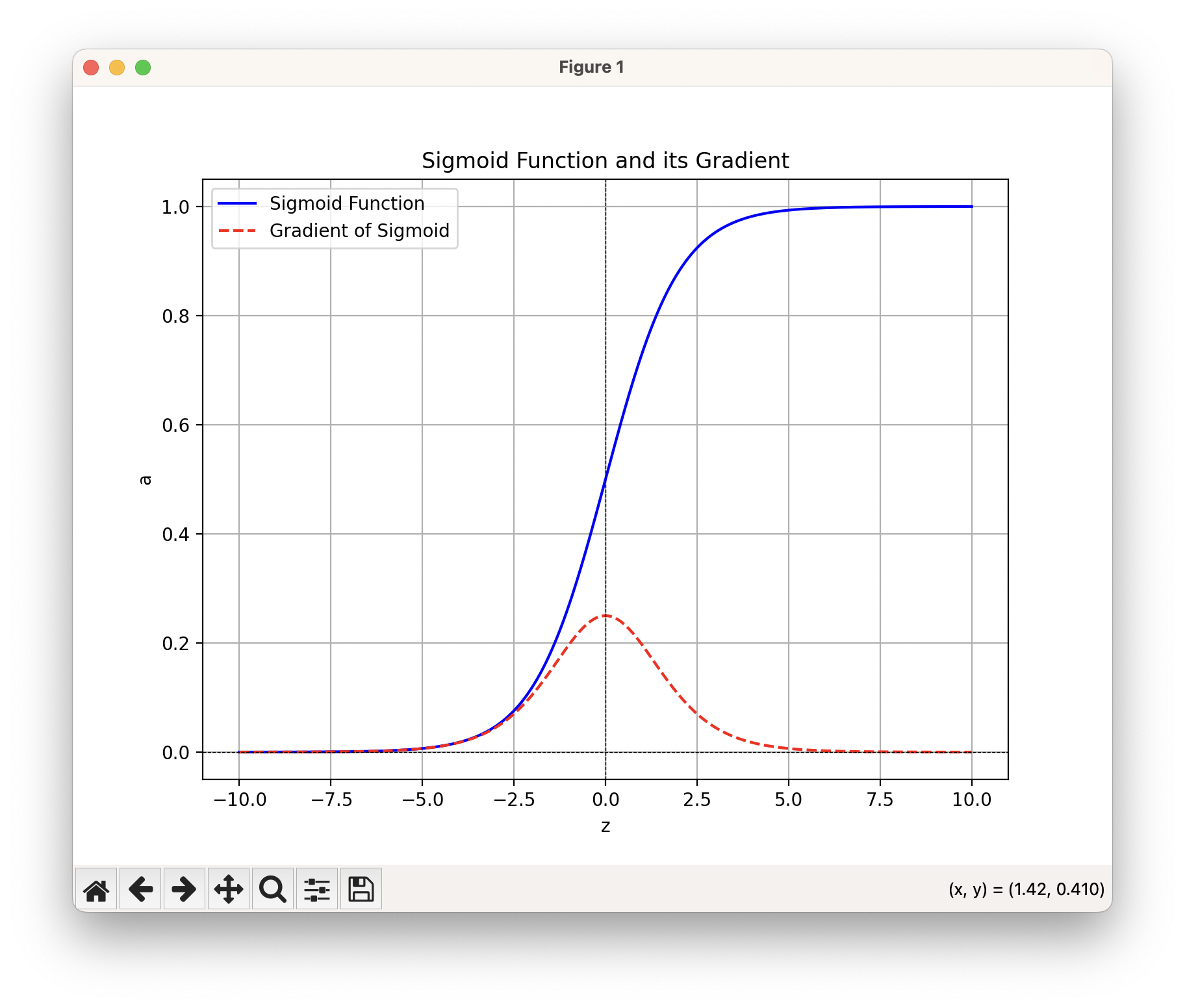
Sigmoid 함수의 모양입니다. Sigmoid 함수는 0일 때 기울기가 0.25로 가장 크고 입력의 절댓값이 5을 넘어서게 되면 기울기가 거의 0에 수렴합니다. 그러니까 $\frac{\partial a^{[.]}}{\partial z^{[.]}}$이 0과 0.25 사이의 어떤 값으로 구해지는데, 초반 레이어로 가면 갈수록 이 값이 Chain Rule에서 더 많이 곱해지므로 최종적으로는 초반 레이어의 파라미터들은 손실에 대한 기울기가 0.000… 의 아주 작은 값으로 나타납니다. 그 말인 즉, 초반 레이어에 있는 파라미터들을 당장 조금 움직여봤자, 전체 손실에는 전혀 변화를 주지 못한다는 말이 됩니다. Sigmoid를 사용하는 모델에서는 초반 레이어의 파라미터들이 예측 결과에 아무 영향도 주지 못하는 중요하지 않은 부분으로 전락해버린다는 의미일까요?

Sigmoid 실수 전 범위를 입력받아 0과 1 사이의 값을 출력하며, 특히 입력이 0 근처일 때 출력이 빠르게 변합니다. 이 함수를 층층이 반복해서 적용하면(여러 층의 Sigmoid를 쌓는 경우), 각 층의 포화가 누적되어 입력–출력 관계가 점점 완만한 S-곡선에서 계단(step) 함수처럼 급격히 넘어가는 형태로 바뀝니다. 이로 인해 피크(값이 급격하게 변하는 지점)를 제외한 넓은 plateau 구간에서는 기울기가 거의 0에 가까워져 파라미터가 거의 업데이트되지 않는 문제가 발생하게 됩니다. 구체적인 예시를 들어서 살펴봅시다.

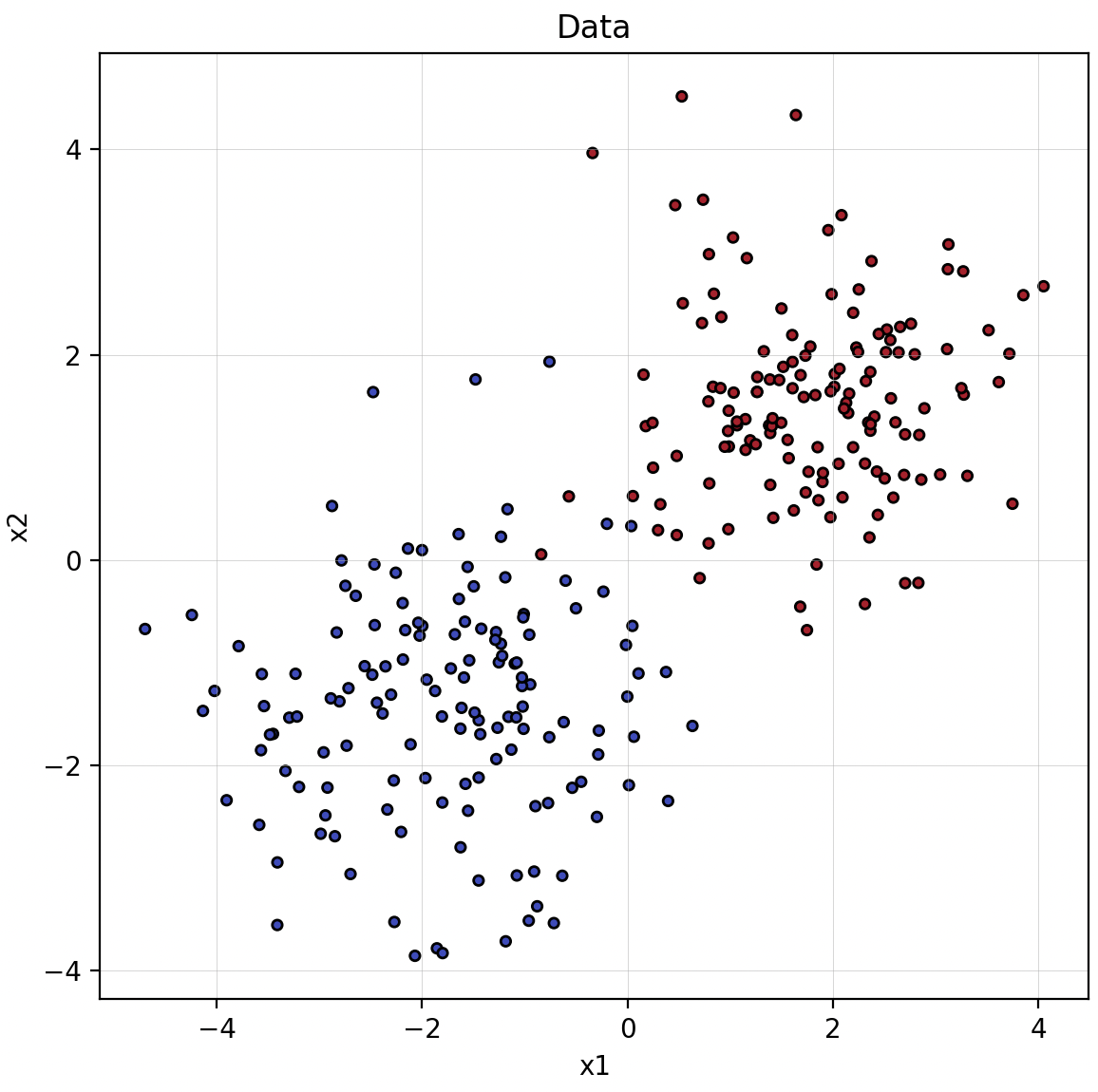
2차원 공간에 두 개의 군집 데이터를 생성하고, 이를 분류하기 위한 간단한 신경망을 구성합니다. 모든 레이어는 뉴런 2개짜리 FC-Layer으로 이루어지며, 활성화 함수는 Sigmoid를 사용합니다. 이제 2층 네트워크와 9층 네트워크를 각각 간단히 학습시킨 뒤, 학습된 상태에서 첫 번째 레이어의 두 뉴런에서 각각 선택한 가중치 하나($w_{0, 0}$, $w_{1, 0}$)를 축으로 하고 나머지 파라미터는 고정한 채 두 파라미터에 대해서만 손실이 어떻게 변하는지, 그러니까 $w_{0, 0}$, $w_{1, 0}$에 대한 손실평면을 구해보면요..

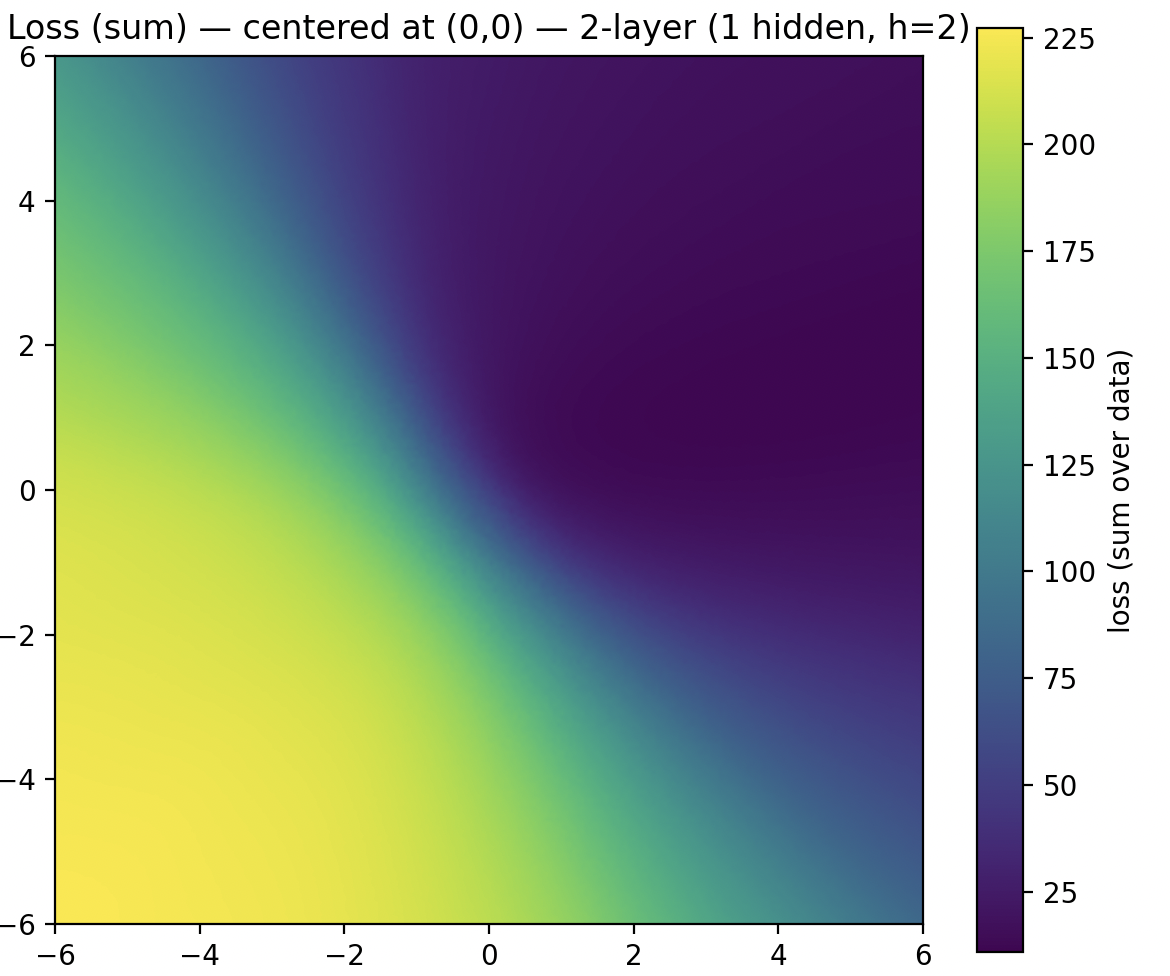
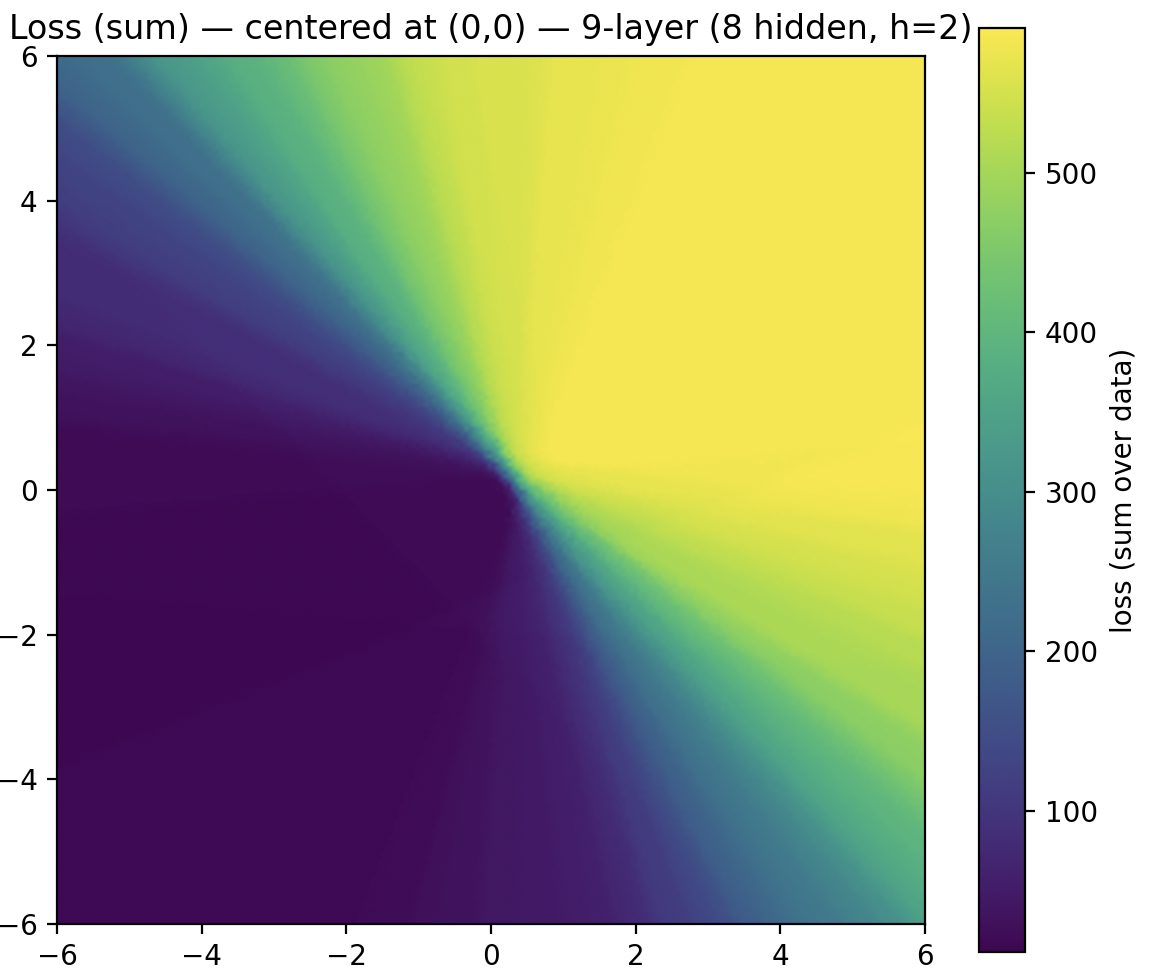
아주 극적인 차이는 아니지만 깊은 네트워크에서 손실 값이 바뀌는 구간이 더 날카롭게 드러나는 경향이 있는 것으로 보입니다. 이것을 기울기로 보면 차이가 더욱 분명해지는데요..

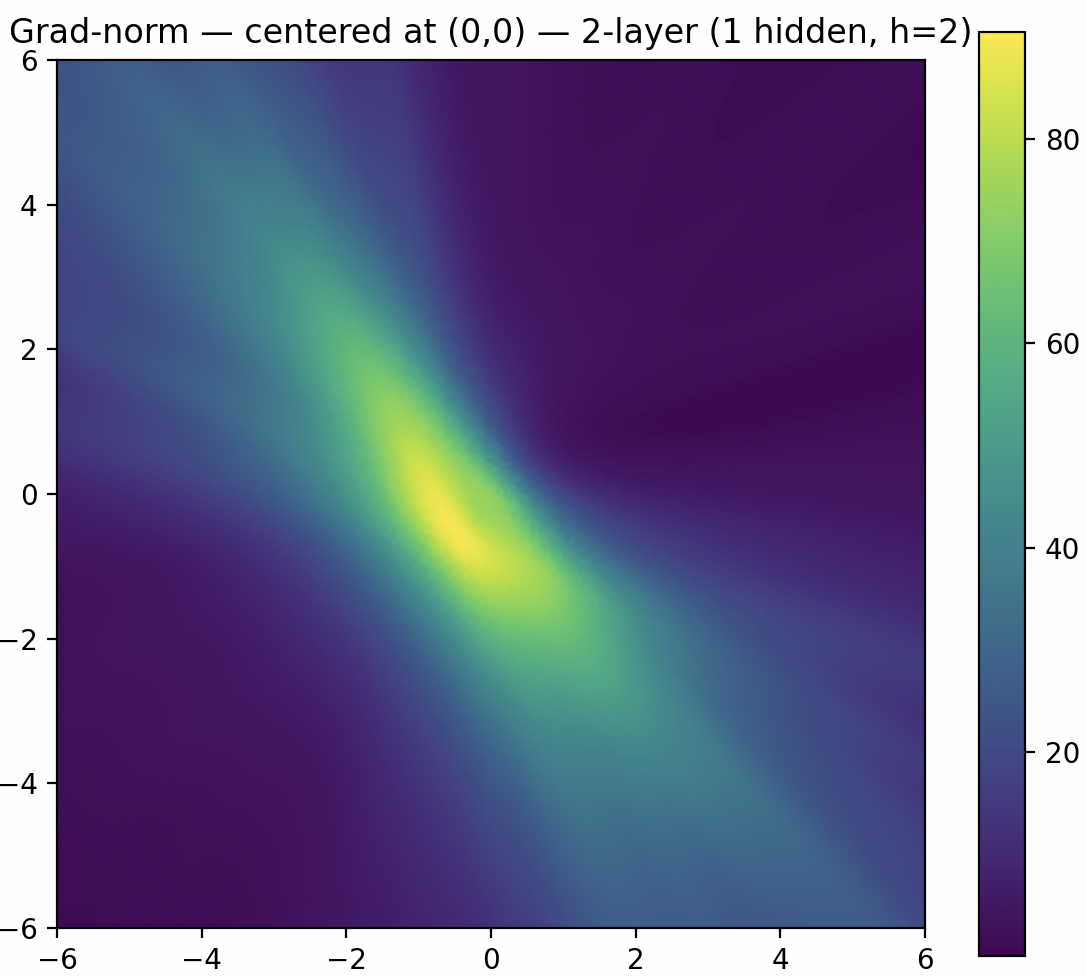
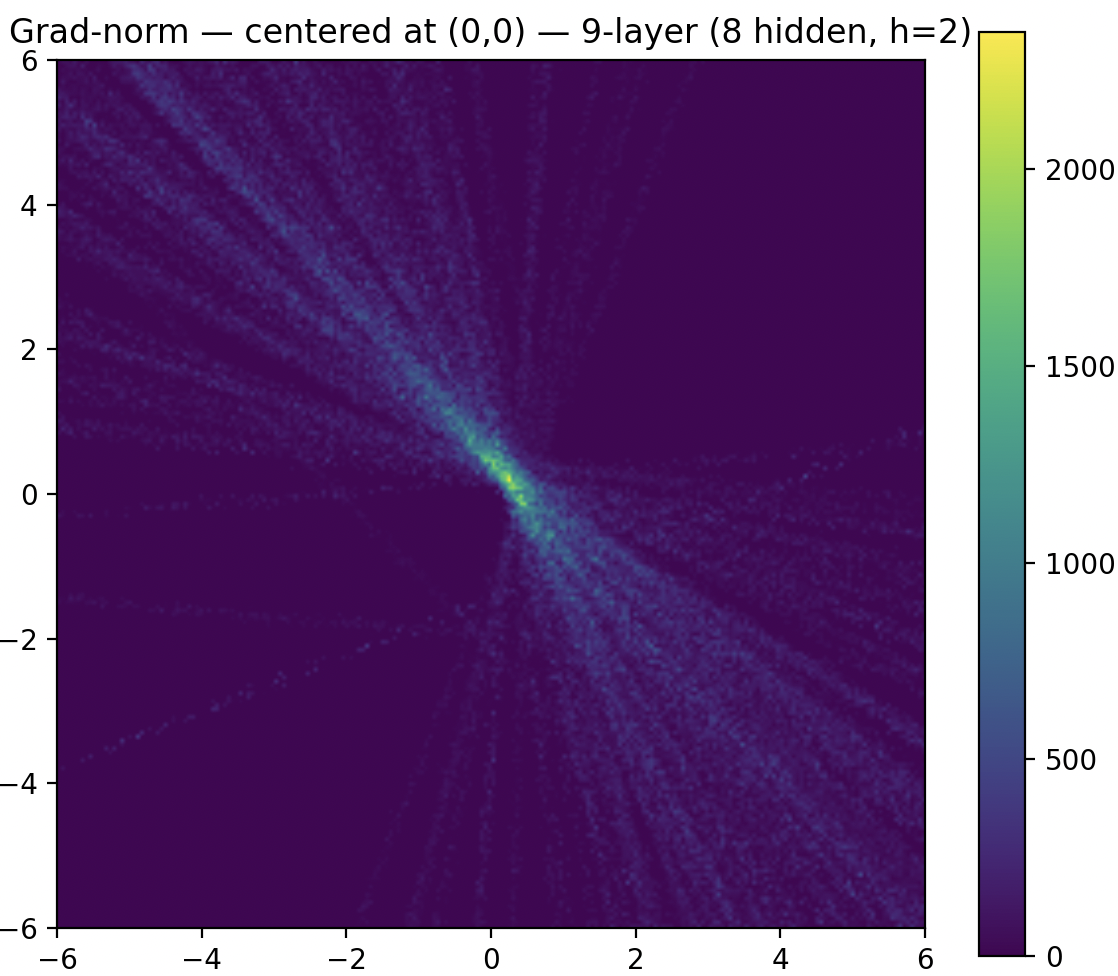
깊은 신경망에서는 첫 번째 레이어에 있는 두 파라미터의 기울기 피크 영역의 크기가 감소하지만, 피크의 세기는 커지는 것을 확인할 수 있습니다. 피크를 제외한 영역은 평탄(plateau)해서 조금 움직여도 손실이 거의 변하지 않습니다.

첫 번째 레이어의 파라미터들이 신경망에서 중요하지 않은 것이 아닙니다. 다만 신경망이 깊어질수록 손실이 변하는 구간이 좁아지고, 그 이외의 영역은 평탄해지기 때문에 작은 업데이트로는 손실의 변화를 일으키지 못하게 되는 문제 상황이 발생하게 되는 것이죠.

The Update Directions of The Weights are Identical

또 하나의 문제로 하나의 뉴런 내 가중치들의 업데이트 방향이 동일해진다는 점이 있습니다. 이게 무슨 말인지 아까 위의 3층짜리 신경망과 관련한 식에서 구체적으로 살펴봅시다.

\[\frac{\partial L}{\partial W^{[2]}} = \frac{\partial L}{\partial \hat y} \cdot {\frac{\partial \hat y}{\partial z^{[3]}}} \cdot \frac{\partial z^{[3]}}{\partial a^{[2]}} \cdot {\frac{\partial a^{[2]}}{\partial z^{[2]}}} \cdot \frac{\partial z^{[2]}}{\partial W^{[2]}}\]

두 번째 레이어의 가중치 행렬에 대한 기울기 식입니다. 행렬 단위로 기울기를 적어놓은 상태에서는 뭐가 문제인지 잘 보이지 않거든요? 위 식을 각 스칼라에 대한 식으로 바꿔쓰면..

\[\frac{\partial L}{\partial w^{[2]}_{ij}} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial z^{[3]}} \cdot \frac{\partial z^{[3]}}{\partial a^{[2]}_i} \cdot \frac{\partial a^{[2]}_i}{\partial z^{[2]}_i} \cdot \frac{\partial z^{[2]}_i}{\partial w^{[2]}_{ij}}\]

이렇게 표현됩니다. 위 식의 정확한 의미는 $w^{[2]}_{ij}$는 $i$번째 뉴런의 $j$번째 가중치 스칼라 값입니다. 그러니까 $i$번째 뉴런의 각 가중치에 대한 기울기는 아래와 같이 적히게 되죠.

\[\frac{\partial L}{\partial w^{[2]}_{i1}} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial z^{[3]}} \cdot \frac{\partial z^{[3]}}{\partial a^{[2]}_i} \cdot \frac{\partial a^{[2]}_i}{\partial z^{[2]}_i} \cdot \frac{\partial z^{[2]}_i}{\partial w^{[2]}_{i1}}\] \[\frac{\partial L}{\partial w^{[2]}_{i2}} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial z^{[3]}} \cdot \frac{\partial z^{[3]}}{\partial a^{[2]}_i} \cdot \frac{\partial a^{[2]}_i}{\partial z^{[2]}_i} \cdot \frac{\partial z^{[2]}_i}{\partial w^{[2]}_{i2}}\] \[\frac{\partial L}{\partial w^{[2]}_{i3}} = \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial z^{[3]}} \cdot \frac{\partial z^{[3]}}{\partial a^{[2]}_i} \cdot \frac{\partial a^{[2]}_i}{\partial z^{[2]}_i} \cdot \frac{\partial z^{[2]}_i}{\partial w^{[2]}_{i3}}\] \[\cdots\] \[\text{공통 부분: } \frac{\partial L}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial z^{[3]}} \cdot \frac{\partial z^{[3]}}{\partial a^{[2]}_i} \cdot \frac{\partial a^{[2]}_i}{\partial z^{[2]}_i}\]

그리고 $i$번째 뉴런의 각 가중치들은 위의 공통 부분을 가집니다. 이 공통 부분의 값은 양수 또는 음수겠죠. 동일 뉴런의 각 가중치에 대한 기울기는 공통 부분을 제외한 가장 마지막 항에 의해서만 차이가 발생합니다. 그런데 가장 마지막 항은 항상 양수 값으로 나오게 되고 이로 인해 동일 뉴런의 모든 파라미터의 기울기가 모두 양수이거나 모두 음수를 가리키게 됩니다.

가장 마지막 항이 왜 항상 양수일까요?

\[Z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}\] \[z^{[2]}_i = W^{[2]}_ia^{[1]} + b^{[2]}_i\] \[z_i^{[2]} = w_{i1}^{[2]}a^{[1]}_1 + w_{i2}^{[2]}a^{[1]}_2 + w_{i3}^{[2]}a^{[1]}_3 + \cdots + w^{[2]}_{ij}a_j^{[1]} + \cdots + w_{in}^{[2]}a^{[1]}_n + b^{[2]}_i\]

위 식에서 편미분을 하면,

\[\frac{\partial z^{[2]}_i}{\partial w^{[2]}_{ij}} = a_j^{[1]}\]

가 되고, $a_j^{[1]}$는 이전 레이어의 출력값으로 마지막에 Sigmoid를 거치기 때문에 항상 0과 1 사이의 양수 값을 가집니다. 따라서 $i$번째 뉴런의 모든 파라미터는 같은 기울기 방향을 가지게 되죠. 이게 문제가 되는 이유는…

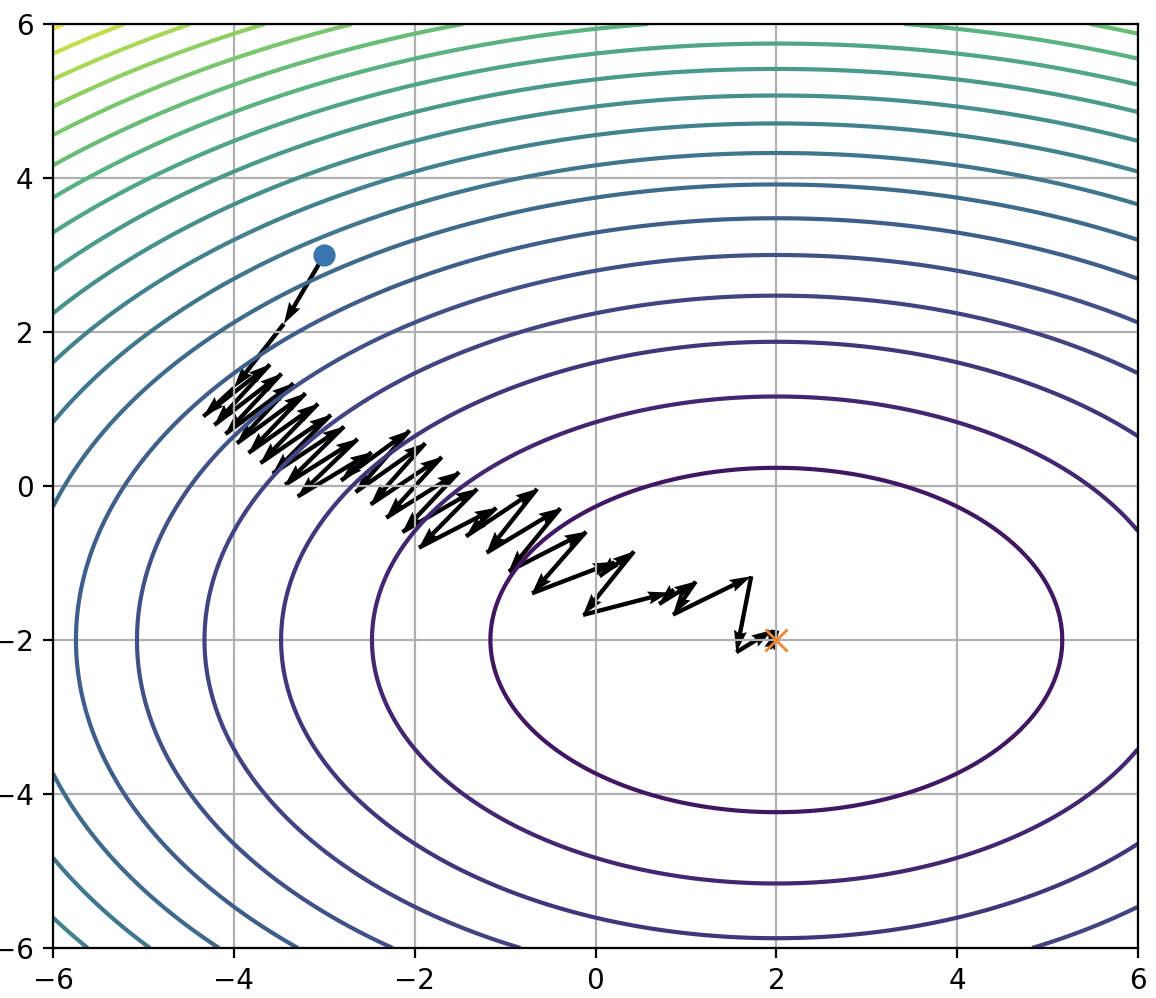
파라미터가 최적화되는 경로의 제약이 발생한다는 점에 있습니다. 위 예시처럼 한 뉴런 내의 두 가중치($w_{2,1}$, $w_{2,2}$)에 대해 손실 평면이 볼록(Convex)이고, 초기점이 최적점(4사분면)의 왼쪽 위에 있을 때를 생각해봅시다. Sigmoid를 사용하는 신경망에서는 같은 뉴런의 가중치의 기울기가 항상 동일하게 나온다고 했으니 위와 같이 업데이트 방향은 오른쪽 위 또는 왼쪽 아래로만 이루어집니다. 이 부호 제약 때문에 최적점으로 곧장 내려가는 가장 가파른 하강 방향을 따라가기 어렵고, 경로가 지그재그로 늘어나 불필요하게 많은 스텝을 밟게 됩니다. 이 문제는 Sigmoid가 항상 양수 값을 내뱉는 함수이기 때문에 발생합니다.

Solution

Sigmoid의 문제점은 2개로 요약할 수 있습니다. 첫째, 함수의 기울기 범위가 $(0, 0.25)$이기 때문에 Gradient Vanishing이 발생합니다. 둘째, 함수의 출력이 $(0, 1)$으로 항상 양수여서 파라미터가 비효율적으로 업데이트가 수행됩니다. 활성화 함수의 주된 목적은 레이어 사이에 비선형성을 추가해 각 레이어가 서로 다른 역할을 수행할 수 있도록 만드는 것입니다. 사실 활성화 함수가 비선형적이기만 하면 기본 목적은 달성되거든요? 그러니까 다양한 비선형 함수들 중, 앞서 언급한 두 가지 문제를 해결할 수 있는 적당한 대안 함수가 필요합니다.

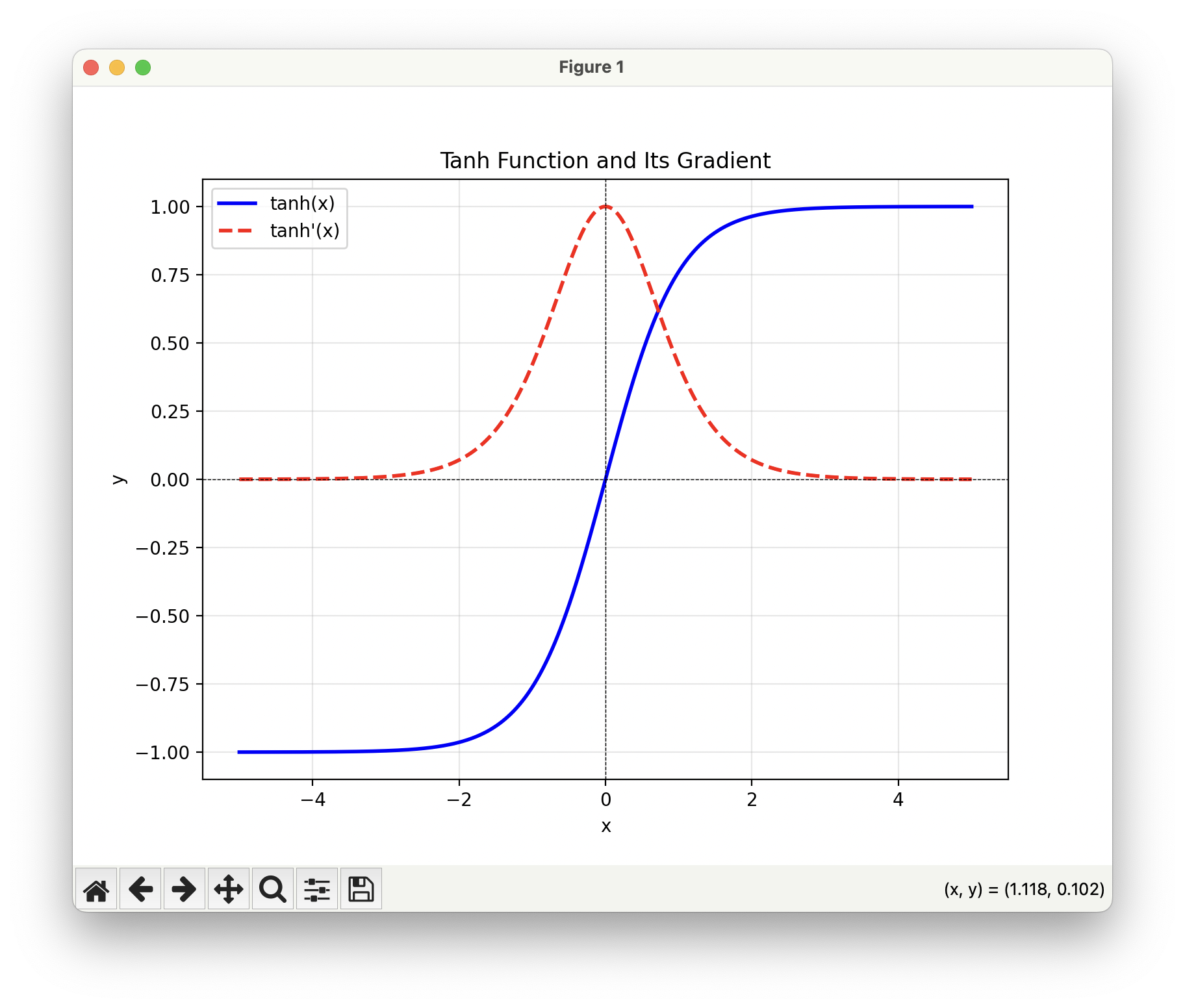
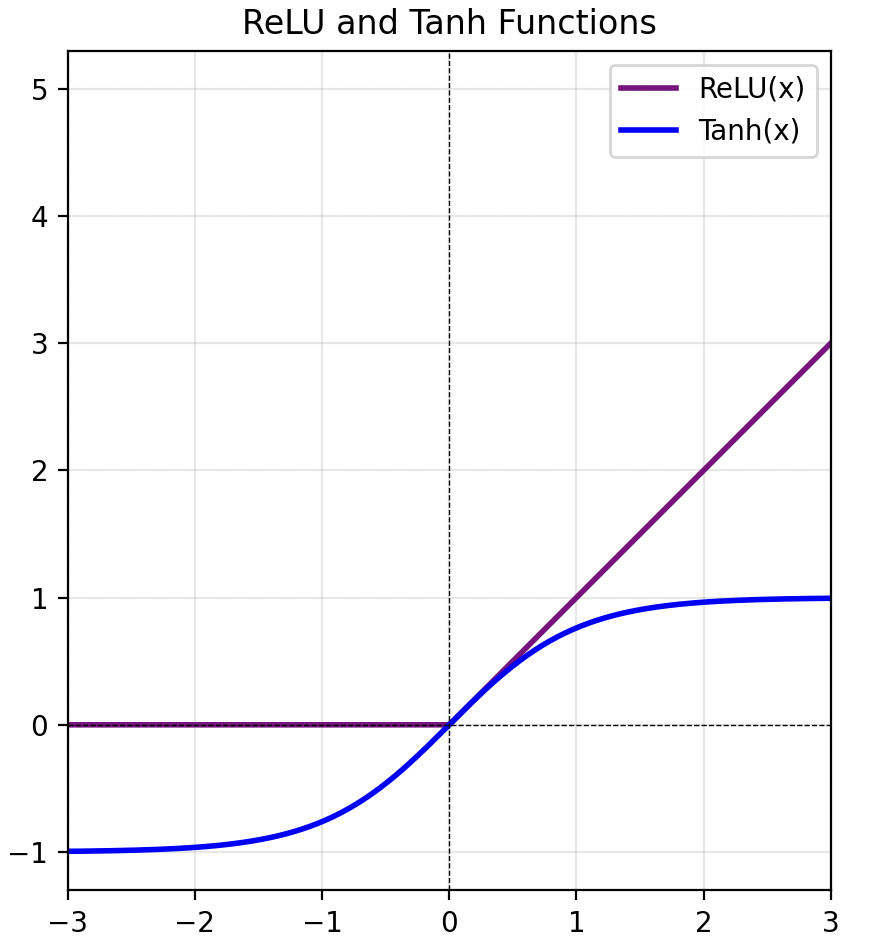
그래서 제안된 것이 tanh(hyperbolic tangent) 함수입니다. tanh는 Sigmoid와 유사한 S자 곡선 모양을 가지면서도, 기울기의 범위가 더 넓고 출력 값 역시 $(−1,1)$ 범위로 양수와 음수가 모두 포함됩니다. 따라서 Sigmoid의 단점을 상당 부분 개선할 수 있습니다. 하지만 tanh 역시 기울기가 1보다 작은 값을 가지기 때문에, 레이어를 많이 쌓으면 결국 초반 레이어에 있는 모든 파라미터들의 Gradient가 0에 가까워지는 Gradient Vanishing 문제가 여전히 발생합니다.

\[\text{ReLU}(x) = \max(0, x)\]

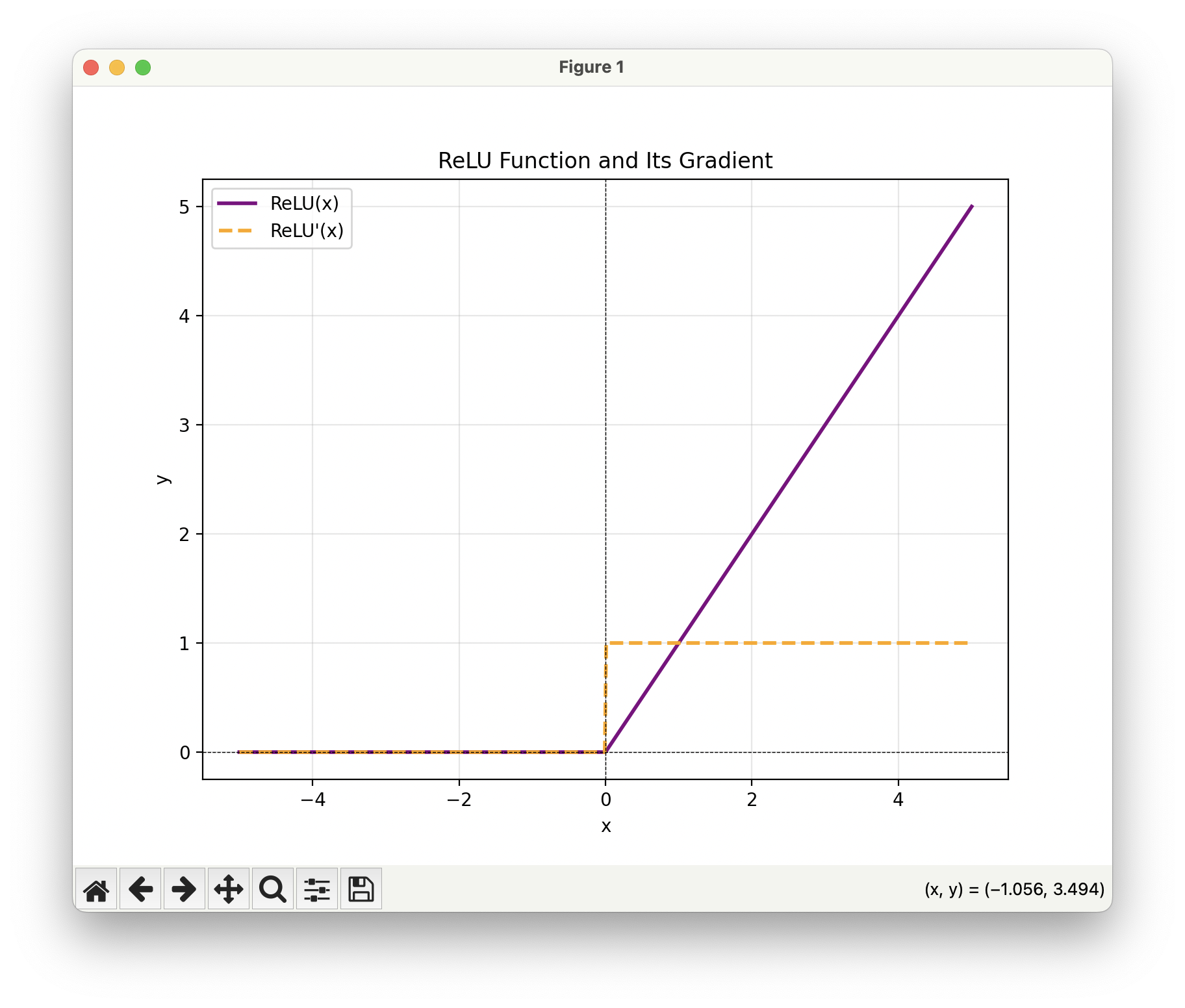
그렇게 다음에 제안된 함수가 지금도 사용되는 위의 ReLU(Rectified Linear Unit)입니다. ReLU는 위의 수식으로 정의되는데, 입력이 양수일 경우 그 값을 바로 출력하고 음수인 경우 0을 출력합니다. 기울기로 보면 양수일 때는 1, 음수일때는 0이 됩니다. 되게 단순한 구조에도 불구하고 기존 활성화 함수들의 문제점들 중 특히 가장 치명적이었던 Gradient Vanishing 문제를 해결합니다. 양수 영역에서는 기울기가 항상 1이기 때문에, 여러 층을 거치더라도 기울기의 크기가 줄어들지 않고 유지되죠. 또, 지수 연산이 필요한 Sigmoid나 tanh와 달리 단순한 max 연산만 사용하기 때문에 계산 효율성이 매우 높고 실제로 수렴 속도도 약 6배 정도 더 빠릅니다. 게다가 Sigmoid에 비해 생물학적 뉴런의 발화 특성을 훨씬 더 잘 모사한다는 점에서도 장점이 있죠.

당연히 장점만 있는 것은 아닌데요, 가장 대표적인 것이 Dead ReLU 문제입니다. ReLU는 음수 입력에 대해 항상 0을 출력하기 때문에, 이 영역에서 기울기가 0이 됩니다. Chain Rule로 미분을 전파할 때 0이 한 번이라도 포함되면 해당 뉴런의 파라미터 기울기는 완전히 사라져버리죠. 이 현상은 뉴런 단위로 발생하는데, 특정 뉴런의 ReLU 활성화함수로의 입력 스칼라 값이 음수로 나오면 해당 뉴런의 모든 가중치에 대해 학습이 이루어지지 않게 됩니다. 이를 방지하기 위해 ReLU를 사용할 때는 가중치 초기화 시 0.01과 같은 작은 양수를 더해, 뉴런이 처음부터 너무 쉽게 죽지 않도록 하는 방법을 쓰기도 합니다. 또 다른 한계로 ReLU의 출력 역시 Sigmoid와 동일하게 양수 범위를 갖기 때문에 파라미터 업데이트가 비효율적으로 이루어진다는 문제가 있습니다.

\[\text{Leaky ReLU}(x) = max(\alpha x, x); \space\space\space \alpha \approx 0.01\] \[\text{ELU}(x) = \begin{cases} x, & \text{if } x > 0 \\ \alpha \, (\exp(x) - 1), & \text{if } x \leq 0 \end{cases}\]

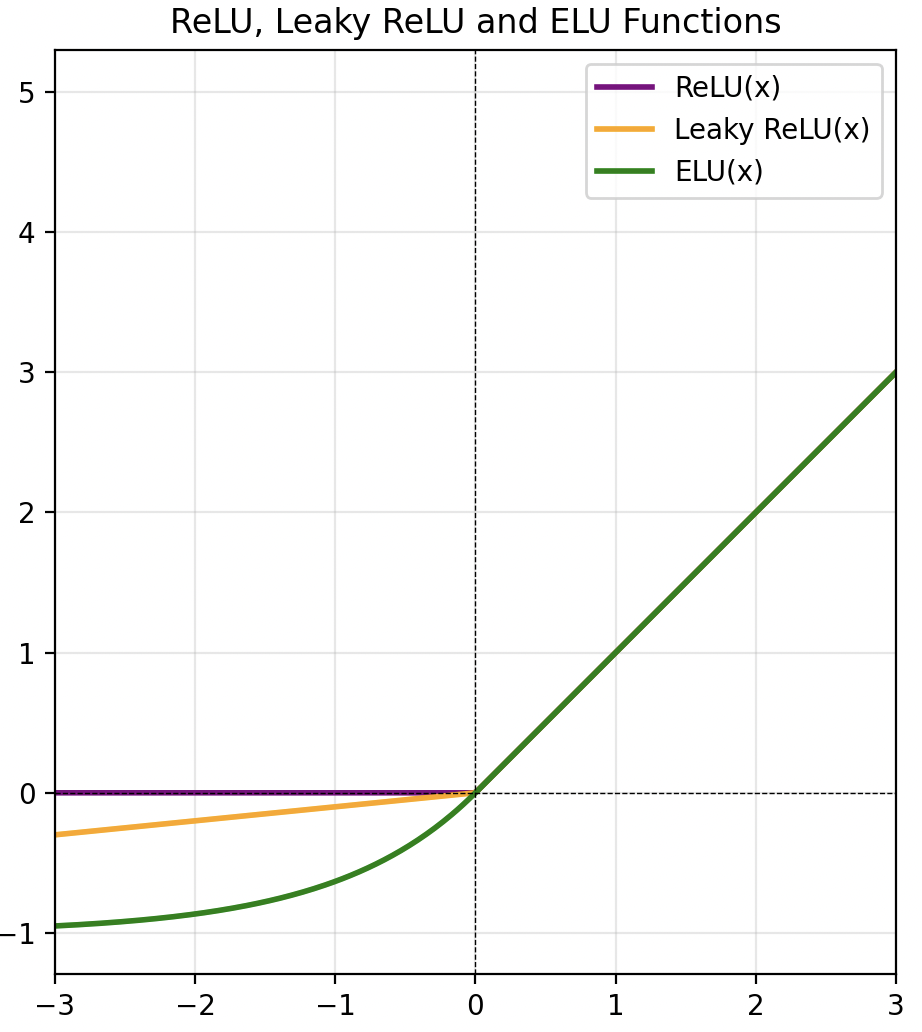
이러한 한계를 보완하기 위해 ReLU의 음수 영역을 변형한 여러 변형 함수들이 제안되었습니다. 대표적으로 Leaky ReLU와 ELU가 있습니다. 이 함수들은 음수 영역에 대해 단순히 0으로 고정하지 않고, 작은 기울기를 부여하여 Dead ReLU 문제를 완화합니다. 다만 실제로는 이런 변형 함수들이 널리 쓰이지는 않습니다. 이유는 충분히 깊은 신경망에서는 Dead ReLU가 그렇게까지 치명적인 문제를 일으키지 않기 때문인데요, 오히려 일부 뉴런이 죽으면서 발생하는 계산량 감소로 인한 이득이 더 큰 경우가 많습니다. 때문에 CNN 계열 네트워크에서는 여전히 기본 활성화 함수로 ReLU를 사용합니다.

\[\text{GELU}(x) = x \cdot \Phi(x) = x \cdot \frac{1}{2} \left[ 1 + \text{erf}\!\left(\frac{x}{\sqrt{2}}\right) \right]\]

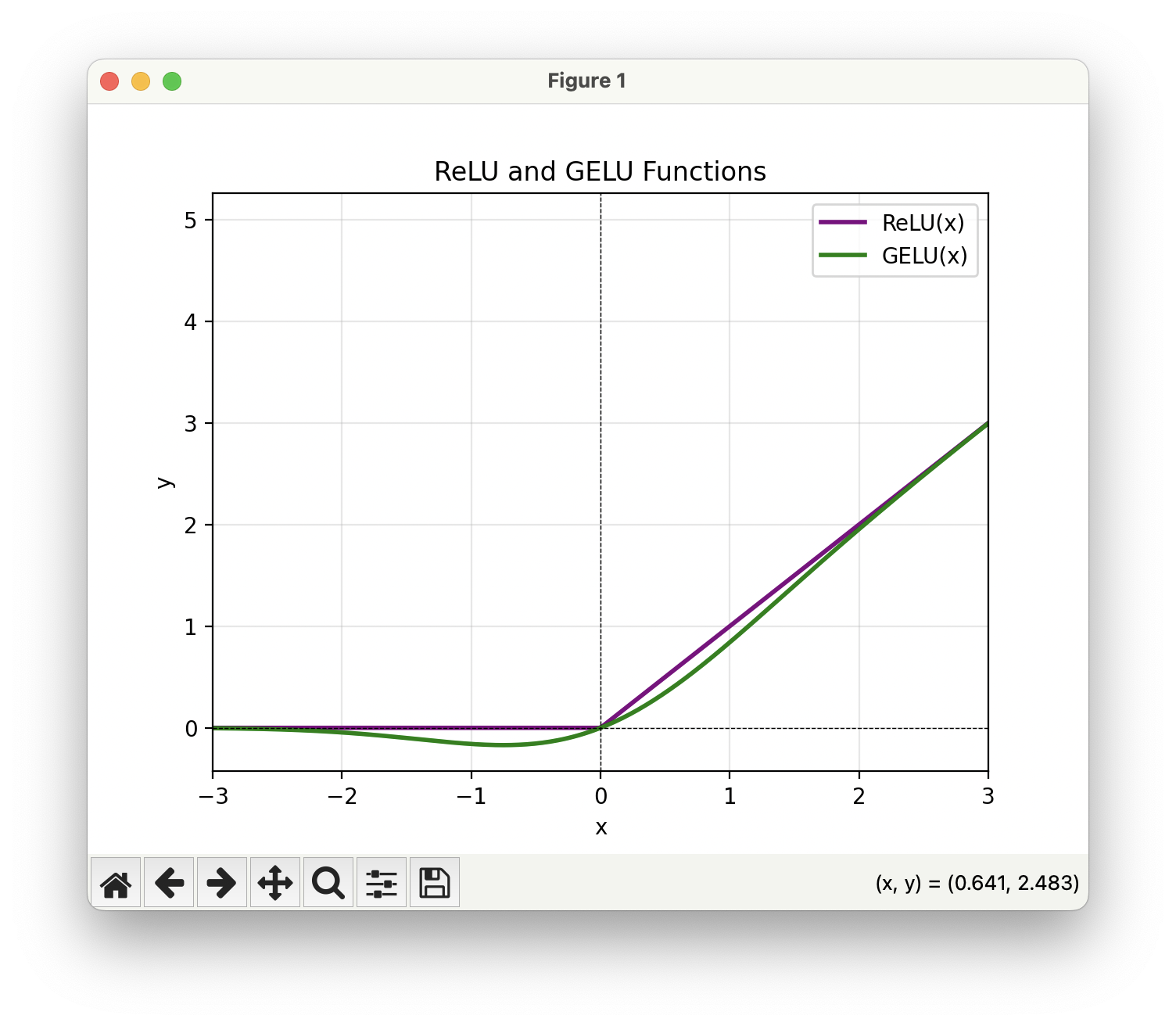
다만, 위의 GELU(Gaussian Error Linear Unit)만은 ReLU 계열 변형 중 현재까지도 널리 사용됩니다. Transformer 계열 모델에서는 사실상 표준으로 자리잡았는데, 오늘날 가장 널리 쓰이는 딥러닝 모델들이 Transformer 기반인 만큼 GELU 역시 현대 딥러닝의 기본 활성화 함수로 자리 잡았다고 할 수 있죠.

Issue02: Data Preprocessing(데이터 전처리)

시그모이드의 단점 중 하나는 출력이 항상 양수라서 역전파 시 같은 뉴런의 가중치들에 대해 기울기 부호가 동일해지게 되고, 결과적으로 업데이트 방향이 제한된다는 점이었죠. 첫 번째 레이어에서도 입력 이미지의 픽셀 값이 모두 양수인 경우 업데이트 방향이 제한되는 동일한 문제가 발생합니다. 따라서 입력의 평균이 0이 되도록 맞춰주는 작업이 필요합니다.

크게는 두 가지 방식이 있는데, 하나는 전체 평균 이미지를 구하는 방식입니다. 데이터셋 전체의 평균 이미지를 구해서 전체 데이터에 빼줍니다. 다른 방식으로는 채널별 평균을 빼주는 방법도 있습니다. 각 채널별로 스칼라 평균 값을 구하고 이를 빼줍니다. 방법 자체가 되게 가볍고 이미지 데이터가 여러 모양으로 존재하는 경우에도 사용하기 쉬워서 보통 자주 사용됩니다.

이 외에도 분산을 맞춰주는 정규화 작업을 수행할 수도 있는데, 이미지의 경우 보통 거기거 거기의 분포를 가지기 때문에 정규화가 꼭 필요하지는 않습니다.

Issue03: Weight Initialization(가중치 초기화)

다음으로 신경망의 가중치를 어떻게 초기화해야 하는지 살펴봅시다. 그냥 아무 값으로 시작하면 되지 않나..? 싶지만 깊은 신경망에서는 그렇게 했다가 큰 문제가 생깁니다. 예를 들어 tanh를 활성화 함수로 쓰는 경우를 기준으로 생각해봅시다. 가장 먼저 떠오르는 단순한 방법은 모든 가중치를 0으로 초기화하는 겁니다. 처음엔 0이라도 학습하면서 적절한 값으로 가겠지 하는 순진한 가정이죠. 하지만 모든 값을 0(0이 아니더라도 모두 동일한 값)으로 두면 치명적인 문제가 생깁니다. 바로 대칭성이 깨지지 않는다는 점입니다.

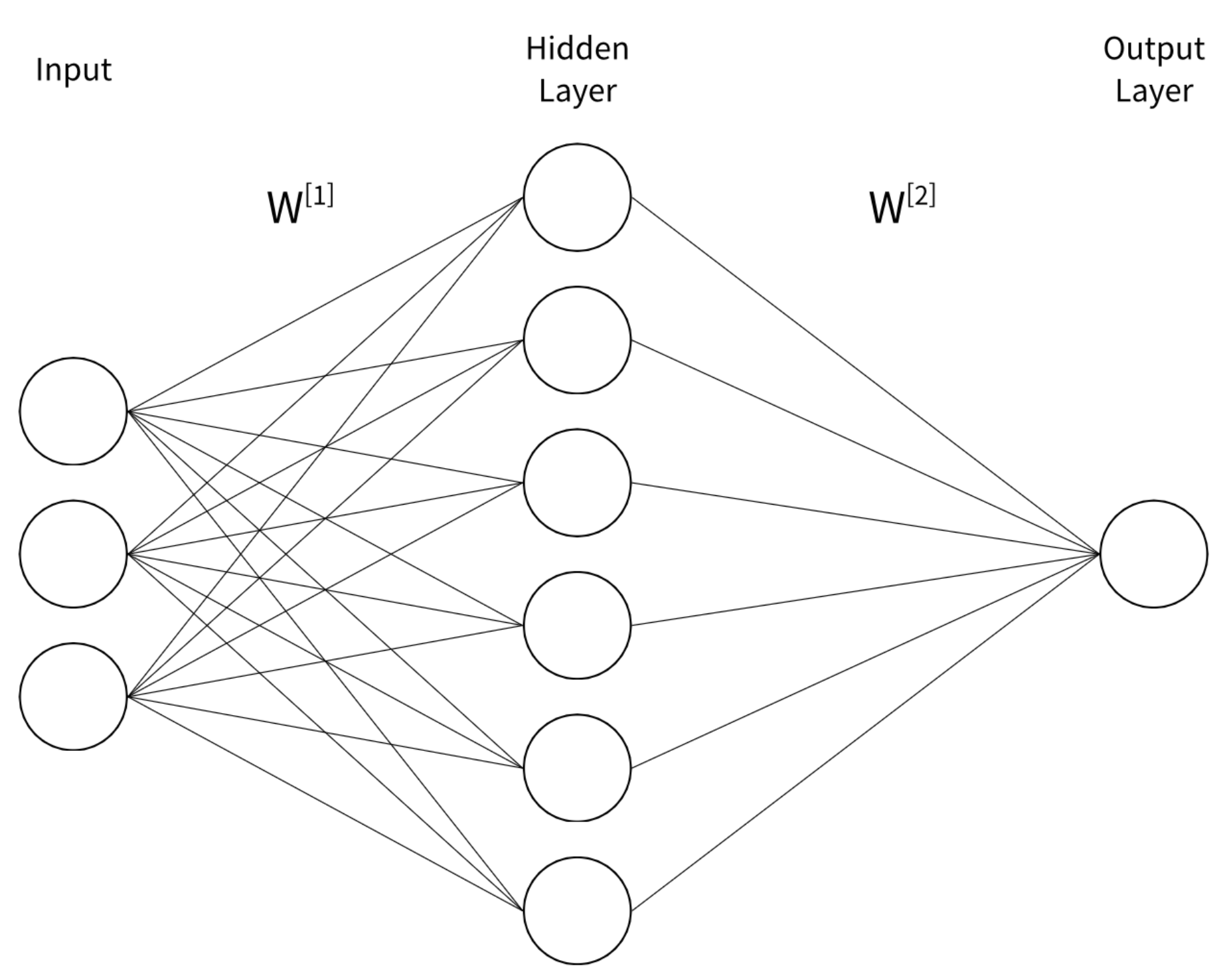
MLP의 각 뉴런은 기본적으로 이전 레이어의 모든 출력을 입력으로 받기 때문에 구조적으로 대칭적입니다. 이때 모든 레이어의 파라미터를 0 같은 동일한 값으로 맞추면, 예측값은 0이 되고 정답은 0이 아닐테니까 손실과 기울기는 생깁니다. 문제는 모든 뉴런이 같은 출력을 내니 같은 기울기를 받고 같은 양만큼 업데이트된다는 겁니다. 이 과정이 반복되어도 한 레이어 내 모든 뉴런이 항상 같은 업데이트를 수행해 대칭성이 유지됩니다. 우리가 여러 뉴런을 사용하는 이유가 각각의 뉴런이 서로 다른 특징에 집중해 좀 더 다양하고 많은 특징들을 사용하게 하기 위함인데, 이렇게 모두 동일하게 학습되면 당연히 성능이 좋지 않게 되겠죠.

\[W \sim \mathcal{N}(0, 1) \times0.01\]

그래서 모든 값을 0으로 두는 대신, 보통 평균 0, 표준편차가 작은 정규분포에서 가중치를 무작위로 뽑습니다. 이렇게 하면 처음부터 파라미터들 사이에 차이가 생겨 서로 다른 방향으로 업데이트되고, 뉴런들도 각자 다른 특징에 집중하도록 분화됩니다. 꽤 괜찮은 전략이지만, 레이어를 깊게 쌓으면 또 다른 문제가 나타납니다.

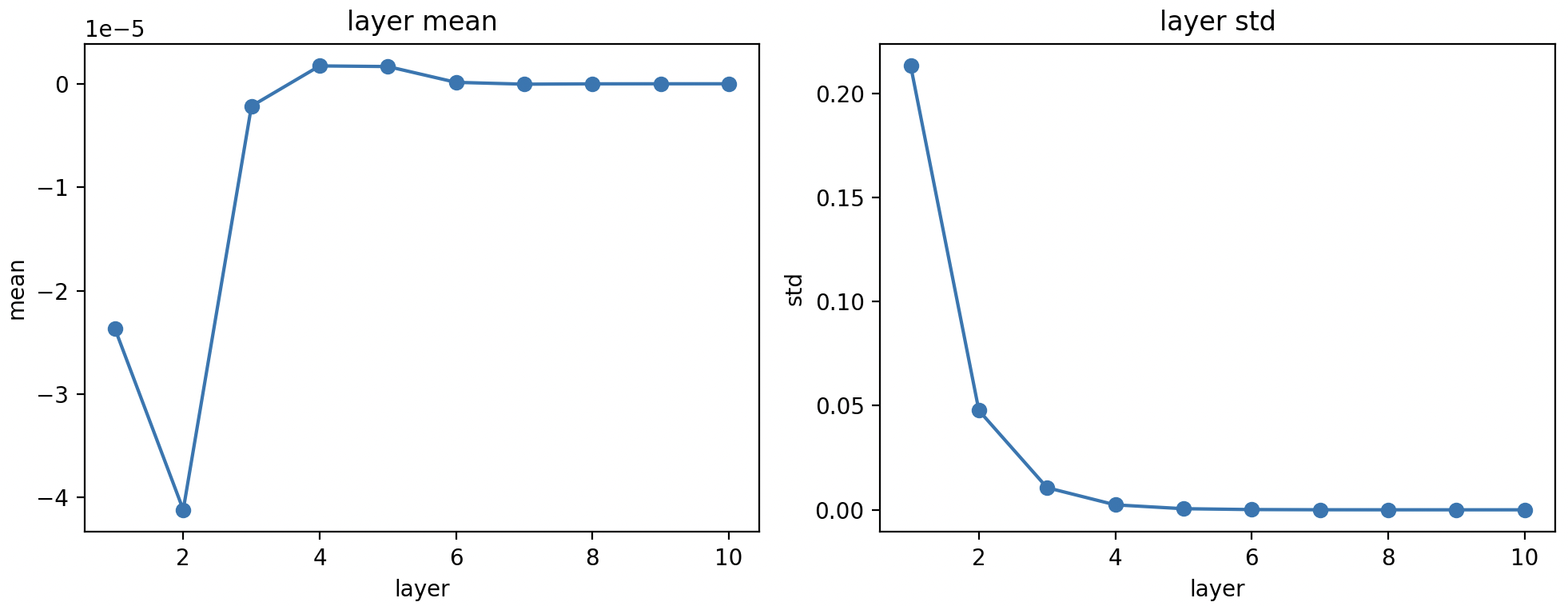
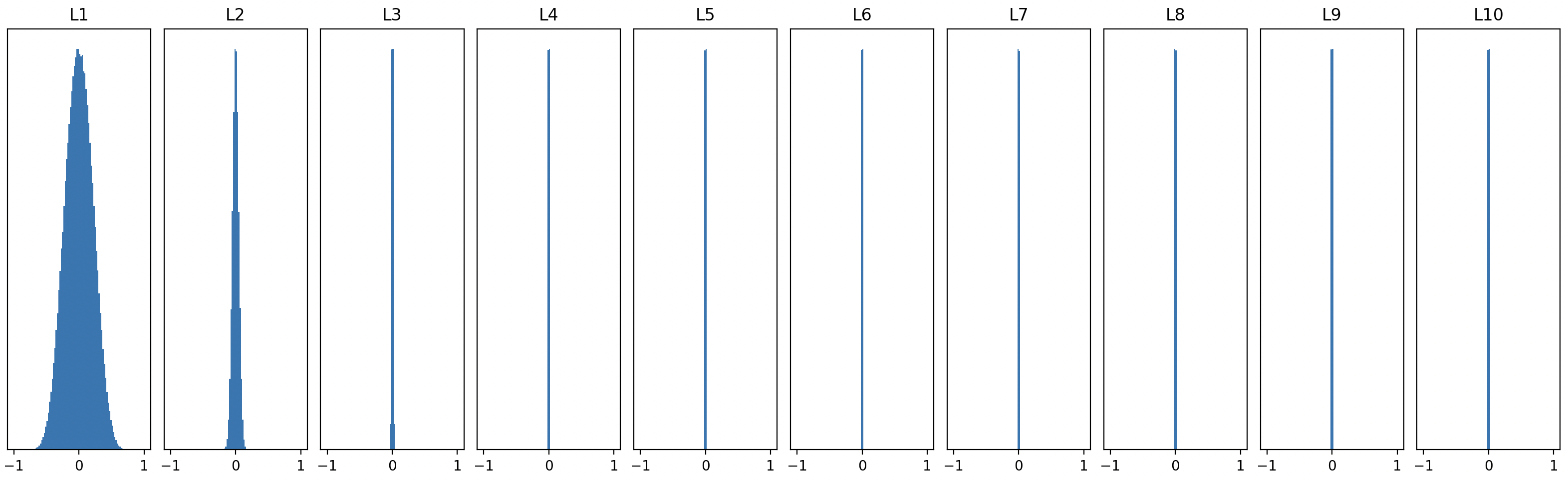
위처럼 표준편차 0.01인 정규분포에서 파라미터를 뽑으면, 대부분의 파라미터의 절댓값이 0.02 이내가 되고, 그런 작은 수들이 레이어를 지날 때마다 계속 곱해집니다. 작은 숫자들의 반복 곱은 각 레이어의 활성값(activation) 분포 분산을 점점 줄입니다. 이게 왜 문제일까요?

\[\frac{\partial L}{\partial W^{[j]}} = \frac{\partial L}{\partial \hat y} \cdot {\frac{\partial \hat y}{\partial z^{[n]}}} \cdot \underbrace{ \frac{\partial z^{[n]}}{\partial a^{[n-1]}} }_{=W^{[n]}\sim\mathcal N(0, 0.01^2)} \cdot {\frac{\partial a^{[n-1]}}{\partial z^{[n-1]}}} \cdot \underbrace{ \frac{\partial z^{[n-1]}}{\partial a^{[n-2]}} }_{=W^{[n]}\sim\mathcal N(0, 0.01^2)} \cdot \space \cdots \space \cdot {\frac{\partial a^{[j+1]}}{\partial z^{[j+1]}}} \cdot \underbrace{ \frac{\partial z^{[j+1]}}{\partial W^{[j]}} }_{\approx 0}\]

문제는 Backpropagation에서 Chain rule에 의해 다음 레이어들의 가중치가 계속 곱해진다는 점에 있습니다. 그 값들이 대체로 0.02 안팎의 작은 수라 전체 기울기가 빠르게 작아집니다. 게다가 식의 끝에는 해당 레이어 입력(이전 레이어의 Activation)이 곱해지는데, 이 값도 레이어를 거듭할수록 작아지죠. 결과적으로 초반 레이어는 이후 레이어의 작은 가중치들이 줄줄이 곱해져 기울기가 작아지고, 후반 레이어는 입력 Activation 자체가 작아서 기울기가 작아지는 상황에 빠집니다.

\[W \sim \mathcal{N}(0, 1) \times 1\]

그러면 초기 분포를 크게 잡으면 나아질까요? 위와 같이 표준정규분포에서 가중치를 뽑으면 각 레이어의 activation 분포가 아래처럼 바뀝니다.

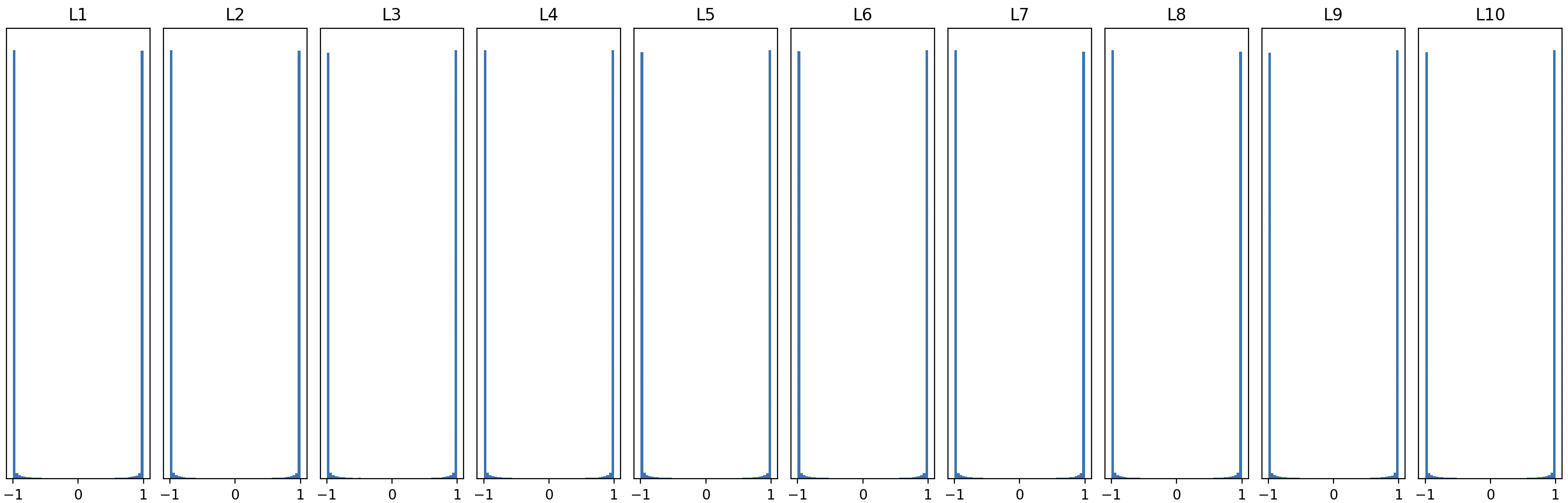
대부분의 값이 -1과 1 근처에 몰리는 모습입니다. 이 경우 어떤 문제가 생길까요?

\[\frac{\partial L}{\partial W^{[j]}} = \frac{\partial L}{\partial \hat y} \cdot {\frac{\partial \hat y}{\partial z^{[n]}}} \cdot \frac{\partial z^{[n]}}{\partial a^{[n-1]}} \cdot \underbrace{ {\frac{\partial a^{[n-1]}}{\partial z^{[n-1]}}} }_{\approx 0} \cdot \frac{\partial z^{[n-1]}}{\partial a^{[n-2]}} \cdot \space \cdots \space \cdot \underbrace{ {\frac{\partial a^{[j+1]}}{\partial z^{[j+1]}}} }_{\approx 0} \cdot \frac{\partial z^{[j+1]}}{\partial W^{[j]}}\]

활성화 함수의 포화 구간(tanh에서 기울기가 평평해지는 구간)으로 입력이 들어가면, 그 구간의 기울기가 거의 0에 가까워집니다. 따라서 해당 항들이 0에 수렴해 전체 기울기가 다시 작아지죠. 즉, 초기 분포를 지나치게 크게 잡아도 기울기 소실이 발생합니다.

\[W \sim \mathcal{N}(0, 1) \times ?\]

그러니까 어떤 표준편차를 가지는 정규분포에서 가중치를 추출할 것인가가 굉장히 중요한 문제라는 것이죠.

Solution

모든 레이어에서 Activation 분포가 적절하게 유지되도록 해주는, 가장 널리 쓰이고 경험적으로 성공적인 방법이 Xavier Initialization입니다.

\[W \sim \mathcal{N}(0, 1) \times \frac{1} { \sqrt { \text{fan in} } }\]

입력 차원(fan in)의 제곱근의 역수를 표준편차로 하는 정규분포에서 가중치를 샘플링합니다. 이렇게 하면 깊은 레이어까지도 아래와 같이 꽤 이상적인 Activation 분포가 유지됩니다.

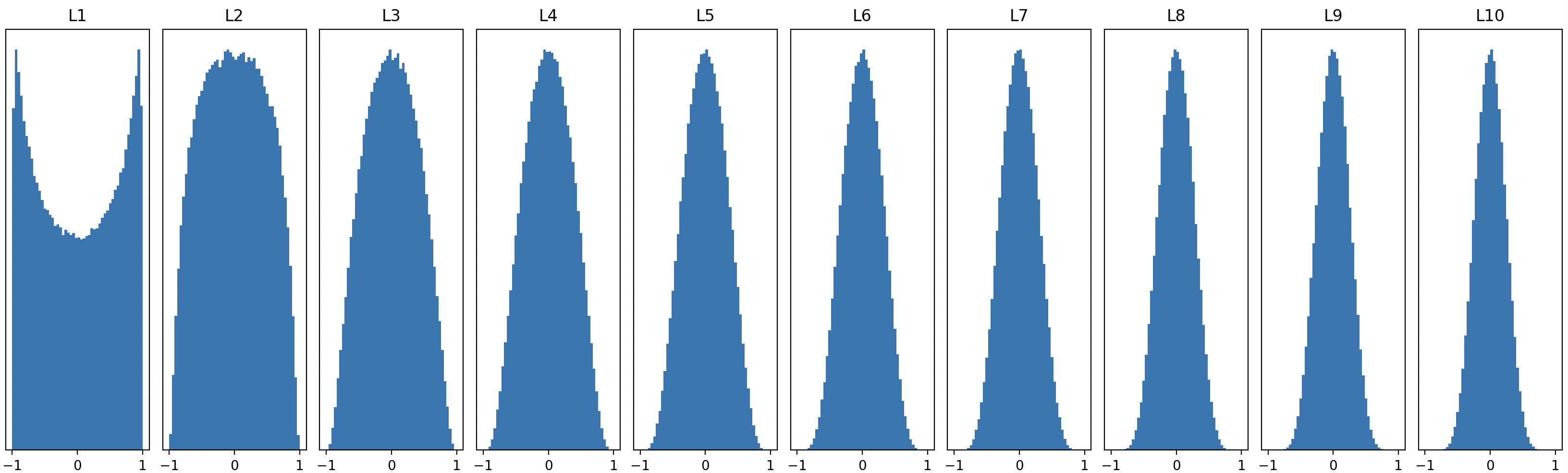
왜 잘 동작할까요? 직관적으로, 입력 차원이 작을 때는 나눠주는 수가 작아 상대적으로 분포가 크게 유지되고, 입력 차원이 클 때는 더 크게 나눠줘 분포를 좁혀 주기 때문입니다.

조금 더 구체적으로 살펴볼 건데, 그 전에..

\[Var(A + B) = Var(A) + Var(B)\] \[Var(AB) = Var(A) \times Var(B)\]

서로 독립인 확률변수의 합의 분산은 각 분산의 합과 같고, 곱의 분산은 각 분산의 곱과 같습니다. 이제 신경망에 이 내용들을 적용해봅시다.

\[W^{[j]}a^{[j-1]} = z^{[j]}\] \[w^{[j]}_1 a^{[j-1]}_1 + w^{[j]}_2 a^{[j-1]}_2 + \cdots + w^{[j]}_\text{fan in} a^{[j-1]}_\text{fan in} = z^{[j]}\]

계산의 편의를 위해서 $b^{[j]}$(bias)항은 제외합니다. 위 가중치와 이전 레이어 Activation의 곱이 만드는 출력의 분산을 구해보면 아래와 같습니다.

\[w^{[j]}_n \sim \mathcal N(0, k), \space \space \space Var(w^{[j]}_n) = k\] \[Var(a^{[j-1]}_n) = p\] \[Var(w^{[j]}_n a^{[j-1]}_n) = kp\] \[Var( w^{[j]}_1 a^{[j-1]}_1 + w^{[j]}_2 a^{[j-1]}_2 + \cdots + w^{[j]}_\text{fan in} a^{[j-1]}_\text{fan in}) = \text{fan in}\space \times kp\] \[Var( z^{[j]}) = \text{fan in}\space \times kp\]

여기서 tanh 활성화 함수를 선형함수로 근사합니다. 활성화 함수는 비선형이어야 하는데..? 싶지만 실제로 tanh 끝단 포화구간은 기울기 소실을 유발하기 때문에 많은 값이 0 근처를 지나는게 바람직합니다. tanh는 중심부에서 기울기 1에 가까워 거의 $y=x$의 선형 함수처럼 동작하기 때문에 분포 전파를 대략적으로 살필 때 선형 근사는 유용하고 유효합니다. tanh를 0 근방에서 $y=x$로 근사하면 활성화 전후의 분산은 아래와 같이 동일하게 유지됩니다.

\[Var( z^{[j]}) = \text{fan in}\space \times kp\] \[Var( a^{[j]}) = \text{fan in}\space \times kp\]

이전 레이어의 Activation의 분산 $p$가 현재 레이어의 Activation에서도 동일하게 유지되려려면 가중치 분산을 어떻게 잡아야 할까요?

\[k = \frac{1}{\text{fan in}}\] \[Var( a^{[j]}) = \text{fan in}\space \times \frac{1}{\text{fan in}}p = p\]

레이어의 입력 차수의 역수를 가중치 분산으로 두면 분산이 유지됩니다. Xavier Initialization 식이 바로 여기서 나옵니다.

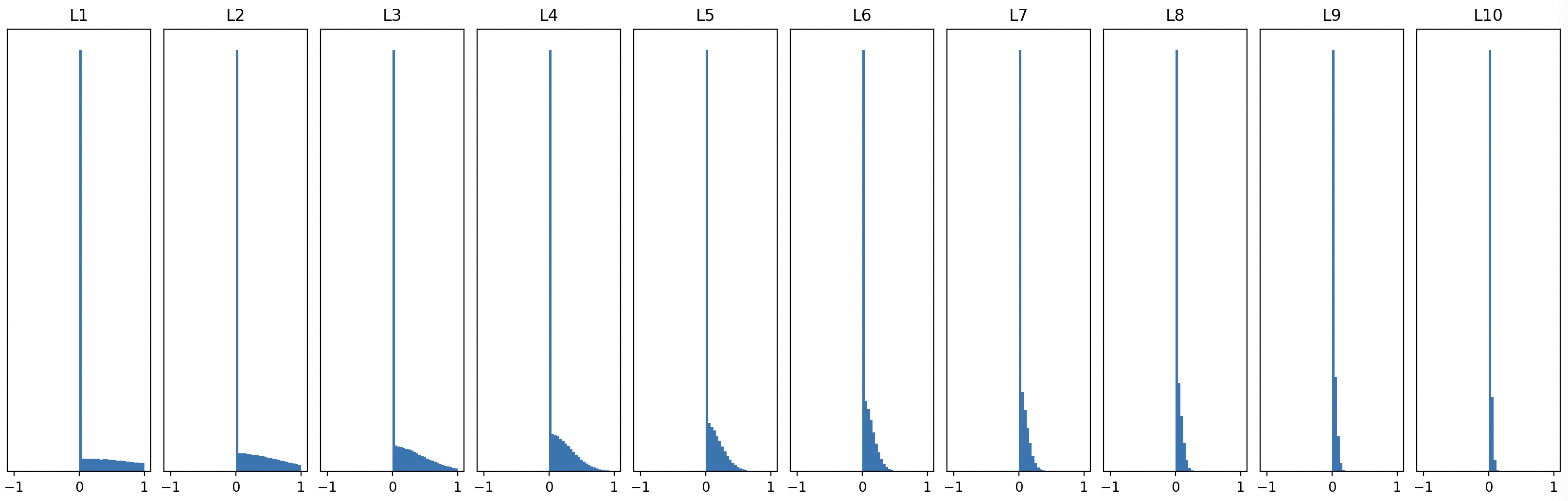
그런데 같은 초기화를 ReLU 네트워크에 그대로 사용하면 위처럼 activation 분포가 조금씩 쪼그라들게 됩니다.

그 이유는 명확한데, 0 근처에서 $y=x$로 근사할 수 있었던 tanh함수와 달리 ReLU는 음수 입력을 절반가량 잘라내는 형태라 출력 분산이 입력 대비 절반으로 줄어듭니다. 그러니까..

\[Var( z^{[j]}) = \text{fan in}\space \times kp\] \[Var( a^{[j]}) = \frac{\text{fan in}\space \times kp}{2}\]

라는 것이죠. 그래서 ReLU를 쓰는 신경망에서는

\[k = \frac{2}{\text {fan in}}\]

처럼 Xavier보다 2배 큰 분산을 갖는 분포에서 가중치를 뽑는 He Initialization을 사용합니다. 이렇게 하면 분포가 잘 유지됩니다.

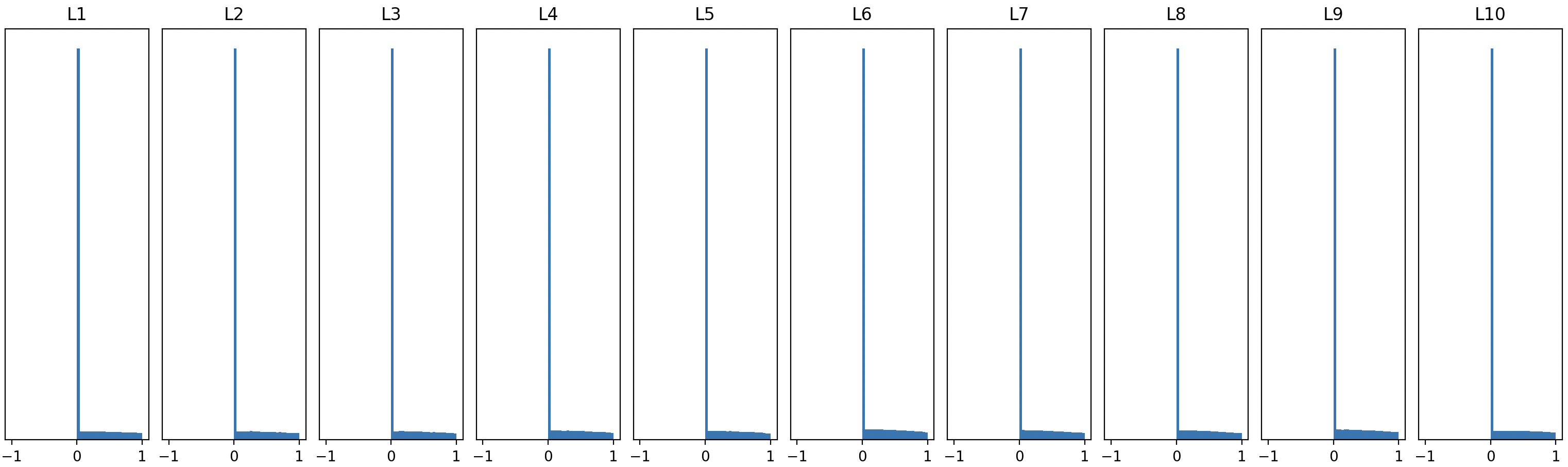
이 포스팅에서 다룬 내용들은 결국 Gradient Vanishing이라는 공통된 문제를 해결해주는 여러 방법들에 관한 것입니다. 다음 포스팅에서는 그 외의 파라미터 최적화 기법과 심층 신경망의 성능을 끌어올리는 여러 테크닉들을 다룹니다.