13 분 소요

이 포스팅은 ‘CS231n의 Lecture 04~05‘에 대한 내용을 담고 있습니다.

자료 출처

Neural Networks

지난 포스팅에 이어 Gradient Descent에 대해 좀 더 다뤄보고, 이어서 선형 분류기보다 더 복잡한 문제를 해결할 수 있는 인공 신경망에 대해서 알아봅니다.

Gradient Descent

Gradient Descent는 손실 함수를 낮출 때 쓰이는 아주 강력한 도구입니다. 쉽게 말해, 우리가 모델 안에 설정할 수 있는 수많은 파라미터(가중치, 편향 등)가 있잖아요? 이 파라미터들을 어떻게 움직이면 분류기의 성능이 좋아질지를 알려주는 것이 바로 Gradient(기울기)입니다.

GD

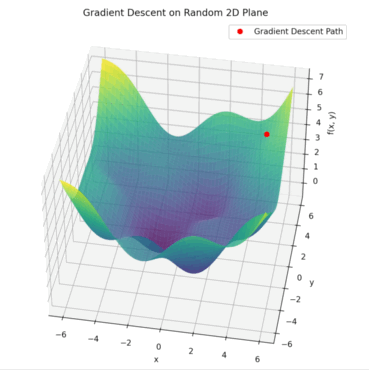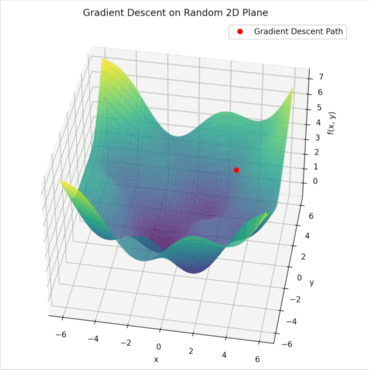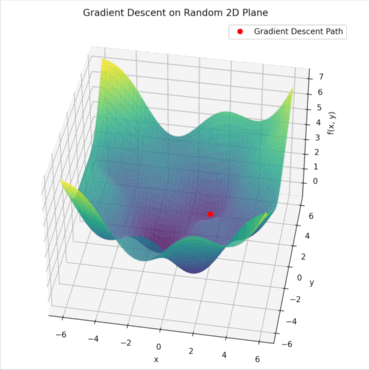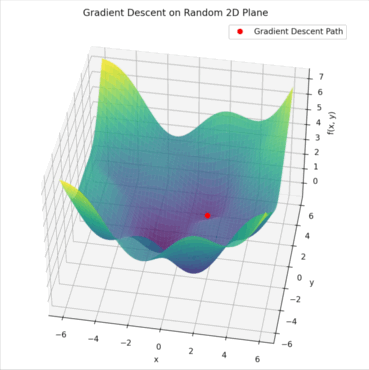
위의 예시를 살펴봅시다. 빨간색 지점이 현재 모델의 파라미터 상태이고, 지도에서의 높이가 손실값이 됩니다. Gradient는 지금 이 방향으로 조금만 움직이면 더 낮은 손실 쪽으로 갈 수 있음을 가리켜주는 화살표 같은 역할을 합니다. 우리는 그 화살표 방향을 따라 조금씩 이동하면서 손실 값을 줄여나가는 거죠. 이 과정이 바로 Gradient Descent입니다.

GDS

\[L(w) = \frac{1}{2}(w-3)^2\]

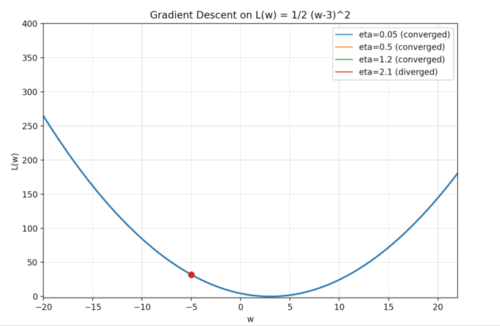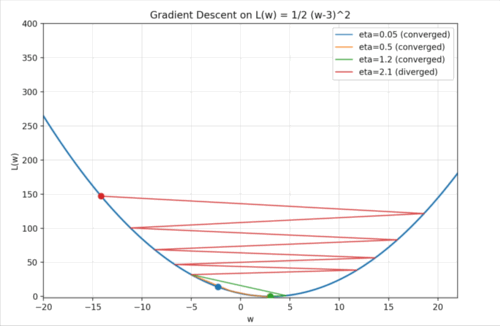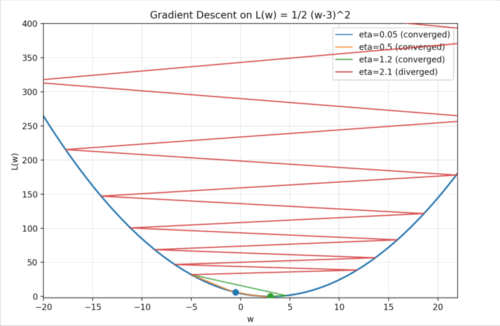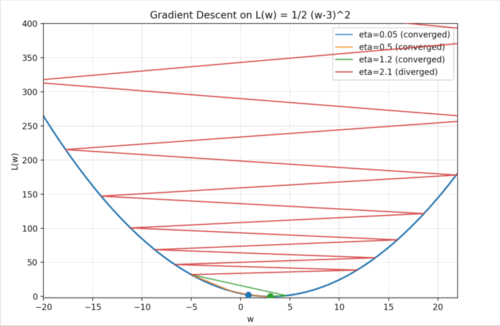
이해를 위해 좀 더 단순한 예시를 만들어 봤습니다. $w$가 -5인 지점에서 출발하는 상황입니다. Gradient Descent는 말 그대로 경사(기울기)를 따라 내려가는 알고리즘이므로, 먼저 기울기를 구하고, 그 기울기의 반대 방향으로 이동하게 됩니다.

그런데 왜 반대 방향일까요? 내리막길이라면 기울기가 음수로 나오고, 오르막길이라면 기울기가 양수로 나옵니다. 만약 기울기가 음수, 내리막길이면 $w$를 양수 방향으로 움직여야 내려가게 됩니다. 반대로 기울기가 양수, 오르막길이면 $w$를 음수 방향으로 움직여야 내려가게 됩니다. 즉, 기울기의 반대 방향으로 이동했을 때 경사를 따라 내려가는 방향으로 변수가 움직입니다.

이 과정을 수식으로 쓰면,

\[w \leftarrow w - \eta \nabla_wL(w)\]

이렇게 표현됩니다.

위 식에서 $\eta$는 한 번 이동할 때의 기본 보폭을 의미하고요, Learning Rate(학습률)이라고 부릅니다. 정리하면 기울기의 크기에 따라(가파르면 많이 움직이고, 완만하면 조금 움직이고), 그리고 정해진 기본 보폭에 곱해져서 최종적으로 움직이게될 거리가 결정됩니다.

이 Learning rate를 어떻게 설정하느냐가 Gradient Descent에서는 굉장히 중요합니다. 예를 들어, $\eta$를 너무 크게 잡으면 어떻게 될까요..? 위 예시의 빨간 점처럼, 내려가는 방향으로 움직였지만 보폭이 너무 커서 극소값을 지나쳐 버리고 오히려 더 높은 지점으로 올라가게 됩니다. 그러면 기울기가 더 커지고, 다시 큰 폭으로 움직여 더 멀리 올라가고… 이런 식으로 값이 점점 발산하게 됩니다. 반대로, $\eta$가 너무 작으면 어떻게 될까요..? 파란 점처럼 아주 천천히 경사를 따라 내려가게 됩니다. 결국 극소값에는 도달하겠지만, 그 과정이 너무 느려져 학습 속도가 비효율적이 됩니다. 위 예시에서 주황색과 초록색 점처럼 적절한 Learning Rate를 선택하면 빠르고 안정적으로 극소값에 도달할 수 있습니다.

남은 문제는 그 화살표, 기울기를 어떻게 구할 것이냐입니다. 기울기를 구하는 방식에 따라 Numerical Gradient와 Analytic Gradient, 두 가지 방식으로 구분됩니다.

\[\frac{df(x)}{dx} = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h}\]

Numerical Gradient는 말 그대로, 실제로 파라미터를 아주 조금 바꿔보고 손실 값이 얼마나 변했는지를 직접 계산해서 기울기를 구하는 방식입니다. 위 수식은 우리가 잘 알고있는 미분의 정의인데 이거를 그대로 적용하는 거죠. 다만, 수학적으로는 $h$를 0에 한없이 가깝게 보내야 정확한 기울기 값이 나오지만, 실제 계산에서는 그렇게 하기가 어렵습니다. 대신 컴퓨터가 다룰 수 있는 적당히 작은 소수값을 $h$로 사용하게 되거든요? 이 과정에서 작지 않은 오차가 발생하게 됩니다. 그래서 Numerical Gradient는 직관적으로 이해하기 쉽다는 장점만 있을 뿐, 정확성 면에서는 한계가 있습니다.

게다가 이 방식은 너무 느리다는 단점도 있어서 Numerical Gradient는 실제 학습에서는 거의 쓰이지 않고, 주로 Analytic Gradient 방식의 기울기 계산이 맞는지 디버깅할 때만 사용됩니다.

Analytic Gradient는 반대로, 각 파라미터에 대해 직접 수식을 세워서 기울기를 구하는 방식입니다. 고등학교 때 함수의 도함수를 직접 구했던 것처럼, 손실 함수를 각 파라미터에 대해 편미분해서 얻는 값입니다. 원리적으로 정확하고 빠르지만, 파라미터가 많으면 이걸 다 어떻게 미분하지..? 싶은 생각이 들 수 있죠. 하지만 다행히도, 우리는 이 계산을 Backpropagation이라는 기법을 사용해 단계적으로, 효율적으로 해낼 수 있습니다. 이 Backpropagation이라는 기법이 어떻게 동작하는지 바로 이어서 다루겠습니다.

간단한 모델에서의 Backpropagation

\[f(x, y, z) = (ax + by) \times cz\]

간단한 예시로 위와 같은 모델을 가정해 봅시다. 여기서 $x$, $y$, $z$는 입력 값이고, $a$, $b$, $c$는 우리가 조정할 수 있는 파라미터입니다. 손실 함수는 단순하게 모델의 예측 값과 정답(Ground Truth) 사이의 차이를 기준으로 하겠습니다.

먼저 파라미터를 임의로 초기화해 봅시다.

\[f(x, y, z) = (2x + 5y) \times 1z\]

자 그리고 훈련 데이터 하나를 예시로 들어볼게요.

\[\text{train example:}((x=1, y=2, z=1), \text{ground truth}=15)\]

이 데이터를 모델에 넣어 계산해 보면,

\[\hat y=(2×1+5×2)×(1×1)=(2+10)×1=12\]

예측 값 $\hat{y}$는 12이고, 실제 정답은 15이므로 오차는 3입니다. Gradient Descent로 파라미터를 업데이트하려면, 다음 세 개의 기울기가 필요합니다.

\[\frac{\partial L}{\partial a}, \frac{\partial L}{\partial b}, \frac{\partial L}{\partial c}\]

이 세 개의 값들을 구하기 위해 Forward Propagation과 Backpropagation 과정을 거치게 됩니다.

Forward Propagation

FP

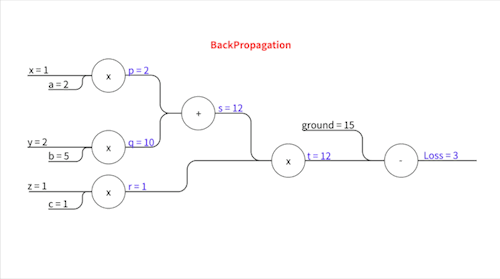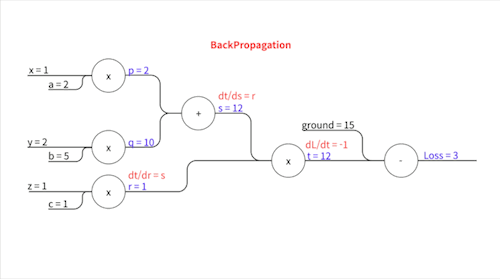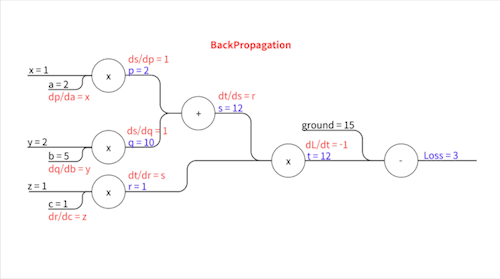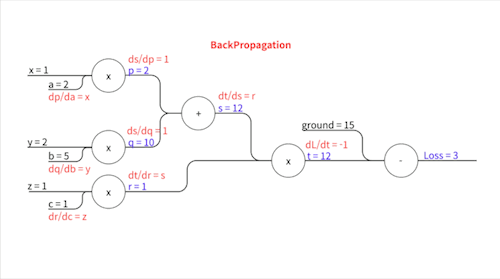
Forward Propagation은 입력에서 시작해 출력(예측 값)까지 차례대로 계산을 진행하는 과정입니다. 다만, 그냥 계산을 해 나가는 것이 아니라 계산 중간 결과들을 위와 같이 모두 저장해둡니다. 이를 Memorization이라고 하는데, 이 중간 값들이 나중에 편미분을 할 때 필요하거든요.. 이 작업이 Forward Propagation의 가장 중요한 부분입니다. 단순히 결과만 구하는 것이 아니라 나중에 실제로 Backpropgation 이라는 편미분(기울기) 값을 계산하는 과정에서 필요한 값들을 기록해 두는 것, 이게 .Forward Propagtion의 핵심입니다.

\[p = a x\] \[q = b y\] \[s = p + q\] \[r = c z\] \[t = s \times r\]

이렇게 중간 변수들을 설정하고요, 실제로 계산을 해보면..

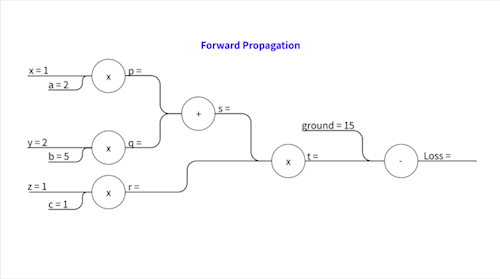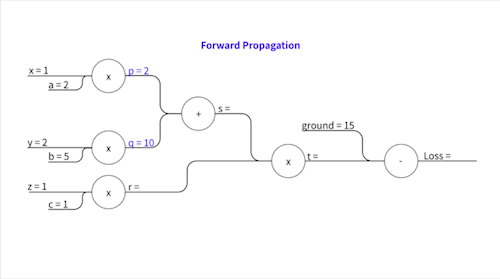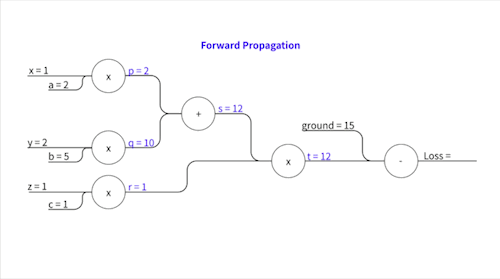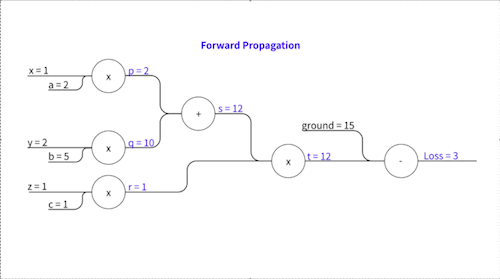
\[p = 2 \times 1 = 2\] \[q = 5 \times 2 = 10\] \[s = 2 + 10 = 12\] \[r = 1 \times 1 = 1\] \[t = 12 \times 1 = 12\]

즉,

\[p=2,\space q=10, \space s=12,\space r=1,\space t=12\]

가 됩니다.

이렇게 저장해 둔 값들을 어떻게 각 파라미터의 변화량에 대한 손실 값의 변화량, 기울기를 계산하는지 Backpropagation 과정을 통해 살펴봅시다.

Backpropagation

Forward Propagation이 끝나면, 이제는 각 파라미터($a$, $b$, $c$)가 손실 값 $L$에 얼마나 영향을 주는지를 말하는 편미분 값, 기울기를 구해야 합니다. 이걸 구해주는 작업이 Backpropagation 입니다. Backpropagation은 손실 값과 각 파라미터 사이의 기울기를 구할 때 Chain Rule을 이용해 계산을 단계별로 전파하는 방법입니다.

Q. Chain Rule이 뭔가요?

Chain Rule은 어떤 값이 여러 단계의 계산을 거쳐서 결정될 때, 각 단계별 변화량을 모두 곱해 전체 변화량을 구하는 방법입니다. 예를 들어, $y = f(u)$이고 $u = g(x)$와 같이 $x$에서 $u$를 거쳐 $y$에 도달하게 되는 식의 흐름을 생각해봅시다. 이 예시에서 $x$에 대한 $y$의 변화량($\frac{dy}{dx}$)은 $\frac{dy}{du}$와 $\frac{du}{dx}$의 곱인 $\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$를 통해 구해집니다. 이 예시보다 더 복잡한 식에서도 위의 예시에서 중간 변수로 $u$를 설정했듯이 더 많은 중간 변수를 통해 여러 간단한 블록으로 쪼갠 다음, 각 구간의 변화율을 곱하면 전체 변화율을 쉽게 구할 수 있습니다. Backpropagation에서는 이 원리를 활용해 손실 값과 식에 존재하는 모든 파라미터 사이의 기울기를 계산합니다.

아 그냥 귀찮게 중간 변수 설정 안 하고 한 번에 각 파라미터에 대해 편미분을 해버리면 되는 거 아닌가?.. 하는 생각이 들죠. 그런데요 그게 사실은 우리가 명시적으로 중간 변수를 쓰지 않을 뿐, 그 과정이 실제로는 중간 변수를 설정해가지고 Chain Rule 경로를 따라 계산하는거랑 동일합니다. 오히려 개별 파라미터에 대해 따로 편미분을 해버리면 Chain Rule 상에 등장하는 동일한 중간 변수에 대한 기울기를 여러 번 계산하는 꼴이 되어버리거든요? 이게 꽤나 큰 비효율을 야기합니다. 때문에 중복 계산을 하지 않도록 Backpropagation이라는 알고리즘을 사용합니다.

BP

아까 위에서 $p = a x$, … 이렇게 여러 중간변수들을 설정했습니다. 그리고 그 각각의 식들은 굉장히 간단한 형태(곱하거나 더하는게 끝)여서 눈으로 바로 계산할 수 있을 정도로 편미분이 쉽습니다. 그걸 다 적어주면요..

\[\frac{\partial L}{\partial t} = -1\] \[\frac{\partial t}{\partial s} = r\] \[\frac{\partial t}{\partial r} = s\] \[\frac{\partial s}{\partial p} = 1\] \[\frac{\partial s}{\partial q} = 1\] \[\frac{\partial p}{\partial a} = x\] \[\frac{\partial q}{\partial b} = y\] \[\frac{\partial r}{\partial c} = z\]

이렇게 표현됩니다.

우변에 등장하는 $r$, $s$,… 이 변수들의 값($p=2,\space q=10, \space s=12,\space r=1,\space t=12$)을 Forward Propagation에서 다 구했었죠? $x$, $y$, $z$는 입력값으로 우리에게 주어진 값($x=1,\space y=2,\space z=1$)입니다. 이 친구들을 대입하면..

DI

\[\frac{\partial L}{\partial t} = -1\] \[\frac{\partial t}{\partial s} = 1\] \[\frac{\partial t}{\partial r} = 12\] \[\frac{\partial s}{\partial p} = 1\] \[\frac{\partial s}{\partial q} = 1\] \[\frac{\partial p}{\partial a} = 1\] \[\frac{\partial q}{\partial b} = 2\] \[\frac{\partial r}{\partial c} = 1\]

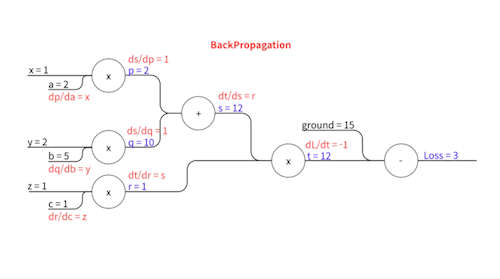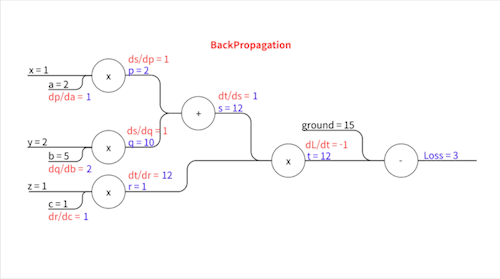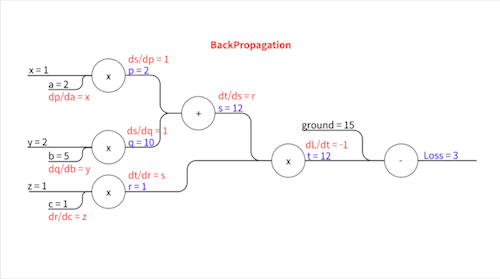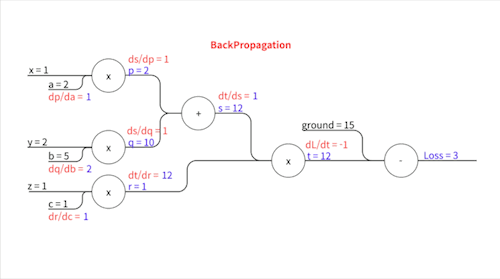
위와 같습니다. 이제 각각의 파라미터에 대한 기울기를 구하기 위해 Chain Rule을 사용합니다.

EE

\[\frac{\partial L}{\partial a} = \frac{\partial L}{\partial t} \cdot \frac{\partial t}{\partial s} \cdot \frac{\partial s}{\partial p} \cdot \frac{\partial p}{\partial a} = (-1) \cdot 1 \cdot 1 \cdot 1 = -1\] \[\frac{\partial L}{\partial b} = \frac{\partial L}{\partial t} \cdot \frac{\partial t}{\partial s} \cdot \frac{\partial s}{\partial q} \cdot \frac{\partial q}{\partial b} = (-1) \cdot 1 \cdot 1 \cdot 2 = -2\] \[\frac{\partial L}{\partial c} = \frac{\partial L}{\partial t} \cdot \frac{\partial t}{\partial r} \cdot \frac{\partial r}{\partial c} = (-1) \cdot 12 \cdot 1 = -12\]

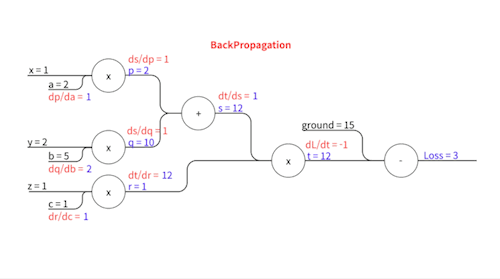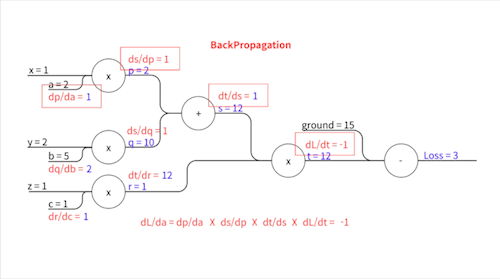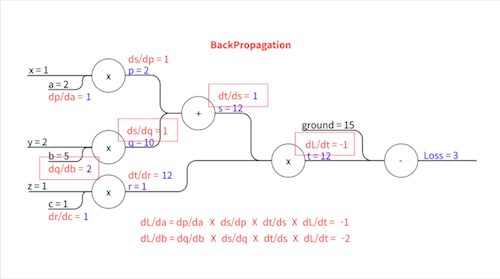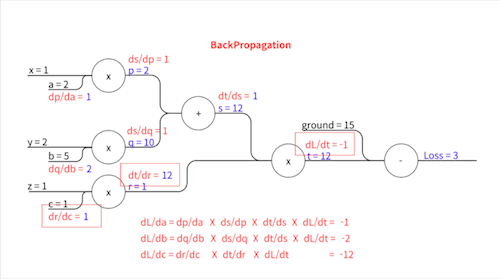
손실 값과 가까운 중간 변수부터 차례차례 기울기가 전파되어 나가는 모습을 볼 수 있죠. 이 과정에서 각 중간 변수에 한 번 씩만 편미분하기 때문에 각 파라미터에 대해 따로따로 편미분을 할 때보다 훨씬 더 효율적입니다.

위에서 다룬 예시는 아주 단순한 형태의 모델이었지만, 우리가 이전 포스팅에서 다뤘던 선형 분류 모델만 해도 훨씬 더 복잡한 구조를 가지고 있었습니다. 거기서는 가중치 행렬과 입력 벡터의 곱, 편향 벡터의 합과 같이 단순 스칼라 곱셈이 아니라 행렬 단위로 연산이 수행됩니다. 그런데요..

\[ax + by = z\] \[cx + dy = w\]

라는 두 식이 있을 때, 이 친구들을..

\[\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} z \\ w \end{pmatrix}\]

이렇게 선형 시스템으로 표현할 수 있었죠? 그 반대도 똑같습니다. 행렬로 표현된 식들도 결국은 각각의 스칼라 식들의 모음일 뿐입니다. 스칼라 식들로 풀어 쓴 다음에 위에서 살펴본 예제와 똑같이 각 항목별로 Backpropagation이 수행하면 됩니다. 그러니까 행렬 형태를 쓴다고 해서 행렬인 경우에는 어떻게 하지?.. 라고 전혀 걱정할 필요가 없다는거죠.

실제 계산에서는 행렬 연산의 장점을 살려 한 번에 편미분을 하거나, 벡터·행렬 형태 그대로 미분 공식을 적용해 효율적으로 구현하지만, 그 계산의 근본 원리는 우리가 지금 본 단순한 스칼라 예제와 동일합니다.

Neural Networks

지금까지 선형 분류 모델 구조, 그리고 해당 모델을 최적화시키기 위한 여러 기법들에 대해서 다루어 봤습니다. 그런데 선형 분류 모델으로는 죽었다 깨어나도 절대 풀지 못하는 문제들이 있습니다. 가장 대표적인 예가 XOR 분류 문제입니다.

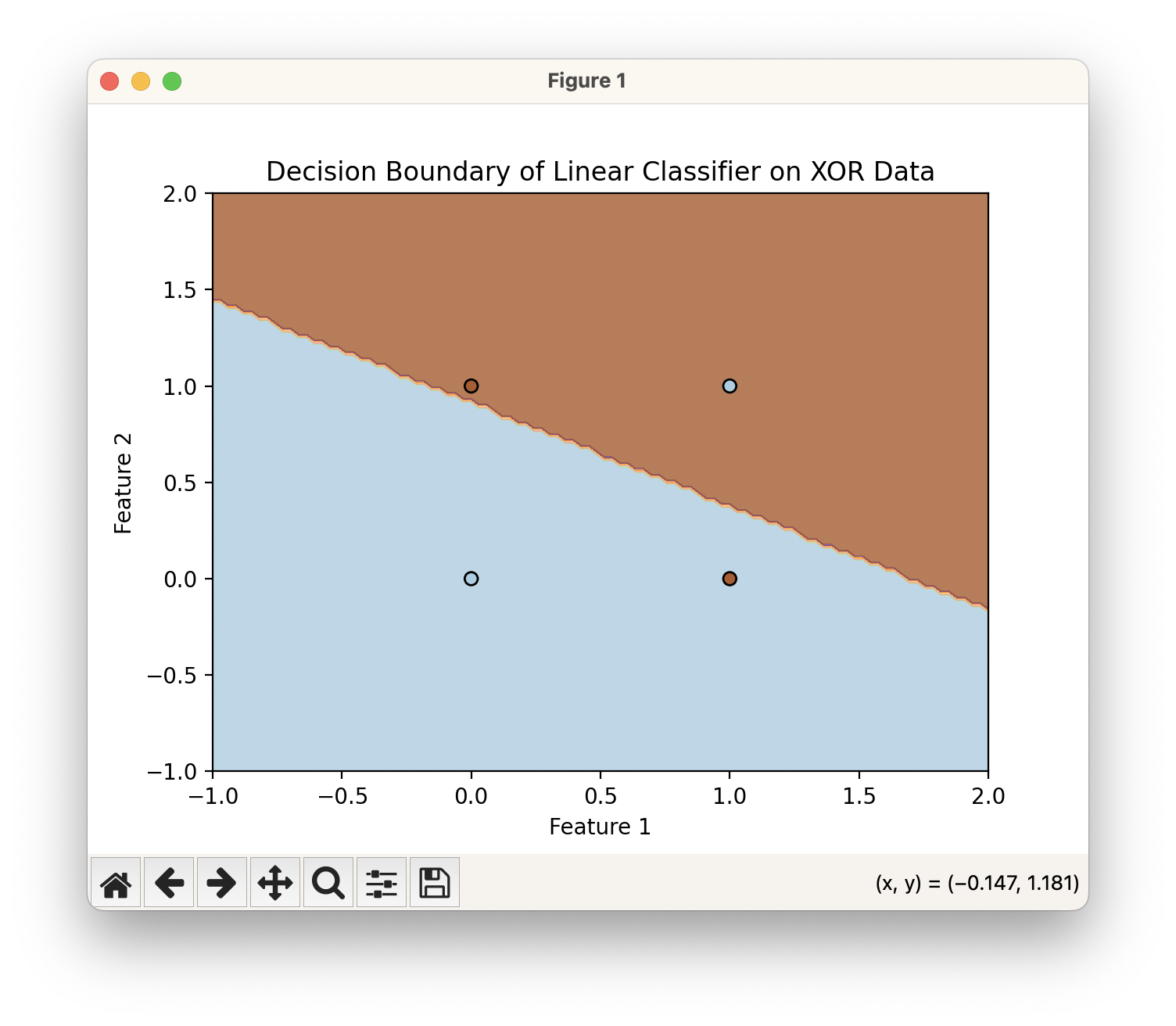
image-20250728230415643

XOR 분류 문제는 말 그대로 XOR로, 서로 교차하는 대각선으로 분포하는 두 집단을 분류하는 문제입니다. 그리고 보시는 바와 같이 하나의 직선 결정 경계로는 두 집단을 결코 나눌 수 없습니다.

그렇다면 선형 레이어를 여러 개 쌓으면 되지 않나..? 하는 생각이 들죠. 레이어를 여러 층으로 쌓으면 파라미터 개수가 늘어나고 모델의 용량이 커져서 더 복잡한 결정 경계를 만들 수 있을 것도 같습니다. 그런데요 실제로는 선형 레이어을 아무리 많이 쌓아도 결국 하나의 선형 계층과 수학적으로 동일합니다.

\[\mathbf{h} = W^{[1]}\,\mathbf{x} + \mathbf{b}^{[1]}\] \[\mathbf{y} = W^{[2]}\,\mathbf{h} + \mathbf{b}^{[2]}\]

위 수식은 $\mathbf h$ 라는 중간 변수를 통해 두 개의 선형 레이어가 이어지는 모델입니다. 두 식을 하나의 식으로 합쳐서 표현해볼게요.

\[\mathbf{y} = \bigl(W^{[2]} W^{[1]}\bigr)\,\mathbf{x} + \bigl(W^{[2]}\mathbf{b}^{[1]} + \mathbf{b}^{[2]}\bigr),\]

이렇게 표현이 되는데요, 이건 결국

\[\mathbf{y}= W\,\mathbf{x} + \mathbf{b}\]

위와 같이 하나의 선형 레이어 꼴로 환원됩니다.

다시 말하면, 아무리 많은 선형 레이어를 쌓아 만든 모델도 하나의 선형 레이어만으로 충분히 표현 가능하는 얘기가 되고, 당연히 모델의 표현력은 전혀 늘지 않습니다. 여전히 결정 경계는 직선의 형태를 가질 것이고요, XOR 분류 문제는 해결할 수 없습니다. 즉, 선형 변환만 여러 번 반복해봤자 아무 소용 없다는 말입니다.

Sigmoid function - Wikipedia

그렇다면 어떻게 해야 할까요? 해결책은 간단한데요, 선형성 사이에 비선형성을 섞어넣어주면 됩니다. 선형 레이어과 선형 레이어 사이에 비선형 함수(Activation Function)를 넣어주면 더 이상 모든 층이 하나의 선형 레이어으로 합쳐지지 않고, 각 층이 서로 다른 비선형 변환을 만들어낼 수 있습니다.

\[\mathbf{z} = W^{[1]}\,\mathbf{x} + \mathbf{b}^{[1]}\] \[\mathbf h = \phi(\mathbf z)\] \[\mathbf{y} = W^{[2]}\,\mathbf{h} + \mathbf{b}^{[2]}\]

위와 같이 Activation Function을 사용해 선형 레이어의 출력을 비선형적으로 휘어주면 여러 계층이 하나의 선형 함수로 더 이상 통합되지 못하고 각 레이어가 서로 치환되지 않는, 고유한 변환을 수행하게 됩니다. 결과적으로는 복잡하게 구부러진 결정 평면을 만들 수 있게 되는 것입니다.

\[\mathbf{z}_1 = W^{[1]}_1\mathbf{x} + \mathbf{b}^{[1]}_1\] \[\mathbf{h}_1 = \phi(\mathbf{z}_1)\]

여기서 Perceptron이라는 개념이 등장합니다. Perceptron은 입력을 받아 선형 결합을 하고, 그 결과를 비선형 함수로 변환하는 최소 단위입니다. 이때 입력은 벡터일 수 있지만, 출력은 하나의 스칼라 값으로 나옵니다. 즉, 하나의 Perceptron은 여러 입력 값을 모두 가중합한 뒤 bias를 더하고, 이를 Activation Function을 통과시켜 하나의 출력 값을 만드는 구조입니다. 선형 레이어는 이렇게 동작하는 Perceptron 여러 개가 병렬로 연결된 형태입니다. 예를 들어, 입력 차원이 4이고 가중치 행렬이 3 by 4라면, 서로 다른 가중치 벡터를 갖는 3개의 Perceptron이 4차원 입력을 받아 각각 하나의 스칼라 출력을 만든 뒤, 이 값들을 모아 3차원 출력 벡터를 구성하는 것과 같습니다.

1

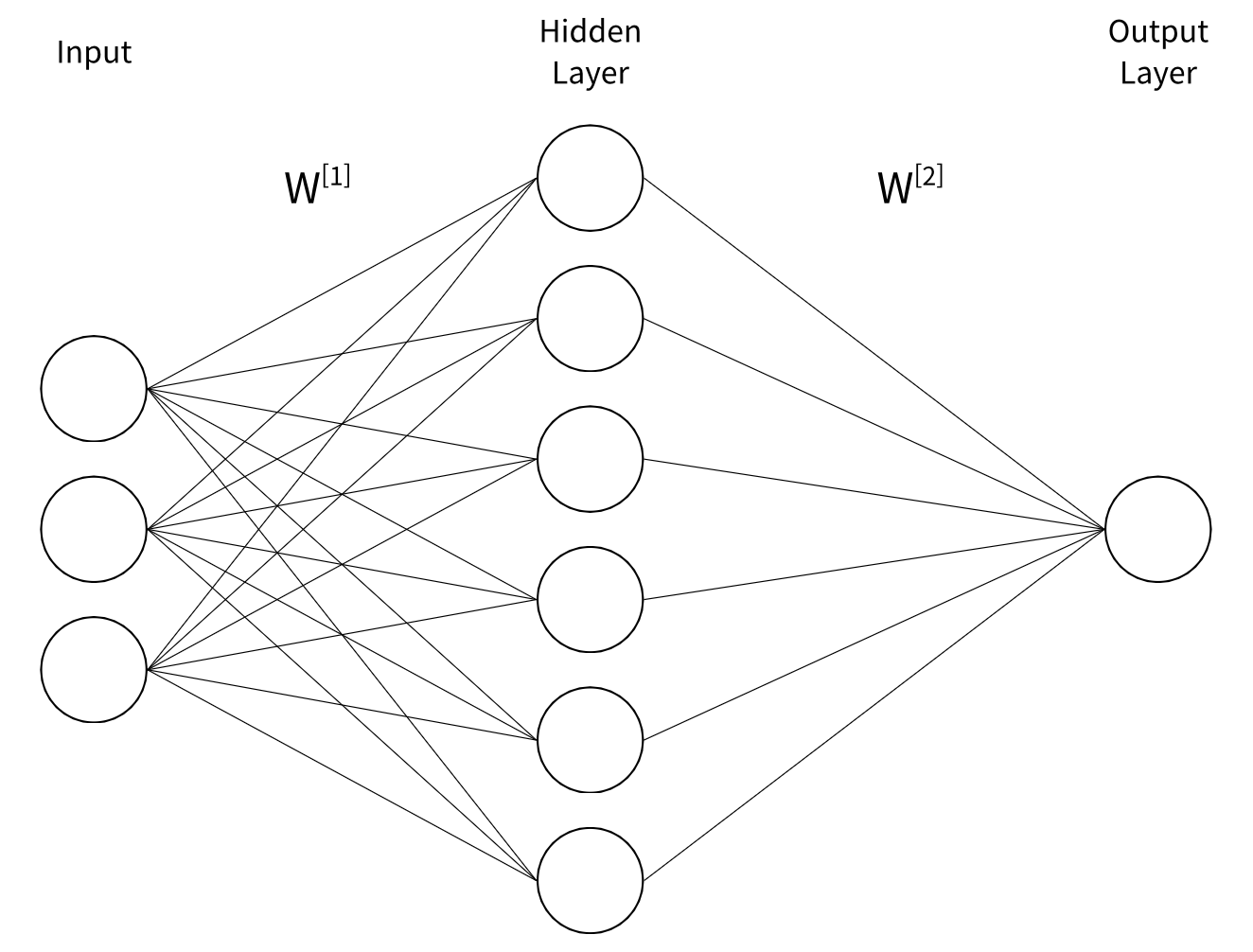
이러한 Perceptron으로 만들어지는 다양한 알고리즘들을 Neural Network(신경망)라고 부릅니다. 특히 여러 층의 Perceptron 레이어를 단순히 차곡차곡 쌓아 올려 구성한 네트워크를 MLP(Multi-Layer Perceptron)라고 합니다. 그림을 보시면 아시겠지만, Perceptron은 이전 레이어의 모든 출력값과 연결되어 있는 구조를 가집니다. 때문에 Perceptron만으로 구성된 선형 레이어를 Fully Connected Layer(완전 연결층)라고도 부릅니다. 각각의 레이어들은 모두 다 자신의 결과값들을 다음 레이어에 전달하게 되는데요, 마지막 레이어가 반환하는 최종 값을 제외한 다른 레이어들의 출력들은 Neural Network 내부에서 은닉된 상태로 존재합니다. 때문에 마지막 최종 레이어를 제외한 중간 단의 레이어들을 Hidden Layer(은닉층)이라고 합니다.

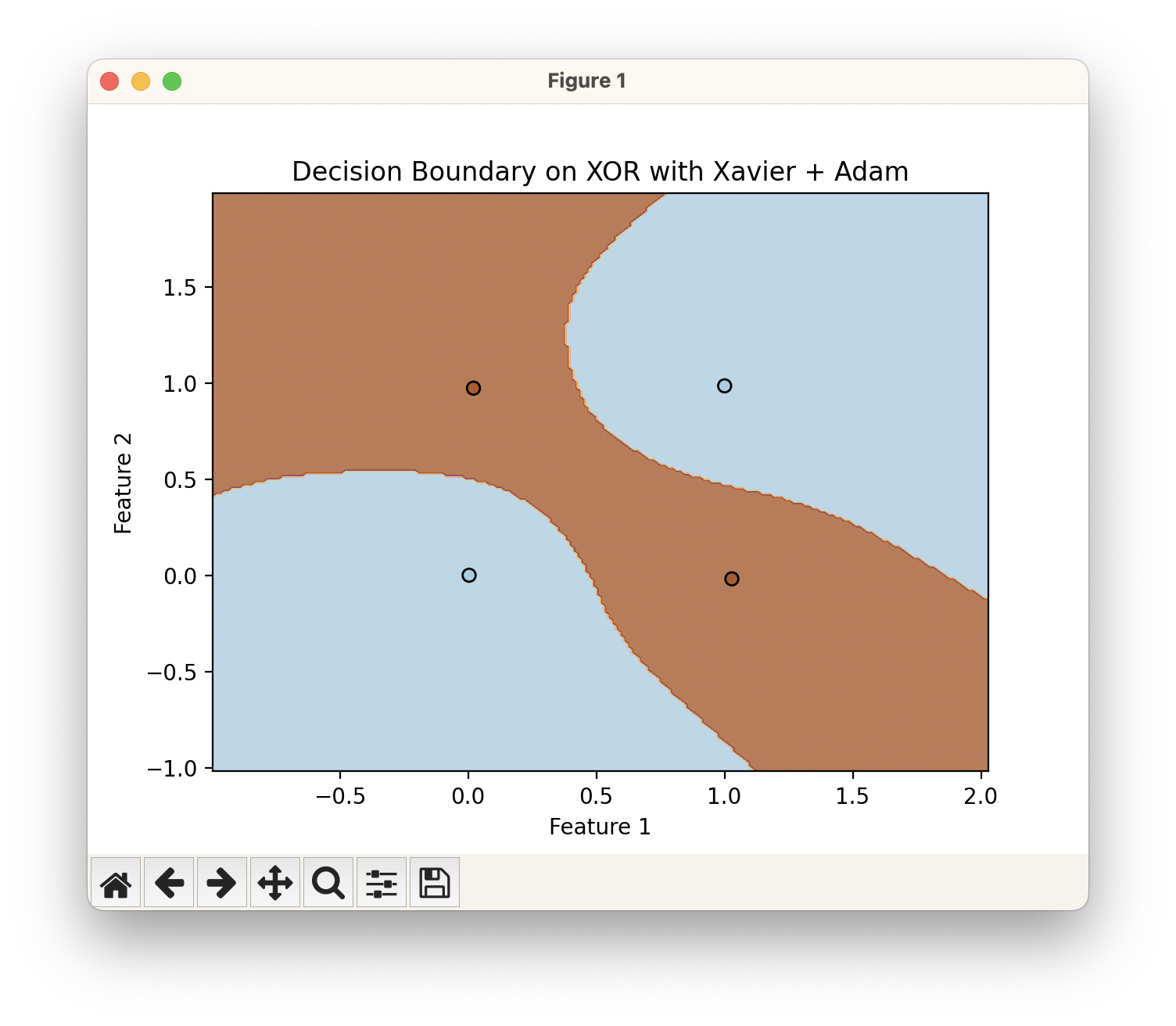
image-20250728234117419

2개층으로 구성한 Neural Network를 사용하니 위와 같이 XOR 분류 문제도 잘 해결되는 것을 확인할 수 있죠. 수학적으로는 단 2개의 층만으로도 세상에 존재하는 모든 분류 문제를 해결할 수 있습니다. 하지만 그걸 위해서는 첫 번째 선형 레이어의 출력 차원이 무한히 커져야 하기 때문에($W^{[1]}$의 모양이 입력차원 by $\infty$), 필요 파라미터의 수가 너무 커지게 됩니다. 또, 실제로 학습을 시켜보면 사용되는 파라미터의 개수 대비 성능도 처참합니다. 때문에 선형 레이어의 크기를 늘려서 모델의 사이즈를 키우는게 아니고요, 선형 레이어를 여러 장 쌓아서 모델의 사이즈를 키우는 방식을 채택하고 그렇게 했을 때 성능이 잘 나옵니다. 그런데 레이어를 여러 장 쌓게되면, 또 그것에 따른 여러 문제점들이 발생하게 됩니다. 그걸 해결하는 방법은 다음 포스팅에서 다루게 됩니다.

Convolution Neural Networks

일반적으로 MLP로 이미지를 분류하려면 일단 2차원 이미지를 일렬로 펴서 하나의 벡터로 만들어야 합니다. Perceptron은 모든 입력값과 연결되기 때문에 시작 정보의 공간 근접성이라는 특징을 무시하죠. 그러니까 굳이 볼 필요 없어 보이는 픽셀들을 함께 묶어 연산도 포함되는데, 이게 연산에 있어 꽤나 많은 부분을 차지해서 특히 고해상도 이미지에서는 크게 비효율적입니다.

CNN(Convolution Neural Networks)는 주변 픽셀끼리들만 보자는 아이디어로 공간적 근접성을 고려할 수 있는 커널이라는 아이디어를 도입해 파라미터의 개수를 획기적으로 줄이면서도 더 높은 성능을 보입니다. CNN의 아이디어가 자체가 공간적 근접성 정보를 활용해 보자는 거라서, 선형 레이어

img

3 by 3의 커널을 이동시키면서 겹치는 부분의 픽셀들을 모두 곱해 하나의 스칼라 값을 반환하는 그림입니다. 파란색 블록이 입력 이미지가 되구요, 그 위에 3 by 3 커널을 딱 겹쳤을 때 자리가 동일한 숫자끼리 각각 9번을 곱한 값들을 다시 모두 더해 결과 값으로 반환합니다. 위와 같이 이미지가 5 by 5인 경우에는 그 작업을 가로 세로 3번씩, 총 9번을 수행하게 돼서 3 by 3 출력 이미지를 얻게 된 겁니다.

cf

cf2

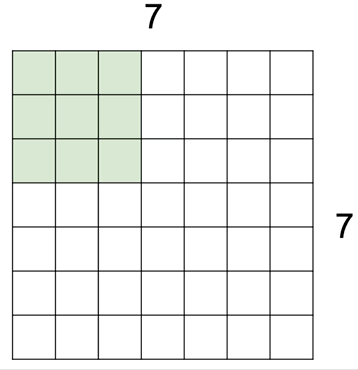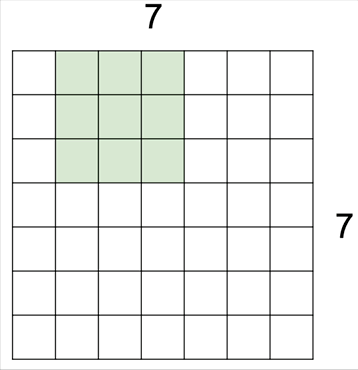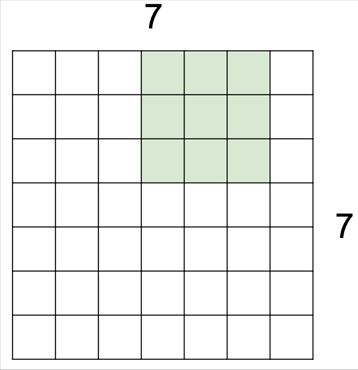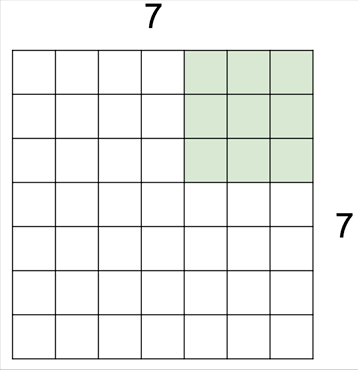
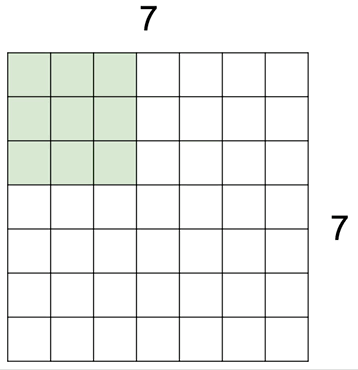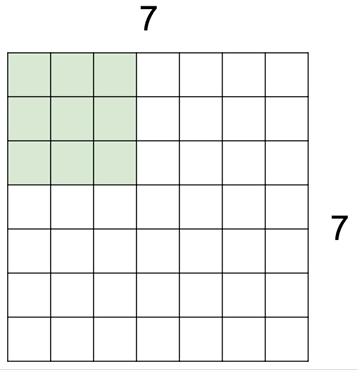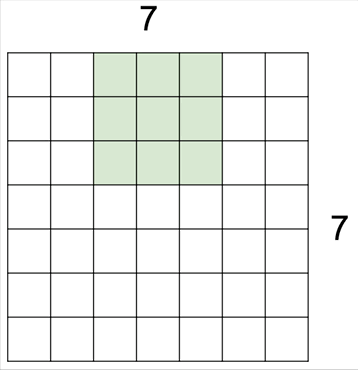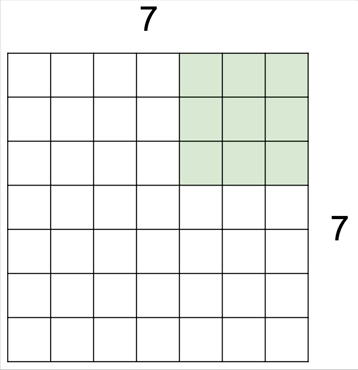
필터를 움직이는 보폭은 반드시 한 칸으로 정해진 것은 아니어서 위와 같이 한발 한발 더 널찍이 이동할 수도 있습니다. 이 경우 출력의 크기가 당연히 더 줄어들게 되겠죠.

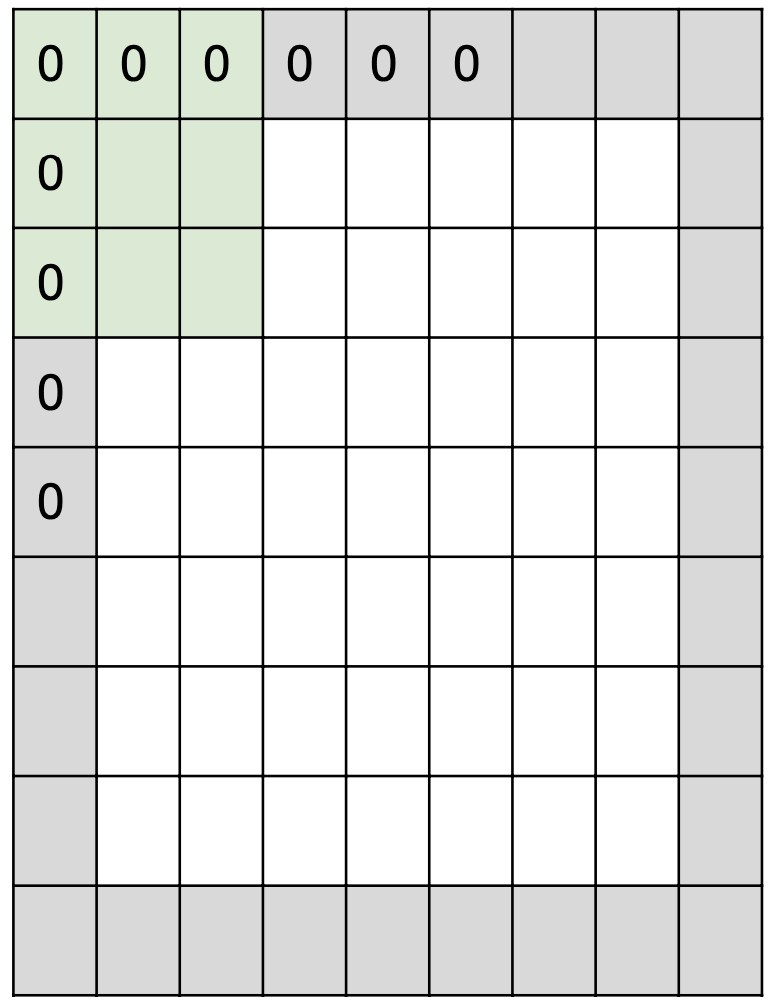
image-20250729101629408

때문에 보통은 가장자리에 0을 덧대어 크기를 유지하거나 혹은 다른 원하는 출력 크기를 얻을 수 있도록 조정해줍니다. 이를 Padding이라고 하고, 특히 위와 같이 0을 덧대는 방식을 Zero-Padding이라고 합니다.

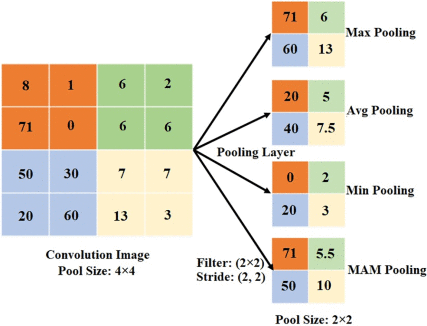
Figure 2

추가로 Pooling이라는게 있는데, 이 친구는 특정 영역 내의 값을 대표값으로 줄여주는 작업을 수행합니다. 가장 일반적인 방법으로는 Max Pooling이 있는데, 작은 윈도우(예: 2×2)를 겹치지 않게 이동시키면서 그 안에서 가장 큰(Max) 값을 선택해 출력합니다. 이것을 레이어 중간중간에 사용해주면 이미지 크기가 줄어들어서 연산량을 줄일 수 있고, 좀 더 이미지의 핵심 추상 정보를 압축시켜주는 효과가 있습니다.

6b81b78c-23ac-4c99-b4a8-fe586ad11ec5_960x540

이미지는 보통 여러 채널을 가지게 되는 경우가 많습니다. 우리가 흔히 보는 이미지들은 다 3개의 RGB 채널로 구성되어 있습니다. 그 경우에는 필터도 입력 이미지와 동일한 차원을 가져야 합니다. 그 결과물로는 가로 세로 길이는 조금 줄어들고 채널은 1인 이미지를 얻게 될 겁니다.

image-20250729102204211

필터 개수당 1차원 출력을 얻게 되고, 필터의 개수만큼 출력 차원이 결정됩니다. 위 경우는 32 by 32 by 3의 이미지에 6개의 5 by 5 by 3 필터를 적용한 예시입니다.

실제로 사용해보자

import os
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms

# 디바이스 설정
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 데이터 전처리
mean = (0.4914, 0.4822, 0.4465)
std  = (0.2023, 0.1994, 0.2010)

transform_train = transforms.Compose([
    transforms.RandomHorizontalFlip(),
    transforms.ToTensor(),
    transforms.Normalize(mean, std),
])

transform_test = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize(mean, std),
])

# 한 번만 다운로드하도록 플래그 설정
download_flag = not os.path.exists('./data/cifar-10-batches-py')

train_dataset = torchvision.datasets.CIFAR10(
    root='./data', train=True, download=download_flag, transform=transform_train)
test_dataset = torchvision.datasets.CIFAR10(
    root='./data', train=False, download=download_flag, transform=transform_test)

train_loader = torch.utils.data.DataLoader(
    train_dataset, batch_size=128, shuffle=True, num_workers=2)
test_loader = torch.utils.data.DataLoader(
    test_dataset, batch_size=100, shuffle=False, num_workers=2)

# 모델 정의
class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        self.conv1 = nn.Conv2d(3, 32, kernel_size=3, padding=1)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
        self.conv3 = nn.Conv2d(64, 128, kernel_size=3, padding=1)
        self.pool = nn.MaxPool2d(2, 2)
        self.fc1 = nn.Linear(128 * 4 * 4, 256)
        self.fc2 = nn.Linear(256, 10)
        self.relu = nn.ReLU(inplace=True)
        self.dropout = nn.Dropout(0.5)

    def forward(self, x):
        x = self.relu(self.conv1(x))
        x = self.pool(x)
        x = self.relu(self.conv2(x))
        x = self.pool(x)
        x = self.relu(self.conv3(x))
        x = self.pool(x)
        x = x.view(-1, 128 * 4 * 4)
        x = self.dropout(self.relu(self.fc1(x)))
        x = self.fc2(x)
        return x

model = SimpleCNN().to(device)

# 손실 함수 & 옵티마이저
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 학습 함수
def train(epoch):
    model.train()
    running_loss = 0.0
    for batch_idx, (inputs, targets) in enumerate(train_loader):
        inputs, targets = inputs.to(device), targets.to(device)
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, targets)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if (batch_idx + 1) % 100 == 0:
            print(f'Epoch {epoch}, Step {batch_idx+1}, Loss: {running_loss/100:.4f}')
            running_loss = 0.0

# 평가 함수
def test():
    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for inputs, targets in test_loader:
            inputs, targets = inputs.to(device), targets.to(device)
            outputs = model(inputs)
            _, predicted = outputs.max(1)
            total += targets.size(0)
            correct += predicted.eq(targets).sum().item()
    print(f'Test Accuracy: {100.*correct/total:.2f}%')

# 메인
if __name__ == '__main__':
    num_epochs = 10
    for epoch in range(1, num_epochs+1):
        train(epoch)
        test()

위 코드는 CNN 레이어를 3층 쌓고, 뒤로 FC 레이어를 2층 쌓아 만든 모델입니다. 보통 CNN을 사용해서 Neural Network를 구성할 때에는 CNN을 앞단에 여러 층 배치한 다음, 뒤에 FC 레이어를 사용해 레이블 개수만큼 원소를 가지는 벡터로 반환하도록 만듭니다. 앞의 CNN 레이어들은 이미지에서 특징들을 뽑아 추상화시키는 역할을 한다고 해서 Feature Extractor(특징 추출기)라고 하구요, 뒤의 MLP 레이어들은 추상화시킨 정보를 바탕으로 분류 작업을 수행하는 역할을 한다고 해서 Classifier(분류기)라고 합니다.

총 10개의 레이블로 구성된 이미지를 분류해야하는 태스크를 학습시켜봤는데요, 약 78%정도의 성능을 확인 가능합니다. MLP로만 구성되는 모델을 동일한 파라미터 수를 가지도록 만들어 학습시켜보면 훨씬 더 낮은 성능이 나오는데, 확실히 공간적 근접성 정보를 잘 활용하는 CNN 아키텍쳐가 이미지를 분류할 때 아주 유리하다는 것을 알 수 있죠.

댓글남기기

참고

Isaac Sim & ROS2

3 분 소요

이 포스팅은 ‘Isaac Lab‘에 대한 내용을 담고 있습니다.