16 분 소요

이 포스팅은 ‘CS231n의 Lecture 01~03‘에 대한 내용을 담고 있습니다.

자료 출처

Computer Vision

먼저 이 강의 전반에서 다루는 주제인 Computer Vision이 무엇인지 살펴봅니다. 이후 Image Classification의 전통적인 방법론들, 그리고 손실 함수와 최적화에 대해 알아봅시다.

Introduction

시각 정보는 생명체가 수집하는 정보들 중 가장 큰 부분을 차지합니다. 이러한 시각 정보들을 담아내기 위한 Camera Obscura와 렌즈 등 다양한 발명품들이 있었고, 이렇게 수집한 수많은 이미지들을 인터넷에서 확인할 수 있습니다.

이런 시각 정보를 컴퓨터에게 ‘이해’시키는 것은 지난 반세기 동안 정말 해결하기 어렵고 난해한 분야였습니다. 하지만 지금에 이르러서는 인간보다도 높은 정확도를 보이기도 합니다. 그만큼 정말 빠른 속도로 발전한 분야이고, 그동안 정말 많은 접근 방법들과 시행착오 끝에 현재는 머신러닝을 기반으로 한 Image Classificaiton이 가장 주를 이루고 있습니다.

Image Classification Pipeline

cat

인간이라면 위 사진을 보고 바로 고양이라고 대답할 수 있습니다(고양이를 본 적이 있는 사람이라면). 인간이 어떠한 물체의 사진을 보고 카테고리를 분류하는 데에는 분명히 어떠한 공통된 방법이 존재할 텐데요, 그게 뭔지 정확하게 기술하는 것은 거의 불가능한 일입니다. 과거 행해졌던 방법 중 물체의 모서리와 코너를 감지하고 ‘고양이 카테고리에 해당하는 사진들의 모서리, 코너들은 이러이러한 분포를 가질거야’라는 식의 특정 카테고리마다 모서리와 코너의 분포 양상을 기술해보려는 시도가 있었습니다. 당시 꽤나 강력한 지지를 받고 많은 연구가 있었지만, 결론적으로는 택도 없는 방법이라는 사실만을 알게되었습니다.

image-20250721000511866

물체의 카테고리를 구별해내는 것은 컴퓨터에게 있어 생각 이상으로 어려운 일입니다. 하나의 카테고리에 해당되는 객체들이 정말 다양하게 존재한다는 점 때문인데요.. 위와 같이 조명 조건에 따라서도..

image-20250721000525591

물체의 자세에 따라서도..

image-20250721000542297

물체를 가리고 있는 배경에 따라서도..

image-20250721000604558

그리고 같은 고양이라고 해도 세부 품종에 따라 이미지에 정말 다양한 픽셀값으로 나타나게 됩니다. 이 수많은 사진들 중 고양이 카테고리만이 가지는 공통된 특징을 통해 고양이 사진을 분류할 수 있는 알고리즘을 적어내는 것은 거의 불가능한 일입니다(애초에 이거다 할 수 있는 명확한 특징이 있기는 한 건지가 의문입니다). 이러한 문제점을 배경에 두고, 카테고리마다 특징을 찾아낼 필요 없이 모든 카테고리들에 대해 공통적으로 적용할 수 있는 ‘데이터 기반 접근 방식(Date-Driven Approach)’이 새롭게 등장하게 됩니다.

Data-Driven Approach

가장 대표적인 데이터 기반 접근 방식으로는 K-Nearest Neighbors(KNN)이 있습니다.

K-Nearset Neighbors

import numpy as np
from sklearn.datasets import make_blobs
from collections import Counter

import matplotlib.pyplot as plt

# Generate a 2D dataset
np.random.seed(42)
X, y = make_blobs(n_samples=90, centers=3, n_features=2, random_state=42)

# Adjust feature values' range to ensure the minimum value is 1.0
X_min = X.min(axis=0)
X += (1.0 - X_min)

# Plot the dataset
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=50)
plt.title("Generated 2D Dataset")
plt.xlabel('leaf length')
plt.ylabel('leaf width')
plt.show()

# k-NN algorithm
def knn_classify(X_train, y_train, X_test, k):
    predictions = []
    for i, test_point in enumerate(X_test):
        # Compute distances from the test point to all training points
        distances = np.linalg.norm(X_train - test_point, axis=1)
        
        # Get the indices of the k nearest neighbors
        k_indices = np.argsort(distances)[:k]
        
        # Get the labels of the k nearest neighbors
        k_labels = y_train[k_indices]
        
        # Determine the most common label
        most_common = Counter(k_labels).most_common(1)[0][0]
        predictions.append(most_common)
        
        # Visualization of progress
        plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap='viridis', s=50, alpha=0.5)
        plt.scatter(test_point[0], test_point[1], c='red', s=100, label='Test Point')
        plt.scatter(X_train[k_indices, 0], X_train[k_indices, 1], edgecolor='black', facecolor='none', s=200, label='Neighbors')
        plt.title(f"Iteration {i+1}: Classifying Test Point")
        plt.legend()
        plt.xlabel('leaf length')
        plt.ylabel('leaf width')
        plt.show()
        
    return np.array(predictions)

# Split the dataset into training and test sets
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]

# Run k-NN with k=5
k = 5
y_pred = knn_classify(X_train, y_train, X_test, k)

# Print the predictions
print("Predicted labels:", y_pred)
print("True labels:", y_test)

KNN 알고리즘은 굉장히 간단하고도 직관적입니다. KNN 알고리즘을 통해 분류를 하기 위해서는 일단은 학습 데이터가 필요합니다. 그리고 이 학습 데이터를 통해 우리가 구분하고자 하는 미관찰 데이터를 분류하게 되는데요, 그 과정은 아래와 같습니다.

예시로 우리가 식물의 종류를 분류해야하는 상황을 가정해봅니다. 단, 여기서 우리가 사용할 수 있는 단서는 잎의 길이와 넓이, 이 두가지 특징 뿐입니다. 총 세 개의 식물 종이 있고, 각 식물 종마다 서른 개의 학습 데이터가 주어집니다(학습 데이터라는 용어가 사용되기는 하지만, 우리가 직관적으로 생각하는 학습이라는 행위가 이 알고리즘에서 수행되진 않습니다. 머신러닝, 인공지능 분야에서는 실제 테스트에 앞서 알고리즘이 필요로하는 데이터를 나이브하게 학습 데이터라고 부르는 관습이 있습니다). 우리가 가진 90개의 모든 학습 데이터를 좌표평면에 찍어보겠습니다.

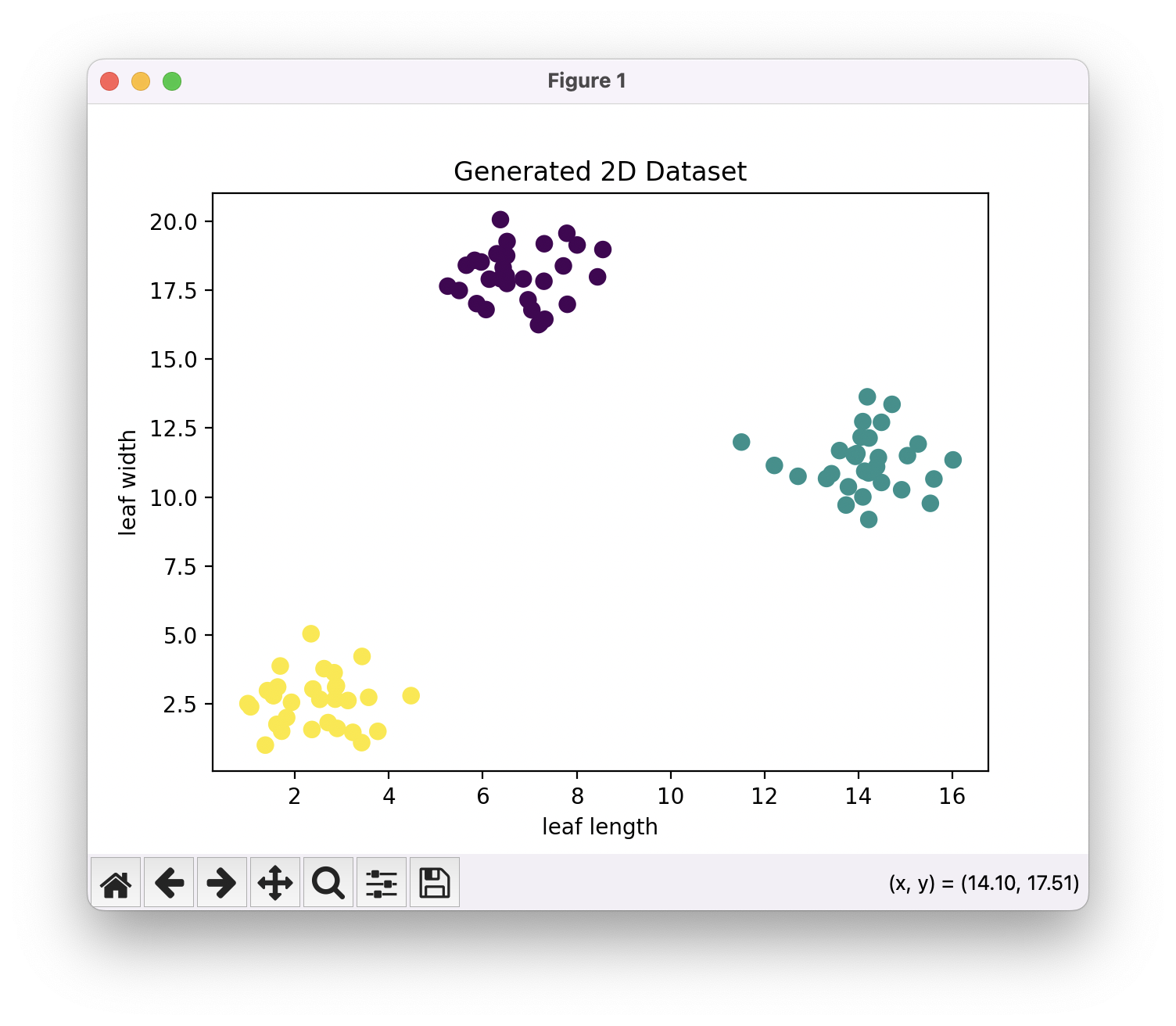
image-20250721012153695

같은 종의 식물들 끼리는 비슷한 잎의 형상을 가질 것입니다. 따라서 학습 데이터들을 찍어보면 같은 종에 속하는 객체들끼리 군집을 이루게 될 가능성이 높습니다.

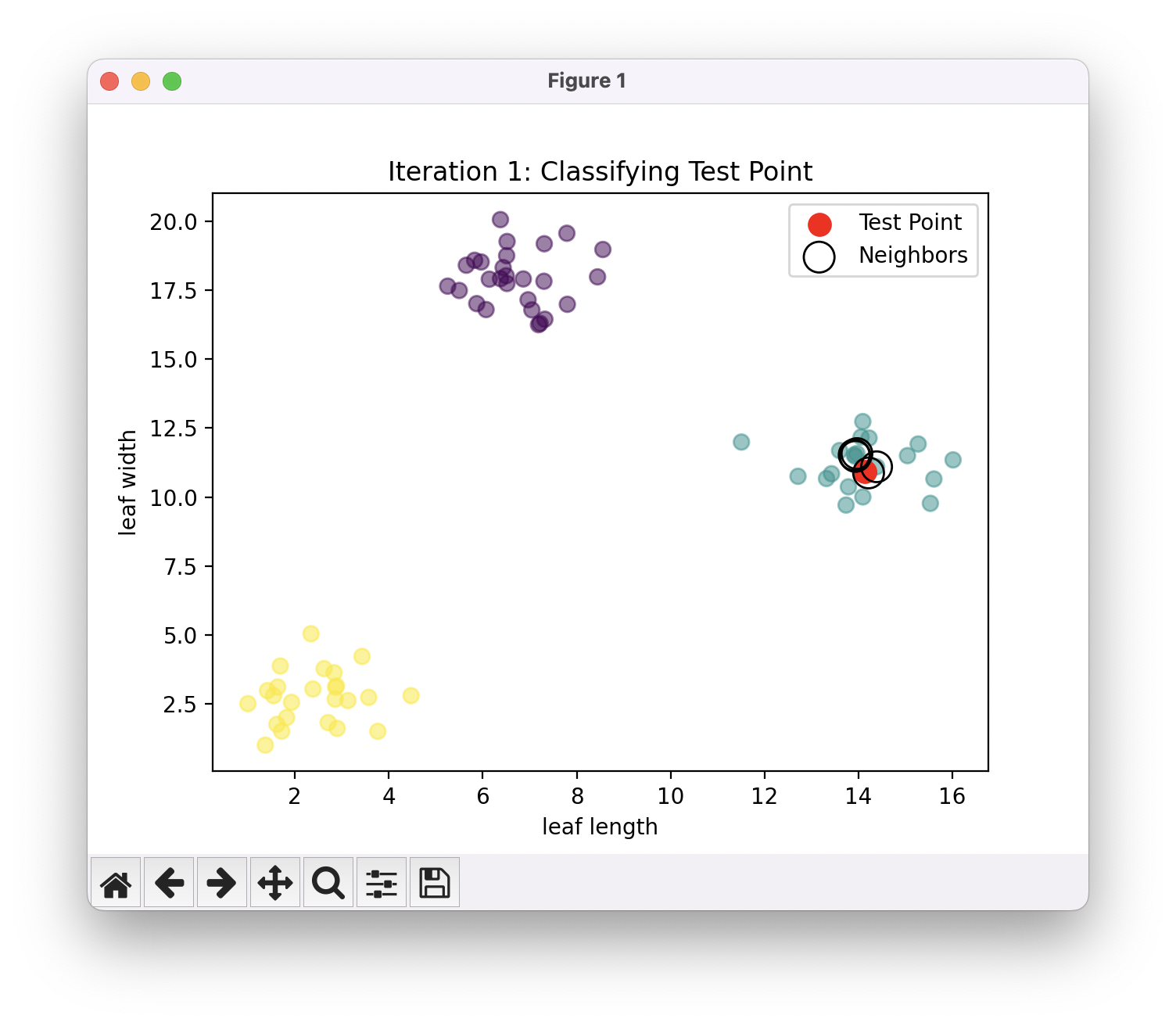
image-20250721012239568

다음으로 우리가 실제로 구분하고자 하는 테스트 데이터를 좌표평면 상에 찍습니다. 그리고 그 점과 가장 가까운 K개의 이웃하는 학습 데이터들의 카테고리를 확인합니다. K값을 5라고 해보면요, 위의 그림에서는 테스트 데이터가 초록색 카테고리의 한 가운데에 위치하고 이 경우 이웃하는 5개의 학습 데이터의 카테고리는 모두 ‘초록색‘입니다. 따라서 테스트 데이터의 카테고리를 ‘초록색‘으로 결정합니다. 이것이 KNN 알고리즘의 수행 과정의 전부입니다.

위 경우에서는 이웃하는 5개의 학습 데이터가 모두 초록색이었습니다. 하지만 세 군집 그 가운데 애매한 곳에 테스트 데이터가 존재할 수도 있겠죠? 그런 경우에는 가장 가까운 5개 이웃의 카테고리가 모두 같지는 않을 수도 있는데, 이 때는 다수결을 통해 가장 많은 이웃이 속한 카테고리로 분류합니다.

용어를 하나 소개하자면 인공지능, 머신러닝 분야에서는 카테고리를 레이블(Label)이라고 부릅니다. 예시로 튤립 레이블, 나팔꽃 레이블, 장미 레이블.. 이런식으로 부릅니다. 이후 문서에서는 카테고리라는 일반적인 용어 대신 레이블이라고 표현하겠습니다.

import numpy as np
from sklearn.datasets import make_blobs
from collections import Counter

import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# Generate a 2D dataset with more overlap between clusters
np.random.seed(42)
X, y = make_blobs(n_samples=90, centers=3, n_features=2, cluster_std=5.0, random_state=42)

# Adjust feature values' range to ensure the minimum value is 1.0
X_min = X.min(axis=0)
X += (1.0 - X_min)

# Plot the dataset
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=50)
plt.title("Generated 2D Dataset")
plt.xlabel('leaf length')
plt.ylabel('leaf width')
plt.show()

# k-NN algorithm
def knn_classify(X_train, y_train, X_test, k):
    predictions = []
    for i, test_point in enumerate(X_test):
        # Compute distances from the test point to all training points
        distances = np.linalg.norm(X_train - test_point, axis=1)
        
        # Get the indices of the k nearest neighbors
        k_indices = np.argsort(distances)[:k]
        
        # Get the labels of the k nearest neighbors
        k_labels = y_train[k_indices]
        
        # Determine the most common label
        most_common = Counter(k_labels).most_common(1)[0][0]
        predictions.append(most_common)
        
    return np.array(predictions)

# Function to plot decision boundaries for all points at once
def plot_decision_boundary(X, y, k):
    h = 0.1  # Step size in the mesh
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    
    # Predict labels for each point in the mesh
    Z = knn_classify(X, y, np.c_[xx.ravel(), yy.ravel()], k)
    Z = Z.reshape(xx.shape)
    
    # Plot the decision boundary
    plt.figure()
    plt.contourf(xx, yy, Z, alpha=0.3, cmap=ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']))
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k', s=50)
    plt.title(f"Decision Boundary (k={k})")
    plt.xlabel('leaf length')
    plt.ylabel('leaf width')
    plt.show()

# Split the dataset into training and test sets
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]

# Run k-NN with k=5
k = 5
y_pred = knn_classify(X_train, y_train, X_test, k)

# Print the predictions
print("Predicted labels:", y_pred)
print("True labels:", y_test)

# Visualize decision boundaries for different values of k
k_values = [1, 3, 5, 7, 9, 11, 13]
for k in k_values:
    plot_decision_boundary(X_train, y_train, k)

K의 값을 5라고 설정할 수도, 7이라고 설정할 수도, 혹은 그 외의 다른 어떠한 숫자로 결정해도 괜찮습니다. 다만 이 값을 홀수로 설정하는 관습이 존재합니다(레이블 개수가 2개일 때 동률이 발생하지 않도록 하기 위해 이 K값을 홀수로 설정하지만, 사실 레이블 개수가 3개 이상부터 큰 의미는 없습니다). 당연히 K값에 따라서 테스트 데이터의 분류 레이블이 바뀔 수 있습니다(3개일 때 [초, 초, 빨] 이었는데, 5개일 때 [초, 초, 빨, 빨, 빨]일 수 있다는 거죠). 위 코드를 실행시켜보시면은 K 값에 따른 분류 레이블의 경계가 어떻게 변화하는지 눈으로 확인할 수 있습니다. 아래는 실행 결과입니다.

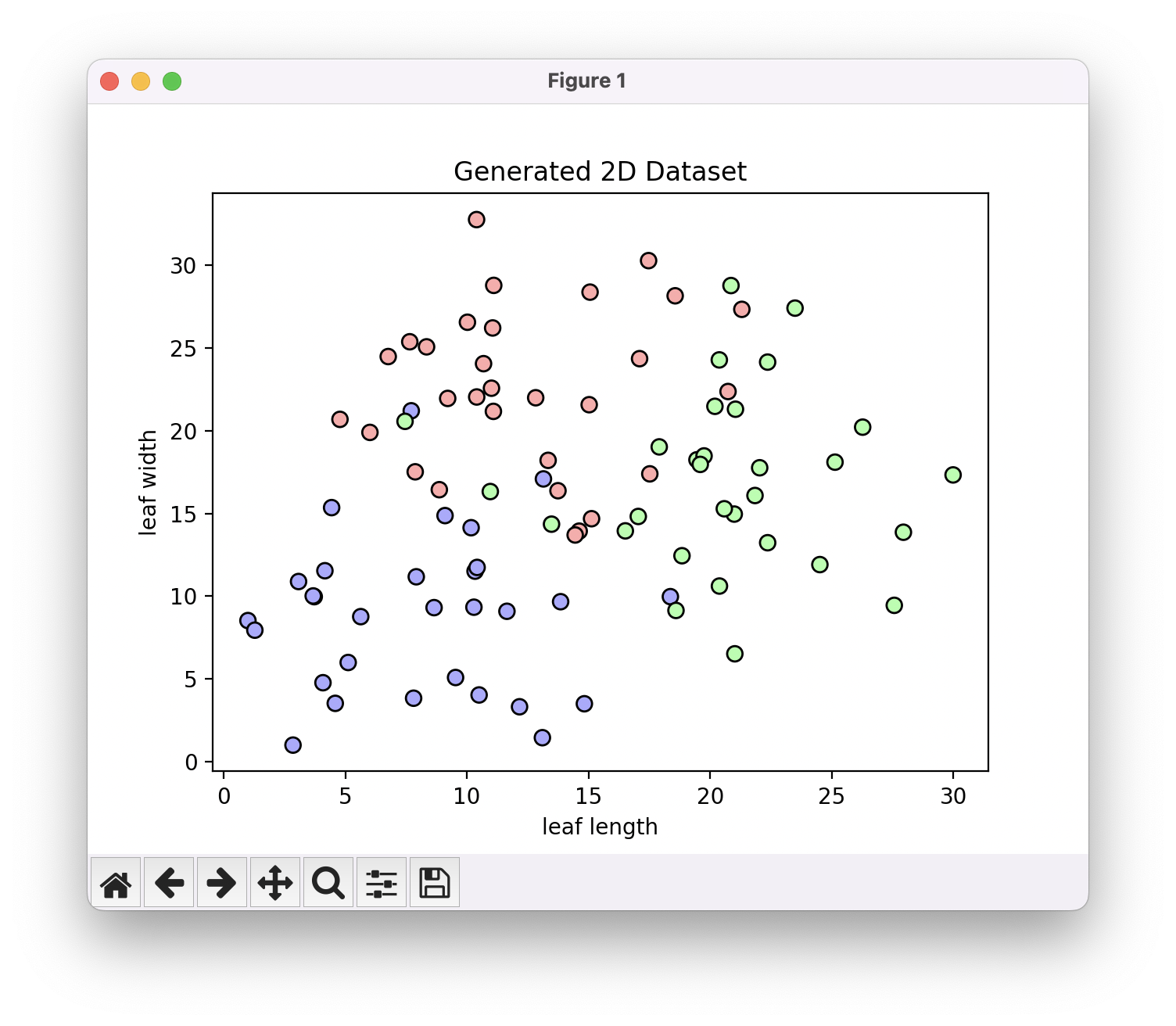
image-20250721020323103

3개의 레이블로 구성된 학습 데이터들이 조금 겹치게 분포한 모습입니다. 당연히 이렇게 겹치게 분포할 수 있는거구요, 그 이유는 우리가 특징 2개만을 다루기 때문입니다. 사람 눈으로 이 식물 종들을 잘 구분할 수 있다면, 어떤 다차원 위에서는 아주 분명하게 분리된 분포들로 존재하겠죠? 하지만 그 모든 특징들을 다루기도 어렵고, 또 때로는 분포를 잘 분리해줄 수 있는 적절한 특징을 정의하는 것조차 힘든 것이 현실입니다. 실제로는 위와 같이 명확하게 정의할 수 있는 허접한 특징들 몇 가지만을 사용할 수 밖에 없는데, 분포가 제대로 분리가 되지 않는 경우가 흔합니다. 제가 임의로 가정한 상황이긴 하지만, 저 정도의 분리도라면 아마 아주 양호한 편일 겁니다. 아무튼 K를 바꿔가면서 레이블 분류 경계가 어떻게 바뀌는지 관찰해 봅시다.

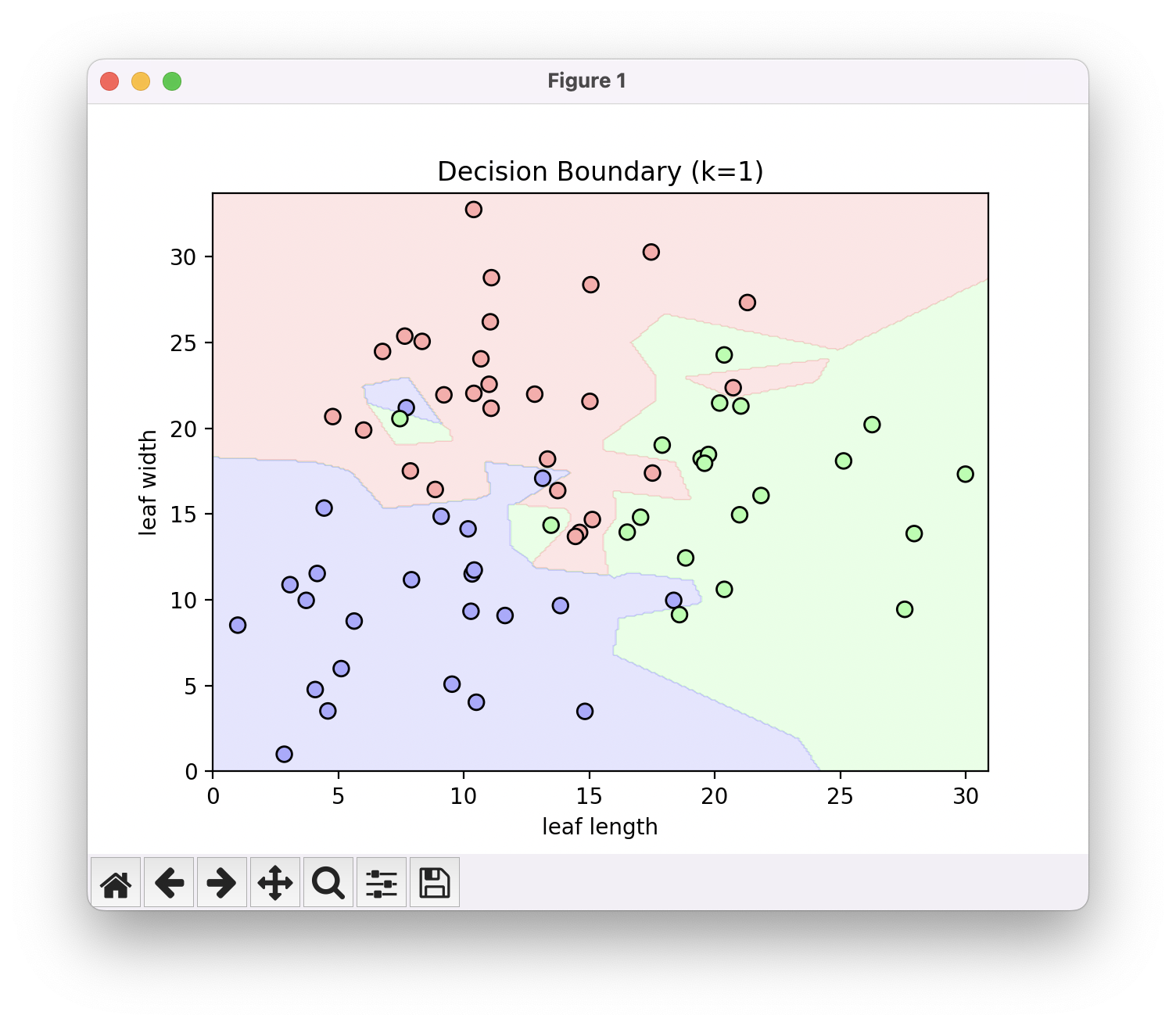
image-20250721020333719

K가 1일 때..

image-20250721020447413

K가 3일 때..

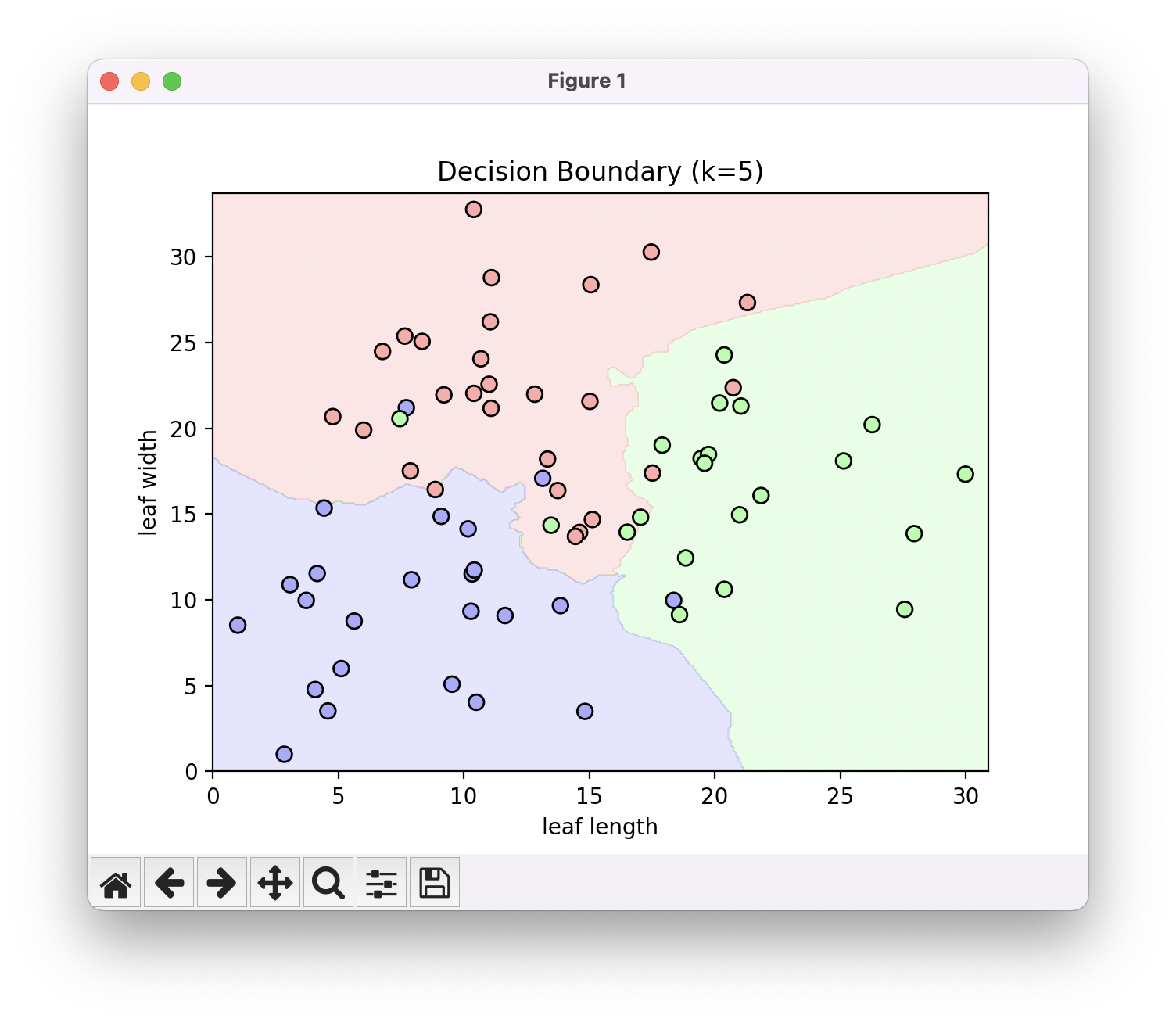
image-20250721020456938

K가 5일 때..

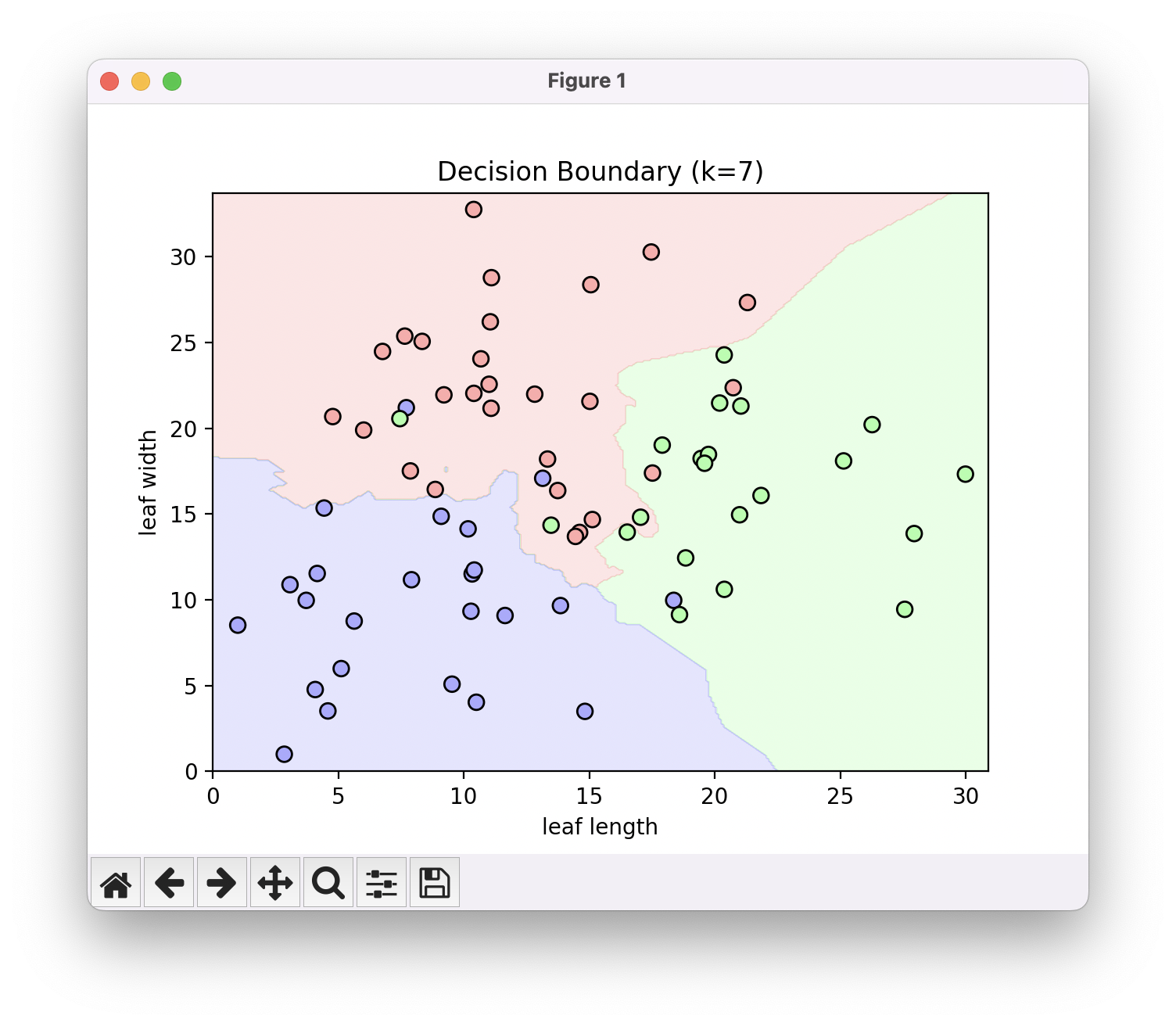
image-20250721020505998

K가 7일 때 모습입니다.

어째 조금씩 경계가 부드러워지는 경향성을 확인할 수 있습니다. 경계가 이리저리 들쭉날쭉 한 것 보다는 각 레이블에 해당하는 점들의 중심 기준으로 부드러운 경계가 그려진 모습이 우리의 직관과 더 맞는 ‘올바른 경계‘일 것입니다.

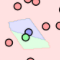
image-20250811013745349

예시로 K가 1일 때, 빨간색 점들의 영역 한가운데에 보라색과 초록색 레이블 영역이 외딴 섬처럼 존재하는 것을 확인할 수 있습니다. 그렇다면 과연 테스트 데이터를 분류할 때 저 영역에 속하는 데이터를 보라색, 또는 초록색으로 분류하는게 맞을까요? 그렇게 하는 것 보다는 주위가 빨간색이고 하니, 훈련 데이터에 좀 이상한 친구가 들어왔구나~ 하고 빨간색으로 분류하는게 합리적이겠죠? 이렇듯 KNN 알고리즘에서 K값이 너무 작으면 훈련 데이터에 지나치게 매몰되는 좋지 않은 결과에 빠지게 됩니다.

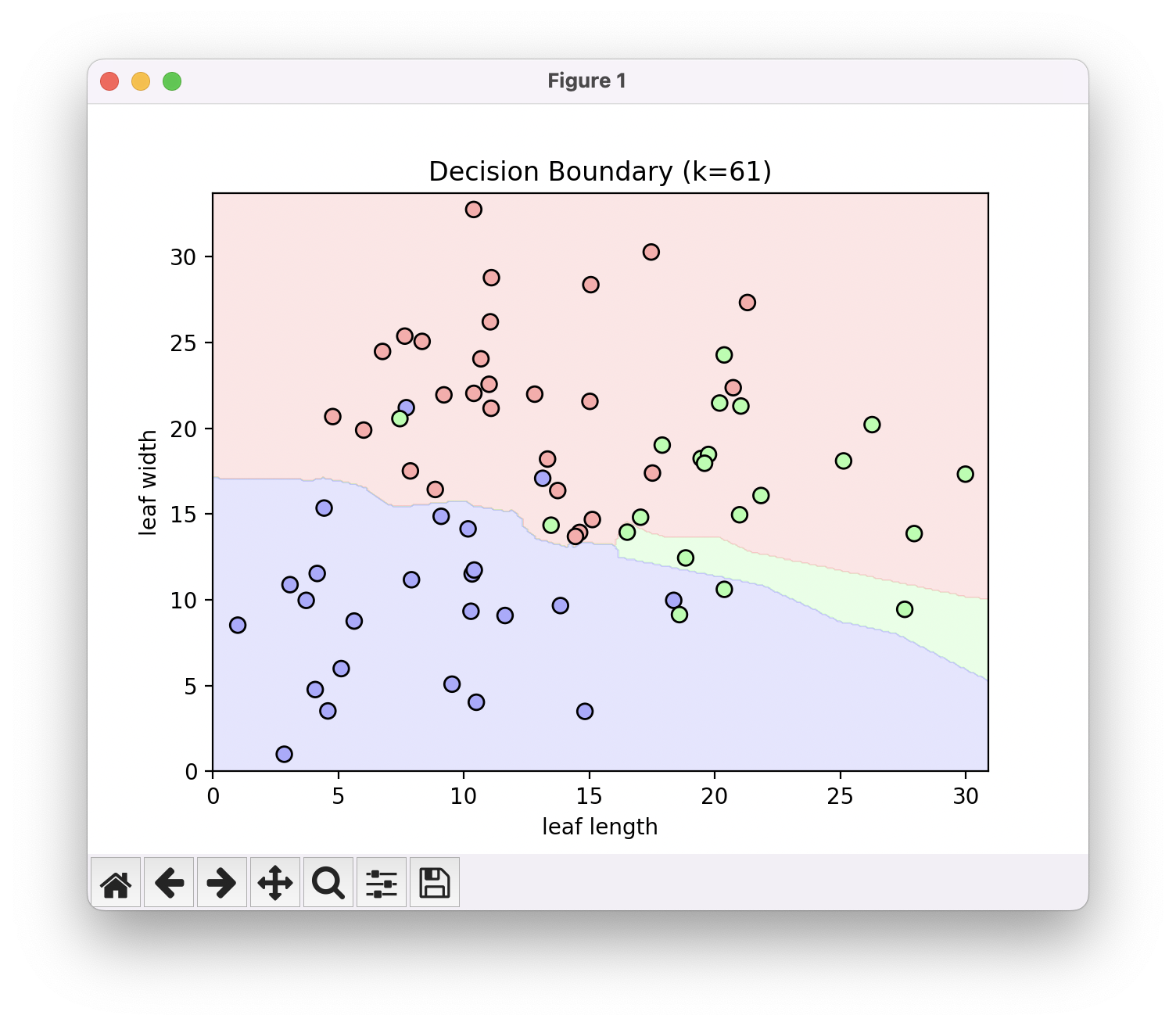
image-20250721021104687

그렇다고 K값이 무조건 크다고 좋은 것은 아닙니다. K값이 계속 커지다 보면 위와 같이 데이터의 분포를 정확하게 해석하지 못하게 됩니다. 따라서 학습 데이터로부터 올바른 경계를 뽑아낼 수 있도록 적당한 K값을 결정하는게 KNN 알고리즘에서 가장 중요한 부분입니다.

이렇게 알고리즘에서 우리가 직접 정해줘야하는 상수를 하이퍼파라미터(Hyperparameter)라고 부릅니다. 이 하이퍼파라미터는 모집단을 대표하는 테스트 데이터를 적절히 분류하도록 설정되어야 하지만, 테스트 데이터를 보고 결정해서는 안됩니다. 훈련 데이터와 테스트 데이터를 따로 두는 이유가 테스트 데이터를 모집단의 대표로 사용하고 싶어서거든요. 그러니까 이 테스트 데이터에서 이 정도의 정확도로 분류를 한다면, 우리가 수집하지 않은 모집단의 다른 데이터들도 비슷한 정확도로 분류를 하겠구나~ 하고 생각하겠다는 얘기입니다. 그런데 만약에 우리가 수집해놓은 테스트 데이터들을 최적으로 분류할 수 있는 맞춤 하이퍼파라미터를 찾아나서게 되면, 당연히 그 테스트 데이터들의 분류 정확도는 높아지겠죠. 하지만 그 맞춤 하이퍼파라미터가 우리가 수집하지 않은 모집단의 데이터들에 대해서도 비슷한 정확도를 내주는지는 모르는 일이 되어버립니다. 다시 말해 그 테스트 데이터들이 모집단을 대표할 수 있는 기능이 상실되는것이죠.

요런 문제점을 해결하기 위해서 학습 데이터 모두를 사용하지 않고, 그 중 일부를 하이퍼라미터를 결정하기 위한 Validation Set으로 따로 떼어놓는 전략을 사용합니다.

image-20250721024429768

Training Set은 모델을 학습시킬 때 사용하고 Validation Set을 가장 잘 설명할 수 있는 값으로 하이퍼파라미터를 설정합니다. 이후 Test Set으로 모델의 정확한 성능을 평가합니다. 우리가 학습 데이터셋을 Training Set 이랑 Validation Set으로 나눠서 이미 하이퍼파라미터까지 모델을 완전히 다 결정한 상황이고, 그 다음에 모집단에서 편향되지 않도록 랜덤 추출하여 Test Set을 구성하고 평가를 하게 되는 거니까 Test Set이 모집단을 대표하게 됩니다.

다시 돌아와서 KNN 알고리즘은 정말 단순하고도 강력한 도구인데요, 아쉽게도 이미지를 분류할 때 사용하기는 어렵습니다. 첫 번째로 KNN 알고리즘은 학습 데이터를 저장하고 있어야 합니다. 학습 데이터 편향을 낮추려면 가능한 많은 데이터를 가지고 있어야 하는데, 이 자체가 큰 부담이 됩니다. 그리고 거리를 측정할 때가 특히 문제인데, 사람이야 좌표평면을 딱 보고 가까운 학습 데이터들을 바로 파악할 수 있지만, 컴퓨터는 모든 학습 데이터들과 거리를 측정해 본 후에야 가장 가까운 학습 데이터들을 알 수 있기 때문에 학습데이터가 많아지면 많아질수록 알고리즘의 수행시간이 늘어나게 됩니다.

두 번째는 차원의 저주(Curse of Dimensionality)입니다. 이미지 데이터에서는 픽셀 하나하나가 특징이 되고, 각 특징이 한 개의 차원이 되기 때문에 가로 세로 28픽셀의 흑백 이미지 데이터도 784라는 무시무시한 차원을 가지게 됩니다. 그런데 데이터 존재하는 차원의 커지면 커질수록 그 공간에 존재하는 데이터들 사이의 거리가 다 비슷비슷해지게 현상이 있는데, 이를 차원의 저주라고 부릅니다. 가까운 데이터를 보고 레이블을 분류하는게 이 알고리즘의 핵심인데, 모든 데이터들 사이의 거리가 비슷비슷해지면 당연히 알고리즘이 잘 동작하지 않게 되겠죠.

Linear Classification

또 다른 대표적인 데이터 기반 접근 방식으로 선형 분류(Linear Classification)가 있습니다.

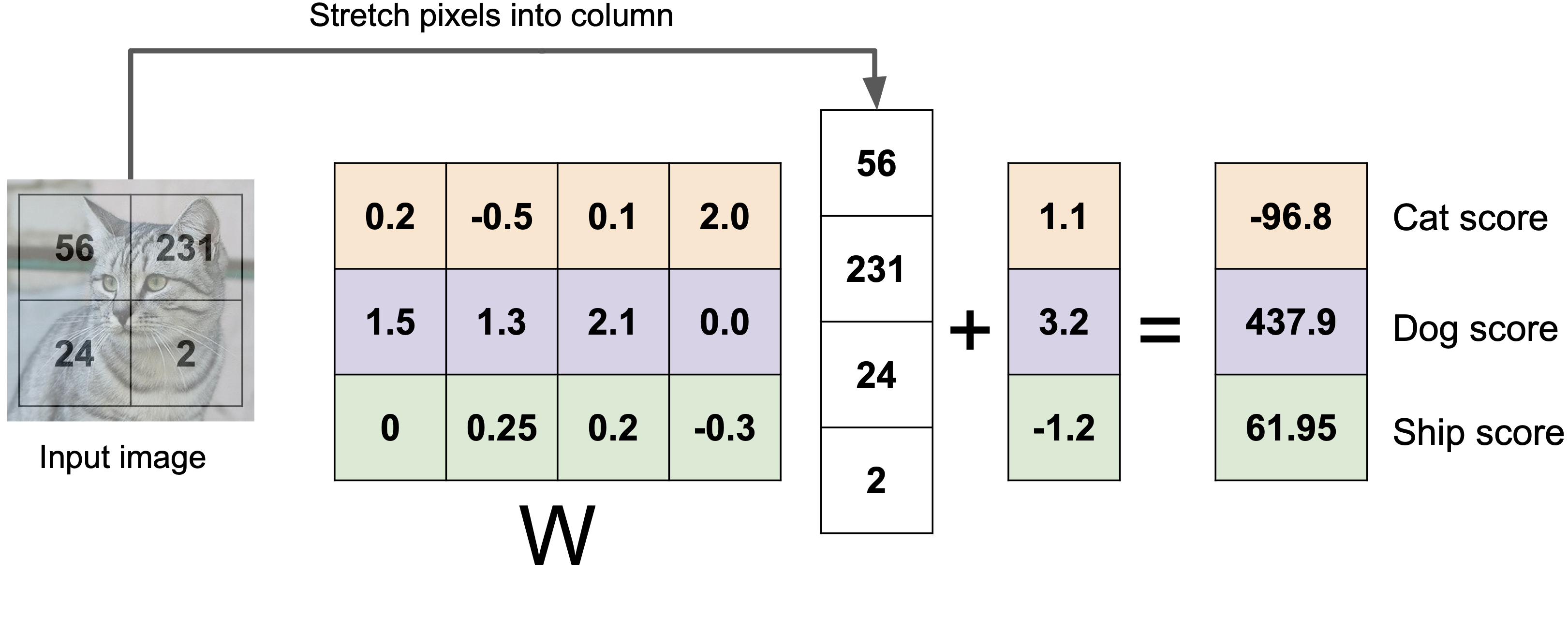
image-20250721103953578

예시로 4 픽셀짜리 사진을 분류하는 상황을 생각해봅시다. 위와 같이 2 by 2로 나타난 고양이 사진을 일렬로 펴 [56, 231, 24, 2] 라는 벡터로 표현할 수 있습니다. 이 벡터에 가중치 행렬($W$)을 곱해 3차원으로 선형변환을 해준 다음 3차원 편향 벡터($b$)를 더해줍니다. 마지막 결과 벡터에서 가장 큰 값을 가지고 있는 인덱스를 해당 이미지의 레이블로 결정합니다.

그러니까 가장 마지막 결과로 얻는 벡터에서 정답인 인덱스의 점수가 가장 크도록 만들어주는 좋은 가중치 행렬과 편향 벡터를 찾아야 합니다.

Q. 가중치 행렬($W$)과 편향 벡터($b$)는 사용자가 임의로 설정하는 값인가요?

아니요. 가중치 행렬과 편향 벡터는 사용자가 임의로 설정하는 값이 아닙니다. 데이터를 잘 분류해주기 위해 가중치 행렬($W$)과 편향 벡터($b$)에 들어가야하는 값은 방정식에 해가 있듯 이미 정해져 있는 값입니다(우리가 알지는 못하지만). 그걸 찾아야 하는데 모든 값을 다 시도해볼 수는 없어서 나중에 다른 훌륭한 알고리즘을 통해서 효율적으로 값을 찾게 되는데요, 그 방식이 처음에는 아무 숫자로 정해놓고 조금씩 조금씩 좋은 값이 될 수 있도록 바꾸는.. 그런 방식입니다. 따라서 처음에 아무 숫자로 정할 때, 그 값을 사용자가 임의로 정할 수는 있겠죠. 하지만 결국에는 알고리즘을 통해 가장 알맞은 값으로 점점 맞춰지게 됩니다. 이를 ‘학습’ 이라고 부르고, 학습 과정에서 주어진 데이터를 잘 분류할 수 있도록 조정되는 변수를 파라미터(Parameter)라고 합니다.

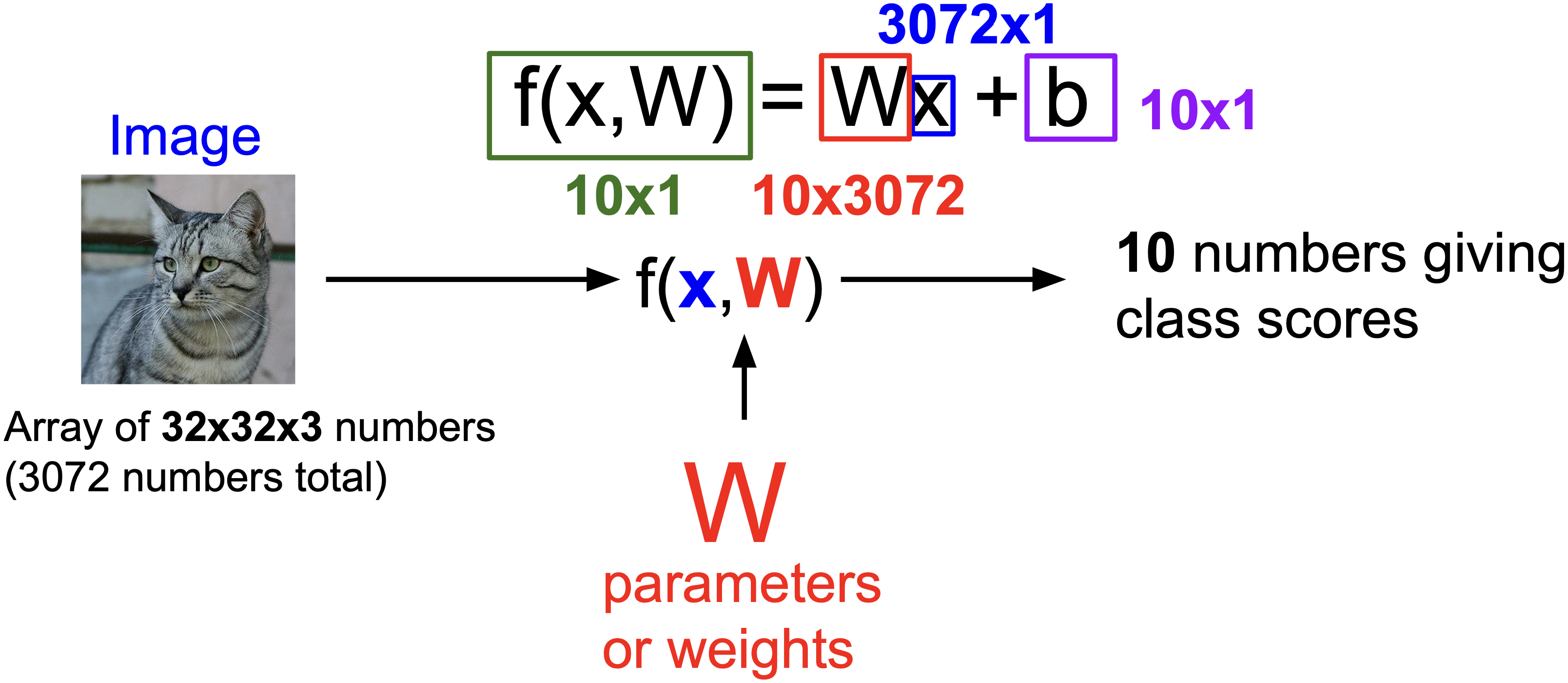
image-20250721105544794

이 모든 과정들을 좀 더 간단히 위와 같이 표현할 수 있는 거구요, 레이블의 개수가 더 많을 때에도 몇 차원으로 선형 변환 시키느냐만 다를 뿐 나머지 부분들은 동일합니다.

linear_trans

기하학적으로 보면, 위와 같은 방식으로 공간을 쭉쭉 늘린 다음, 선을 딱 그어서(고차원인 경우 초평면을 그어서) 한 쪽은 개 레이블이고, 다른 쪽인 고양이 레이블입니다~ 하고 분류하는 겁니다. 여기서 문제가 있는데..

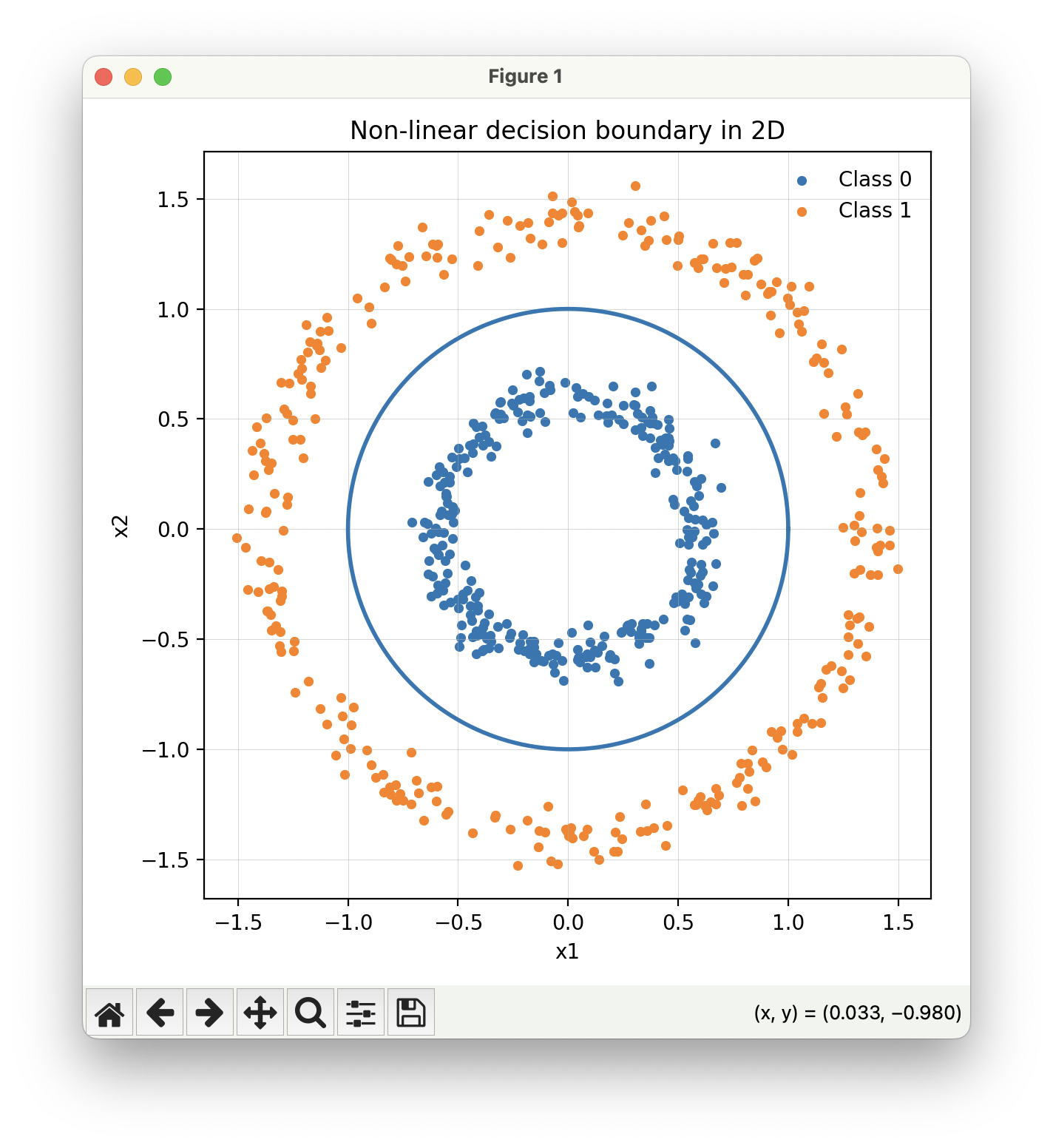
image-20250810221614586

기하학적으로는 선형변환이 방금 전의 짤에서 나타난 것과 같이 공간을 늘리거나 줄이거나 회전시키는 연산에 해당하는데, 공간을 곡선으로 휘게할 수는 없거든요. 만약에 위와 같이 원 안쪽이 하나의 레이블이고 바깥이 다른 레이블인 분포가 있다면, 공간을 아무리 늘리고 줄이고 돌리고 지지고 볶아서 공간을 변형시켜도, 그 다음에 선 하나를 딱 그어서 두 레이블을 분리해낼 수가 없습니다(다음 포스팅에서 해결합니다).

또, 가장 적절한 $W$와 $b$값을 찾아야하는데 이것도 만만치 않은 일입니다. 고양이 사진을 4픽셀로 단순화시킨 상황에서도 15개의 값들의 조합 중 최적의 조합, 그러니까 15차원 공간에서 가장 좋은 지점을 딱 찾아내야한다는 것인데 이것조차도 너무 어려운 일이구요, 단순화시키지 않은 상황에서는 사막에서 바늘 찾는 일 따위는 비교도 할 수 없을 만큼 훨씬 더 어려운 일이 됩니다. 그런데 이걸 찾게 해주는 아주 멋진 방법을 바로 이어서 다룹니다.

Loss Function

가장 적절한 $W$와 $b$값을 찾는 방법에 대해서 알아봅시다.

image-20250721132433712

고양이 사진에 대해서 고양이 레이블 점수가 3.2, 자동차 레이블 점수가 5.1으로 고양이 사진을 보고 자동차 사진이라고 분류해놨습니다.. 자동차 사진은 올바르게 분류하긴 했는데요, 개구리 사진은 또 개구리 레이블 점수가 가장 낮네요.

아무튼 완전 엉터리로 분류기가 돌아가고 있는데, 일단 분류기의 성능을 높이기 위해서는 분류기가 얼마만큼 잘하는지를 정량적으로 평가할 수 있어야 합니다. 다시 말해, 현재 분류기(구체적으로는 분류기를 구성하는 $W$와 $b$)의 불량도를 정량적으로 측정하는 함수가 필요한데, 이를 손실 함수(Loss Function)라고 부릅니다.

손실 함수를 선정해 분류기의 불량도를 정량적으로 측정한 다음에는 이 값을 이정표삼아 $W$와 $b$의 모든 공간에서 가장 좋은 조합을 효율적인 절차를 통해 찾아야 합니다(주먹구구식으로 모든 공간을 싹 다 탐색하기에는 너무 넓기 때문이죠). 이를 최적화(Optimization)이라고 부르고 문서 후반에 그 내용을 다룹니다.

\[\{(x_i, y_i)\}^{N}_{i=1}\]

분류기의 잘하고 못한 정도를 판단하기 위해서는 먼저 데이터셋이 필요합니다. 실제로 고양이 사진을 넣어보고, 차 사진을 넣어봐야 이 분류기가 얼만큼 잘 동작하는지 알 수 있죠. 위의 데이터셋에서 $x_i$는 이미지, $y_i$는 이미지에 대응되는 정답 레이블(고양이 사진이면 ‘고양이’, 강아지 사진이면 ‘강아지’)입니다.

\[s = f(x_i, W) = [s_0, s_1, ...]\]

위에서 $W$는 일반적으로 모델에서 사용되는 모든 파라미터(가중치 벡터와 편향치)를 대표합니다. 위의 고양이 사진이 데이터셋의 $i$번째 데이터일 때, 이 $i$번째 사진을 넣은 결과물로 [3.2, 5.1, -1.7]의 벡터를 얻을 수 있었습니다. 이게 $f(x_i, W)$에 해당되고 이것을 스코어 벡터(Score Vector)라고 부릅니다.

\[L_i(f(x_i, W), y_i)\]

다음으로, 분류기가 출력한 결과가 실제 정답과 비교했을 때 얼마나 잘하는지를 정량적으로 평가합니다. 이 과정으로 데이터셋의 모든 이미지들의 손실 값을 구한 다음 다 더하고 데이터 개수로 나눠 최종적인 평균 손실 값을 구합니다.

\[L = \frac{1}{N}L_i(f(x_i, W), y_i)\]

손실 값을 구하는 절차를 알아봤고, 이제 구체적인 손실 함수가 어떻게 생겨먹은 친구인지 알아봅니다.

SVM(Soft Vector Machine) Loss

\(L_i = \sum_{j \neq y_i}\max(0, s_j - s_{y_i} + 1)\) 위 수식은 다분류 문제에서 사용할 수 있도록 일반화된 SVM Loss입니다.

image-20250721141238094

$0$과 $s_j - s_{y_i} + 1$ 중 큰 값을 선택하기 때문에 $s_j - s_{y_i} + 1$이 $0$보다 작아지기 전까지는 손실이 존재합니다. $s_j - s_{y_i} + 1$는 $s_j$(정답이 아닌 레이블의 스코어)$ + 1$와 $s_{y_i}$(정답 레이블의 스코어) 사이의 차이라고 해석할 수 있으니까, 정답 레이블의 스코어가 정답이 아닌 모든 레이블의 스코어보다 1 이상 차이가 존재할 때(더 클 때) 손실이 발생하지 않는다, 다시 말하면 이 손실함수는 정답 레이블의 스코어가 정답이 아닌 레이블의 스코어보다 최소 1만큼은 크기를 바란다고 이해할 수 있습니다.

Regularization

손실 함수를 사용해 각 W가 특정 데이터셋을 설명하는데에 있어 얼마만큼의 불량도를 가지는지 측정할 수 있게 됐습니다. 만약 특정 학습 데이터셋에 대한 손실 값이 $0$인 $W$가 있다면 그 W는 유일한 손실 값이 0이 되게 하는 유일한 $W$일까요? 정답은 그렇지 않다 입니다. 그 간단한 예시로 $W$의 2배인 $2W$가 있는데요, 계산 해 볼 것 도 없이 당연히 손실 값이 $0$입니다. 그 3배도 $0$, 4배도 $0$… 결국 손실 값이 $0$이 되도록 하는 $W$는 무한히 많이 존재합니다. 만약 그렇다면 그 많은 $W$ 중 어떤 $W$를 선택해야 할까요? 손실값이 낮게 나온다고 무조건 좋은 $W$가 맞긴 한 걸까요?

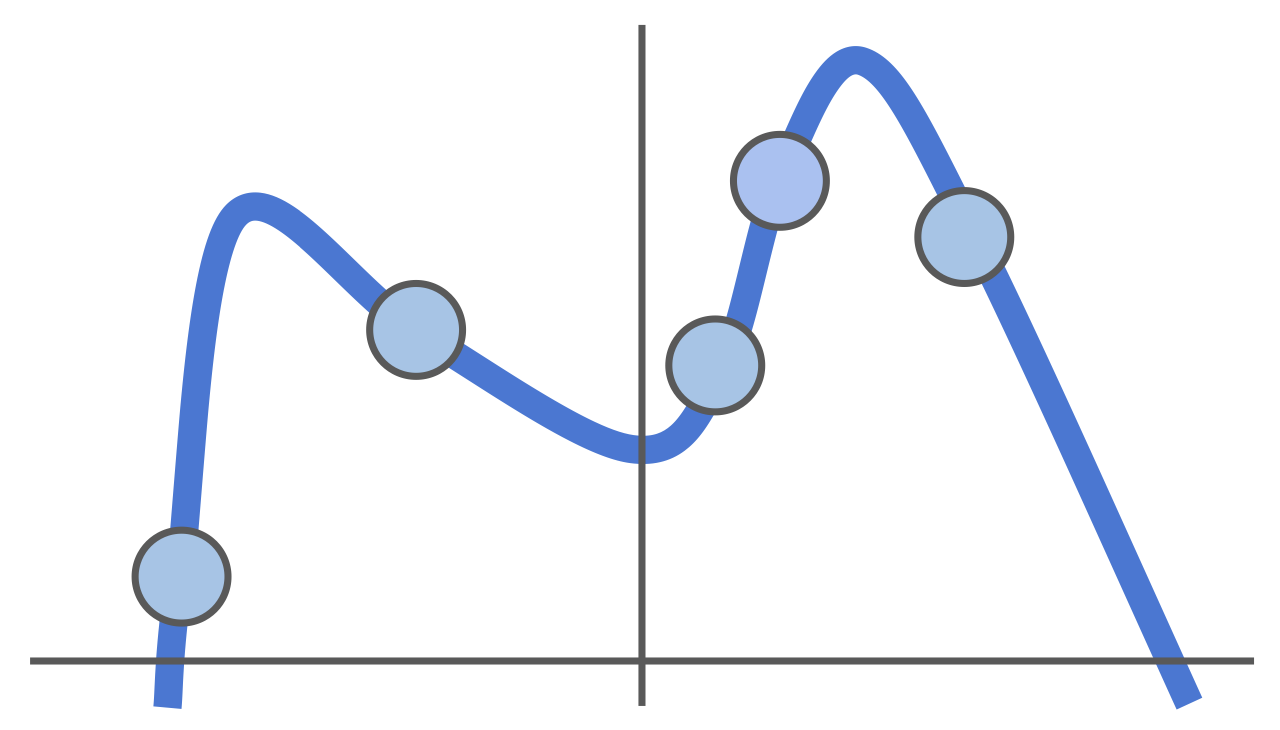
image-20250721144222171

잠시 분류 문제에서 벗어나 좀 더 일반적인 머신러닝 개념을 살펴봅니다. 위와 같은 5개의 훈련 데이터를 설명하는 모델은 수도 없이 많습니다. 하지만 위 예시의 모든 훈련 데이터의 손실 값이 0이 되도록 만들려면 모델은 최소 4차 다항식의 꼴을 갖춰야 합니다. 그래서 손실 값을 최소화하기 위해 4차 다항식으로 모델을 설정했습니다. 그런데요..

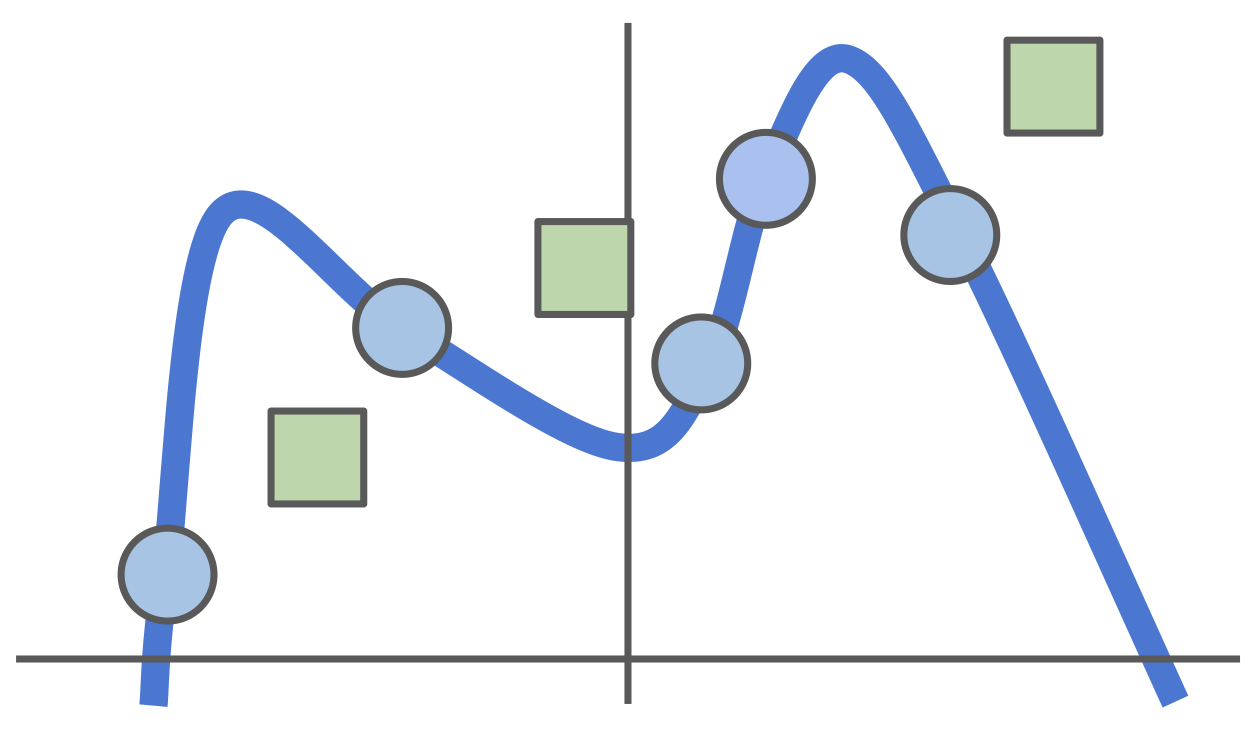
image-20250721144851568

실제로 테스트 데이터를 넣어보니 모델이 테스트 데이터를 전혀 설명하지 못합니다. 위의 모든 데이터들을 놓고 다시 보니 4차 다항식으로 설정할 것이 아니라 선형 모델을 사용했을 때 훨씬 테스트 데이터를 잘 설명할 수 있었을 것 같아 보이죠. 이처럼 훈련 데이터의 손실 값을 줄이는 데에 지나치게 매몰되면 오히려 테스트 데이터를 잘 설명하지 못하는 현상이 발생하는데 이를 과적합(Overfitting)이라고 합니다.우리 세상의 다양한 문제들은 가능한 단순한 모델로 설명할 때에 모집단이 더 잘 설명되는 경향이 있습니다(오캄의 면도날이라고도 부르는..). 따라서 모델이 너무 복잡한 형태를 띄지 않도록 제한할 필요가 있습니다. 이를 Regularization이라고 합니다.

\[L = \frac{1}{N}L_i(f(x_i, W), y_i) + \lambda R(W)\] \[R_{L_1}(W) = \sum |W|\] \[R_{L_2}(W) = \sum W^2\]

Regularization은 손실함수에 모델의 복잡도를 대표하는 텀을 추가하는 방식을 통해 반영됩니다. 그러니까 모델의 복잡도가 높으면 전체 손실함수의 값도 커지는 구조를 갖게 되죠. 크게는 L1(LASSO) Regularization과 L2(Ridge) Regularization이 있습니다. L1 Regularization은 모델의 모든 파라미터의 절댓값을 더한 값을 모델의 복잡도로 사용하고 L2 Regularization은 모델의 모든 파라미터의 제곱값을 더한 값을 모델의 복잡도로 사용합니다. 만약 우리가 n차 다항식의 각 계수를 파라미터로 결정해야 하는 상황이라면, 모든 훈련 데이터의 손실 값을 0으로 맞추기 위해 고차 계수항을 설정하는 것보다 어느 정도 훈련 데이터 손실 값을 감수하더라도 고차 계수항을 0으로 버리고 모델을 단순화하는게 전체 손실 값 측면에서는 더 낮은 값에 도달하게 만듭니다.

Multinomial Logistic Regression

Multinomial Logistic Regression은 Score를 좀 더 다른 방식으로 사용합니다. SVM에서는 Score가 각 레이블의 점수에 불과하고 그 점수가 단순히 다른 레이블 점수보다 크면 될 뿐, 이게 구체적으로 무엇을 의미하는 지에는 크게 관심이 없었습니다. 그런데 Multinomial Logistic Regression에서는 Score를 정규화시켜 모든 레이블이 가지는 값의 합이 1이 되도록 만들어줍니다. 그리고 이것을 ‘모델이 판단하기에 이 데이터가 각 해당 레이블에 속할 확률‘이라고 해석합니다.

\[P(Y=k | X = x_i) = \frac{e^sk}{\sum_j{e^{s_j}}}\]

위의 식과 같이 각 레이블의 스코어에 Exponential을 취한 다음 합이 1이 되도록 정규화하는 과정의 식을 Softmax라고 부릅니다.

image-20250721160503677

아까 위에서 다룬 고양이 사진 예시입니다. 고양이 레이블 점수가 3.2, 자동차 레이블 점수가 5.1, 그리고 개구리 점수가 -1.7인데요, 이거를 Softmax를 통해 스코어를 정규화시킨 다음에는, 고양이 레이블에 속할 확률이 13%, 자동차 레이블에 속할 확률이 87%, 그리고 개구리 레이블에 속할 확률이 0%(실제로는 아주 작은 확률은 존재합니다)라는 식으로 해석하게 됩니다.

자 이렇게 스코어를 확률으로 해석하기로 했는데, 모델이 각 레이블에 속할 확률이라고 생각한것이 실제로 얼마나 맞는지를 통해 정량적으로 평가해야겠죠? 위 상황에서는 실제 고양히 사진인것을 고양이 레이블에 속할 확률이 13%라고 했으니 꽤나 큰 손실을 받아야 겠네요. 그 값은 정답 레이블의 확률(위의 예시에서는 0.13)에 음의 로그를 취하는 Cross Entropy Loss(CE Loss)를 통해 구해집니다.

\[\text{CE Loss} = -\log(\frac{e^sk}{\sum_j{e^{s_j}}})\]

스코어를 확률로 변형시키는 것부터, 이 때 사용하게 되는 CE Loss까지 살펴봤는데, 왜 이런 다른 방식을 사용하는 건지, 구체적으로 Cross Entropy Loss와 SVM Loss이 어떻게 다른 것인지 살펴봅시다.

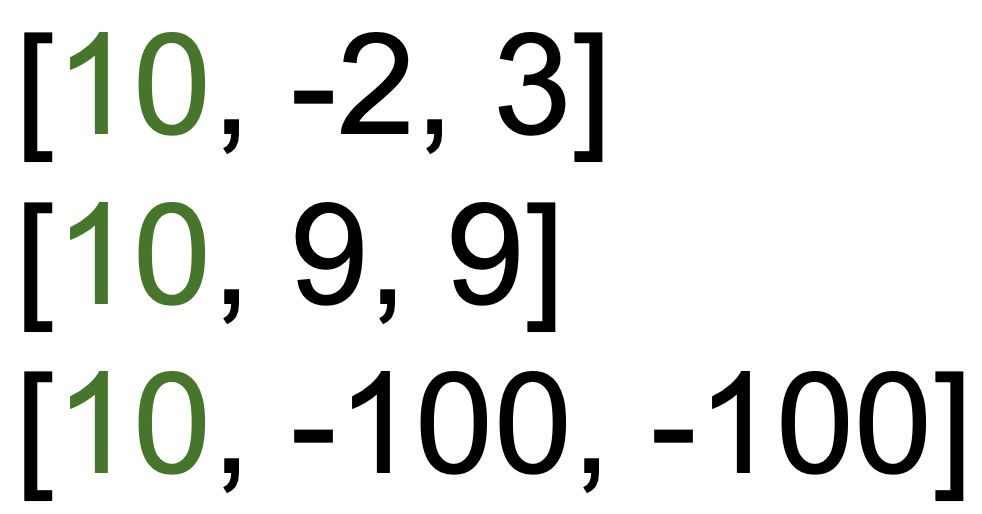
image-20250721160930497

위 예시에서 초록색 글자에 해당하는 0번째 레이블이 정답 레이블일 때, SVM Loss의 손실 값은 0입니다. SVM Loss은 정답 스코어가 정답이 아닌 스코어보다 마진 만큼만(대부분의 경우에 1로 설정) 크도록 이끌기 때문에, 위의 상황에서 더 이상 손실 값이 발생하지 않습니다. 반면, Cross Entropy Loss의 경우 정답 레이블의 확률 값이 1이 될 때까지 손실 값이 발생합니다. SVM과 비교했을 때 지속적으로 개선하려고 노력하다는 차이점이 있습니다(실제 어플리케이션에서는 큰 차이가 있지는 않지만 차이점은 알고 있어야 합니다).

Optimization

CE Loss이든, SVM Loss이든, 분류기의 파라미터를 평가할 수 있게 됐으니 이제는 가장 최선의 분류기를 찾아 나설 차례입니다. 가장 쉽게 떠오르는 방법은 랜덤 탐색입니다. 파라미터 공간에서 랜덤한 조합을 찍고 손실 함수를 계산해 본 다음, 이전에 가지고 있던 파라미터 보다 더 낫다고 판단되면 새로운 파라미터로 채택하는 방법이죠. 위의 간단한 예시에서조차 15차원 실수 차원에서 탐색해야 했는데, 억 단위를 우습게 넘는 최신 모델에서는 당연히 적용가능한 방법이 아니겠죠.

image-20250721162456638

또 다른 아이디어로는 경사를 따라 내려가는 방법이 있습니다. 산 중턱 어딘가에 서 있을 때 눈을 감고 발바닥이 느끼는 기울기만으로도 산 아래까지 내려갈 수 있듯이, 현재 파라미터에서 손실 값이 가장 가파르게 줄어드는 방향(기울기)을 계산한 뒤 그 방향으로 파라미터를 조금씩 조정해 나가는 방법을 경사 하강법(Gradient Descent)이라고 부릅니다.

\[L = \frac{1}{N}L_i(f(x_i, W), y_i) + \lambda R(W)\] \[\frac{\partial L}{\partial W}\]

$W$를 통해 $L$(손실)까지 구하는 식이 우리에게 주어져 있기 때문에 위 식을 각 파리미터에 대해 편미분해서 손실의 기울기($\frac{\partial L}{\partial W}$)를 구할 수 있습니다. 물론 그 과정이 조금 어려울 수는 있지만… 어쨌든 핵심은 구할 수 있다는 것이고, 그 기울기를 사용해 $W$를 살살 움직이다 보면 손실 값이 최소인 지점에 도달할 수 있습니다.

모델을 학습할 때는 대개 훈련 데이터셋의 용량이 매우 큽니다. 전통적인 배치(Batch) 학습 방법에서는 손실 함수를 계산할 때 전체 데이터셋에 대한 각 샘플 손실의 평균을 구해야 하는데, 여기서 배치란 한 번에 모델이 학습에 사용하는 데이터 전체를 의미합니다. 즉, 배치 크기가 곧 전체 데이터셋 크기인 셈이어서, 한 번의 파라미터 업데이트를 위해 모든 데이터를 처리하면 시간이 너무 오래 걸립니다. 이를 해결하기 위해 사용하는 것이 미니배치(Mini-batch) 학습입니다. 미니배치는 전체 데이터 중 무작위로 추출한 소량의 샘플 집합으로, 일반적으로 수십에서 수백 개의 샘플로 구성됩니다. 매 스텝마다 이 미니배치 단위로 손실과 기울기를 계산하면, 전체 데이터셋을 다룰 때와 비교해 계산량이 크게 줄어들면서도 업데이트 방향이 크게 달라지지 않기 때문에 학습 속도가 빠르게 개선되는데요, 이를 확률적 경사 하강(Stochastic Gradient Descent)이라고 말합니다.

아무튼 편미분을 할 수 있다고 넘어갔는데, 이걸 구체적으로 어떻게 하겠다는 건지는 다음 포스팅에서 다뤄보겠습니다.

댓글남기기

참고

Isaac Sim & ROS2

3 분 소요

이 포스팅은 ‘Isaac Lab‘에 대한 내용을 담고 있습니다.